Engage NY Eureka Math Precalculus Module 2 Lesson 20 Answer Key
Eureka Math Precalculus Module 2 Lesson 20 Exploratory Challenge Answer Key
Exploratory Challenge
For this Exploratory Challenge, we consider an arch made with five trapezoidal stones on top of the base columns as shown. We focus only on the stones labeled 1, 2, and 3.
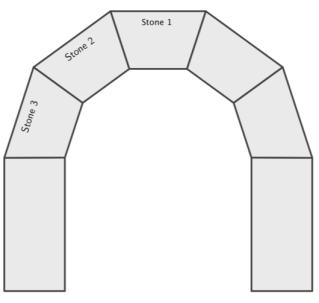
a. Study the force vectors acting on the keystone (stone 1) and stones 2 and 3 on the left side of the arch. Why is it acceptable for us to disregard the forces on the right side of the arch?
Answer:
Due to symmetry, the forces on the right side of the arch are the same magnitude as the forces on the left, but with directions reflected across the vertical line through the center of the keystone.
b. First, focus on the forces acting on the keystone. Stone 2 pushes on the left side of the keystone with force vector p1L. The stone to the right of the keystone pushes on the right of the keystone with force vector p1R. We know that these vectors push perpendicular to the sides of the stone, but we do not know their magnitude. All we know is that vectors p1L and p1R have the same magnitude.
i. Find the measure of the acute angle formed by p1L and the horizontal.
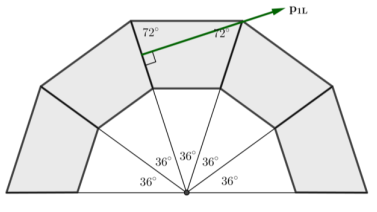
Answer:

We need to consider the angles in the triangles formed by the trapezoidal stones. Since there are five stones that form the arch, each trapezoid creates a triangle with angles that measure 36°, 72°, and 72°. The vector p1L is shown in green. Looking more closely at just the keystone, we see that the 36° angle is bisected by the vertical line through the center of the keystone. Thus, the angle p1L makes with the vertical direction is 90° + 18°. Therefore, vector p1L makes an 18° angle with the horizontal axis.
ii. Find the measure of the acute angle formed by p1R and the horizontal.
Answer:
Due to symmetry, the acute angle formed by p1R and the horizontal is congruent to the acute angle formed by p1L and the horizontal. Thus, this angle measures 18°.
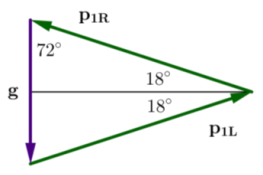
c. Move vectors p1L, p1R and g tip – to – tail. (g is the force due to gravity and should be vertical.) Why must these vectors form a triangle?
Answer:
Because the keystone does not move, we know that the forces acting on the stone sum to zero. Thus, the vectors that represent these forces will form a triangle when placed tip – to – tail, as we saw in the previous lesson.
d. Suppose that vector g has magnitude 1. Use triangle trigonometry together with the measure of the angles you found in part (b) to find the magnitudes of vectors p1L and p1R to the nearest tenth of a unit.
i. Find the magnitude and direction form of g.
Answer:
We know that g has magnitude 1 and direction –90° from the positive horizontal axis.
ii. Find the magnitude and direction form of p1L.
Answer:
Using the figure at right, we see that there are two right triangles with angles 18° and 72°. Since g has magnitude 1, these triangles have a short leg of length \(\frac{1}{2}\). We will use x to represent the magnitude of p1L. Using triangle trigonometry, we see that
sin(18°) = \(\frac{1 / 2}{x}\) and then x = \(\frac{1}{2 \sin \left(18^{\circ}\right)}\) ≈ 1.6.
Thus, vector p1L has magnitude 1.6 and direction 18° from the positive horizontal axis.
iii. Find the magnitude and direction form of p1R.
Answer:
Due to symmetry, we know that ‖p1R ‖ = ‖p1L ‖ so the magnitude of p1R is also 1.6. Then the vector p1R has magnitude 1.6 and direction 162° from the positive horizontal axis.
e. Vector p1L represents the force of stone 1 pushing on the keystone, and by Newton’s third law of motion, there is an equal and opposite reaction. Thus, there is a force of the keystone acting on stone 2 that has the same magnitude as p1L and the opposite direction. Call this vector v1L.
i. Find the magnitude and direction form of v1L.
Answer:
The vector v1L has magnitude 1.6 and direction – 162° from the positive horizontal axis.
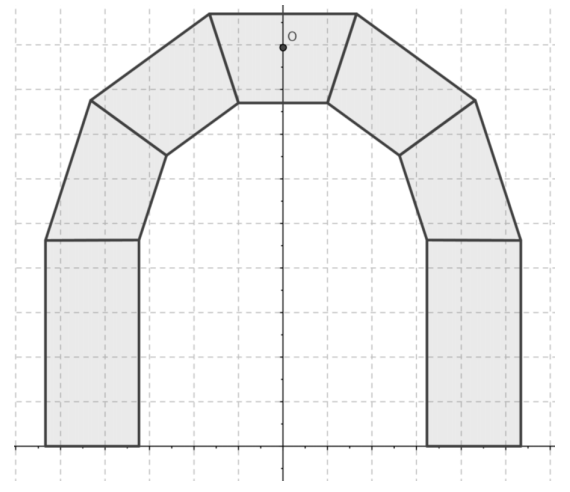
ii. Carefully draw vector v1L on the arch on the next page, with initial point at the point marked O, which is the center of mass of the keystone. Use a protractor measured in degrees and a ruler measured in centimeters.
Answer:
See the final drawing in part (i).
f. Assume that the forces v2L of stone 2 acting on stone 3 and v3L of stone 3 acting on the base column have the same magnitude as each other, and twice the magnitude as the force v1L. Why does it make sense that the force vector v1L is significantly shorter than the other two force vectors?
Answer:
The keystone compresses the stones on both the left and right sides of the arch equally, so the gravitational pull on that stone is split in half down the right and left sides. Thus, it is reasonable to assume that the stones 2 and 3 act with twice the compressive force as stone 1.
g. Find the magnitude and direction form of vector v2L, the force of stone 2 pressing on stone 3. Carefully draw vector v2L on the arch on the next page, placing its initial point at the terminal point of v1L.
Answer:
Vector v2L has twice the magnitude of vector v1L, so its magnitude is 3.2. Because each stone is rotated 36° from the neighboring stones, vector v2L is rotated – 162° + 36° = – 126° from the horizontal. Thus, vector v2L has magnitude 3.2 and direction – 126° from the positive horizontal axis.
h. Find the magnitude and direction form of vector v3L, the force of stone 3 pressing on the base column. Carefully draw vector v3L on the arch on the next page, placing its initial point at the terminal point of v2L.
Answer:
Vector v3L has the same magnitude as vector v2L and it is rotated an additional 36° counterclockwise. Thus, vector v3L has magnitude 3.2 and direction
– 126° + 36° = – 90° from the positive horizontal axis. Thus, vector v3L points straight downward.
i. Use the parallelogram method to find the sum of the force vectors v1L, v2L, and v3L on the left side of the arch.
Answer:
(The diagram of the force vectors is shown below.)

j. Will the arch stand or fall? Explain how you know.
Answer:
The forces are all contained within the arch, so the arch will stand.
Plot the force vectors acting on the arch on this diagram to determine whether or not this arch is able to stand or if it collapses.
Eureka Math Precalculus Module 2 Lesson 20 Problem Set Answer Key
Question 1.
Vectors v and w are given in magnitude and direction form. Find the coordinate representation of the sum v + w and the difference v – w. Give coordinates to the nearest tenth of a unit.
a. v: magnitude 12, direction 50° east of north
w: magnitude 8, direction 30° north of east
Answer:
v = 〈12 cos(40°), 12 sin(40°) 〉; w = 〈8 cos(30°), 8 sin(30°) 〉
v + w ≈ 〈16.1, 11.7〉
v – w ≈ 2.3, 3.7〉
b. v: magnitude 20, direction 54° south of east
w: magnitude 30, direction 18° west of south
Answer:
v = 〈20 cos( – 54°), 20 sin( – 54°) 〉; w = 〈30 cos( – 108°), 30 sin( – 108°) 〉
v + w ≈ 〈2.5, – 44.7〉
v – w ≈ 〈21.0, 12.4〉
Question 2.
Vectors v and w are given by specifying the length r and the amount of rotation from the positive x – axis. Find the coordinate representation of the sum v + w and the difference v – w. Give coordinates to the nearest tenth of a unit.
a. v: length r = 3, rotated 12° from the positive x – axis
w: length r = 4, rotated 18° from the positive x – axis
Answer:
v = 〈3 cos(12°), 3 sin(12°) 〉; w = 〈4 cos(18°), 4 sin(18°) 〉
v + w ≈ 〈6.7, 1.9〉
v – w ≈ 〈 – 0.9, – 0.6〉
b. v: length r = 16, rotated 162° from the positive x – axis
w: length r = 44, rotated – 18° from the positive x – axis
Answer:
v = 〈16 cos(162°), 16 sin(162°) 〉; w = 〈44 cos( – 18°), 44 sin( – 18°) 〉
v + w ≈ 〈26.6, – 8.7〉
v – w ≈ 〈 – 57.1, 18.5〉
Question 3.
Vectors v and w are given in magnitude and direction form. Find the magnitude and direction of the sum v + w and the difference v – w. Give the magnitude to the nearest tenth of a unit and the direction to the nearest tenth of a degree.
a. v: magnitude 20, direction 45° north of east
w: magnitude 8, direction 45° west of north
Answer:
The tip of the vector v has coordinates (10\(\sqrt{2}\), 10\(\sqrt{2}\)) and tip of vector w has coordinates ( – 4\(\sqrt{2}\), 4\(\sqrt{2}\)). Then the sum has tip v + w = (6\(\sqrt{2}\), 14\(\sqrt{2}\)). The rotation of v + w is θ = arctan\(\left(\frac{14 \sqrt{2}}{6 \sqrt{2}}\right)\) = arctan \(\left(\frac{7}{3}\right)\), so θ ≈ 66.8°. The length of v + w is |v + w| = \(\sqrt{(6 \sqrt{2})^{2} + (14 \sqrt{2})^{2}}\) = \(\sqrt{464}\) ≈ 21.5. Thus, v + w has magnitude approximately 21.5
and direction 66.8° north of east.
The difference has tip v – w = (14\(\sqrt{2}\), 6\(\sqrt{2}\)). The rotation of v – w is θ = arctan \(\left(\frac{6 \sqrt{2}}{14 \sqrt{2}}\right)\) = arctan \(\left(\frac{3}{7}\right)\), so θ ≈ 23.2°. The length of v – w is |v – w| = \(\sqrt{(14 \sqrt{2})^{2} + (6 \sqrt{2})^{2}}\) = \(\sqrt{464}\) ≈ 21.5. Thus, v – w has magnitude approximately 21.5 and direction 23.2° north of east.
b. v: magnitude 12.4, direction 54° south of west
w: magnitude 16.0, direction 36° west of south
Answer:
Since 54° south of west and 36° west of south are the same direction, vectors v and w are collinear. Thus, the vector v + w has length 12.4 + 16 = 28.4 and direction 54° south of west.

The vector v – w has length |12.4 – 16| = 3.6 and direction 54° north of east.
Question 4.
Vectors v and w are given by specifying the length r and the amount of rotation from the positive x – axis. Find the length and direction of the sum v + w and the difference v – w. Give the magnitude to the nearest tenth of a unit and the direction to the nearest tenth of a degree.
a. v: magnitude r = 1, rotated 102° from the positive x – axis
w: magnitude r = \(\frac{1}{2}\), rotated 18° from the positive x – axis
v = 〈cos(102°), sin(102°) 〉; w = 〈\(\frac{1}{2}\) cos(18°), \(\frac{1}{2}\) sin(18°) 〉
v + w ≈ 〈0.3, 1.1〉
‖v + w‖ ≈ \(\sqrt{0.3^{2} + 1.1^{2}}\) ≈ 1.2
arctan \(\left(\frac{1.1}{0.3}\right)\) ≈ 74.7°
The sum v + w has magnitude approximately 1.2 and direction 74.7° from the positive x – axis.
v – w ≈ 〈 – 0.7, 0.8〉
‖v – w ‖ ≈ \(\sqrt{0.7^{2} + 0.8^{2}}\) ≈ 1.1
arctan \(\left( – \frac{0.8}{0.7}\right)\) ≈ – 48.8°
Since v – w lies in the second quadrant, it aligns with the terminal ray of rotation by
180° – 48.8° = 131.2°. The vector v – w has magnitude approximately 1.1 and direction 131.2° from the positive x – axis.
b. v: magnitude r = 1000, rotated – 126° from the positive x – axis
w: magnitude r = 500, rotated – 18° from the positive x – axis
Answer:
v = 〈1000 cos( – 126°), 1000 sin( – 126°) 〉; w = 〈500 cos( – 18)°, 500 sin( – 18°) 〉
v + w ≈ 〈 – 112.3, – 963.5〉
‖v + w‖ ≈ \(\sqrt{112.3^{2} + 963.5^{2}}\) ≈ 970.0
arctan \(\left(\frac{ – 963.5}{ – 112.3}\right)\) ≈ 83.4°
Since v + w lies in the third quadrant, it aligns with the terminal ray of rotation by
– (180° – 83.4°) = – 96.6°. The sum v + w has magnitude approximately 970 and direction – 96.6°
from the positive x – axis.
v – w ≈ 〈 – 1063.3, – 654.5〉
‖v – w‖ ≈ \(\sqrt{1063.3^{2} + 654.5^{2}}\) ≈ 1248.6
arctan \(\left(\frac{ – 654.5}{ – 1063.3}\right)\) ≈ 31.6°
Since v – w lies in the third quadrant, it aligns with the terminal ray of rotation by – (180° – 31.6°) = – 148.4°. The difference v – w has magnitude approximately 1248.6 and direction – 148.4° from the positive x – axis.
Question 5.
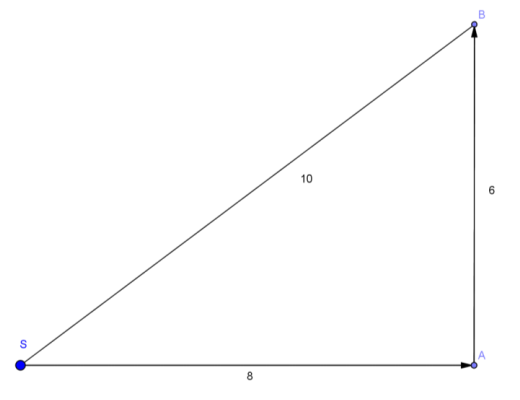
You hear a rattlesnake while out on a hike. You abruptly stop hiking at point S and take eight steps. Then you take another six steps. For each distance below, draw a sketch to show how the sum of your two displacements might add so that you find yourself that distance from point S. Assume that your steps are a uniform size.
a. 14 steps
Answer:

b. 10 steps
Answer:
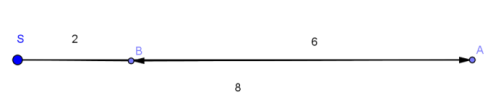
c. 2 steps
Answer:
Question 6.
A delivery driver travels 2.6 km due north, then 5.0 km due west, and then 4.2 km 45° north of west. How far is he from his starting location? Include a sketch with your answer.
Answer:
He is about 9.72 km from his starting location.

Question 7.
Morgan wants to swim directly across a river, from the east to the west side. She swims at a rate of 1 m/s. The current in the river is flowing due north at a rate of 3 m/s. Which direction should she swim so that she travels due west across the river?
Answer:
There is no way for Morgan to swim due west if she can only swim at a rate of 1 m/s. She would need to cancel out the north vector by swimming south at an equal rate (3 m/s). If she swims due south, she will still be swept downstream at a rate of 2 m/s.
Question 8.
A motorboat traveling at a speed of 4.0 m/s pointed east encounters a current flowing at a speed 3.0 m/s north.
a. What is the speed and direction that the motorboat travels?
Answer:
The motorboat is traveling 5 m/s at a direction 36.87° N of E.

b. What distance downstream does the boat reach the opposite shore?
Answer:
Since the vectors are perpendicular, the north flowing current does not affect the easterly direction and vice versa. It takes \(\frac{20}{4}\) = 5 seconds to reach the other side, and in that time the boat will have moved
3⋅5 = 15 m downstream.
Question 9.
A ball with mass 0.5 kg experiences a force F due to gravity of 4.9 newtons directed vertically downward. If this ball is rolling down a ramp that is 30° inclined from the horizontal, what is the magnitude of the force that is directed parallel to the ramp? Assume that the ball is small enough so that all forces are acting at the point of contact of the ball and the ramp.

Answer:
The diagram at right shows the forces that arise in this situation. We know that the magnitude of F is 4.9 N, and we need to find the magnitude of vector v. The three force vectors form a 30° – 60° – 90° triangle, so we know that

sin(30°) = \(\frac{\|\mathrm{v}\|}{\|\mathrm{F}\|}\)
Thus,
v = ‖F‖sin(30°)
= (4.9 N)sin(30°)
= 2.45 N.
Therefore, the force along the ramp has magnitude 2.45 newtons.
Question 10.
The stars in the Big Dipper may all appear to be the same distance from Earth, but they are, in fact, very far from each other. Distances between stars are measured in light years, the distance that light travels in one year. The star Alkaid at one end of the Big Dipper is 138 light years from Earth, and the star Dubhe at the other end of the Big Dipper is 105 light years from Earth. From Earth, it appears that Alkaid and Dubhe are 25.7° apart. Find the distance in light years between stars Alkaid and Dubhe.
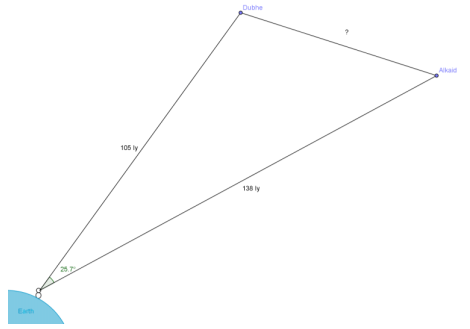
Answer:
The angle of elevation does not matter and the only thing that does is the angle between them. The distance between the two stars is the same no matter what angle we observe them, so we can treat the Alkaid star as being at a direction of 0° and the Dubhe star as being at a direction of 25.7°. Then we find the difference between the two vectors, and we find that the distance between them is about 62.9 light years.
Question 11.
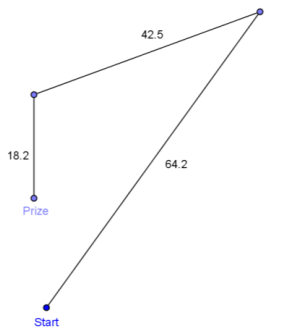
A radio station has selected three listeners to compete for a prize buried in a large, flat field. Starting in the center, the contestants are given a meter stick, a compass, a calculator, and a shovel. Each contestant is given the following three vectors, in a different order for each contestant.
64.2 m, 36° east of north
42.5 m, 20° south of west
18.2 m due south
The three displacements led to the point where the prize was buried. The contestant that found the prize first won. Instead of measuring immediately, the winner began by doing calculations on paper. What did she calculate?
Answer:
The winner calculated the sum of the three vectors. The prize is – 2.2 m to the west and 19.2 m to the north. This is only about 19.3 m away from the starting position, while someone following the directions blindly would travel a total of 124.9 m.
Eureka Math Precalculus Module 2 Lesson 20 Exit Ticket Answer Key
Question 1.
We saw in the lesson that the forces acting on a stone in a stable arch must sum to zero since the stones do not move. Consider the upper – left stone in a stable arch made of six stones. Denote this stone by S. In the image below, pL represents the force acting on stone S from the stone on the left. Vector pR represents the force acting on stone S from the stone on the right. Vector g represents the downward force of gravity.
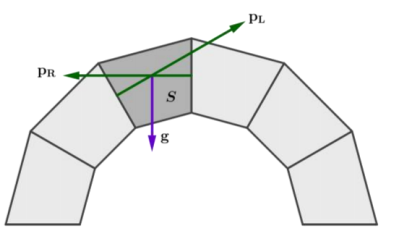
a. Describe the directions of vectors g, pL, and pR in terms of rotation from the positive x – axis by θ degrees, for – 180<θ≤180.
Answer:
Vector g is vertical, pointing downward, so g aligns with the terminal ray of rotation by –90°.
Vector pR is perpendicular to the vertical edge of the stone at point N, so it is horizontal and pointing to the left. Thus, pR aligns with the terminal ray of rotation by 180°.
Vector pL is perpendicular to line \(\overleftrightarrow{M Q}\) shown on the left. Thus, vector pL is rotated 120° from vertical. Hence, pL aligns with the terminal ray of rotation by 30° from horizontal.
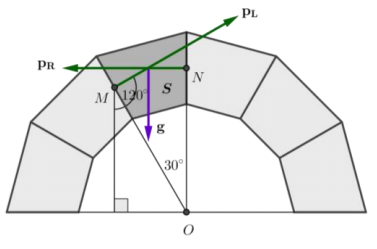
b. Suppose that vector g has a magnitude of 1. Find the magnitude of vectors pL and pR.
Answer:
We need to move the vectors tip – to – tail, and since the forces sum to zero, the vectors should make a triangle. Since g is vertical and pR is horizontal, the vectors make a right triangle.

By part (a), the angle made by vectors pR and pL measures 30°. We are given that ‖g‖ = 1. Then we know that sin(30°) = \(\frac{1}{\left\|p_{L}\right\|}\) ‖ , so \(\frac{1}{2}\) = \(\frac{1}{\left\|p_{L}\right\|}\) ‖ and then ‖ pL ‖ = 2.
Then cos(30°) = \(\frac{\left\|\mathrm{p}_{\mathrm{R}}\right\|}{\left\|\mathrm{p}_{\mathrm{L}}\right\|}\), so \(\frac{\sqrt{3}}{2}\) = \(\frac{\left\|\mathrm{p}_{\mathrm{R}}\right\|}{2}\) and ‖pR ‖ = \(\sqrt{3}\).
c. Write vectors g, pL, and pR in magnitude and direction form.
Answer:
Vector g has magnitude 1 and direction – 90° from the positive horizontal axis.
Vector pL has magnitude 2 and direction 30° from the positive horizontal axis.
Vector pR has magnitude \(\sqrt{3}\) and direction 180° from the positive horizontal axis.