Engage NY Eureka Math Precalculus Module 1 Lesson 7 Answer Key
Eureka Math Precalculus Module 1 Lesson 7 Exercise Answer Key
Opening Exercise
Perform the indicated operations. Write your answer in a+bi form. Identify the real part of your answer and the imaginary part of your answer.
a. (2+3i)+(-7-4i)
Answer:
-5-i, -5 is real, and -i is imaginary.
b. i2(-4i)
Answer:
4i, there is no real component, and 4i is imaginary.
c. 3i-(-2+5i)
Answer:
2-2i, 2 is real, and -2i is imaginary.
d. (3-2i)(-7+4i)
Answer:
-13+26i, -13 is real, and 26i is imaginary.
e. (-4-5i)(-4+5i)
Answer:
41, 41 is real, and there is no imaginary component.
Exercises
Exercise 1.
What is the multiplicative inverse of 2i?
Answer:
\(\frac{1}{2 i}\)=\(\frac{1}{2}\) ∙ \(\frac{1}{i}\) = \(\frac{1}{2}\) ∙ (-i)=-\(\frac{1}{2}\)i
Exercise 2.
Find the multiplicative inverse of 5+3i.
Answer:
\(\frac{5-3 i}{34}\)
State the conjugate of each number, and then using the general formula for the multiplicative inverse of z=a+bi, find the multiplicative inverse.
Exercise 3.
3+4i
Answer:
3-4i; \(\frac{3-4 i}{3^{2}+4^{2}}\)=\(\frac{3-4 i}{25}\)
Exercise 4.
7-2i
Answer:
7+2i; \(\frac{7-(-2) i}{7^{2}+(-2)^{2}}\)=\(\frac{7+2 i}{53}\)
Exercise 5.
i
Answer:
-i; \(\frac{0-1 i}{0^{2}+(1)^{2}}\)=\(\frac{-i}{1}\)=-i
Exercise 6.
2
Answer:
2; \(\frac{2-0 i}{2^{2}+0^{2}}\)=\(\frac{2}{4}\)=\(\frac{1}{2}\)
Exercise 7.
Show that a=-1+\(\sqrt{3}\)i and b=2 satisfy \(\frac{1}{a+b}\)=\(\frac{1}{a}\)+\(\frac{1}{b}\).
Answer:
Finding a common denominator of the right side, and then simplifying:
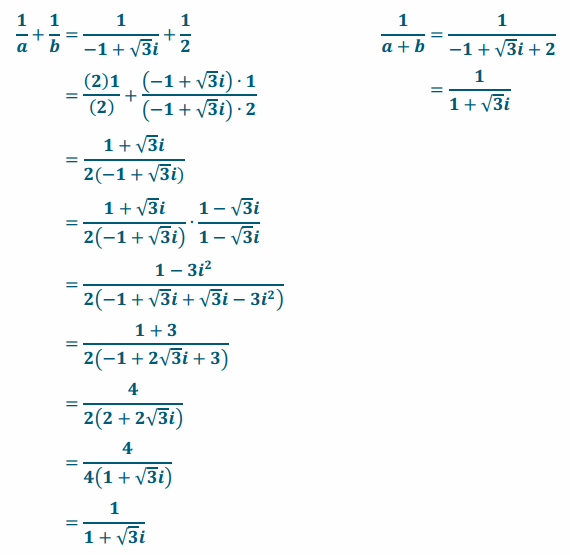
The two expressions are equal for the given values of a and b.
Eureka Math Precalculus Module 1 Lesson 7 Problem Set Answer Key
Problems 1 and 2 are easy entry problems that allow students to practice operations on complex numbers and the algebra involved in such operations, including solving systems of equations. These problems also reinforce that complex numbers have a real component and an imaginary component. Problem 3 is more difficult. Most students should attempt part (a), but part (b) is optional and sets the stage for the next lesson. All skills practiced in this Problem Set are essential for success in Lesson 8.
Question 1.
State the conjugate of each complex number. Then, find the multiplicative inverse of each number, and verify by multiplying by a+bi and solving a system of equations.
a. -5i
Answer:
Conjugate: 5i
-5i(a+bi)=1
-5ai-5bi2=1
-5ai+5b=1
-5a=0,5b=1
a=0,b=\(\frac{1}{5}\)
Multiplicative inverse: 0+\(\frac{1}{5}\)i=\(\frac{1}{5}\)i
b. 5-\(\sqrt{3}\)i
Answer:
Conjugate: (5+\(\sqrt{3}\)i)
(5-\(\sqrt{3}\)i)(a+bi)=1
5a+5bi-\(\sqrt{3}\)ai-\(\sqrt{3}\)bi2=1
5a+5bi-\(\sqrt{3}\)ai+\(\sqrt{3}\)b=1
5a+\(\sqrt{3}\)b=1,5b-\(\sqrt{3}\)a=0
a=\(\frac{5}{28}\),b=\(\frac{\sqrt{3}}{28}\)
Multiplicative Inverse: \(\frac{5+\sqrt{3} i}{28}\)
Question 2.
Find the multiplicative inverse of each number, and verify using the general formula to find multiplicative inverses of numbers of the form z=a+bi.
a. i3
Answer:
i3 =-i=0-i
Multiplicative inverse: \(\frac{0-(-1) i}{0^{2}+(-1)^{2}}\)=\(\frac{i}{1}\)=i
b. \(\frac{1}{3}\)
Answer:
\(\frac{1}{3}\)=\(\frac{1}{3}\)+0i
Multiplicative inverse: 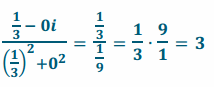
c. \(\frac{\sqrt{3}-i}{4}\)
Answer:
\(\frac{\sqrt{3}-i}{4}\) = \(\frac{\sqrt{3}}{4}\) + \(\frac{-1}{4}\)i
Multiplicative inverse: 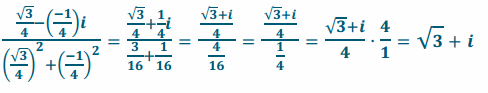
d. 1+2i
Answer:
Multiplicative inverse: \(\frac{1-2 i}{(1)^{2}+(-2)^{2}}\)=\(\frac{1-2 i}{5}\)=\(\frac{1}{5}\)–\(\frac{2 i}{5}\)
e. 4-3i
Answer:
Multiplicative inverse: \(\frac{4+3 i}{(4)^{2}+(-3)^{2}}\)=\(\frac{4+3 i}{25}\)=\(\frac{4}{25}\)+\(\frac{3 i}{25}\)
f. 2+3i
Answer:
Multiplicative inverse: \(\frac{2-3 i}{(2)^{2}+(-3)^{2}}\)=\(\frac{2-3 i}{13}\)=\(\frac{2}{13}\)–\(\frac{3 i}{13}\)
g. -5-4i
Answer:
Multiplicative inverse: \(\frac{-5+4 i}{(-5)^{2}+(-4)^{2}}\) = \(\frac{-5+4 i}{41}\)=\(-\frac{5}{41}\)+\(\frac{4 i}{41}\)
h. -3+2i
Answer:
Multiplicative inverse: \(\frac{-3-2 i}{(-3)^{2}+(2)^{2}}\)=\(\frac{-3-2 i}{13}\)=-\(\frac{3}{13}\)–\(\frac{2i}{13}\)
i. \(\sqrt{2}\)+i
Answer:
Multiplicative inverse: \(\)=\(\)=\(\)–\(\)
j. 3-\(\sqrt{2}\)∙i
Answer:
Multiplicative inverse: \(\frac{\sqrt{5}-\sqrt{3} i}{(\sqrt{5})^{2}+(-\sqrt{3})^{2}}\) = \(\frac{\sqrt{5}-\sqrt{3} i}{8}\) = \(\frac{\sqrt{5}}{8}\) – \(\frac{\sqrt{3} i}{8}\)
k. \(\sqrt{5}\)+\(\sqrt{3}\)∙i
Answer:
Multiplicative inverse: \(\frac{\sqrt{5}-\sqrt{3} i}{(\sqrt{5})^{2}+(-\sqrt{3})^{2}}\) = \(\frac{\sqrt{5}-\sqrt{3} i}{8}\) = \(\frac{\sqrt{5}}{8}\) – \(\frac{\sqrt{3} i}{8}\)
Question 3.
Given z1=1+i and z2=2+3i.
a. Let w=z1 ∙ z2. Find w and the multiplicative inverse of w.
Answer:
w=(1+i)(2+3i)=-1+5i
Multiplicative inverse: \(\frac{-1-5 i}{1+25}\) = –\(\frac{1}{26}\) – \(\frac{5i}{26}\)
b. Show that the multiplicative inverse of w is the same as the product of the multiplicative inverses of z1 and z2.
Answer:
z1=1+i; Multiplicative inverse: \(\frac{1-i}{1+1}\)=\(\)
z2=2+3i; Multiplicative inverse: \(\frac{2-3 i}{4+9}\)=\(\frac{2-3 i}{13}\)
z1 ∙ z2=(\(\frac{1-i}{2}\))(\(\frac{2-3 i}{13}\))
=\(\frac{2-3 i-2 i-3}{26}\)
=\(\frac{-1-5 i}{26}\)
=-\(\frac{1}{26}\)–\(\frac{5 i}{26}\)
Eureka Math Precalculus Module 1 Lesson 7 Exit Ticket Answer Key
Question 1.
Find the multiplicative inverse of 3-2i. Verify that your solution is correct by confirming that the product of 3-2i and its multiplicative inverse is 1.
Answer:
If a+bi is the multiplicative inverse of 3-2i, then
(3-2i)(a+bi)=1+0i(3-2i)(a+bi)
3a+3bi-2ai-2bi2=1+0i
3a+3bi-2ai+2b=1+0i.
3a+2b=1 and (3b-2a)i=0i, so 3b-2a=0.
a=\(\frac{3}{13}\), b=\(\frac{2}{13}\), so the multiplicative inverse a+bi=\(\frac{3+2i}{13}\).
Verification: (3-2i)(\(\frac{3}{13}\)+\(\frac{2i}{13}\))=\(\frac{9}{13}\)+\(\frac{6i}{13}\)–\(\frac{6i}{13}\)–\(\frac{4 i^{2}}{13}\)=\(\frac{9}{13}\)+\(\frac{4}{13}\)=1
Question 2.
What is the conjugate of 3-2i?
Answer:
3+2i