Engage NY Eureka Math Precalculus Module 1 Lesson 6 Answer Key
Eureka Math Precalculus Module 1 Lesson 6 Exercise Answer Key
Opening Exercise
Perform the indicated arithmetic operations for complex numbers z = -4 + 5i and w = -1-2i.
a. z + w
Answer:
z + w = -5 + 3i
b. z-w
Answer:
z-w = -3 + 7i
c.z + 2w
Answer:
z + 2w = -6 + i
d.z-z
Answer:
z-z = 0 + 0i
e. Explain how you add and subtract complex numbers.
Answer:
Add or subtract the real components and the imaginary components separately.
Exercises
Exercise 1.
The length of the vector that represents z1 = 6-8i is 10 because \(\sqrt{6^{2} + (-8)^{2}}\) = \(\sqrt{100}\) = 10.
a. Find at least seven other complex numbers that can be represented as vectors that have length 10.
Answer:
There are an infinite number of complex numbers that meet this criteria; the most obvious are 10, 6 + 8i, 8 + 6i, 10i, -6 + 8i, -8 + 6i, -10, -8-6i, -6-8i, -10i, 8-6i, and -8 + 6i. The associated vectors for these numbers are shown in the sample response for part (b).
b. Draw the vectors on the coordinate axes provided below.
Answer:
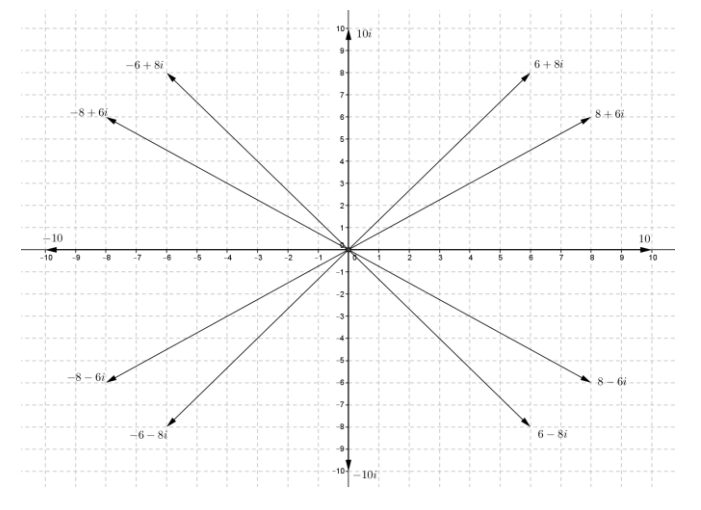
c. What do you observe about all of these vectors?
Answer:
Students should observe that the tips of the vectors lie on the circle of radius 10 centered at the origin.
Exercise 2.
In the Opening Exercise, we computed z + 2w. Calculate this sum using vectors.
Answer:
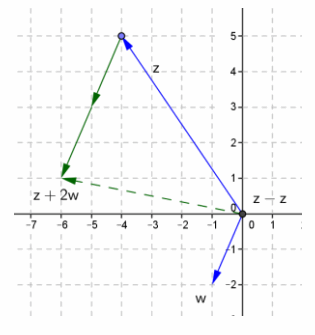
Exercise 3.
In the Opening Exercise, we also computed z-z. Calculate this sum using vectors.
Answer:
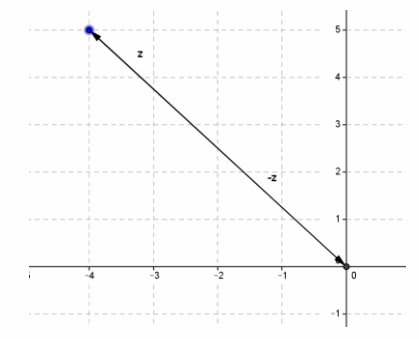
Exercise 4.
For the vectors u and v pictured below, draw the specified sum or difference on the coordinate axes provided.
a. u + v
b. v-u
c. 2u-v
d. -u-3v
Answer:
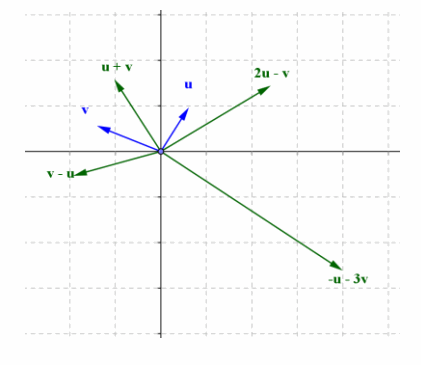
Exercise 5.
Find the sum of 4 + i and -3 + 2i geometrically.
Answer:
1 + 3i

Exercise 6.
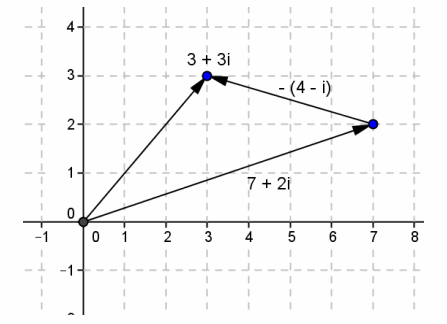
Show that (7 + 2i)-(4-i) = 3 + 3i by representing the complex numbers as vectors.
Answer:
Eureka Math Precalculus Module 1 Lesson 6 Problem Set Answer Key
Question 1.
Let z = 1 + i and w = 1-3i. Find the following. Express your answers in a + bi form.
a. z + w
Answer:
1 + i + 1-3i = 2-2i
b. z-w
Answer:
1 + i-(1-3i) = 1 + i-1 + 3i
= 0 + 4i
c. 4w
Answer:
4(1-3i) = 4-12i
d. 3z + w
Answer:
3(1 + i) + 1-3i = 3 + 3i + 1-3i
= 4 + 0i
e. -w-2z
Answer:
-(1-3i)-2(1 + i) = -1 + 3i-2-2i
= -3 + i
f. What is the length of the vector representing z?
Answer:
The length of the vector representing z is \(\sqrt{1^{2} + 1^{2}}\) = \(\sqrt{2}\).
g. What is the length of the vector representing w?
Answer:
The length of the vector representing w is \(\sqrt{1^{2} + (-3)^{2}}\) = \(\sqrt{10}\).
Question 2.
Let u = 3 + 2i, v = 1 + i, and w = -2-i. Find the following. Express your answer in a + bi form, and represent the result in the plane.
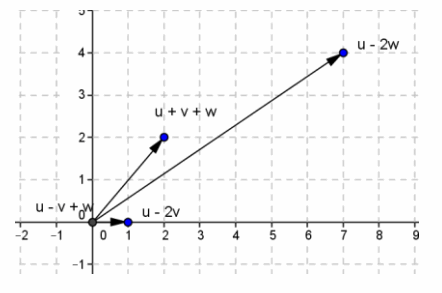
a. u-2v
Answer:
3 + 2i-2(1 + i) = 3 + 2i-2-2i
= 1 + 0i
b. u-2w
Answer:
3 + 2i-2(-2-i) = 3 + 2i + 4 + 2i
= 7 + 4i
c. u + v + w
Answer:
3 + 2i + 1 + i-2-i = 2 + 2i
d. u-v + w
Answer:
3 + 2i-(1 + i)-2-i = 3 + 2i-1-i-2-i
= 0 + 0i
e. What is the length of the vector representing u?
Answer:
The length of the vector representing u is \(\sqrt{3^{2} + 2^{2}}\) = \(\sqrt{13}\).
f. What is the length of the vector representing u-v + w?
Answer:
The length of the vector representing u-v + w = \(\sqrt{0^{2} + 0^{2}}\) = \(\sqrt{0}\) = 0.
Question 3.
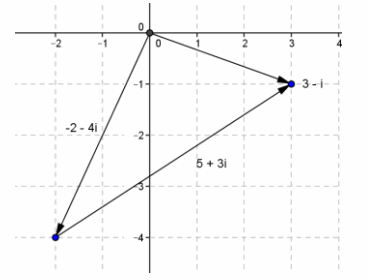
Find the sum of -2-4i and 5 + 3i geometrically.
Answer:
3-i
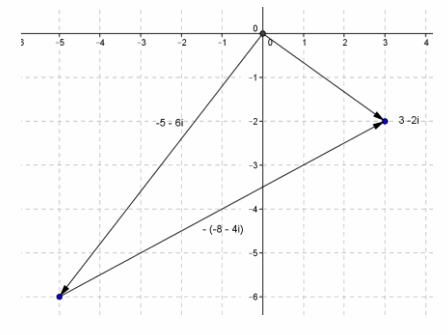
Question 4.
Show that (-5-6i)-(-8-4i) = 3-2i by representing the complex numbers as vectors.
Answer:
Question 5.
Let z1 = a1 + b1 i, z2 = a2 + b2 i, and z3 = a3 + b3 i. Prove the following using algebra or by showing with vectors.
Answer:
z1 + z2 = z2 + z1
z1 + z2 = (a1 + b1 i) + (a2 + b2 i)
= (a2 + b2 i) + (a1 + b1 i)
= z2 + z1
b. z1 + (z2 + z3 ) = (z1 + z2 ) + z3
Answer:
z1 + (z2 + z3 ) = (a1 + b1 i) + ((a2 + b2 i) + (a3 + b3 i))
= ((a1 + b1 i) + (a2 + b2 i)) + (a3 + b3 i)
= (z1 + z2 ) + z3
Question 6.
Let z = -3-4i and w = -3 + 4i.
a. Draw vectors representing z and w on the same set of axes.
Answer:
b. What are the lengths of the vectors representing z and w?
Answer:
The length of the vector representing z is \(\sqrt{(-3)^{2} + (-4)^{2}}\) = \(\sqrt{25}\) = 5.
The length of the vector representing w is \(\sqrt{(-3)^{2} + 4^{2}}\) = \(\sqrt{25}\) = 5.
c. Find a new vector, uz, such that uz is equal to z divided by the length of the vector representing z.
Answer:
uz = \(\frac{-3-4 i}{5}\) = \(\frac{-3}{5}\) – \(\frac{4}{5}\)i
d. Find uw, such that uw is equal to w divided by the length of the vector representing w.
Answer:
uw = \(\frac{-3 + 4 i}{5}\) = \(\frac{-3}{5}\) + \(\frac{4}{5}\)i
e. Draw vectors representing uz and uw on the same set of axes as part (a).
Answer:

f. What are the lengths of the vectors representing uz and uw?
Answer:
The length of the vector representing uz is \(\sqrt{\left(-\frac{3}{5}\right)^{2} + \left(-\frac{4}{5}\right)^{2}}\) = \(\sqrt{\frac{9}{25} + \frac{16}{25}}\) = \(\sqrt{\frac{25}{25}}\) = \(\sqrt{1}\) = 1.
The length of the vector representing uw is \(\sqrt{\left(-\frac{3}{5}\right)^{2} + \left(\frac{4}{5}\right)^{2}}\) = \(\sqrt{\frac{9}{25} + \frac{16}{25}}\) = \(\sqrt{\frac{25}{25}}\) = \(\sqrt{1}\) = 1.
g. Compare the vectors representing uz to z and uw to w. What do you notice?
Answer:
The vectors representing uz and uw are in the same direction as z and w, respectively, but their lengths are only 1.
h. What is the value of uz times uw?
Answer:
(\(\frac{3}{5}\)–\(\frac{4}{5}\)i)(\(\frac{3}{5}\))2-(\(\frac{4}{5}\)i)2 = (\(\frac{9}{25}\)) + (\(\frac{16}{25}\)) = 1
i. What does your answer to part (h) tell you about the relationship between uz and uw?
Answer:
Since their product is 1, we know that uz and uw are reciprocals of each other.
Question 7.
Let z = a + bi.
a. Let uz be represented by the vector in the direction of z with length 1. How can you find uz? What is the value of uz?
Answer:
Find the length of z, and then divide z by its length.
uz = \(\frac{a + b i}{\sqrt{a^{2} + b^{2}}}\)
b. Let uw be the complex number that when multiplied by uz, the product is 1. What is the value of uw?
Answer:
From Problem 4, we expect uw = \(\frac{a-b i}{\sqrt{a^{2} + b^{2}}}\). Multiplying, we get
\(\frac{a + b i}{\sqrt{a^{2} + b^{2}}}\) ∙ \(\frac{a-b i}{\sqrt{a^{2} + b^{2}}}\) = \(\frac{a^{2}-(b i)^{2}}{a^{2} + b^{2}}\)
= \(\frac{a^{2} + b^{2}}{a^{2} + b^{2}}\)
= 1
c. What number could we multiply z by to get a product of 1?
Answer:
Since we know that uz is equal to z divided by the length of z and that uz ∙ uw = 1, we get
z ∙ \(\frac{1}{\sqrt{a^{2} + b^{2}}}\)∙\(\frac{a-b i}{\sqrt{a^{2} + b^{2}}}\) = z∙\(\frac{a-b i}{a^{2} + b^{2}}\) = 1
So, multiplying z by \(\frac{a-b i}{a^{2} + b^{2}}\) will result in a product of 1.
Question 8.
Let z = -3 + 5i.
a. Draw a picture representing z + w = 8 + 2i.
Answer:

b. What is the value of w?
Answer:
w = 11 – 3i
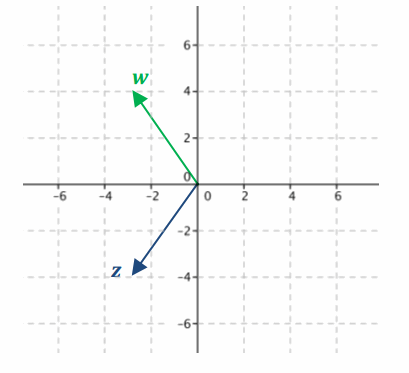
Eureka Math Precalculus Module 1 Lesson 6 Exit Ticket Answer Key
Answer:
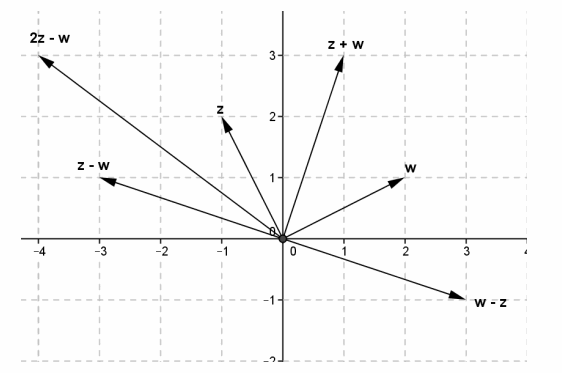
Let z = -1 + 2i and w = 2 + i. Find the following, and verify each geometrically by graphing z, w, and each result.
a. z + w
Answer:
1 + 3i
b. z-w
Answer:
-3 + i
c. 2z-w
Answer:
-4 + 3i
d. w-z
Answer:
3-i