Engage NY Eureka Math Precalculus Module 1 Lesson 4 Answer Key
Eureka Math Precalculus Module 1 Lesson 4 Exercise Answer Key
Opening Exercise
Is R(x) = \(\frac{1}{x}\) a linear transformation? Explain how you know.
Answer:
R(2+3) = R(5) = \(\frac{1}{5}\), but R(2)+R(3) = \(\frac{1}{2}\)+\(\frac{1}{3}\) = \(\frac{5}{6}\), which is not the same as \(\frac{1}{5}\). This means that the reciprocal function does not preserve addition, and so it is not a linear transformation.
Exercises
Exercise 1.
Solve 5x2 – 3x + 17 = 9.
Answer:
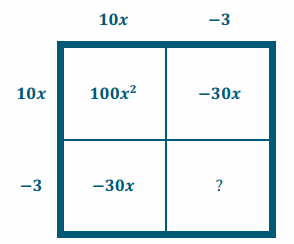
5x2 – 3x+17 = 9
5x2 – 3x = 9 – 17 = – 8
20(5x2 – 3x) = 20( – 8)
100x2 – 60x = – 160
100x2 – 60x+9 = – 160+9
(10x – 3)2 = – 151
x = \(\frac{3 \pm i \sqrt{151}}{10}\) = \(\frac{3}{10}\) ± i\(\frac{\sqrt{151}}{10}\)
Exercise 2.
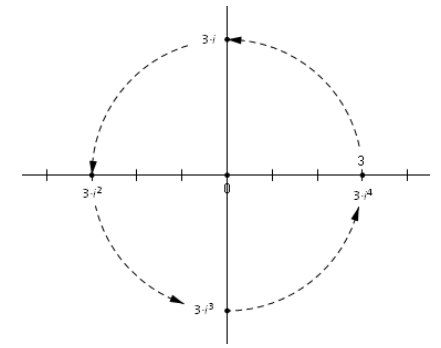
Use the fact that i2 = – 1 to show that i3 = – i. Interpret this statement geometrically.
Answer:
We have i3 = i2∙i = ( – 1)∙i = – i. Multiplying by i rotates a point through 90 degrees, and multiplying by – 1 rotates it 180 degrees farther. This makes sense with our earlier conjecture that multiplying by i3 would induce a 270 – degree rotation.
Exercise 3.
Calculate i6
Answer:
i6 = i2∙i2∙i2 = ( – 1)( – 1)( – 1) = (1)( – 1) = – 1
Exercise 4.
Calculate i5
Answer:
i5 = i2∙i2∙i = ( – 1)( – 1)(i) = (1)(i) = i
Eureka Math Precalculus Module 1 Lesson 4 Problem Set Answer Key
Question 1.
Solve the equation below.
5x2 – 7x+8 = 2
Answer:
5x2 – 7x = – 6
100x2 – 140x = – 120
100x2 – 140x+49 = – 120+49
(10x – 7)2 = – 71
x = \(\frac{7 \pm i \sqrt{71}}{10}\) = \(\frac{7}{10}\) ±i\(\frac{\sqrt{71}}{10}\)
Question 2.
Consider the equation x3 = 8.
a. What is the first solution that comes to mind?
Answer:
It is easy to see that 23 = 8, so 2 is a solution.
b. It may not be easy to tell at first, but this equation actually has three solutions. To find all three solutions, it is helpful to consider x3 – 8 = 0, which can be rewritten as (x – 2)(x2+2x+4) = 0 (check this for yourself). Find all of the solutions to this equation.
Answer:
x2+2x+4 = 0
x2+2x = – 4
x2+2x+1 = – 4+1
(x+1)2 = – 3
x = – 1±i\(\sqrt{3}\)
The solutions to x3 – 8 = 0 are 2, – 1+i\(\sqrt{3}\), and – 1 – i\(\sqrt{3}\).
Question 3.
Make a drawing that shows the first 5 powers of i (i.e., i1,i2,…,i5), and then confirm your results algebraically.
Answer:
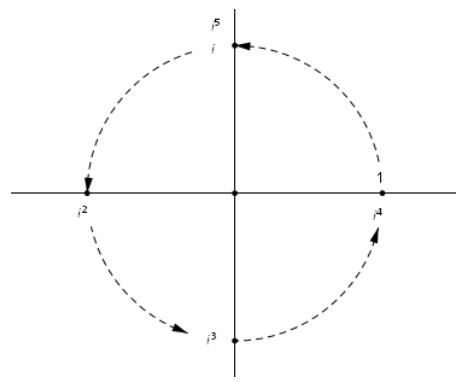
i1 = i
i2 = – 1
i3 = i2∙i = – 1∙i = – i
i4 = i2∙i2 = – 1∙ – 1 = 1
i5 = i4∙i = 1∙i = i
Question 4.
What is the value of i99? Explain your answer using words or drawings.
Answer:
Multiplying by i four times is equivalent to rotating through 4∙90 = 360 degrees, which is a complete rotation. Since 99 = 4∙24+3, multiplying by i for 99 times is equivalent to performing 24 complete rotations, followed by three 90 – degree rotations. Thus, i99 = – i.
Question 5.
What is the geometric effect of multiplying a number by – i? Does your answer make sense to you? Give an explanation using words or drawings.
Answer:
If we multiply a number by i and then by – 1, we get a quarter turn followed by a half turn. This is equivalent to a three – quarters turn in the counterclockwise direction, which is the same as a quarter turn in the clockwise direction. This makes sense because we would expect multiplication by – i to have the opposite effect as multiplication by i, and so it feels right to say that multiplying by – i rotates a point in the opposite direction by the same amount.

Eureka Math Precalculus Module 1 Lesson 4 Exit Ticket Answer Key
Question 1.
Solve the equation below.
2x2 – 3x+9 = 4
Answer:
2x2 – 3x = – 5
16x2 – 24x = – 40
16x2 – 24x+9 = – 40+9
(4x – 3)2 = – 31
4x – 3 = ±i\(\sqrt{31}\)
x = \(\frac{3 \pm i \sqrt{31}}{4}\) = \(\frac{3}{4}\)±i \(\frac{\sqrt{31}}{4}\)
Question 2.
What is the geometric effect of multiplying a number by i4? Explain your answer using words or pictures, and then confirm your answer algebraically.
Answer:
If you multiply a number by i four times, you would expect to see four 90 – degree rotations. This amounts to a
360 – degree rotation. In other words, each point is mapped back to itself. This makes sense algebraically as well since the work below shows that i4 = 1.
i4 = i2∙i2 = – 1∙ – 1 = 1