Engage NY Eureka Math Precalculus Module 1 Lesson 21 Answer Key
Eureka Math Precalculus Module 1 Lesson 21 Exercise Answer Key
Opening Exercise
Suppose that L1(x,y)=(2x-3y,3x+2y) and L2(x,y)=(3x+4y,-4y+3x).
Find the result of performing L1and then L2on a point (p,q). That is, find L2(L1(p,q)).
Answer:
L2(L1(p,q))=L2(2p-3q,3p+2q)
=(3(2p-3q)+4(3p+2q),-4(2p-3q)+3(3p+2q))
=(6p-9q+12p+8q,-8p+12q+9p+6q)
=(18p-q,p+18q)
Exercises
Exercise 1.
Calculate each of the following products.
a. \(\left(\begin{array}{cc}
3 & -2 \\
-1 & 4
\end{array}\right)\left(\begin{array}{l}
1 \\
5
\end{array}\right)\)
Answer:
\(\left(\begin{array}{c}
3-10 \\
-1+20
\end{array}\right)\) = \(\left(\begin{array}{c}
-7 \\
19
\end{array}\right)\)
b. \(\left(\begin{array}{ll}
3 & 3 \\
3 & 3
\end{array}\right)\left(\begin{array}{c}
4 \\
-4
\end{array}\right)\)
Answer:
\(\left(\begin{array}{ll}
3 & 3 \\
3 & 3
\end{array}\right)\left(\begin{array}{c}
4 \\
-4
\end{array}\right)\)\(\left(\begin{array}{l}
12-12 \\
12-12
\end{array}\right)\) = \(\left(\begin{array}{l}
\mathbf{0} \\
0
\end{array}\right)\)
c. \(\left(\begin{array}{ll}
2 & -4 \\
5 & -1
\end{array}\right)\left(\begin{array}{c}
3 \\
-2
\end{array}\right)\)
Answer:
\(\left(\begin{array}{cc}
2 & -4 \\
5 & -1
\end{array}\right)\left(\begin{array}{c}
3 \\
-2
\end{array}\right)\) = \(\) = \(\left(\begin{array}{l}
14 \\
17
\end{array}\right)\)
Exercise 2.
Find a value of k so that \(\left(\begin{array}{ll}
1 & 2 \\
k & 1
\end{array}\right)\left(\begin{array}{c}
3 \\
-1
\end{array}\right)\)=\(\left(\begin{array}{c}
1 \\
11
\end{array}\right)\).
Answer:
Multiplying this out, we have \(\left(\begin{array}{ll}
1 & 2 \\
k & 1
\end{array}\right)\left(\begin{array}{c}
3 \\
-1
\end{array}\right)\)=\(\left(\begin{array}{c}
\mathbf{1} \\
3 \boldsymbol{k}-\mathbf{1}
\end{array}\right)\)=\(\left(\begin{array}{c}
1 \\
11
\end{array}\right)\), so 3k-1=11, and thus, k=4.
Exercise 3.
Find a matrix \(\left(\begin{array}{ll}
a & b \\
c & d
\end{array}\right)\) so that we can represent the transformation L(x,y)=(2x-3y,3x+2y) by \(\).
Answer:
The matrix is \(\left(\begin{array}{cc}
2 & -3 \\
3 & 2
\end{array}\right)\).
Exercise 4.
If a transformation L\(\left(\begin{array}{l}
x \\
y
\end{array}\right)\)=\(\left(\begin{array}{ll}
a & b \\
c & d
\end{array}\right)\left(\begin{array}{l}
x \\
y
\end{array}\right)\) has the geometric effect of rotation and dilation, what do you know about the values a,b,c, and d?
Answer:
Since the transformation L(x,y)=(ax-by,bx+ay) has matrix representation L\(\left(\begin{array}{l}
x \\
y
\end{array}\right)\)=\(\left(\begin{array}{cc}
a & -b \\
b & a
\end{array}\right)\left(\begin{array}{l}
x \\
y
\end{array}\right)\), we know that a=d and c=-b.
Exercise 5.
Describe the form of a matrix \(\left(\begin{array}{ll}
a & b \\
c & d
\end{array}\right)\) so that the transformation L\(\left(\begin{array}{l}
x \\
y
\end{array}\right)\)=\(\left(\begin{array}{ll}
a & b \\
c & d
\end{array}\right)\left(\begin{array}{l}
x \\
y
\end{array}\right)\) has the geometric effect of only dilation by a scale factor r.
Answer:
The transformation that scales by factor r has the form L(x,y)=r(x,y)=(rx,ry)=(rx-0y,0x+ry), so the matrix has the form \(\left(\begin{array}{ll}
\boldsymbol{r} & \mathbf{0} \\
\mathbf{0} & \boldsymbol{r}
\end{array}\right)\).
Exercise 6.
Describe the form of a matrix \(\left(\begin{array}{ll}
a & b \\
c & d
\end{array}\right)\) so that the transformation L\(\left(\begin{array}{l}
x \\
y
\end{array}\right)\)=\(\left(\begin{array}{ll}
a & b \\
c & d
\end{array}\right)\left(\begin{array}{l}
x \\
y
\end{array}\right)\) has the geometric effect of only rotation by θ. Describe the matrix in terms of θ.
Answer:
The matrix has the form \(\left(\begin{array}{cc}
a & -b \\
b & a
\end{array}\right)\), where arg(a+bi)=θ. Thus, a=cos(θ) and b=sin(θ), so the matrix has the form \(\left(\begin{array}{cc}
\cos (\theta) & -\sin (\theta) \\
\sin (\theta) & \cos (\theta)
\end{array}\right)\).
Exercise 7.
Describe the form of a matrix \(\left(\begin{array}{ll}
a & b \\
c & d
\end{array}\right)\) so that the transformation L\(\left(\begin{array}{l}
x \\
y
\end{array}\right)\)=\(\left(\begin{array}{ll}
a & b \\
c & d
\end{array}\right)\left(\begin{array}{l}
x \\
y
\end{array}\right)\) has the geometric effect of rotation by θ and dilation with scale factor r. Describe the matrix in terms of θ and r.
Answer:
The matrix has the form \(\left(\begin{array}{cc}
a & -b \\
b & a
\end{array}\right)\), where arg(a+bi)=θ and r=|a+bi|. Thus, a=r cos(θ) and b=r sin(θ), so the matrix has the form \(\left(\begin{array}{cc}
r \cos (\theta) & -r \sin (\theta) \\
r \sin (\theta) & r \cos (\theta)
\end{array}\right)\).
Exercise 8.
Suppose that we have a transformation L\(\) = \(\).
a. Does this transformation have the geometric effect of rotation and dilation?
Answer:
No, the matrix is not in the form \(\), so this transformation is not a rotation and dilation.
b. Transform each of the points A=\(\left(\begin{array}{l}
0 \\
0
\end{array}\right)\), B = \(\left(\begin{array}{l}
1 \\
0
\end{array}\right)\), C = \(\left(\begin{array}{l}
1 \\
1
\end{array}\right)\), and D = \(\left(\begin{array}{l}
0 \\
1
\end{array}\right)\) and plot the images in the plane shown.
Answer:
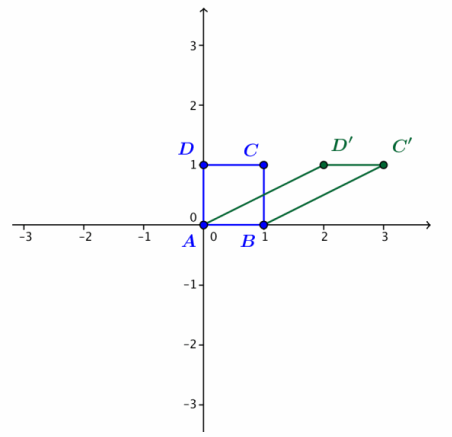
Exercise 9.
Describe the geometric effect of the transformation L\(\left(\begin{array}{l}
x \\
y
\end{array}\right)\)=\(\left(\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right)\left(\begin{array}{l}
x \\
y
\end{array}\right)\).
Answer:
This transformation does nothing to the point (x,y) in the plane; it is the identity transformation.
Eureka Math Precalculus Module 1 Lesson 21 Problem Set Answer Key
Question 1.
Perform the indicated multiplication.
a. \(\left(\begin{array}{ll}
1 & 2 \\
4 & 8
\end{array}\right)\left(\begin{array}{c}
3 \\
-2
\end{array}\right)\)
Answer:
\(\left(\begin{array}{l}
-1 \\
-4
\end{array}\right)\)
b. \(\left(\begin{array}{cc}
3 & 5 \\
-2 & -6
\end{array}\right)\left(\begin{array}{l}
2 \\
4
\end{array}\right)\)
Answer:
\(\left(\begin{array}{c}
26 \\
-28
\end{array}\right)\)
c. \(\left(\begin{array}{cc}
1 & 1 \\
1 & -1
\end{array}\right)\left(\begin{array}{l}
6 \\
8
\end{array}\right)\)
Answer:
\(\left(\begin{array}{l}
14 \\
-2
\end{array}\right)\)
d. \(\left(\begin{array}{ll}
5 & 7 \\
4 & 9
\end{array}\right)\left(\begin{array}{c}
10 \\
100
\end{array}\right)\)
Answer:
\(\left(\begin{array}{l}
750 \\
940
\end{array}\right)\)
e. \(\left(\begin{array}{ll}
4 & 2 \\
3 & 7
\end{array}\right)\left(\begin{array}{c}
-3 \\
1
\end{array}\right)\)
Answer:
\(\left(\begin{array}{c}
-10 \\
-2
\end{array}\right)\)
f. \(\left(\begin{array}{ll}
6 & 4 \\
9 & 6
\end{array}\right)\left(\begin{array}{c}
2 \\
-3
\end{array}\right)\)
Answer:
\(\left(\begin{array}{l}
\mathbf{0} \\
0
\end{array}\right)\)
g. \(\left(\begin{array}{cc}
\cos (\theta) & -\sin (\theta) \\
\sin (\theta) & \cos (\theta)
\end{array}\right)\left(\begin{array}{l}
x \\
y
\end{array}\right)\)
Answer:
\(\left(\begin{array}{l}
x \cos (\theta)-y \sin (\theta) \\
x \sin (\theta)+y \cos (\theta)
\end{array}\right)\)
h. \(\left(\begin{array}{cc}
\pi & 1 \\
1 & -\pi
\end{array}\right)\left(\begin{array}{c}
10 \\
7
\end{array}\right)\)
Answer:
\(\left(\begin{array}{l}
10 \pi+7 \\
10-7 \pi
\end{array}\right)\)
Question 2.
Find a value of k so that ![]() .
.
Answer:
We have ![]() , so 4k+15=7 and 16+5k=6. Thus, 4k=-8 and 5k=-10, so
, so 4k+15=7 and 16+5k=6. Thus, 4k=-8 and 5k=-10, so
k=-2.
Question 3.
Find values of k and m so that ![]() .
.
Answer:
We have 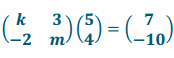 , so 5k+12=7 and -10+4m=-10. Therefore, k=-1 and m=0.
, so 5k+12=7 and -10+4m=-10. Therefore, k=-1 and m=0.
Question 4.
Find values of k and m so that ![]() .
.
Answer:
Since ![]() , we need to find values of k and m so that k+2m=0 and
, we need to find values of k and m so that k+2m=0 and
-2k+5m=-9. Solving this first equation for k gives k=-2m, and substituting this expression for k into the second equation gives –9=-2(-2m)+5m=9m, so we have m=-1. Then, k=-2m gives k=2. Therefore, k=2 and m=-1.
Question 5.
Write the following transformations using matrix multiplication.
a. L(x,y)=(3x-2y,4x-5y)
Answer:
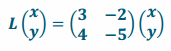
b. L(x,y)=(6x+10y,-2x+y)
Answer:
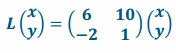
c. L(x,y)=(25x+10y,8x-64y)
Answer:
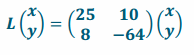
d. L(x,y)=(πx-y,-2x+3y)
Answer:
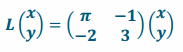
e. L(x,y)=(10x,100x)
Answer:
![]()
f. L(x,y)=(2y,7x)
Answer:
![]()
Question 6.
Identify whether or not the following transformations have the geometric effect of rotation only, dilation only, rotation and dilation only, or none of these.
a. 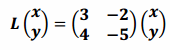
Answer:
The matrix ![]() cannot be written in the form
cannot be written in the form ![]() , because 3≠-5, so this is neither a rotation nor a dilation. The transformation L is not one of the specified types of transformations.
, because 3≠-5, so this is neither a rotation nor a dilation. The transformation L is not one of the specified types of transformations.
b. 
Answer:
This transformation has the geometric effect of dilation by a scale factor of 42.
c. 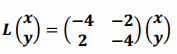
Answer:
The matrix ![]() has the form
has the form ![]() with a=-4 and b=2. Therefore, this transformation has the geometric effect of rotation and dilation.
with a=-4 and b=2. Therefore, this transformation has the geometric effect of rotation and dilation.
d. 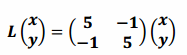
The matrix ![]() cannot be written in the form
cannot be written in the form ![]() , because -1≠-(-1), so this is neither a rotation nor a dilation. The transformation L is not one of the specified types of transformations.
, because -1≠-(-1), so this is neither a rotation nor a dilation. The transformation L is not one of the specified types of transformations.
e. 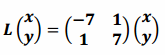
Answer:
The matrix ![]() cannot be written in the form
cannot be written in the form ![]() , because -7≠7, so this is neither a rotation nor a dilation. The transformation L is not one of the specified types of transformations.
, because -7≠7, so this is neither a rotation nor a dilation. The transformation L is not one of the specified types of transformations.
f. 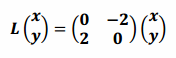
Answer:
We see that 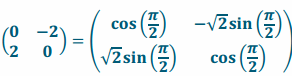 , so this transformation has the geometric effect of dilation by \(\sqrt{2}\) and rotation by \(\frac{\pi}{2}\).
, so this transformation has the geometric effect of dilation by \(\sqrt{2}\) and rotation by \(\frac{\pi}{2}\).
Question 7.
Create a matrix representation of a linear transformation that has the specified geometric effect.
a. Dilation by a factor of 4 and no rotation
Answer:
![]()
b. Rotation by 180° and no dilation
Answer:

c. Rotation by –\(\frac{π}{2}\)rad and dilation by a scale factor of 3
Answer:
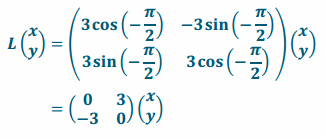
d. Rotation by 30° and dilation by a scale factor of 4
Answer:

Question 8.
Identify the geometric effect of the following transformations. Justify your answers.
a. 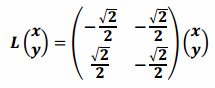
Answer:
Since ![]() , this transformation has the form
, this transformation has the form
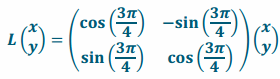 and, thus, represents counterclockwise rotation by \(\frac{3π}{4}\) with no dilation.
and, thus, represents counterclockwise rotation by \(\frac{3π}{4}\) with no dilation.
b. 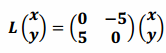
Answer:
Since cos(\(\frac{π}{2}\))=0 and sin(\(\frac{π}{2}\))=1, this transformation has the form 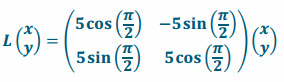 and, thus, represents counterclockwise rotation by \(\frac{π}{2}\) and dilation by a scale factor 5.
and, thus, represents counterclockwise rotation by \(\frac{π}{2}\) and dilation by a scale factor 5.
c. 
Answer:
Since cos(π)=-1 and sin(π)=0, this transformation has the form
![]() and, thus, represents counterclockwise rotation by π and dilation by a scale factor 10.
and, thus, represents counterclockwise rotation by π and dilation by a scale factor 10.
d. 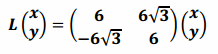
Answer:
Since cos(\(\frac{5π}{3}\))=\(\frac{1}{2}\) and sin(\(\frac{5π}{3}\))=-\(\frac{\sqrt{3}}{2}\), this transformation has the form
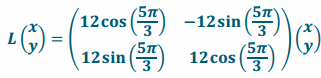 and, thus, represents counterclockwise rotation by \(\frac{5π}{3}\) and dilation with scale factor 12.
and, thus, represents counterclockwise rotation by \(\frac{5π}{3}\) and dilation with scale factor 12.
Eureka Math Precalculus Module 1 Lesson 21 Exit Ticket Answer Key
Question 1.
Evaluate the product \(\left(\begin{array}{cc}
10 & 2 \\
-8 & -5
\end{array}\right)\left(\begin{array}{c}
3 \\
-2
\end{array}\right)\).
Answer:
\(\left(\begin{array}{cc}
10 & 2 \\
-8 & -5
\end{array}\right)\left(\begin{array}{c}
3 \\
-2
\end{array}\right)\) = \(\left(\begin{array}{c}
30-4 \\
-24+10
\end{array}\right)\)
= \(\left(\begin{array}{c}
26 \\
-14
\end{array}\right)\)
Question 2.
Find a matrix representation of the transformation L(x,y)=(3x+4y,x-2y).
Answer:
L\(\left(\begin{array}{l}
x \\
y
\end{array}\right)\) = \(\left(\begin{array}{cc}
3 & 4 \\
1 & -2
\end{array}\right)\left(\begin{array}{l}
x \\
y
\end{array}\right)\)
Question 3.
Does the transformation L\(\left(\begin{array}{l}
x \\
y
\end{array}\right)\)= \(\left(\begin{array}{cc}
5 & 2 \\
-2 & 5
\end{array}\right)\left(\begin{array}{l}
x \\
y
\end{array}\right)\) represent a rotation and dilation in the plane? Explain how you know.
Answer:
Yes; this transformation can also be represented as L(x,y)=(5x-(-2)y,-2x+5y), which has the geometric effect of counterclockwise rotation by arg(5-2i) and dilation by |5-2i|.