Engage NY Eureka Math Precalculus Module 1 Lesson 20 Answer Key
Eureka Math Precalculus Module 1 Lesson 20 Exercise Answer Key
Opening Exercise
a. Find a complex number w so that the transformation L1(z)=wz produces a clockwise rotation by 1° about the origin with no dilation.
Because there is no dilation, we need |w|=1, and because there is rotation by 1°, we need arg(w)=1°. Thus, we need to find the point where the terminal ray of a 1° rotation intersects the unit circle.
From Algebra II, we know the coordinates of the point are
(x,y)=(cos(1°),sin(1°)),
so that the complex number w is
w=x+iy=cos(1°)+isin(1°).
(Students may use a calculator to find the approximation w=0.99998+0.01745i.)
b. Find a complex number w so that the transformation L2(z)=wz produces a dilation with scale factor 0.1 with no rotation.
Answer:
In this case, there is no rotation, so the argument of w must be 0. This means that the complex number w corresponds to a point on the positive real axis, so w has no imaginary part; this means that w is a real number, and w=a+bi=a. Thus, |w|=a=0.1, so w=0.1.
Exercises
Exercise 1.
a. Find values of a and b so that L1(x,y)=(ax-by,bx+ay) has the effect of dilation with scale factor 2 and no rotation.
Answer:
We need arg(a+bi)=0 and \(\sqrt{a^{2}+b^{2}}\)=2. Since arg(a+bi)=0, the point corresponding to a+bi lies along the positive x-axis, so we know that b=0 and a>0. Then, we have \(\sqrt{a^{2}+b^{2}}\)=\(\sqrt{a^{2}}\)=a, so a=2. Thus, the transformation L1(x,y)=(2x-0y,0x+2y)=(2x,2y) has the geometric effect of dilation by scale factor 2.
b. Evaluate L1(L1(x,y)), and identify the resulting transformation.
Answer:
L1(L1(x,y))=L1(2x,2y)
=(4x,4y)
If we take L1(L1(x,y)), we are dilating the point (x,y) with scale factor 2 twice. This means that we are dilating with scale factor 2 ∙ 2=4.
Exercise 2.
Find values of a and b so that L2(x,y)=(ax-by,bx+ay) has the effect of rotation about the origin by 180° counterclockwise and no dilation.
Since there is no dilation, we have \(\sqrt{a^{2}+b^{2}}\)=1, and arg(a+bi)=180° means that the point (a,b) lies on the negative x-axis. Then, a<0 and b=0, so \(\sqrt{a^{2}+b^{2}}\)=\(\sqrt{a^{2}}\)=|a|=1, so a=-1. Then, the transformation L2(x,y)=(-x-0y,0x-y)=(-x,-y) has the geometric effect of rotation by 180° without dilation.
b. Evaluate L2(L2(x,y)), and identify the resulting transformation.
Answer:
L2(L2(x,y))=L2(-x,-y)
=(-(-x),-(-y))
=(x,y)
Thus, if we take L2(L2(x,y)), we are rotating the point (x,y) by 180° twice, which results in a rotation of 360° and has the net effect of doing nothing to the point (x,y). This is the identity transformation.
Exercise 3.
a. Find values of a and b so that L3(x,y)=(ax-by,bx+ay) has the effect of rotation about the origin by 90° counterclockwise and no dilation.
Answer:
Since there is no dilation, we have \(\sqrt{a^{2}+b^{2}}\)=1, and since the rotation is 90° counterclockwise, we know that a+bi must lie on the positive imaginary axis. Thus, a=0, and we must have b=1. Then, the transformation L3(x,y)=(0x-y,x+0y)=(-y,x) has the geometric effect of rotation by 90° counterclockwise with no dilation.
b. Evaluate L3(L3(x,y)), and identify the resulting transformation.
Answer:
L3(L3(x,y))=L3(-y,x)
=(-x,-y)
=L2(x,y)
Thus, if we take L3(L3(x,y)), we are rotating the point (x,y) by 90° twice, which results in a rotation of 180°. This is the transformation L2.
Exercise 4.
Find values of a and b so that L3(x,y)=(ax-by,bx+ay) has the effect of rotation about the origin by 45° counterclockwise and no dilation.
Answer:
Since there is no dilation, we have \(\)=1, and since the rotation is 45° counterclockwise, we know that the point (a,b) lies on the line y=x, and thus, a=b. Then, \(\sqrt{a^{2}+b^{2}}\)=\(\sqrt{a^{2}+a^{2}}\)=1, so 2a2=1, and thus a=\(\frac{\sqrt{2}}{2}\), so we also have b=\(\frac{\sqrt{2}}{2}\). Then, the transformation L(x,y)=(\(\frac{\sqrt{2}}{2}\) x-\(\frac{\sqrt{2}}{2}\)y,\(\frac{\sqrt{2}}{2}\)x+\(\frac{\sqrt{2}}{2}\)y) has the geometric effect of rotation by 45° counterclockwise with no dilation.
(Students may also find the values of a and b by +bi=cos(45°)+isin(45°).)
b. Evaluate L4(L4(x,y)), and identify the resulting transformation.
We then have
Answer:
L4(L4(x,y))=L4(\(\frac{\sqrt{2}}{2}\) x-\(\frac{\sqrt{2}}{2}\) y,\(\frac{\sqrt{2}}{2}\) x+\(\frac{\sqrt{2}}{2}\) y)
=(\(\frac{\sqrt{2}}{2}\) (\(\frac{\sqrt{2}}{2}\) x-\(\frac{\sqrt{2}}{2}\) y)-\(\frac{\sqrt{2}}{2}\) (\(\frac{\sqrt{2}}{2}\) x+\(\frac{\sqrt{2}}{2}\) y),\(\frac{\sqrt{2}}{2}\) (\(\frac{\sqrt{2}}{2}\) x-\(\frac{\sqrt{2}}{2}\) y)+\(\frac{\sqrt{2}}{2}\) (\(\frac{\sqrt{2}}{2}\) x+\(\frac{\sqrt{2}}{2}\) y))
=((\(\frac{1}{2}\)x-\(\frac{1}{2}\)y)-(\(\frac{1}{2}\)x+\(\frac{1}{2}\)y),(\(\frac{1}{2}\)x-\(\frac{1}{2}\)y)+(\(\frac{1}{2}\)x+\(\frac{1}{2}\)y))
=(-y,x)
=L3(x,y)
Thus, if we take L4(L4(x,y)), we are rotating the point (x,y) by 45° twice, which results in a rotation of 90°. This is the transformation L3.
Exercise 5.
The figure below shows a quadrilateral with vertices A(0,0), B(1,0), C(3,3), and D(0,3).
a. Transform each vertex under L5=(3x+y,3y-x), and plot the transformed vertices on the figure.
Answer:
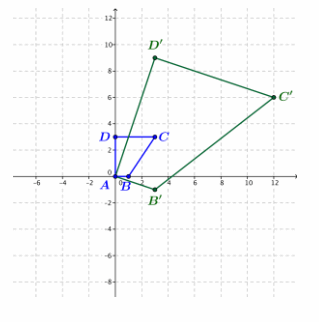
b. Does L5 represent a rotation and dilation? If so, estimate the amount of rotation and the scale factor from your figure.
Answer:
The transformed image is roughly three times larger than the original and rotated about 20° clockwise.
c. If L5 represents a rotation and dilation, calculate the amount of rotation and the scale factor from the formula for L5. Do your numbers agree with your estimate in part (b)? If not, explain why there are no values of a and b so that L5 (x,y)=(ax-by,bx+ay).
Answer:
From the formula, we have a=3 and b=-1. The transformation dilates by the scale factor
|a+bi|=\(\sqrt{3^{3}+(-1)^{2}}\)=\(\sqrt{10}\)≈3.16 and rotates by
arg(a+bi)=arctan(\(\frac{\boldsymbol{b}}{\boldsymbol{a}}\))=arctan(-\(\frac{\boldsymbol{1}}{\boldsymbol{3}}\)))≈-18.435°.
Exercise 6.
The figure below shows a figure with vertices A(0,0), B(1,0), C(3,3), and D(0,3).
a. Transform each vertex under L6=(2x+2y,2x-2y), and plot the transformed vertices on the figure.
Answer:
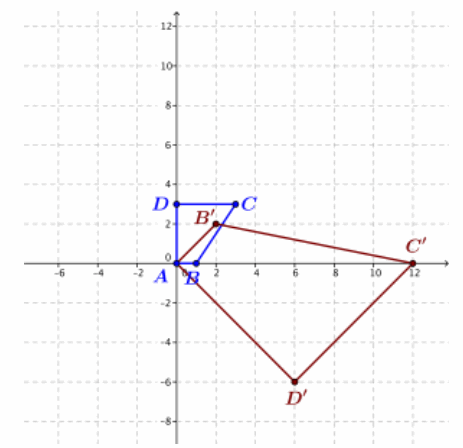
b. Does L6 represent a rotation and dilation? If so, estimate the amount of rotation and the scale factor from your figure.
Answer:
The transformed image is dilated and rotated but is also reflected, so transformation L6 is not a rotation and dilation.
c. If L5 represents a rotation and dilation, calculate the amount of rotation and the scale factor from the formula for L6. Do your numbers agree with your estimate in part (b)? If not, explain why there are no values of a and b so that L6 (x,y)=(ax-by,bx+ay).
Answer:
Suppose that (2x+2y,2x-2y)=(ax-by,bx+ay). Then, a=2 and a=-2, which is not possible. This transformation does not fit our formula for rotation and dilation.
Eureka Math Precalculus Module 1 Lesson 20 Problem Set Answer Key
Question 1.
Find real numbers a and b so that the transformation L(x,y)=(ax-by,bx+ay) produces the specified rotation and dilation.
a. Rotation by 270° counterclockwise and dilation by scale factor \(\frac{1}{2}\).
Answer:
We need to find real numbers a and b so that a+bi has modulus \(\frac{1}{2}\)and argument 270°. Then, (a,b) lies on the negative y-axis, so a=0 and b<0. We need \(\frac{1}{2}\)=|a+bi|=|bi|=|b|, so this means that b=-\(\frac{1}{2}\). Thus, the transformation L(x,y)=(\(\frac{1}{2}\)y,-\(\frac{1}{2}\)x) will rotate by 270° and dilate by a scale factor of \(\frac{1}{2}\). b. Rotation by 135° counterclockwise and dilation by scale factor \(\sqrt{2}\). Answer: We need to find real numbers a and b so that a+bi has modulus \(\sqrt{2}\) and argument 135°. Thus, (a,b) lies in the second quadrant on the diagonal line with equation y=-x, so we know that a>0 and b=-a. Since \(\sqrt{2}\)=\(\sqrt{a^{2}+(-a)^{2}}\) and a=-b, we have \(\sqrt{2}\)=\(\sqrt{2 a^{2}}\) so \(\sqrt{2}\)=\(\sqrt{2 a^{2}}\), and thus a=1. It follows that b=-1. Then, the transformation L(x,y)=(x+y,-x+y) rotates by 135° counterclockwise and dilates by a scale factor of \(\sqrt{2}\).
c. Rotation by 45° clockwise and dilation by scale factor 10.
Answer:
We need to find real numbers a and b so that a+bi has modulus 10 and argument 45°. Thus, (a,b) lies in the first quadrant on the line with equation y=x, so we know that a=b and a>0, b>0. Since 10=\(\sqrt{\left(a^{2}+b^{2}\right)}\)=\(\sqrt{a^{2}+a^{2}}\), we know that 2a2=100, and a=b=5\(\sqrt{2}\). Thus, the transformation L(x,y)=(5\(\sqrt{2}\) x-5\(\sqrt{2}\) y,5\(\sqrt{2}\) x+5\(\sqrt{2}\) y) rotates by 45° counterclockwise and dilates by a scale factor of 10.
d. Rotation by 540° counterclockwise and dilation by scale factor 4.
Answer:
Rotation by 540° counterclockwise has the same effect as rotation by 180° counterclockwise. Thus, we need to find real numbers a and b so that the argument of (a+bi) is 180° and |a+bi|=√(a2+b2 )=4. Since arg(a+bi)=180°, we know that the point (a,b) lies on the negative x-axis, and we have a<0 and b=0. We then have a=-4 and b=0, so the transformation L(x,y)=(-4x,-4y) will rotate by 540° counterclockwise and dilate with scale factor 4.
Question 2.
Determine if the following transformations represent a rotation and dilation. If so, identify the scale factor and the amount of rotation.
a. L(x,y)=(3x+4y,4x+3y)
Answer:
If L(x,y) is of the form(x,y)=(ax-by,bx+ay), then a=3 and b must be both 3 and –3. Since this is impossible, this transformation does not consist of rotation and dilation.
b. L(x,y)=(-5x+12y,-12x-5y)
Answer:
If we let a=-5 and b=-12, then L(x,y) is of the form (x,y)=(ax-by,bx+ay). Thus, this transformation does consist of rotation and dilation. The dilation has scale factor \(\sqrt{(-5)^{2}+(-12)^{2}}\)=13,
and the transformation rotates through arg(-5-12i)=arctan(\(\frac{12}{5}\))≈67.38°.
c. L(x,y)=(3x+3y,-3y+3x)
Answer:
If we let a=3 and b=-3, then L(x,y) is of the form (x,y)=(ax-by,bx+ay). Thus, the transformation does consist of rotation and dilation. The dilation has scale factor \(\sqrt{(3)^{2}+(-3)^{2}}\)=3\(\sqrt{2}\), and the transformation rotates through arg(3-3i)=315°.
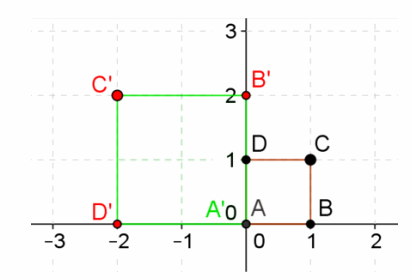
Question 3.
Grace and Lily have a different point of view about the transformation on cube ABCD that is shown above. Grace states that it is a reflection about the imaginary axis and a dilation of factor of 2. However, Lily argues it should be a 90° counterclockwise rotation about the origin with a dilation of a factor of 2.
a. Who is correct? Justify your answer.
Answer:
Lily is correct because the vertices of the cube stay the same with respect to each other.
b. Represent the above transformation in the form L(x,y)=(ax-by,bx+ay).
Answer:
Rotating 90° with a dilation of a factor of 2: a+bi=2(cos(90°)+i∙sin(90°))=2(0+1i)=0+2i.
Therefore, a=0,b=2,L(x,y)=(0x-2y,2x+0y)=(-2y,2x).
Question 4.
Grace and Lily still have a different point of view on this transformation on triangle ABC shown above. Grace states that it is reflected about the real axis first, then reflected about the imaginary axis, and then dilated with a factor of 2. However, Lily asserts that it is a 180° counterclockwise rotation about the origin with a dilation of a factor of 2.
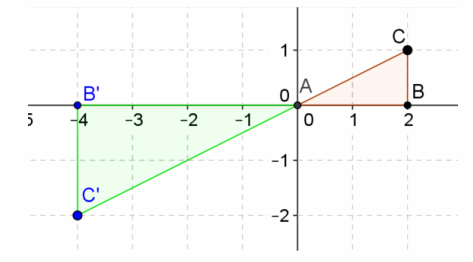
a. Who is correct? Justify your answer.
Answer:
Both are correct. Both sequences of transformations result in the same image.
b. Represent the above transformation in the form L(x,y)=(ax-by,bx+ay).
Answer:
Rotating 180° with a dilation of a factor of 2:
a+bi=2(cos(180°)+i∙sin(180°))=2(-1+0i)=-2+0i.
Therefore, a-2,b=0,L(x,y)=(-2x-0y,0x-2y)=(-2x,-2y).
Question 5.
Given z=\(\sqrt{3}\)+i
a. Find the complex number w that will cause a rotation with the same number of degrees as z without a dilation.
Answer:
z=\(\sqrt{3}\)+i,|z|=2,w=\(\frac{1}{2}\)(\(\sqrt{3}\)+i)
b. Can you come up with a general formula L(x,y)=(ax-by,bx+ay) for any complex number z=x+yi to represent this condition?
Answer:
w=x+yi,|z|=\(\sqrt{x^{2}+y^{2}}\),a=x,b=y,
L(x,y)=\(\frac{1}{\sqrt{x^{2}+y^{2}}}\)(x∙x-y∙y,y∙x+x∙y)=\(\frac{1}{\sqrt{x^{2}+y^{2}}}\)(x2-y2,2xy)
Eureka Math Precalculus Module 1 Lesson 20 Exit Ticket Answer Key
Question 1.
Find the scale factor and rotation induced by the transformation L(x,y)=(-6x-8y,8x-6y).
Answer:
This is a transformation of the form L(x,y)=(ax-by,bx+ay) with a=-6 and b=8. The scale factor is then \(\sqrt{(-6)^{2}+8^{2}}\)=10.
The rotation is the arctan(\(\frac{8}{-6}\))≈-51.13°.
Question 2.
Explain how the transformation of complex numbers L(x+iy)=(a+bi)(x+iy) leads to the transformation of points in the coordinate plane L(x,y)=(ax-by,bx+ay).
Answer:
First, we associate the complex number x+iy to the point (x,y) in the coordinate plane. Then, the point associated with the complex number (a+bi)(x+iy)=(ax-by)+(bx+ay)i is (ax-by,bx+ay). Thus, we can interpret the original transformation of complex numbers as the transformation of points
L(x,y)=(ax-by,bx+ay).