Engage NY Eureka Math Precalculus Module 1 Lesson 16 Answer Key
Eureka Math Precalculus Module 1 Lesson 16 Exercise Answer Key
Opening Exercise
a. Find a transformation R(0,45°):C→C that rotates a point represented by the complex number z by 45° counterclockwise in the coordinate plane but does not produce a dilation.
Answer:
L(z)=(\(\frac{\sqrt{2}}{2}\)+i\(\frac{\sqrt{2}}{2}\))z
b. Find a transformation R(0,-45°):C→C that rotates a point represented by the complex number z by 45° clockwise in the coordinate plane but does not produce a dilation.
Answer:
L(z)=(\(\frac{\sqrt{2}}{2}\)-i \(\frac{\sqrt{2}}{2}\))z
c. Find a transformation rx-axis∶C→C that reflects a point represented by the complex number z across the
x-axis.
Answer:
L(z)=\(\overline{\mathbf{Z}}\), the conjugate of z
Discussion
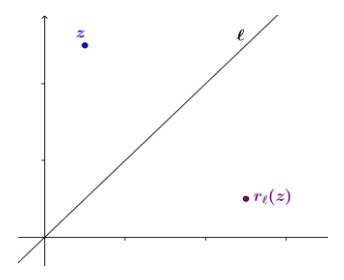
We want to find a transformation rl:C→C that reflects a point representing a complex number z across the diagonal line l with equation y=x.

Recall from Algebra II, Module 3 that the transformation (x,y)→(y,x) accomplishes this reflection across the diagonal line in the coordinate plane, but students are now looking for a formula that produces this result for the complex number x+yi. If students mention this transformation, praise them for making the connection to past work, and ask them to keep this response in mind for verifying the answer they get with the new approach. The steps outlined below demonstrate that the reflection across a line other than the x-axis or y-axis can be accomplished by a sequence of rotations so that the line of reflection aligns with the x-axis, reflects across the x-axis, and rotates so that the line is back in its original position.
Display or reproduce the image above to guide students through this Discussion as they take notes. Ask students to draw a point rl(z) where they think the reflection of z across line l is. Draw it on the teacher version also. Walk through the sequence of transformations geometrically before introducing the analytical formulas.
We know how to find transformations that produce the effect of rotating by a certain amount around the origin, dilating by a certain scale factor, and reflecting across the
x-axis or the y-axis. Which of these transformations help us to reflect across the diagonal line? Allow students to make suggestions or conjectures.
→ How much do we have to rotate around the origin to have line l align with the positive x-axis?
→ We need to rotate -45°.
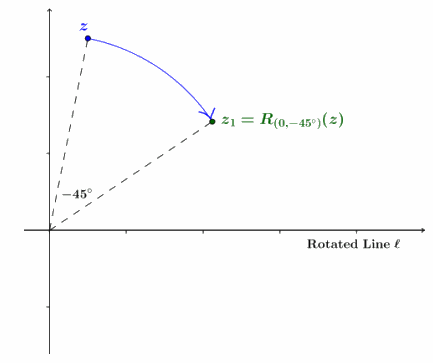
Draw the image of z after rotation by -45° about the origin. Label the new point z1. Give students a quick minute to draw z1 on their version before displaying the teacher version.
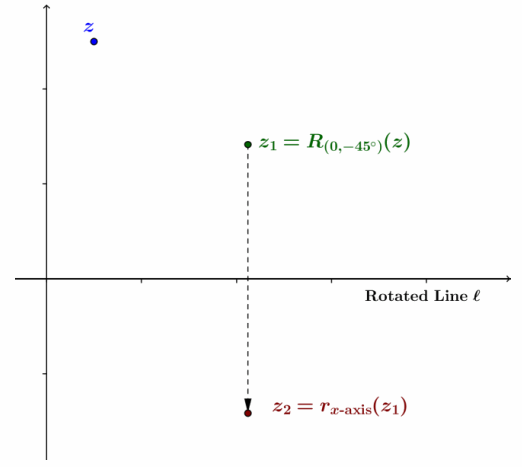
→ Where is the original line l now?
→ It coincides with the positive x-axis.
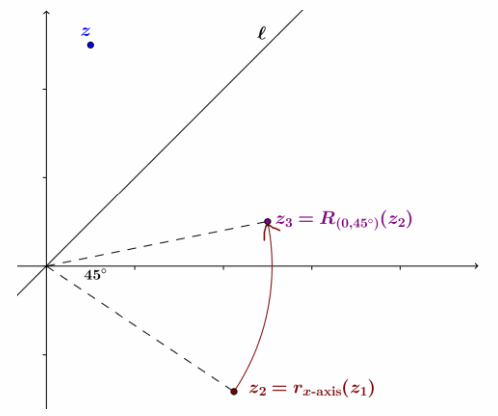
→ We know how to reflect across the x-axis. Draw the reflection of point z1 across the x-axis, and label it z2.
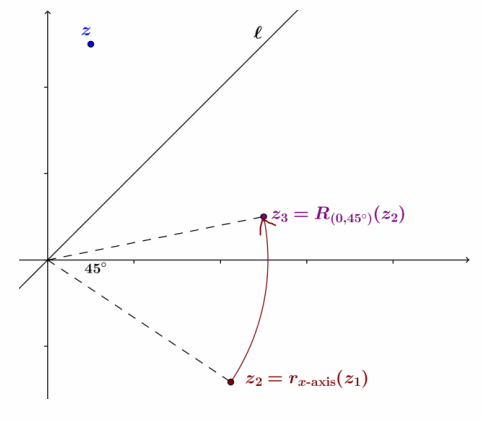
→ Now that we have done a reflection, we need to rotate back to where we started. How much do we have to rotate around the origin to put line l back where it originally was?
→ We need to rotate 45°.
→ Draw the image of z2 under rotation by 45° about the origin. The image should coincide with the original estimate of rl(z).
Now that students have had a chance to think about the geometric steps involved in reflecting z across diagonal line l, repeat the process using the formulas for the three transformations.
→ What is the transformation that accomplishes rotation by -45°? Students answered this question in the Opening Exercise.
→ The transformation is L(z)=(\(\frac{\sqrt{2}}{2}\)-i \(\frac{\sqrt{2}}{2}\))z.
→ We will refer to this transformation using the notation we used in Geometry. We can also factor out the constant \(\frac{\sqrt{2}}{2}\): R(0,-45°)(z)=\(\frac{\sqrt{2}}{2}\)(1-i)z.
→ After we rotate the plane so that line l lies along the x-axis, we reflect the new point z across the x-axis. What is the formula for the transformation rx-axis we use to accomplish the reflection?
→ We use the conjugate of z, so we have rx-axis(z)=\(\bar{Z}\).
→ Now, we can rotate the plane back to its original position by rotating by 45° counterclockwise around the origin. What is the formula for this rotation?
→ From the Opening Exercise, using the notation from Geometry, we have R(0,45°)(z)=\(\frac{\sqrt{2}}{2}\) (1+i)z.
→ We then have
z1=R(0,-45°) (z)=\(\frac{\sqrt{2}}{2}\) (1-i)z
z2=rx-axis(z1)=(\(\overline{z_{1}}\))
z3=R(0,45°)(z2)=\(\frac{\sqrt{2}}{2}\)(1+i) z2.
→ Putting the formulas together, we have
z3= R(0,45°)(z2)
=R(0,45°)(rx-axis(z1))
=R(0,45°)(rx-axis(R(0,-45°)(z))).
Stop here before going forward with the analytic equations, and ensure that all students understand that this formula means that they are first rotating point z by -45° about the origin, then reflecting across the x-axis, and then rotating by 45° about the origin. Remind students that the innermost transformations happen first.
→ Applying the formulas, we have

Then, the transformation rl(z)=i\(\bar{z}\) has the geometric effect of reflection across the diagonal line l with equation y=x.
Exercises
Exercise 1.
The number z in the figure used in the Discussion above is the complex number 1+5i. Compute rl(1+5i), and plot it below.
Answer:
Exercise 2.
We know from previous courses that the reflection of a point (x,y) across the line with equation y=x is the point (y,x). Does this agree with our result from the previous discussion?
Answer:
Yes, we can represent the point (x,y) by z=x+iy. Then,
rl(z)=rl(x+iy)
= i \(\overline{(x+l y)}\)
=i(x-iy)
=y+ix,
which corresponds to the point (y,x).
Exercise 3.
We now want to find a formula for the transformation of reflection across the line l that makes a 60° angle with the positive x-axis. Find formulas to represent each component of the transformation, and use them to find one formula that represents the overall transformation.
Answer:
The transformation consists of rotating line l so that it coincides with the x-axis, reflecting across the x-axis, and rotating the x-axis back to the original position of line l. The components of the transformation can be represented by these formulas:
z1=R(0,-60°)(z)=(\(\frac{1}{2}\)–\(\frac{\sqrt{3}}{2}\)i)z
z2=rx-axis(z1)=(\(\overline{\boldsymbol{z}_{\mathbf{1}}}\))
z3=R(0,60°)(z2) =(\(\frac{1}{2}\)+\(\frac{\sqrt{3}}{2}\)i)z2.
Putting the formulas together, we have
z3= R(0,60°)(z2)
=R(0,60°)(rx-axis(z1))
=R(0,60°)(rx-axis(R(0,-60°)(z))).
Stop here before going forward with the analytic equations, and ensure that all students understand that this formula means that we are first rotating point z by -60° about the origin, then reflecting across the x-axis, and then rotating by 60° about the origin. Remind students that the innermost transformations happen first.
Applying the formulas, we have
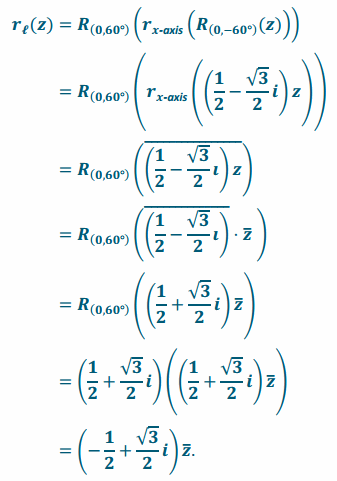
Then, the transformation rl(z)=(-\(\frac{1}{2}\)+\(\frac{\sqrt{3}}{2}\)i)\(\overline{\boldsymbol{Z}}\) has the geometric effect of reflection across the line l that makes a 60° angle with the positive x-axis.
Eureka Math Precalculus Module 1 Lesson 16 Problem Set Answer Key
Question 1.
Find a formula for the transformation of reflection across the line l with equation y=-x.
Answer:
z1=R(0, -135°)(z)=(-\(\frac{\sqrt{2}}{2}\)–\(\frac{\sqrt{2}}{2}\) i)z; if students cannot see it, you can say that:

Question 2.
Find the formula for the sequence of transformations comprising reflection across the line with equation y=x and then rotation by 180° about the origin.
Answer:
z1=R(0, -45°)(z)=(\(\frac{\sqrt{2}}{2}\)–\(\frac{\sqrt{2}}{2}\)i)z
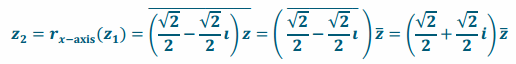
z3=R(0, 45°)(z2)=(\(\frac{\sqrt{2}}{2}\)+\(\frac{\sqrt{2}}{2}\) i)(z2)
z3=R(0,45°)(z2)=(\(\frac{\sqrt{2}}{2}\)+\(\frac{\sqrt{2}}{2}\)i)(z2)=(\(\frac{\sqrt{2}}{2}\)+\(\frac{\sqrt{2}}{2}\) i)(\(\frac{\sqrt{2}}{2}\)+\(\frac{\sqrt{2}}{2}\) i)\(\overline{\mathbf{Z}}\)=i\(\overline{\mathbf{Z}}\)
z4=-z3=-i\(\overline{\mathbf{Z}}\)
Question 3.
Compare your answers to Problems 1 and 2. Explain what you find.
Answer:
They have the same answer/formula that will produce the same transformation of z.
Question 4.
Find a formula for the transformation of reflection across the line l that makes a -30° angle with the positive
x-axis.
Answer:
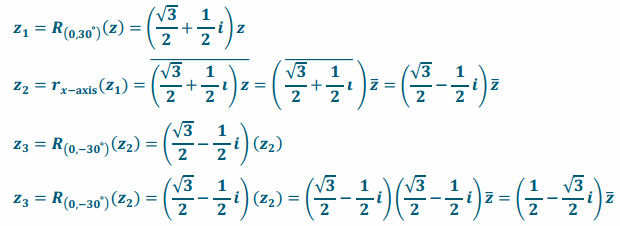
Question 5.
Max observed that when reflecting a complex number, z=a+bi about the line y=x, a and b are reversed, which is similar to how we learned to find an inverse function. Will Max’s observation also be true when the line y=-x is used, where a=-b and b=-a? Give an example to show his assumption is either correct or incorrect.
Answer:
Yes, to reflect a complex number z=a+bi about the line y=-x, we need to do R0,-135°, rx-axis, and then R0, 135°, which will produce the answer to be z=b+ai.
The examples vary. This example will work: z=1+i.
z=a+bi
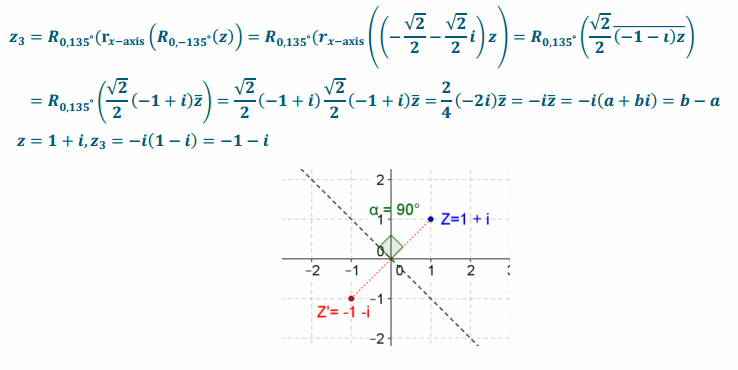
Question 6.
For reflecting a complex number, z=a+bi about the line y=2x, will Max’s idea work if he makes b=2a and a=\(\frac{b}{2}\)? Use z=1+4i as an example to show whether or not it works.
Answer:
No, it will not work based on the example shown. z1=\(\frac{b}{2}\)+2ai=\(\frac{4}{2}\)+2×1i=2+2i Since the angle a≠90°, this is not a reflection.

Question 7.
What would the formula look like if you want to reflect a complex number about the line y=mx, where m>0?
Answer:
For reflecting a complex number or a point about the line going through the origin, we need to know the angle of the line with respect to the positive x-axis to do rotations. So, we can use the slope of the line to find the angle that we need to rotate, which is arctan(m). Now we can come up with a general formula that can be applied to reflecting about the line y=mx, where m>0.
z3=R0,arctan(m)(rx-axis(R0,arctan(-m)(z)),
where R0,arctan(-m)=cos(arctan(-m))+i∙sin(arctan(-m))
R0,arctan(m)=cos(arctan(m))+i∙sin(arctan(m))
Eureka Math Precalculus Module 1 Lesson 16 Exit Ticket Answer Key
Explain the process used in the lesson to locate the reflection of a point z across the diagonal line with equation y=x. Include figures in your explanation.
Answer:
First, we rotated the point z by -45° to align the diagonal line with equation y=x with the x-axis to get a new point z1.
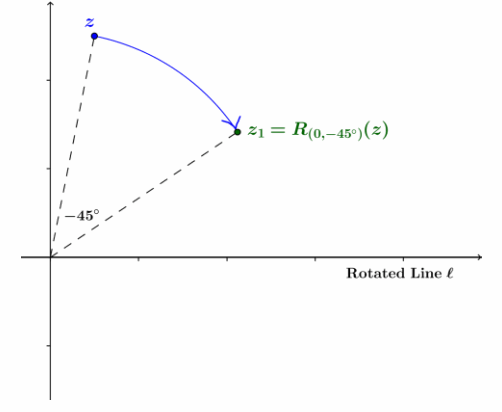
Then, we reflected the point z1 across the real axis to find point z2.
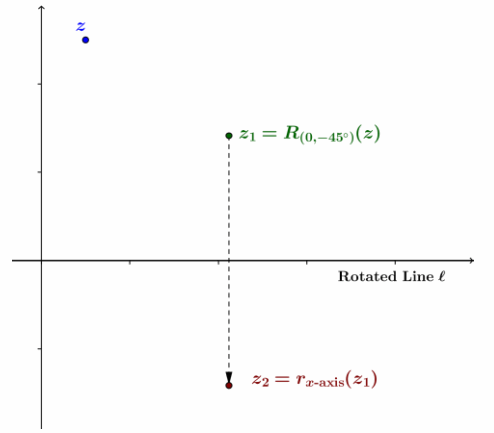
Finally, we rotated everything back by 45° to find the final point z3=rl(z).