Engage NY Eureka Math Precalculus Module 1 Lesson 12 Answer Key
Eureka Math Precalculus Module 1 Lesson 12 Exercise Answer Key
Opening Exercise
a. Let A=2+3i and B=-4-8i. Find a complex number C so that B is the midpoint of A and C.
Answer:
C=-10-19i
b. Given two complex numbers A and B, find a formula for a complex number C in terms of A and B so that B is the midpoint of A and C.
Answer:
C=2B-A
c. Verify that your formula is correct by using the result of part (a).
Answer:
C=2B-A
-10-19i=2(-4-8i)-(2+3i)
=-8-16i-2-3i
=-10-19i
Exercise 1.
Let z=-100+100i and w=1000-1000i.
a. Find a point one-quarter of the way along the line segment connecting z and w closer to z than to w.
Answer:
Let M be the midpoint between z and w=450-450i.
Let M’ be the midpoint between z and M=175-175i.
The complex number 175-175i represents a point on the complex plane that is one-quarter of the way from z on the segment connecting z and w.
b. Write this point in the form αz+βw for some real numbers α and β. Verify that this does in fact represent the point found in part (a).
Answer:
\(\frac{3}{4}\)z+\(\frac{1}{4}\)w=\(\frac{3}{4}\)(-100+100i)+\(\frac{1}{4}\)(1000-1000i)
=(-75+250)+i(75-250)
=175-175i
c. Describe the location of the point \(\frac{2}{5}\)z+\(\frac{3}{5}\)w on this line segment.
Answer:
This point is located \(\frac{3}{5}\)of the way from z and \(\frac{2}{5}\)of the way from w on \(\overline{\boldsymbol{Z W}}\).
Eureka Math Precalculus Module 1 Lesson 12 Exploratory Challenge Answer Key

a. Draw three points A, B, and C in the plane.
b. Start at any position P0, and leapfrog over A to a new position P1 so that A is the midpoint of \(\overline{P_{0} P_{1}}\).
c. From P1, leapfrog over B to a new position P2 so that B is the midpoint \(\overline{P_{1} P_{2}}\).
d. From P2, leapfrog over C to a new position P3 so that C is the midpoint \(\overline{P_{2} P_{3}}\).
e. Continue alternately leapfrogging over A, then B, and then C.
f. What eventually happens?
Answer:
At the sixth jump, you end up at the initial point P6=P0.
g. Using the formula from the Opening Exercise, part (b), show why this happens.
Answer:
P1=2A-P0
P2=2B-P1=2B-2A+P0
P3=2C-P2=2C-2B+2A-P0
P4=2A-P3=-2C+2B+P0
P5=2B- P4=2C-P0
P6=2C-P5=P0
→ What happened on the sixth jump?
→ We landed back at the starting point. (Note: Allow a couple of groups to share their graph. A sample is provided.)
Exploratory Challenge 2
a. Plot a single point A in the plane.
b. What happens when you repeatedly jump over A?
Answer:
You keep alternating between landing on P0 and landing on P1.
c. Using the formula from the Opening Exercise, part (b), show why this happens.
Answer:
P1=2A-P0
P2=2A- P1=2A- 2A+P0=P0
d. Make a conjecture about what will happen if you leapfrog over two points, A and B, in the coordinate plane.
Answer:
Answers will vary.
e. Test your conjecture by using the formula from the Opening Exercise, part (b).
Answer:
Answers will vary.
f. Was your conjecture correct? If not, what is your new conjecture about what happens when you leapfrog over two points, A and B, in the coordinate plane?
Answer:
Answers will vary, but for the most part, students should have found that their conjecture was incorrect. In this game, you never return to the starting position. Instead, the points continue to get farther away from points A and B. This can be seen by using the formula from the Opening Exercise, part (b).
g. Test your conjecture by actually conducting the experiment.
Eureka Math Precalculus Module 1 Lesson 12 Problem Set Answer Key
Question 1.
Find the distance between the following points.
a. Point A(2,3) and point B(6,6)
Answer:
AB=\(\sqrt{(2-6)^{2}+(3-6)^{2}}\)
=\(\sqrt{16+9}\)
=5
b. A=2+3i and B=6+6i
Answer:
|A-B|=|2+3i-6-6i|
=|-4-3i|
=\(\sqrt{(-4)^{2}+(-3)^{2}}\)
=\(\sqrt{16+9}\)
=5
c. A=-1+5i and B=5+11i
Answer:
|A-B|=|-1+5i-5-11i|
=|-6-6i|
=\(\sqrt{(-6)^{2}+(-6)^{2}}\)
=\(\sqrt{2(6)^{2}}\)
=\(6 \sqrt{2}\)
d. A=1-2i and B=-2+3i
Answer:
|A-B|=|1-2i+2-3i|
=|3-5i|
=\(\sqrt{(3)^{2}+(-5)^{2}}\)
=\(\sqrt{9+25}\)
=\(\sqrt{34}\)
e. A=\(\frac{1}{2}\)–\(\frac{1}{2}\)i and B=-\(\frac{2}{3}\)+\(\frac{1}{3}\) i
Answer:
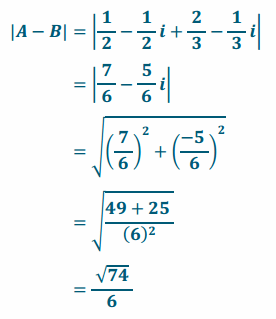
Question 2.
Given three points A, B, C, where C is the midpoint of A and B.
a. If A=-5+2i and C=3+4i, find B.
Answer:
C=\(\frac{A+B}{2}\)
B=2C-A
=2(3+4i)-(-5+2i)
=6+8i+5-2i
=11+6i
b. If B=1+11i and C=-5+3i, find A.
Answer:
C=\(\frac{\boldsymbol{A}+\boldsymbol{B}}{2}\)
A=2C-B
=2(-5+3i)-(1+11i)
=-10+6i-1-11i
=-11-5i
Question 3.
Point C is the midpoint between A=4+3i and B=-6-5i. Find the distance between points C and D for each point D provided below.
a. 2D=-6+8i
Answer:
C=\(\frac{4-6}{2}\)+\(\frac{3-5}{2}\)i=-1-i
D=-3+4i
|C-D|=|-1-i+3-4i|
=|-2-5i|
=\(\sqrt{(-2)^{2}+(5)^{2}}\)
=\(\sqrt{29}\)
b. D=-\(\overline{\boldsymbol{B}}\)
Answer:
D=6-5i
|C-D|=|-1-i-6+5i|
=|-7+4i|
=\(\sqrt{(-7)^{2}+(4)^{2}}\)
=\(\sqrt{65}\)
Question 4.
The distance between points A=1+1i and B=a+bi is 5. Find the point B for each value provided below.
a. a=4
Answer:
5=\(\sqrt{(1-4)^{2}+(1-b)^{2}}\)
25=9+(1-b)2
1-b=±4
b=-3,5
B=4-3i or B=4+5i
b. b=6
Answer:
5=\(\sqrt{(1-a)^{2}+(1-6)^{2}}\)
25=(1-a)2+25
(1-a)2=0
1-a=0
a=1
B=1+6i
Question 5.
Draw five points in the plane A, B, C, D, E. Start at any position, P0, and leapfrog over A to a new position, P1(so, A is the midpoint of (\(\overline{P_{0} P_{1}}\)). Then, leapfrog over B, then C, then D, then E, then A, then B, then C, then D, then E, then A again, and so on. How many jumps will it take to get back to the starting position, P0?
Answer:
It takes 10 jumps to return to the starting position.
P1=2A-P0
P2=2B-P1=2B-2A+P0
P3=2C-P2=2C-2B+2A-P0
P4=2D-P3=2D-2C+2B-2A+P0
P5=2E-P4=2E-2D+2C-2B+2A-P0
P6=2A-P5=2A-2E+2D-2C+2B-2A+P0=-2E+2D-2C+2B+P0
P7=2B-P6=2B+2E-2D+2C-2B-P0=2E-2D+2C-P0
P8=2C-P7=2C-2E+2D-2C+P0=-2E+2D+P0
P9=2D-P8=2D+2E-2D-P0=2E-P0
P10=2E-P9=2E-2E+P0=P0
Question 6.
For the leapfrog puzzle problems in both Exploratory Challenge 1 and Problem 5, we are given an odd number of points to leapfrog over. What if we leapfrog over an even number of points? Let A=2, B=2+i, and P0=i. Will Pn ever return to the starting position, P0? Explain how you know.
Answer:
No, we cannot get back to the starting position. For example, if we leapfrog over two given even points, A and B.
P1=2A-P0
P2=2B-P1=2B-2A+P0
P3=2A-P2=2A-2B+2A-P0=4A-2B-P0
P4=2B-P3=2B-4A+2B+P0=4B-4A+P0
P5=2A-P4=2A-4B+4A-P0=6A-4B-P0
If n is even, Pn=nB-nA+P0=n(B-A)+ P0. Then, if P0=Pn, we have 0=n(B-A), which would mean that B=A, which we know to be false. Thus, for even values of n, Pn will never return to P0.
If n is odd, Pn=(n+1)A-(n-1)B-P0. Then, if P0=Pn we have
2P0=(n+1)A-(n-1)B
=(n+1)2-(n-1)(2+i)
=-4-(n-1)i
2i=-4-(n-1)i
(n+1)i=-4.
Since (n+1)i is an imaginary number and -4 is a real number, it is impossible for (n+1)i to equal -4. Thus, for odd values of n, Pn will never return to P0.
Therefore, it is not possible for Pn to ever coincide with P0 for these values of A, B, and P0.
Eureka Math Precalculus Module 1 Lesson 12 Exit Ticket Answer Key
Question 1.
Find the distance between the following points.
a. (4,-9) and (1,-5)
Answer:
AB=\(\sqrt{(4-1)^{2}+(-9+5)^{2}}\)
=\(\sqrt{9+16}\)
=5
b. A=4-9i and B=1-5i
Answer:
|A-B|=|4-9i-1+5i|
=|3-4i|
=\(\sqrt{(3)^{2}+(-4)^{2}}\)
=\(\sqrt{25}\)
=5
c. Explain why they have the same answer numerically in parts (a) and (b) but a different perspective in geometric effect
Answer:
The length of the line segment connecting points A and B is 5.
To find the distance between two complex numbers A and B, we need to calculate A-B=4-9i-1+5i, which has the geometric effect of performing a translation—shifting one unit to the left and 5 units upward from point A=4-9i. The result is 3-4i. And |3-4i| is the distance from the origin to the complex number -4i, which is not exactly the same as \(\overline{\boldsymbol{AB}}\) in terms of their position. However, they all have the same numerical value in terms of distance, which is 5.
Question 2.
Given point A=3-2i and point M=-2+i, if M is the midpoint of A and another point B, find the coordinates of point B.
Answer:
-2+i=\(\frac{(3-2 i)+M}{2}\)
-4+2i=3-2i+M
-7+4i=M