Engage NY Eureka Math 8th Grade Module 5 End of Module Assessment Answer Key
Eureka Math Grade 8 Module 5 End of Module Assessment Task Answer Key
Question 1.
a. We define x as a year between 2008 and 2013 and y as the total number of smartphones sold that year, in millions. The table shows values of x and corresponding y values.

i) How many smartphones were sold in 2009?
Answer:
17.3 Million Smartphones were sold in 2009
ii) In which year were 90 million smartphones sold?
Answer:
90 Million Smartphones were sold in 2011
iii) Is y a function of x? Explain why or why not.
Answer:
Yes, It is a function because for each input there is exactly one output. Specifically only one number will be assigned to represent the number of smartphones sold in the given year.
b. Randy began completing the table below to represent a particular linear function. Write an equation to represent the function he was using and complete the table for him.

Answer:

y = 3x + 4
c. Create the graph of the function in part (b).
Answer:
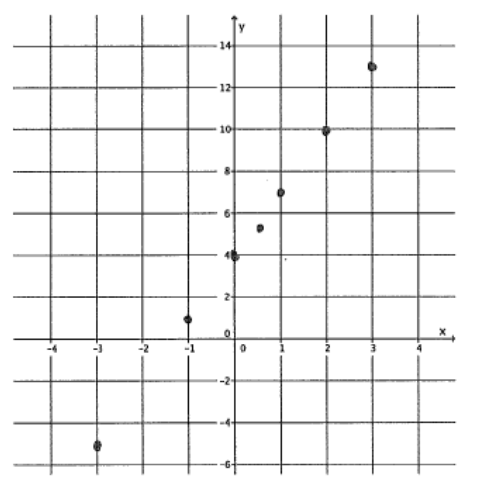
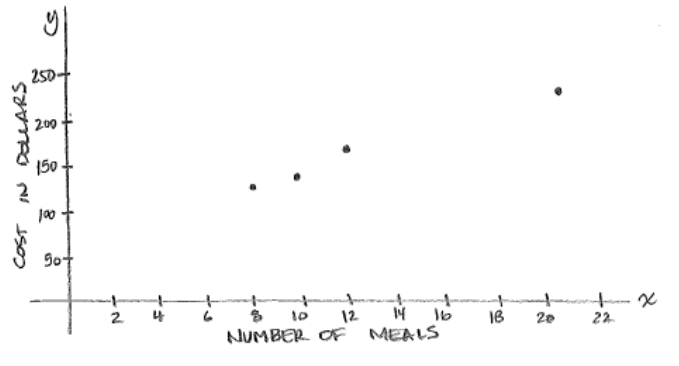
d. At NYU in 2013, the cost of the weekly meal plan options could be described as a function of the number of meals. Is the cost of the meal plan a linear or nonlinear function? Explain.
8 meals: $125/week
10 meals: $135/week
12 meals: $155/week
21 meals: $220/week
Answer:
\(\frac{125}{8}\) = 15.625
\(\frac{135}{10}\) = 13.5
\(\frac{155}{12}\) = 12.917
\(\frac{220}{21}\) = 10.476
The cost of the meal plan is a nonlinear function. The cost per meal is different based on the plan. Chosen for example, one plan charges almost $16 per meal while another is about $10. Also, when the data is graphed, The points do not fall on a line.
Question 2.
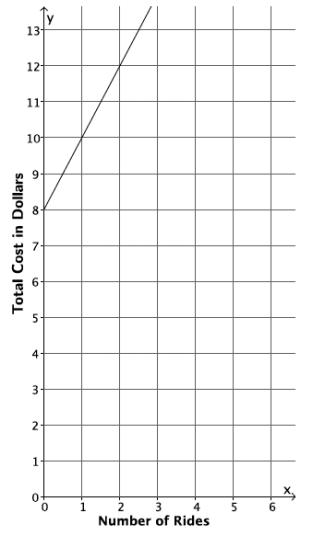
The cost to enter and go on rides at a local water park, Wally’s Water World, is shown in the graph below.
A new water park, Tony’s Tidal Takeover, just opened. You have not heard anything specific about how much it costs to go to this park, but some of your friends have told you what they spent. The information is organized in the table below.

Each park charges a different admission fee and a different fee per ride, but the cost of each ride remains the same.
a. If you only have $14 to spend, which park would you attend (assume the rides are the same quality)? Explain.
Answer:
Let x represent the number of rides
Let w represent the total cost at wally’s water world
W = 2x + 8
Wally’s
W = 2x + 8
14 = 2x + 8
6 = 2x
3 = x
Tony’s
T = 0.75x + 12
14 = 0.75x + 12
2 = 0.75x
2.67 ≈ x
At wally’s you can go in 3 rides with $14, At tony’s just 2 rides. I would go to wally’s because i could go on more rides.
b. Another water park, Splash, opens, and they charge an admission fee of $30 with no additional fee for rides. At what number of rides does it become more expensive to go to Wally’s Water World than Splash? At what number of rides does it become more expensive to go to Tony’s Tidal Takeover than Splash?
Answer:
Let S represent total cost at splash, S = 30
Wally’s
30 = 2x + 8
22 = 2x
11 = x
Tony’s
30 = 0.75x + 12
18 = 0.75x
24 = x
At Wally’s you can go on 11 rides with $30. The 12th ride makes wally’s more expensive than splash.
At Tony’s you can go on 24 rides with $30. The 25th ride makes tony’s more expensive than splash.
c. For all three water parks, the cost is a function of the number of rides. Compare the functions for all three water parks in terms of their rate of change. Describe the impact it has on the total cost of attending each park.
Answer:
Wally’s rate of change is 2, $2 per ride.
Tony’s rate of change is 0.75, $0.75 per ride.
Splash’s rate of change is 0, $0 extra per ride.
Wally’s has the greatest rate of change that means that the total cost at wally’s will increase the fastest as we go on more rides. At tony’s the rate of change is just 0.75 so the total cost increases with the number of rides we go on, but not as quickly as wally’s. Splash has a rate of change of zero, The number of rides we go on does not impact the total cost at all.
Question 3.
For each part below, leave your answers in terms of π.
a. Determine the volume for each three-dimensional figure shown below.

Answer:
V = \(\frac{1}{3}\) π (16)(9)
= (16)(3)π
= 48 π
The volume is 48 π mm2
V = π (4)(5.3)
= π (21.2)
= 21.2 π
The volume is 21.2 π cm3.
V = \(\frac{4}{3}\) π (32)
= 4(9) π
= 36 π
The volume is 36 πin3
b. You want to fill the cylinder shown below with water. All you have is a container shaped like a cone with a radius of 3 inches and a height of 5 inches; you can use this cone-shaped container to take water from a faucet and fill the cylinder. How many cones will it take to fill the cylinder?
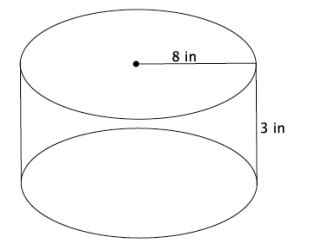
Answer:
Volume of cylinder = π (64) (3)
= 192 π
Volume of cone = \(\frac{1}{3}\) π (9) (5)
= \(\frac{45}{3}\) π
= 15 π
The volume of cylinder is 192 π in3
The volume of cone is 15 π in3
\(\frac{192 \pi}{15 \pi}\) = \(\frac{192}{15}\) = 12.8
It takes 12.8 cone of the given size to fill the cylinder.
c. You have a cylinder with a diameter of 15 inches and height of 12 inches. What is the volume of the largest sphere that will fit inside of it?
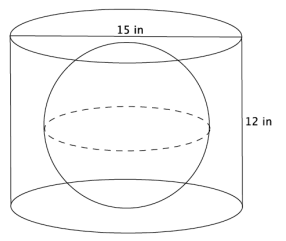
Answer:
The cylinder has radius of 7.5 cm, but the height is just 12 cm. That means the maximum radius for the sphere is 6 cm. Anything larger would not fit in the cylinder. Then the volume of the largest sphere that will fit in the cylinder is 288 in3.
V= \(\frac{4}{3}\) π (63)
= \(\frac{4}{3}\) π (216)
= 288 π