Engage NY Eureka Math 8th Grade Module 4 Mid Module Assessment Answer Key
Eureka Math Grade 8 Module 4 Mid Module Assessment Task Answer Key
Question 1.
Write and solve each of the following linear equations.
a. Ofelia has a certain amount of money. If she spends $12, then she has \(\frac{1}{5}\) of the original amount left. How much money did Ofelia have originally?
Answer:
Let x be the amount of money ofelia had
x – 12 = \(\frac{1}{5}\)
x – \(\frac{1}{5}\)x – 12 + 12 = \(\frac{1}{5}\) x – \(\frac{1}{5}\) x +12
\(\frac{4}{5}\) x = 12
x= 12 ∙ \(\frac{5}{4}\) = \(\frac{60}{4}\)
Ofelia had $15.00 originally.
b. Three consecutive integers have a sum of 234. What are the three integers?
Answer:
Let x be the first integer
x + x + 1 + x + 2 = 234
3x + 3 = 234
3x = 234 – 3
3x = 231
x = 77
The integers are 77, 78, and 79
c. Gil is reading a book that has 276 pages. He already read some of it last week. He plans to read 20 pages tomorrow. By then, he will be \(\frac{2}{3}\)of the way through the book. How many pages did Gil read last week?
Answer:
Let x be the number of pages gil read last week.
x + 20 = \(\frac{2}{3}\)(276)
x + 20 = 184
x + 20 – 20 = 184 – 20
x = 164
Gil read 164 pages last week
Question 2.
a. Without solving, identify whether each of the following equations has a unique solution, no solution,
or infinitely many solutions.
i. 3x + 5 = – 2
Answer:
Unique
ii. 6(x – 11) = 15 – 4x
Answer:
Unique
iii. 12x + 9 = 8x + 1 + 4x
Answer:
No solution
iv. 2(x – 3) = 10x – 6 – 8x
Answer:
Infinitely many solutions
v. 5x + 6 = 5x – 4
Answer:
No solution
b. Solve the following equation for a number x. Verify that your solution is correct.
– 15 = 8x + 1
Answer:
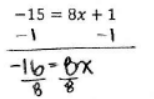
-2 = x
-15 = 8(-2) + 1
-15 = -16 + 1
-15 = -15
c. Solve the following equation for a number x. Verify that your solution is correct.
7(2x + 5) = 4x – 9 – x
Answer:
7(2x + 5) = 4x – 9 – x
14x + 35 = 4x – 9 – x
14x + 35 = 3x – 9
14x – 3x + 35 = 3x – 3x – 9
11x + 35 = -9
11x + 35 – 35 = -9 – 35
11x = -44
x = -4
7(2(-4) + 5) = 4(-4) – 9 – (-4)
7(-8 + 5) = -16 – 9 + 4
7(-3) = -25 + 4
-21 = -21
Question 3.
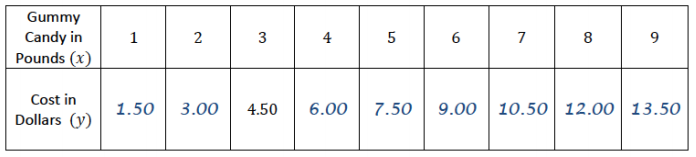
a. Parker paid $4.50 for three pounds of gummy candy. Assuming each pound of gummy candy costs the same amount, complete the table of values representing the cost of gummy candy in pounds.
Answer:
b. Graph the data on the coordinate plane.
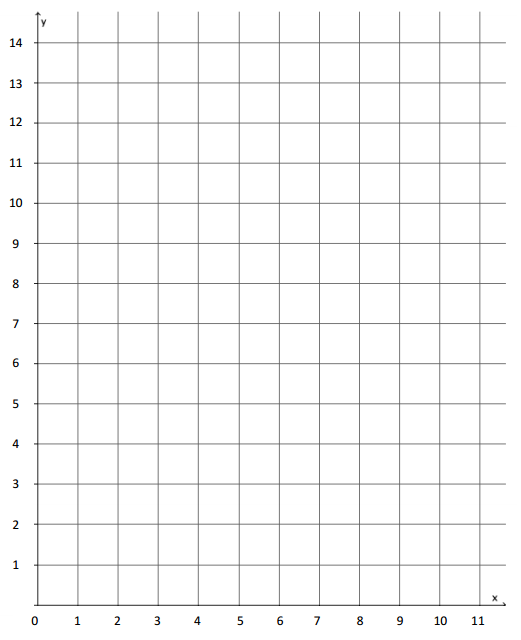
Answer:
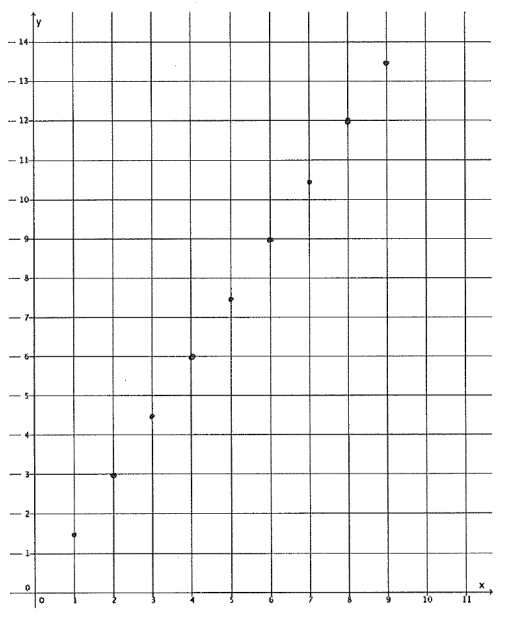
c. On the same day, Parker’s friend, Peggy, was charged $5 for 1 \(\frac{1}{2}\) lb. of gummy candy. Explain in terms of the graph why this must be a mistake.
Answer:
Even though 1\(\frac{1}{2}\) pounds of candy isn’t a point on the graph, it is reasonable to believe it will fall in line with the other points. The cost of 1\(\frac{1}{2}\) pounds of candy does not fit the pattern.