Eureka Math Grade 8 Module 3 Lesson 13 Answer Key

Engage NY Eureka Math 8th Grade Module 3 Lesson 13 Answer Key

Eureka Math Grade 8 Module 3 Lesson 13 Exercise Answer Key

Exercises
Use the Pythagorean theorem to determine the unknown length of the right triangle.

Exercise 1.
Determine the length of side c in each of the triangles below.

a.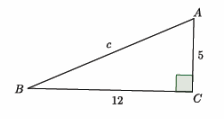
Answer:
5²+12²=c²
25+144=c²
169=c²
13=c

b.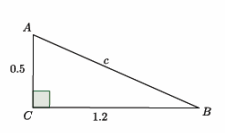
Answer:
0.5²+1.2²=c²
0.25+1.44=c²
1.69=c²
1.3=c

Exercise 2.
Determine the length of side b in each of the triangles below.
a.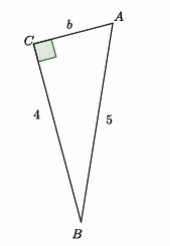
Answer:
4²+b²=5²
16+b²=25
16-16+b²=25-16
b²=9
b=3

b.
Answer:
0.4²+b²=0.5²
0.16+b²=0.25
0.16-0.16+b²=0.25-0.16
b²=0.09
b=0.3

Exercise 3.
Determine the length of \(\overline{Q S}\). (Hint: Use the Pythagorean theorem twice.)

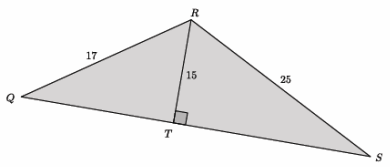
Answer:
15²+|QT|²=17²
225+|QT|²=289
225-225+|QT|²=289-225
|QT|²=64
|QT| = 8

15²+|TS|²=25²
225+|TS|²=625
225-225+|TS|²=625-225
|TS|²=400
|TS|=20
Since |QT|+|TS|=|QS|, then the length of side \(\overline{Q S}\) is 8+20, which is 28.

Eureka Math Grade 8 Module 3 Lesson 13 Exit Ticket Answer Key

Determine the length of side \(\overline{B D}\) in the triangle below.

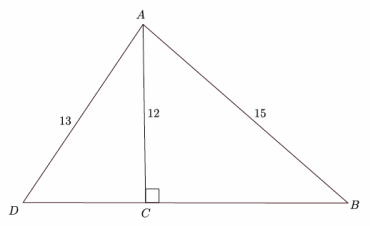
Answer:
First, determine the length of side \(\overline{B C}\).
12²+BC²=15²
144+BC²=225
BC²=225-144
BC²=81
BC=9

Then, determine the length of side \(\overline{C D}\).
12²+CD²=13²
144+CD²=169
CD²=169-144
CD²=25
CD=5
Adding the lengths of sides \(\overline{B C}\) and \(\overline{C D}\) determines the length of side \(\overline{B D}\); therefore, 5+9=14. \(\overline{B D}\) has a length of 14.

Eureka Math Grade 8 Module 3 Lesson 13 Problem Set Answer Key

Students practice using the Pythagorean theorem to find unknown lengths of right triangles.

Use the Pythagorean theorem to determine the unknown length of the right triangle.

Question 1.
Determine the length of side c in each of the triangles below.
a.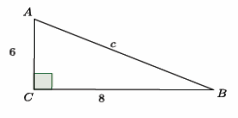
Answer:
6²+8²=c²
36+64=c²
100=c²
10=c

b.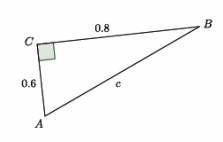
Answer:
0.6²+0.8²=c²
0.36+0.64=c²
1=c²
1=c

Question 2.
Determine the length of side a in each of the triangles below.
a.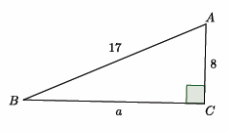
Answer:
a²+8²=17²
a²+64=289
a²+64-64=289-64
a²=225
a=15

b.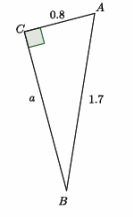
Answer:
a²+0.8²=1.7²
a²+0.64=2.89
a²+0.64-0.64=2.89-0.64
a²=2.25
a=1.5

Question 3.
Determine the length of side b in each of the triangles below.
a.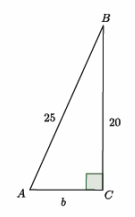
Answer:
20²+b²=25²
400+b²=625
400-400+b²=625-400
b²=225
b=15

b.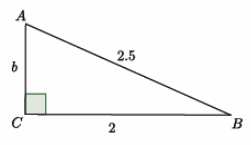
Answer:
2²+b²=2.5²
4+b²=6.25
4-4+b²=6.25-4
b²=2.25
b=1.5

Question 4.
Determine the length of side a in each of the triangles below.
a.
Answer:
a²+12²=20²
a²+144=400
a²+144-144=400-144
a²=256
a=16

b.
Answer:
a²+1.2²=2²
a²+1.44=4
a²+1.44-1.44=4-1.44
a²=2.56
a=1.6

Question 5.
What did you notice in each of the pairs of Problems 1–4? How might what you noticed be helpful in solving problems like these?
Answer:
In each pair of problems, the problems and solutions were similar. For example, in Problem 1, part (a) showed the sides of the triangle were 6, 8, and 10, and in part (b), they were 0.6, 0.8, and 1. The side lengths in part (b) were a tenth of the value of the lengths in part (a). The same could be said about parts (a) and (b) of Problems 2–4. This might be helpful for solving problems in the future. If I am given side lengths that are decimals, then I could multiply them by a factor of 10 to make whole numbers, which are easier to work with. Also, if I know common numbers that satisfy the Pythagorean theorem, like side lengths of 3, 4, and 5, then I recognize them more easily in their decimal forms, that is, 0.3, 0.4, and 0.5.