Eureka Math Grade 8 Module 1 Lesson 3 Answer Key

Engage NY Eureka Math 8th Grade Module 1 Lesson 3 Answer Key

Eureka Math Grade 8 Module 1 Lesson 3 Example Answer Key

Examples 1–2
Work through Examples 1 and 2 in the same manner. (Supplement with additional examples if needed.) Have students calculate the resulting exponent; however, emphasis should be placed on the step leading to the resulting exponent, which is the product of the exponents.
Example 1.
(7² )⁶=
Answer:

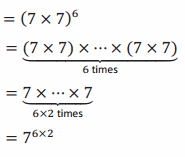
Example 2.
(1.3)³ )¹⁰=
Answer:
(1.3×1.3×1.3)¹⁰

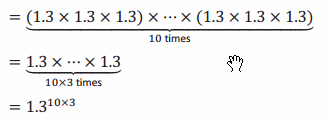
Eureka Math Grade 8 Module 1 Lesson 3 Exercise Answer Key

Exercise 1.
(15³)⁹=
Answer:
(15)^9×3

Exercise 2.
((-2)⁵ )⁸=
Answer:
(-2)^8×5

Exercise 3.
(3.4¹⁷)⁴=
Answer:
3.4^4×17

Exercise 4.
Let s be a number.
Answer:
(s¹⁷ )⁴=
Answer:
s^4×17

Exercise 5.
Sarah wrote (3⁵ )⁷=3¹². Correct her mistake. Write an exponential expression using a base of 3 and exponents of 5, 7, and 12 that would make her answer correct.
Answer:
Correct way: (3⁵ )⁷=3³⁵; Rewritten Problem: 3⁵×3⁷=3⁵⁺⁷=3¹².

Exercise 6.
A number y satisfies y²⁴-256=0. What equation does the number x=y⁴ satisfy?
Answer:
Since x=y⁴, then (x)⁶=(y⁴ )⁶. Therefore, x=y⁴ would satisfy the equation x⁶-256=0.

Exercises 7–13 (10 minutes)
Have students complete Exercises 17–12 independently and then check their answers.

Exercise 7.
(11×4)⁹=
Answer:
11^9×1×4^9×1

Exercise 8.
(3²×7⁴ )⁵=
Ans:
3^5×2×7^5×4

Exercise 9.
Let a, b, and c be numbers.
(3² a⁴ )⁵=
Answer:
3^5×2 a^5×4

Exercise 10.
Let x be a number.
(5x)⁷=
Ans:
5^7×1 ∙x^7×1

Exercise 11.
Let x and y be numbers.
(5xy² )⁷=
Ans:
5^7×1 ∙x^7×1∙y^7×2

Exercise 12.
Let a, b, and c be numbers.
(a² bc³ )⁴=
Ans:
a^4×2 ∙b^4×1∙c^4×3

Exercise 13.
Let x and y be numbers, y≠0, and let n be a positive integer. How is (\(\frac{x}{y}\))ⁿ related to xⁿ and yⁿ?
Answer:
(\(\frac{x}{y}\))ⁿ=\(\frac{x^{n}}{y^{n}}\)
Because

Eureka Math Grade 8 Module 1 Lesson 3 Problem Set Answer Key

Question 1.
Show (prove) in detail why (2∙3∙7)⁴=2⁴ 3⁴ 7⁴.
Answer:
(2∙3∙7)⁴=(2∙3∙7)(2∙3∙7)(2∙3∙7)(2∙3∙7)
=(2∙2∙2∙2)(3∙3∙3∙3)(7∙7∙7∙7)
By repeated use of the commutative and associative properties
=2⁴ 3⁴ 7⁴ By definition

Question 2.
Show (prove) in detail why (xyz)⁴=x⁴ y⁴ z⁴ for any numbers x,y,z.
Answer:
The left side of the equation (xyz)⁴ means (xyz) (xyz) (xyz) (xyz). Using the commutative and associative properties of multiplication, we can write (xyz) (xyz) (xyz) (xyz) as (xxxx)(yyyy) (zzzz), which in turn can be written as x⁴ y⁴ z⁴, which is what the right side of the equation states.

Question 3.
Show (prove) in detail why (xyz)ⁿ=xⁿ yⁿ zⁿ for any numbers x, y, and z and for any positive integer n.
Ans:
Beginning with the left side of the equation, (xyz)ⁿ means . Using the commutative and associative properties of multiplication, can be rewritten as and, finally, xⁿ yⁿ zⁿ, which is what the right side of the equation states. We can also prove this equality by a different method, as follows. Beginning with the right side xⁿ yⁿ zⁿ means which by the commutative property of multiplication can be rewritten as . Using exponential notation, 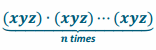can be rewritten as (xyz)ⁿ, which is what the left side of the equation states.

Eureka Math Grade 8 Module 1 Lesson 3 Exit Ticket Answer Key

Write each expression as a base raised to a power or as the product of bases raised to powers that is equivalent to the given expression.

Question 1.
(9³ )⁶=
Ans:
(9³ )⁶=9^6×3=9¹⁸

Question 2.
(113²×37×51⁴ )³=
Ans:
(113²×37×51⁴ )³=((113²×37)×51⁴ )³ By associative law
= (113²×37)³×(51⁴ )³ Because (xy)ⁿ=xⁿ yⁿ for all numbers x, y
= (113²)³×37³×(51⁴)³ Because (xy)ⁿ=xⁿ yⁿ for all numbers x, y
= 113⁶×37³×51¹² Because (x^m)ⁿ=x^mn for all numbers x

Question 3.
Let x,y,z be numbers. (x² yz⁴ )³=
Answer:
(x²yz⁴ )³=((x²×y)×z⁴ )³ By associative law
= (x²×y)³×(z⁴ )³ Because (xy)ⁿ=xⁿ yⁿ for all numbers x, y
=(x² )³×y³×(z⁴ )³ Because (xy)ⁿ=xⁿ yⁿ for all numbers x, y
=x⁶×y³×z¹² Because (x^m)ⁿ=x^mn for all numbers x
= x⁶ y³ z¹²

Question 4.
Let x,y,z be numbers and let m,n,p,q be positive integers. (x^m yⁿ z^p)^q=
Ans:
(x^m yⁿ z^p )^q=((x^m×yⁿ )×z^p)^q By associative law
=(x^m×yⁿ )^q×(z^p )^q Because (xy)ⁿ=xⁿ yⁿ for all numbers x, y
=(x^m )^q×(yⁿ )^q×(z^p)^q Because (xy)ⁿ=xⁿ yⁿ for all numbers x, y
= x^mp×y^nq×z^pq Because (x^m )ⁿ=x^mn for all numbers x
=x^mqy^nqz^pq

Question 5.
\(\frac{4^{8}}{5^{8}}\) =
Answer:
\(\frac{4^{8}}{5^{8}}\) = \(\left(\frac{4}{5}\right)^{8}\)