Engage NY Eureka Math 8th Grade Module 1 End of Module Assessment Answer Key
Eureka Math Grade 8 Module 1 End of Module Assessment Task Answer Key
Question 1.
You have been hired by a company to write a report on Internet companies’ Wi-Fi ranges. They have requested that all values be reported in feet using scientific notation.
Ivan’s Internet Company boasts that its wireless access points have the greatest range. The company claims that you can access its signal up to 2,640 feet from its device. A competing company, Winnie’s Wi-Fi, has devices that extend to up to 2\(\frac{1}{2}\) miles.
a. Rewrite the range of each company’s wireless access devices in feet using scientific notation, and state which company actually has the greater range (5,280 feet =1 mile).
Answer:
Ivan’s Range: 2,640 = 2.64 × 103 ft.
Winner’s Range: (2.5)5280 = 13200 = 1.32 × 104 ft.
Winner’s wi-fi has the greater range.
b. You can determine how many times greater the range of one Internet company is than the other by writing their ranges as a ratio. Write and find the value of the ratio that compares the range of Winnie’s wireless access devices to the range of Ivan’s wireless access devices. Write a complete sentence describing how many times greater Winnie’s Wi-Fi range is than Ivan’s Wi-Fi range.
Answer:
winnie to ivan’s ratio – (1.32 × 104) : (2.64 × 103)
Value of ratio – \(\frac{1.32 \times 10^{4}}{2.64 \times 10^{3}}\) = \(\frac{1.32}{2.64}\) × \(\frac{10^{4}}{10^{3}}\) = \(\frac{1}{2}\) × 10 = 5
winnie’s wi-fi is 5 times greater in range than ivan’s internet company.
c. UC Berkeley uses Wi-Fi over Long Distances (WiLD) to create long-distance, point-to-point links. UC Berkeley claims that connections can be made up to 10 miles away from its device. Write and find the value of the ratio that compares the range of Ivan’s wireless access devices to the range of Berkeley’s WiLD devices. Write your answer in a complete sentence.
Answer:
(10)5280 = 52800 = 5.28 × 104
Ivan’s to berkeley ratio: (2.64 × 103): (5.28 × 104)
Value of ratio- \(\frac{2.64 \times 10^{3}}{5.28 \times 10^{4}}\) = \(\frac{2.64}{5.28}\)×\(\frac{10^{3}}{10^{4}}\)= \(\frac{1}{2}\)×\(\frac{1}{10}\)= \(\frac{1}{20}\)
Ivan’s internet devices have a range \(\frac{1}{20}\) the range of UC Berkeley wild devices.
Question 2.
There is still controversy about whether or not Pluto should be considered a planet. Although planets are mainly defined by their orbital path (the condition that prevented Pluto from remaining a planet), the issue of size is something to consider. The table below lists the planets, including Pluto, and their approximate diameters in meters.
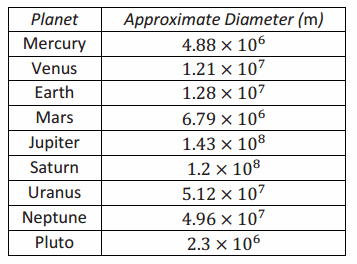
a. Name the planets (including Pluto) in order from smallest to largest.
Answer:
Pluto, mercury, mars, venus, earth, neptune, uranus, saturn, jupiter.
b. Comparing only diameters, about how many times larger is Jupiter than Pluto?
Answer:
\(\frac{1.43 \times 10^{8}}{2.3 \times 10^{6}}\) = \(\frac{1.43}{2.3}\) × \(\frac{10^{8}}{10^{6}}\)
≈ 0.622 × 102
≈ 62.2
The diameter of jupiter is about 62 times larger than pluto.
c. Again, comparing only diameters, find out about how many times larger Jupiter is compared to Mercury.
Answer:
\(\frac{1.43 \times 10^{8}}{4.88 \times 10^{6}}\) = \(\frac{1.43}{4.88}\) × \(\frac{10^{8}}{10^{6}}\)
≈ 0.293 × 102
≈ 29.3
The diameter of jupiter is about 29 times larger than mercury.
d. Assume you are a voting member of the International Astronomical Union (IAU) and the classification of Pluto is based entirely on the length of the diameter. Would you vote to keep Pluto a planet or reclassify it? Why or why not?
Answer:
I would vote to reclassify it. Knowing that jupiter is 29 times larger than mercury means mercury is pretty small. Jupiter is 42 times larger than pluto, which means pluto is even. Smaller than mercury. For that reason vote that the length of the diameter of pluto is too small compared to other planets (Even the small one).
e. Just for fun, Scott wondered how big a planet would be if its diameter was the square of Pluto’s diameter. If the diameter of Pluto in terms of meters were squared, what would the diameter of the new planet be? (Write answer in scientific notation.) Do you think it would meet any size requirement to remain a planet? Would it be larger or smaller than Jupiter?
Answer:
(2.3 × 106)2 = 2.32 × (106)2
= 5.29 × 1012
Yes, 5.29 × 1012 would likely meet any size requirement for planets. It would be larger than jupiter.
Question 3.
Your friend Pat bought a fish tank that has a volume of 175 liters. The brochure for Pat’s tank lists a “fun fact” that it would take 7.43×1018 tanks of that size to fill all the oceans in the world. Pat thinks the both of you can quickly calculate the volume of all the oceans in the world using the fun fact and the size of her tank.
a. Given that 1 liter =1.0×10-12 cubic kilometers, rewrite the size of the tank in cubic kilometers using scientific notation.
Answer:
175 litres = 175(1.0×10-12) cubic kilometers
= 175 ×10-12 km3
= 1.75 × 10-10 km3
b. Determine the volume of all the oceans in the world in cubic kilometers using the “fun fact.”
Answer:
(1.75 × 10-10)(7.43×1018) = (1.75× 7.43)(10-10×1018)
= 13.0025×108
= 1.30025×109
The volume of all the oceans in the world is (1.30025×109)km3.
c. You liked Pat’s fish so much you bought a fish tank of your own that holds an additional 75 liters. Pat asked you to figure out a different “fun fact” for your fish tank. Pat wants to know how many tanks of this new size would be needed to fill the Atlantic Ocean. The Atlantic Ocean has a volume of 323,600,000 cubic kilometers.
Answer:
Tank: 175+75 = 250 liters
250 liters = 250(1.0×10-12) km3
= 2.50 ×10-12
= 2.5 × 10-10
Atlantic ocean: 323,600,000
= 3.236 × 108 km3
\(\frac{3.236 \times 10^{8}}{2.5 \times 10^{-10}}\) = \(\frac{3.236}{2.5}\) × \(\frac{10^{8}}{10^{-10}}\)
= 1.2944×1018
It would take 1.2944×1018 tanks (of size 250 liters) to fill the atlantic ocean.