Engage NY Eureka Math 7th Grade Module 6 Lesson 8 Answer Key
Eureka Math Grade 7 Module 6 Lesson 8 Exercise Answer Key
Exercises 1–2
1. Use your protractor and ruler to draw right triangle DEF. Label all sides and angle measurements.
a. Predict how many of the right triangles drawn in class are identical to the triangle you have drawn.
b. How many of the right triangles drawn in class are identical to the triangle you drew? Were you correct in your prediction?
Answer:
a. Answers will vary; students may say that they should all be the same since the direction is to draw a right triangle.
b. Drawings will vary; most likely few or none of the triangles in the class are identical. Ask students to reflect on why their prediction was incorrect if it was in fact incorrect.
2.
Given the following three sides of △ABC, use your compass to copy the triangle. The longest side has been copied for you already. Label the new triangle A’B’C’, and indicate all side and angle measurements. For a reminder of how to begin, refer to Lesson 6 Exploratory Challenge Problem 10.
A ________________ B
B _____________________C
A ___________________________ C
Answer:
Students must learn how to determine the third vertex of a triangle, given three side lengths. This skill is anchored in the understanding that a circle drawn with a radius of a given segment shows every possible location of one endpoint of that segment (with the center being the other endpoint).
Depending on how challenging students find the task, the following instructions can be provided as a scaffold to the problem. Note that student drawings use prime notation, whereas the original segments do not.
i) Draw a circle with center A’ and radius AB.
ii) Draw a circle with center C’ and radius BC.
iii) Label the point of intersection of the two circles above A’C’ as B’ (the intersection below A’C’ works as well).
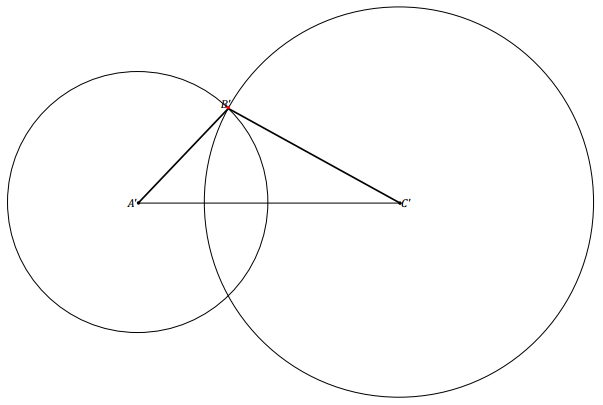
→ How many of the triangles drawn in class are identical?
→ All the drawings should be identical. With three provided side lengths, there is only one way to draw the triangle.
Eureka Math Grade 7 Module 6 Lesson 8 Exploratory Challenge Answer Key
A triangle is to be drawn provided the following conditions: the measurements of two angles are 30° and 60°, and the length of a side is 10 cm. Note that where each of these measurements is positioned is not fixed.
a. How is the premise of this problem different from Exercise 2?
b. Given these measurements, do you think it will be possible to draw more than one triangle so that the triangles drawn will be different from each other? Or do you think attempting to draw more than one triangle with these measurements will keep producing the same triangle, just turned around or flipped about?
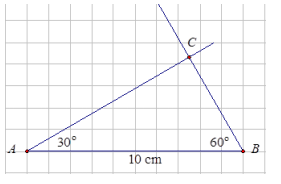
c. Based on the provided measurements, draw △ABC so that ∠A = 30°, ∠B = 60°, and AB = 10 cm. Describe how the 10 cm side is positioned.
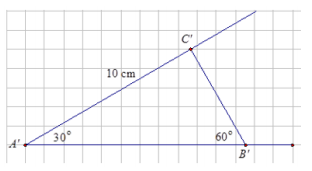
d. Now, using the same measurements, draw △A’B’C’ so that ∠A’ = 30°, ∠B’ = 60°, and AC = 10 cm. Describe how the 10 cm side is positioned.
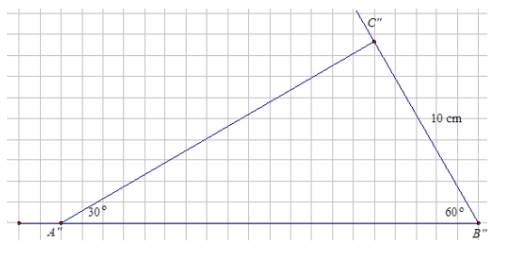
e. Lastly, again, using the same measurements, draw △A”B”C” so that ∠A” = 30°, ∠B” = 60°, and B” C” = 10 cm. Describe how the 10 cm side is positioned.
f. Are the three drawn triangles identical? Justify your response using measurements.
g. Draw △A”’B”’C”’ so that ∠B”’ = 30°, ∠C”’ = 60°, and B^”’ C^”’ = 10 cm. Is it identical to any of the three triangles already drawn?
h. Draw another triangle that meets the criteria of this challenge. Is it possible to draw any other triangles that would be different from the three drawn above?
Answer:
a. In that exercise, we drew a triangle with three provided lengths, while in this problem we are provided two angle measurements and one side length; therefore, the process of drawing this triangle will not require a compass at all.
b. Responses will vary. Possible response: I think more than one triangle can be drawn because we only know the length of one side, and the lengths of the two remaining sides are still unknown. Since two side lengths are unknown, it is possible to have different side lengths and build several different triangles.
c. The 10 cm side is between ∠A and ∠B.
d. Now, using the same measurements, draw △A’B’C’ so that ∠A’ = 30°, ∠B’ = 60°, and AC = 10 cm. Described how the 10 cm side is positioned.
The 10 cm side is opposite to ∠B.
e. Lastly, again, using the same measurements, draw △A”B”C” so that ∠A” = 30°, ∠B” = 60°, and B^” C^” = 10 cm. Describe how the 10 cm side is positioned.
The 10 cm side is opposite to ∠A.
f. No. If the triangles were identical, then the 30° and 60° angles would match, and the other angles, ∠C, ∠C’, and ∠C” would have to match, too. The side opposite ∠C is 10 cm. The side opposite ∠C’ is between 11 and 12 cm. The side opposite ∠C” is 20 cm. There is no correspondence to match up all the angles and all the sides; therefore, the triangles are not identical.
g. It is identical to the triangle in part (d).
h. No, it will be identical to one of the triangles above. Even though the same letters may not line up, the triangle can be rotated or flipped so that there will be some correspondence that matches up equal sides and equal angles.
Eureka Math Grade 7 Module 6 Lesson 8 Problem Set Answer Key
Question 1.
Draw three different acute triangles XYZ, X’Y’Z’, and X”Y”Z” so that one angle in each triangle is 45°. Label all sides and angle measurements. Why are your triangles not identical?
Answer:
Drawings will vary; the angle measurements are not equal from triangle to triangle, so there is no correspondence that will match equal angles to equal angles.
Question 2.
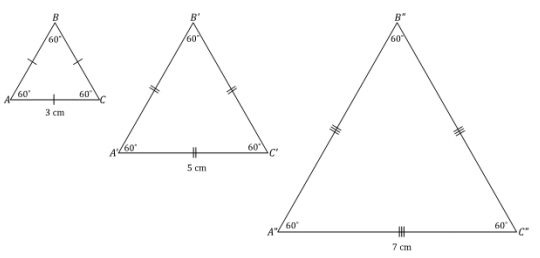
Draw three different equilateral triangles ABC, A’B’C’, and A”B”C”. A side length of △ABC is 3 cm. A side length of △A’B’C’ is 5 cm. A side length of △A”B”C” is 7 cm. Label all sides and angle measurements. Why are your triangles not identical?
Answer:
The location of vertices may vary; all angle measurements are 60°. Though there is a correspondence that will match equal angles to equal angles, there is no correspondence that will match equal sides to equal sides.
Question 3.
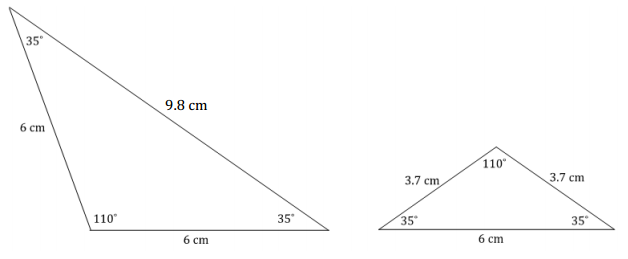
Draw as many isosceles triangles that satisfy the following conditions: one angle measures 110°, and one side measures 6 cm. Label all angle and side measurements. How many triangles can be drawn under these conditions?
Answer:
Two triangles
Question 4.
Draw three nonidentical triangles so that two angles measure 50° and 60° and one side measures 5 cm.
a. Why are the triangles not identical?
b. Based on the diagrams you drew for part (a) and for Problem 2, what can you generalize about the criterion of three given angles in a triangle? Does this criterion determine a unique triangle?
Answer:
a. Though there is a correspondence that will match equal angles to equal angles, there is no correspondence that will match equal sides to equal sides.
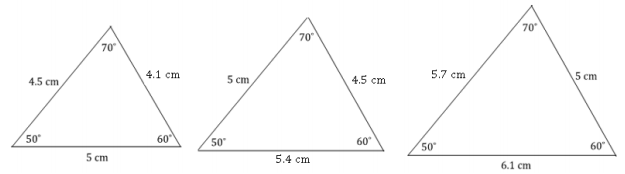
b. No, it is possible to draw nonidentical triangles that all have the same three angle measurements but have different corresponding side lengths.
Eureka Math Grade 7 Module 6 Lesson 8 Exit Ticket Answer Key
Question 1.
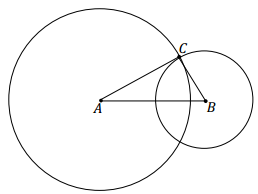
A student is given the following three side lengths of a triangle to use to draw a triangle.
______
__________
_______________
The student uses the longest of the three segments as side \(\overline{A B}\) of triangle △ABC. Explain what the student is doing with the two shorter lengths in the work below. Then, complete the drawing of the triangle.

Answer:
The student drew a circle with center A and a radius equal in length to the medium segment and a circle with center B and a radius equal in length to the smallest segment. The points of the circle A are all a distance equal to the medium segment from point A, and the points of the circle B are all a distance equal to the smallest segment from point B. The point where the two circles intersect indicates where both segments would meet when drawn from A and B, respectively.
Question 2.
Explain why the three triangles constructed in parts (c), (d), and (e) of the Exploratory Challenge were nonidentical.
Answer:
They were nonidentical because the two angles and one side length could be arranged in different ways that affected the structure of the triangle. The different arrangements resulted in differences in angle measurements and side lengths in the remaining parts.