Engage NY Eureka Math 7th Grade Module 6 Lesson 4 Answer Key
Eureka Math Grade 7 Module 6 Lesson 4 Example Answer Key
Example 1.
Find the measurements of ∠FAE and ∠CAD.

Answer:
2x + 6x + 90 = 170 Vert. ∠s
8x + 90 = 170
8x + 90 – 90 = 170 – 90
8x = 80
(\(\frac{1}{8}\))8x = (\(\frac{1}{8}\))80
x = 10
The measurement of ∠FAE: 2(10)° = 20°
The measurement of ∠CAD: 6(10)° = 60°
Two lines meet at a point. List the relevant angle relationship in the diagram. Set up and solve an equation to find the value of x. Find the measurement of one of the vertical angles.
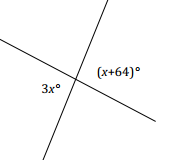
Students use information in the figure and a protractor to solve for x.
i) Students measure a 64° angle as shown; the remaining portion of the angle must be x° (∠s add).
ii) Students can use their protractors to find the measurement of x° and use this measurement to partition the other angle in the vertical pair.
As a check, students should substitute the measured x value into each expression and evaluate; each angle of the vertical pair should be equal to the other. Students can also use their protractor to measure each angle of the vertical angle pair.
With a modified figure, students can write an algebraic equation that they have the skills to solve.
v
2x = 64 Vert.∠s
(\(\frac{1}{2}\))2x = (\(\frac{1}{2}\))64
x = 32
Extension:
3x = x + 64 vert.∠s
3x – x = x – x + 64
2x = 64
(\(\frac{1}{2}\))2x = (\(\frac{1}{2}\))64
x = 32
Measurement of each angle in the vertical pair: 3(32)° = 96°
Example 2.
Three lines meet at a point. List the relevant angle relationships in the diagram. Set up and solve an equation to find the value of b.
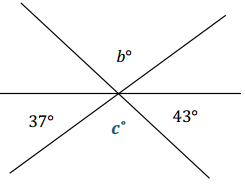
Answer:
Let b = c.
c + 37 + 43 = 180 ∠s on a line
c + 80 = 180
c + 80 – 80 = 180 – 80
c = 100
Since b = c, b = 100.
Example 3.
The measurement of an angle is \(\frac{2}{3}\) the measurement of its supplement. Find the measurements of the angle and its supplement.
Answer:
angle = \(\frac{2}{3}\)(supplement)
angle = \(\frac{2}{3}\)(180 – angle)
Using a tape diagram:

The measurements of the two supplementary angles that satisfy these criteria are 72° and 108°.
The tape diagram model is an ideal strategy for this question. If students are not familiar with the tape diagram model, use a Guess and Check table with them. Here is an example of such a table with two entries for guesses that did not result in a correct answer.

Example 4.
Three lines meet at a point that is also the endpoint of a ray. List the relevant angle relationships in the diagram. Set up and solve an equation to find the value of z.
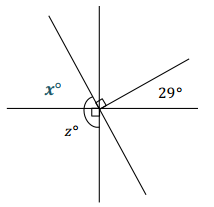
Answer:
Let x° be the measurement of the indicated angle.
x + 90 + 29 = 180 ∠s on a line
x + 119 = 180
x + 119 – 119 = 180 – 119
x = 61
z = x + 90 ∠s add
z = 61 + 90
z = 151
Eureka Math Grade 7 Module 6 Lesson 4 Exercise Answer Key
Exercise 1.
Set up and solve an equation to find the value of x. List the relevant angle relationship in the diagram. Find the measurement of one of the vertical angles.
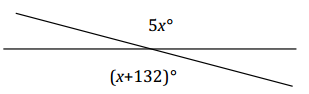
Answer:
Students use information in the figure and a protractor to solve for x.
i) Measure a 132° angle as shown; the remaining portion of the original angle must be x° (∠s add).
ii) Partition the other angle in the vertical pair into equal angles of x°.
Students should perform a check (as in Example 1) before solving an equation that matches the modified figure.

Extension:
4x = 132 vert.∠s
(\(\frac{1}{4}\))4x = (\(\frac{1}{4}\))132
x = 33
Measurement of each vertical angle: 5(33)° = 165°
Note: Students can check their answers for any question by measuring each unknown angle with a protractor, as all diagrams are drawn to scale.
Exercise 2.
Two lines meet at a point that is also the endpoint of two rays. List the relevant angle relationships in the diagram. Set up and solve an equation to find the value of b.
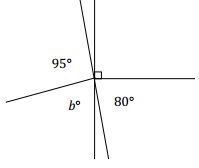
Answer:
b + 95 = 90 + 80 Vert. ∠s
b + 95 = 170
b + 95 – 95 = 170 – 95
b = 75
Exercise 3.
The measurement of an angle is \(\frac{1}{4}\) the measurement of its complement. Find the measurements of the two complementary angles.
Answer:
angle = \(\frac{1}{4}\)(complement)
angle = \(\frac{1}{4}\)(90 – angle)
Using a tape diagram:

5 units = 90
1 unit = 18
4 units = 72
The measurements of the two complementary angles that satisfy these criteria are 18° and 72°.
Exercise 4.
Two lines meet at a point that is also the vertex of an angle. Set up and solve an equation to find the value of x. Find the measurements of ∠GAF and ∠BAC.
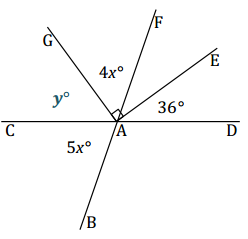
Answer:
Let y° be the measurement of the indicated angle.
y = 180 – (90 + 36) ∠s on a line
y = 54
4x + y + 5x = 180 ∠s on a line
4x + 54 + 5x = 180
9x + 54 = 180
9x + 54 – 54 = 180 – 54
9x = 126
(\(\frac{1}{9}\))9x = (\(\frac{1}{9}\))126
x = 14
The measurement of ∠GAF: 4(14)° = 56°
The measurement of ∠BAC: 5(14)° = 70°
Eureka Math Grade 7 Module 6 Lesson 4 Problem Set Answer Key
Question 1.
Four rays have a common endpoint on a line. Set up and solve an equation to find the value of c.

Answer:
59 + d = 90 Complementary ∠s
59 – 59 + d = 90 – 59
d = 31
d + c + 140 = 180 ∠s on a line
31 + c + 140 = 180
c + 171 = 180
c + 171 – 171 = 180 – 171
c = 9
Question 2.
Lines BC and EF meet at A. Set up and solve an equation to find the value of x. Find the measurements of ∠EAH and ∠HAC.

Answer:
∠BAE + 57 = 90 Complementary ∠s
∠BAE + 57 – 57 = 90 – 57
∠BAE = 33
∠BAE + 3x + 4x = 180 ∠s on a line
33 + 3x + 4x = 180
33 + 7x = 180
33 – 33 + 7x = 180 – 33
7x = 147
(\(\frac{1}{7}\))7x = (\(\frac{1}{7}\))147
x = 21
The measurement of ∠EAH: 3(21)° = 63°
The measurement of ∠HAC: 4(21)° = 84°
Question 3.
Five rays share a common endpoint. Set up and solve an equation to find the value of x. Find the measurements of ∠DAG and ∠GAH.
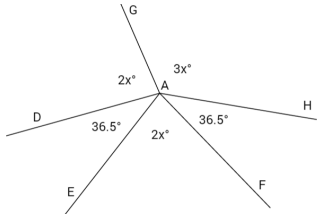
Answer:
2x + 36.5 + 36.5 + 2x + 3x = 360 ∠s at a point
7x + 73 = 360
7x + 73 – 73 = 360 – 73
7x = 287
(\(\frac{1}{7}\))7x = (\(\frac{1}{7}\))287
x = 41
The measurement of ∠EAF: 2(41)° = 82°
The measurement of ∠GAH: 3(41)° = 123°
Question 4.
Four lines meet at a point which is also the endpoint of three rays. Set up and solve an equation to find the values of x and y.

Answer:
2y + 12 + 15 + 90 = 180 ∠s on a line
2y + 117 = 180
2y + 117 – 117 = 180 – 117
2y = 63
(\(\frac{1}{2}\))2y = (\(\frac{1}{2}\))63
y = 31.5
3x = 2y Vert. ∠s
3x = 2(31.5)
3x = 63
(\(\frac{1}{3}\))3x = (\(\frac{1}{3}\))63
x = 21
Question 5.
Two lines meet at a point that is also the vertex of a right angle. Set up and solve an equation to find the value of x. Find the measurements of ∠CAE and ∠BAG.
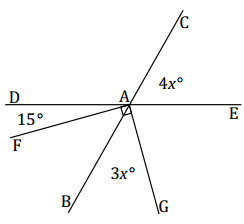
Answer:
∠DAB = 4x vert. ∠s
∠DAG = 90 + 15 = 105 ∠s add
4x + 3x = 105
7x = 105 ∠s add
(\(\frac{1}{7}\))7x = (\(\frac{1}{7}\))105
x = 15
The measurement of ∠CAE: 4(15)° = 60°
The measurement of ∠BAG: 3(15)° = 45°
Question 6.
6. Five angles are at a point. The measurement of each angle is one of five consecutive, positive whole numbers.
a. Determine the measurements of all five angles.
b. Compare the expressions you used for the five angles and their combined expression. Explain how they are equivalent and how they reveal different information about this situation.
Answer:
x + (x + 1) + (x + 2) + (x + 3) + (x + 4) = 360
5x + 10 = 360
5x + 10 – 10 = 360 – 10
5x = 350
(\(\frac{1}{5}\))5x = (\(\frac{1}{5}\))350
x = 70
Angle measures are 70°, 71°, 72°, 73°, and 74°.
b. By the commutative and associative laws, x + (x + 1) + (x + 2) + (x + 3) + (x + 4) is equal to (x + x + x + x + x) + (1 + 2 + 3 + 4), which is equal to 5x + 10. The first expression, x + (x + 1) + (x + 2) + (x + 3) + (x + 4), shows the sum of five unknown numbers where the second is 1 degree more than the first, the third is 1 degree more than the second, and so on. The expression 5x + 10 shows the sum of five times an unknown number with 10.
Question 7.
Let x° be the measurement of an angle. The ratio of the measurement of the complement of the angle to the measurement of the supplement of the angle is 1:3. The measurement of the complement of the angle and the measurement of the supplement of the angle have a sum of 180°. Use a tape diagram to find the measurement of this angle.
Answer:
(90 – x):(180 – x) = 1:3
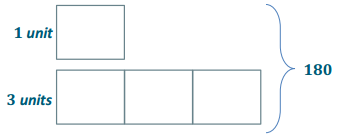
The measurement of the angle that satisfies these criteria is 45°.
Question 8.
Two lines meet at a point. Set up and solve an equation to find the value of x. Find the measurement of one of the vertical angles.

Answer:
A solution can include a modified diagram (as shown) and the supporting algebra work:
3x = 117 vert. ∠s
(\(\frac{1}{3}\))3x = (\(\frac{1}{3}\))117
x = 39
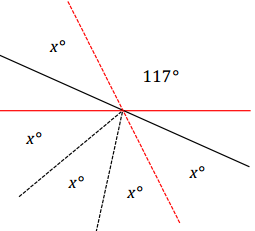
Each vertical angle: 4(39)° = 156°
Solutions may also include the full equation and solution:
4x = x + 117
4x – x = x – x + 117
3x = 117
(\(\frac{1}{3}\))3x = (\(\frac{1}{3}\))117
x = 39
Question 9.
The difference between three times the measurement of the complement of an angle and the measurement of the supplement of that angle is 20°. What is the measurement of the angle?
Answer:
3(90 – x) – (180 – x) = 20
270 – 3x – 180 + x = 20
90 – 2x = 20
90 – 90 – 2x = 20 – 90
– 2x = – 70
( – \(\frac{1}{2}\))( – 2x) = ( – \(\frac{1}{2}\))( – 70)
x = 35
The measurement of the angle is 35°.
Eureka Math Grade 7 Module 6 Lesson 4 Exit Ticket Answer Key
Question 1.
Lines BC and EF meet at A. Rays AG and AD form a right angle. Set up and solve an equation to find the values of x and w.
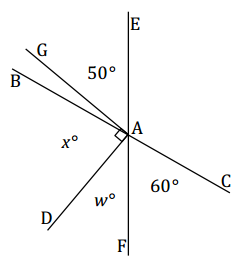
Answer:
∠BAE = 60 Vert. ∠s
∠BAG = 10 ∠s add
x + ∠BAG = 90 Complementary ∠s
x + 10 = 90
x + 10 – 10 = 90 – 10
x = 80
x + w + 60 = 180 ∠s on a line
80 + w + 60 = 180
140 + w = 180
140 + w – 140 = 180 – 140
w = 40