Engage NY Eureka Math 7th Grade Module 6 Lesson 16 Answer Key
Eureka Math Grade 7 Module 6 Lesson 16 Example Answer Key
Example 1.
Consider a ball B. Figure 3 shows one possible slice of B.
a. What figure does the slicing plane form? Students may choose their method of representation of the slice (e.g., drawing a 2D sketch, a 3D sketch, or describing the slice in words).
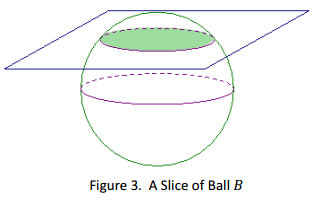
b. Will all slices that pass through B be the same size? Explain your reasoning.
c. How will the plane have to meet the ball so that the plane section consists of just one point?
Answer:
a. A circle (or disc)
b. No, different slices can result in circles of different sizes; it will depend on where the slicing plane meets the ball.
c. If you picture the ball and the plane as distinct but being brought toward each other, the plane section of just one point occurs when the plane just makes contact with the ball.
Example 2.
The right rectangular prism in Figure 4 has been sliced with a plane parallel to face ABCD. The resulting slice is a rectangular region that is identical to the parallel face.
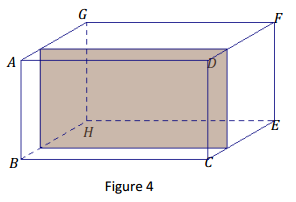
a. Label the vertices of the rectangular region defined by the slice as WXYZ.
b. To which other face is the slice parallel and identical?
c. Based on what you know about right rectangular prisms, which faces must the slice be perpendicular to?
Answer:
a. 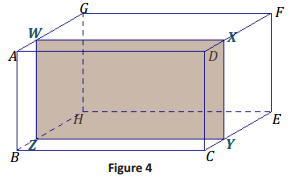
b. The slice is parallel and identical to the face EFGH.
c. Since the slice is parallel to two faces, it will be perpendicular to whichever sides those faces are perpendicular to. Therefore, the slice is perpendicular to faces ABHG, CDFE, BCEH, and ADFG.
Example 3.
The right rectangular prism in Figure 6 has been sliced with a plane perpendicular to BCEH. The resulting slice is a rectangular region with a height equal to the height of the prism.
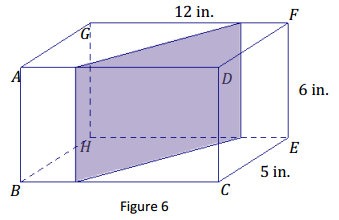
a. Label the vertices of the rectangle defined by the slice as WXYZ.
b. To which other face is the slice perpendicular?
c. What is the height of rectangle WXYZ?
d. Joey looks at WXYZ and thinks that the slice may be a parallelogram that is not a rectangle. Based on what is known about how the slice is made, can he be right? Justify your reasoning.
Answer:
a. 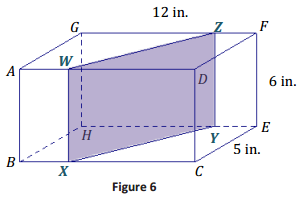
b. The slice is perpendicular to the face ADFG.
c. 6 in.
d. The slice was made perpendicular to face BCEH. Then we know that the angles in the slice, ∠X and ∠Y, formed by the slicing plane and face BCEH, are right angles. If we focus on ∠X of the slice, since it is a right angle, we know that \(\overline{W X}\) must be perpendicular to face BCEH. \(\overline{W X}\) lies in face ABCD, which is perpendicular to both BCEH and to ADFG, so \(\overline{W X}\)is perpendicular to ABCD. This means that \(\overline{W X}\) must also be perpendicular to \(\overline{W Z}\). A similar argument can be made for ∠Y of the slice, making all four angles of WXYZ right angles and making WXYZ a rectangle.
Eureka Math Grade 7 Module 6 Lesson 16 Exercise Answer Key
Exercise 1.
Discuss the following questions with your group.
The right rectangular prism in Figure 5 has been sliced with a plane parallel to face LMON.
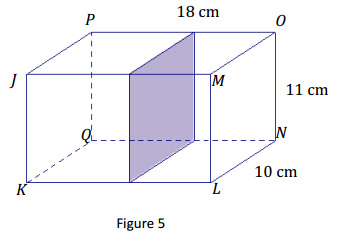
a. Label the vertices of the rectangle defined by the slice as RSTU.
b. What are the dimensions of the slice?
c. Based on what you know about right rectangular prisms, which faces must the slice be perpendicular to?
Answer:
a. 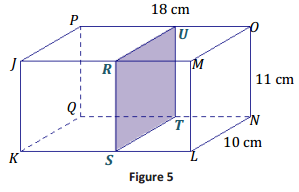
b. 10 cm × 11 cm
c. Since the slice is parallel to two faces, it will be perpendicular to whichever sides those faces are perpendicular to. Therefore, the slice is perpendicular to faces JKLM, JMOP, NOPQ, and KLNQ.
In the following exercises, the points at which a slicing plane meets the edges of the right rectangular prism have been marked. Each slice is either parallel or perpendicular to a face of the prism. Use a straightedge to join the points to outline the rectangular region defined by the slice, and shade in the rectangular slice.
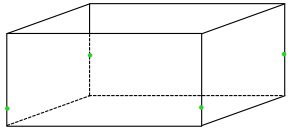
Exercise 2.
A slice parallel to a face
Answer:
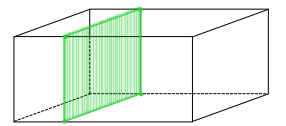
Exercise 3.
A slice perpendicular to a face
Answer:
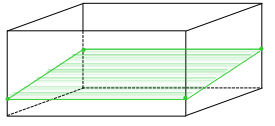
Exercise 4.
A slice perpendicular to a face
Answer:
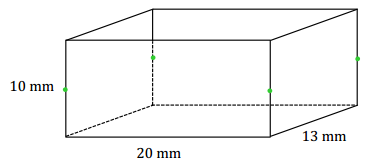
In Exercises 5–6, the dimensions of the prisms have been provided. Use the dimensions to sketch the slice from each prism, and provide the dimensions of each slice.
Exercise 5.
A slice parallel to a face
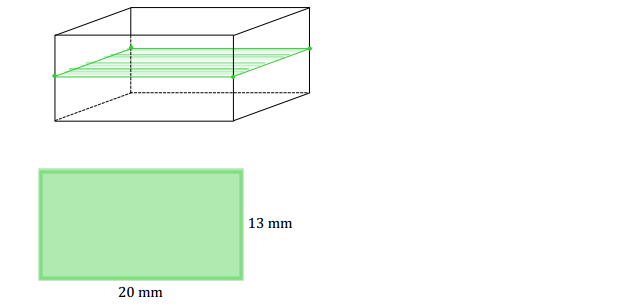
Answer:
Exercise 6.
A slice perpendicular to a face
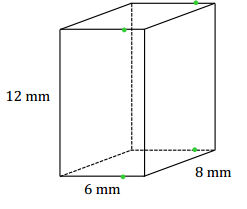
Answer:
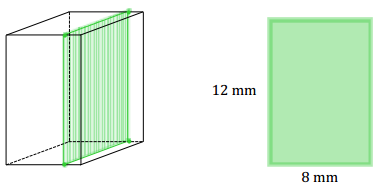
Eureka Math Grade 7 Module 6 Lesson 16 Problem Set Answer Key
Question 1.
A right rectangular prism is shown along with line segments that lie in a face. For each line segment, draw and give the approximate dimensions of the slice that results when the slicing plane contains the given line segment and is perpendicular to the face that contains the line segment.
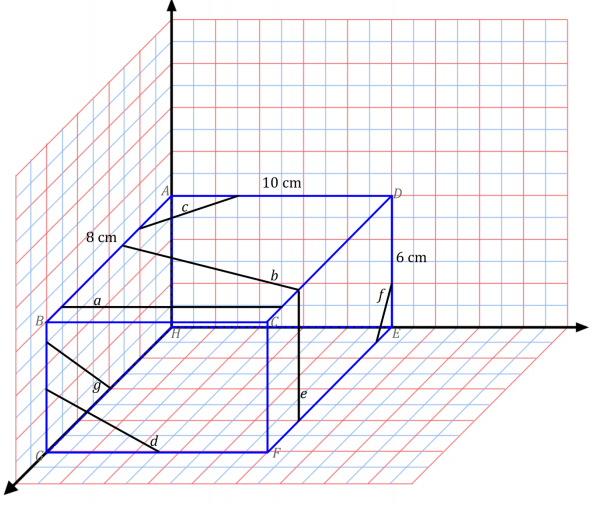
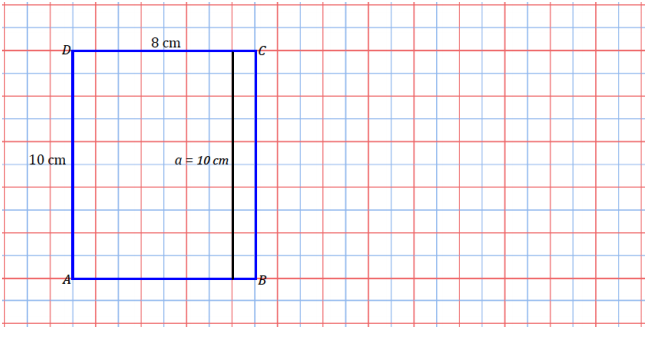
a.
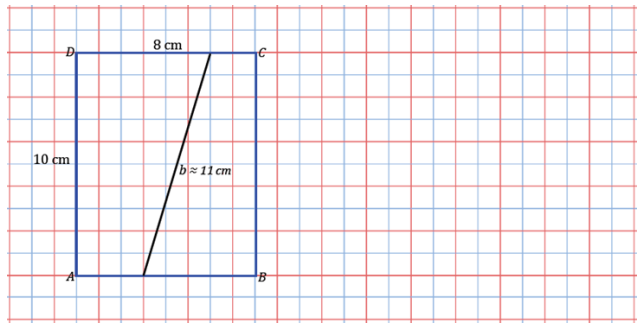
b.
c.
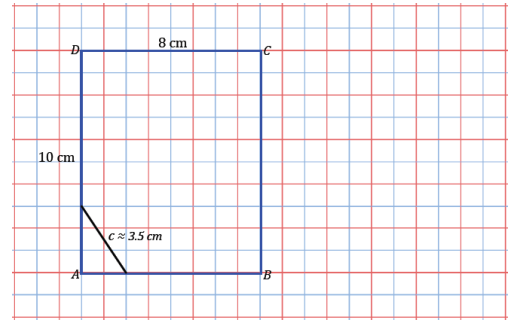
d.
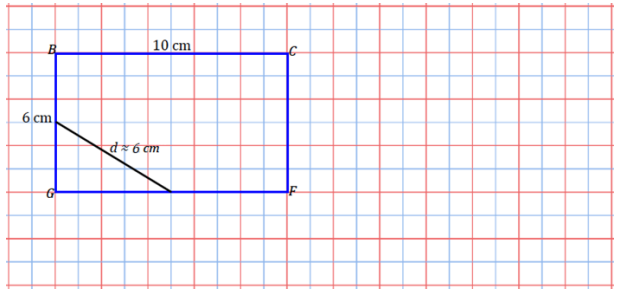
e.
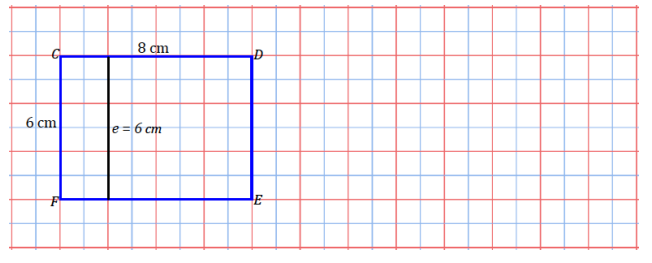
f.
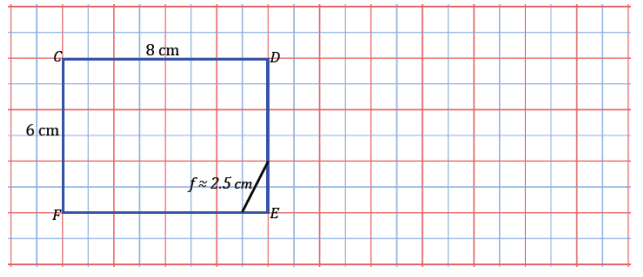
g.
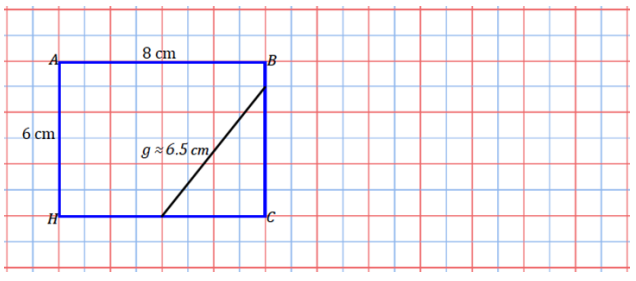
Answer:
a.
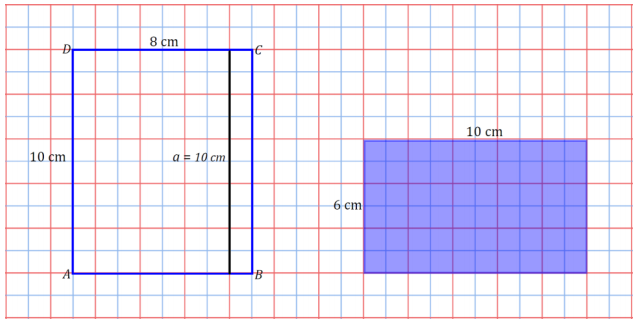
b.
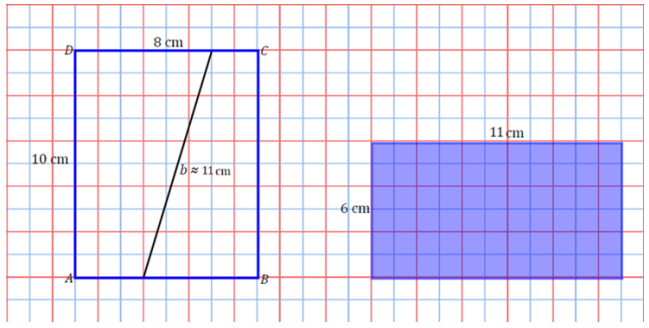
c.
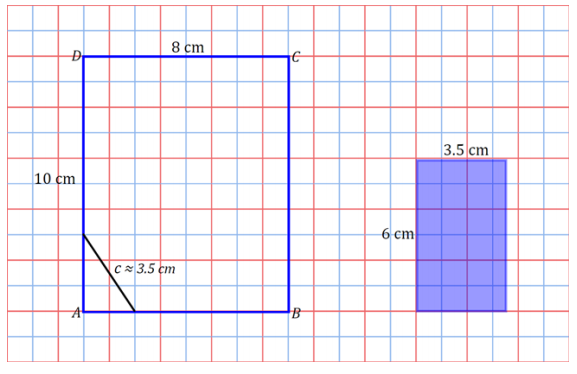
d.
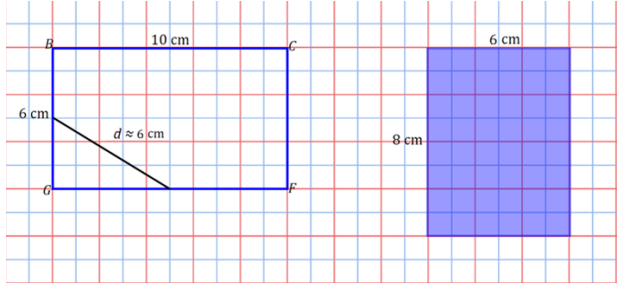
e.
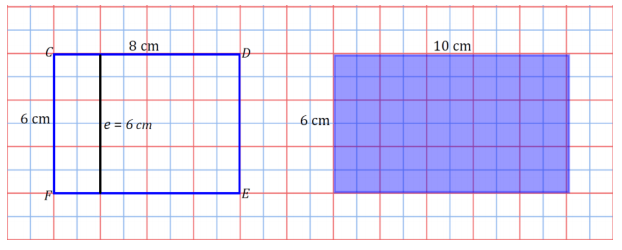
f.
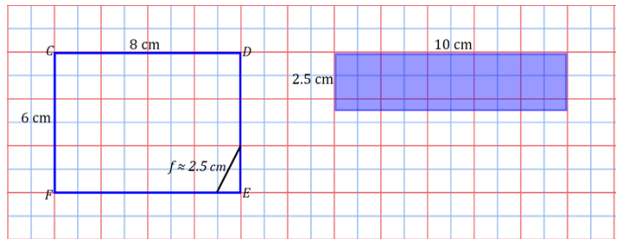
g.
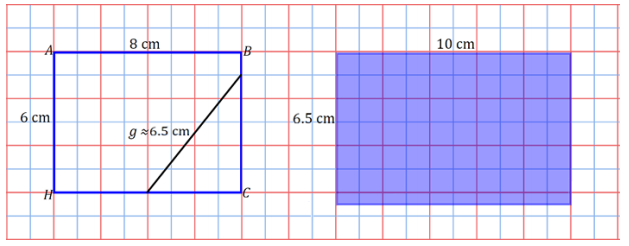
Eureka Math Grade 7 Module 6 Lesson 16 Exit Ticket Answer Key
In the following figures, use a straightedge to join the points where a slicing plane meets with a right rectangular prism to outline the slice.
i) Label the vertices of the rectangular slice WXYZ.
ii) State any known dimensions of the slice.
iii) Describe two relationships slice WXYZ has in relation to faces of the right rectangular prism.
Question 1.
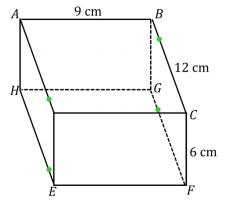
Answer:
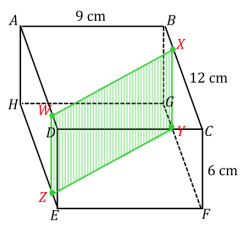
Sides \(\overline{W Z}\) and \(\overline{X Y}\) are 6 cm in length. Slice WXYZ is perpendicular to faces ABCD and EFGH.
Question 2.
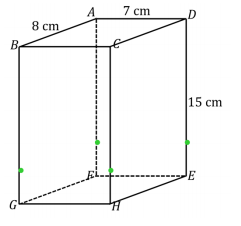
Answer:
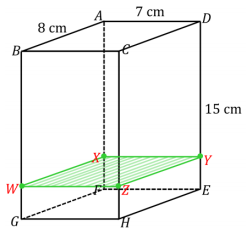
Sides \(\overline{W Z}\) and \(\overline{X Y}\) are 7 cm in length. Sides \(\overline{W X}\) and \(\overline{Z Y}\) are 8 cm in length. Slice WXYZ is parallel to faces ABCD and EFGH and perpendicular to faces CDEH, ADEF, ABGF, and BCHG.
Note: Students are only required to state two of the relationships the slice has with the faces of the prism.