Engage NY Eureka Math 7th Grade Module 6 Lesson 14 Answer Key
Eureka Math Grade 7 Module 6 Lesson 14 Example Answer Key
Example 1.
What is the relationship between the two triangles below?
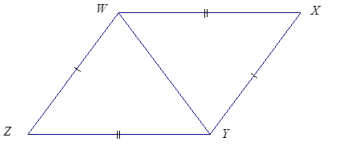
Answer:
What is the relationship between the two triangles below?
The triangles share a common side.
Imagine that △WXY and △WZY were pulled apart and separated. Sketch the triangles separately. Based on how they were joined, what kind of tick mark should be added to each triangle?
\(\overline{W Y}\) is a common side. Since it belongs to each triangle, we should put a triple tick mark on \(\overline{W Y}\) to indicate that it is a part of equal measure in both triangles.
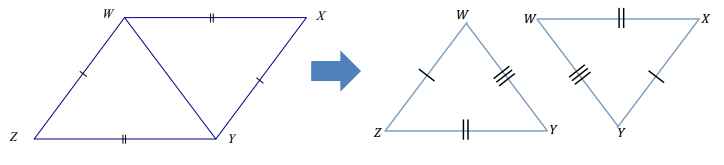
Are the triangles identical? How do you know?
The triangles are identical by the three sides condition. The correspondence that matches the three equal pairs of sides is △WXY↔△YZW.
Example 2.
Are the triangles identical? Justify your reasoning.
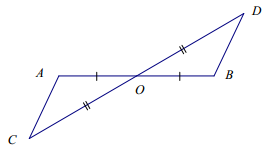
Answer:
The triangles are identical by the two sides and the included angle condition. The correspondence △AOC ↔ △BOD matches two equal pairs of sides and a pair of equal angles, ∠AOC = ∠BOD, which we know to be equal in measurement because they are vertical angles.
Eureka Math Grade 7 Module 6 Lesson 14 Exercise Answer Key
Exercise 1.
Are the triangles identical? Justify your reasoning.
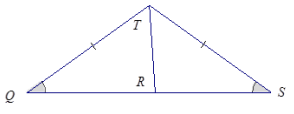
Answer:
The triangles are not necessarily identical. The correspondence △QRT ↔ △SRT matches a pair of equal angles and a pair of equal sides. The correspondence also matches a common side, \(\overline{R T}\), to both triangles. Two sides and a non-included acute angle do not necessarily determine a unique triangle.
Exercise 2.
Are the triangles identical? Justify your reasoning.
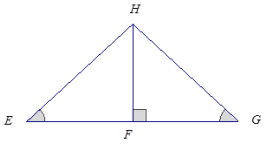
Answer:
These triangles are identical by the two angles and side opposite a given angle condition. The correspondence △EFH ↔ △GFH matches two pairs of equal angles and a pair of equal sides. ∠HFE must be a right angle since ∠HFG is a right angle, and they are both on a line. Also, \(\overline{H F}\) is a common side to both triangles. Since both triangles have parts under the condition of the same measurement, the triangles must be identical.
Exercise 3.
Are the triangles identical? Justify your reasoning.
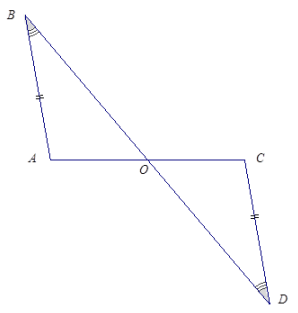
Answer:
These triangles are identical by the two angles and side opposite a given angle condition. The correspondence △AOB ↔ △COD matches the two pairs of equal angles and one pair of equal sides. There is a marked pair of equal sides and one pair of marked, equal angles. The second pair of equal angles, ∠AOB = ∠COD, are vertical angles.
Exercise 4.
Are the triangles identical? Justify your reasoning.
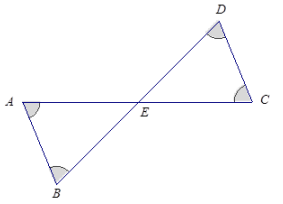
Answer:
The triangles are not necessarily identical. The correspondence △AEB ↔ △CED matches three pairs of equal angles, including the unmarked angles, ∠AEB and ∠CED, which are equal in measurement because they are vertical angles. The triangles could have different side lengths; therefore, they are not necessarily identical.
Exercise 5.
Are the triangles identical? Justify your reasoning.
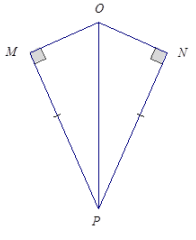
Answer:
The triangles are identical by the two sides and non-included 90° (or greater) angle condition. The correspondence △MPO ↔ △NPO matches two pairs of equal sides and one pair of equal angles. One of the two pairs of equal sides is side \(\overline{O P}\), which is common to both triangles.
Exercise 6.
Are the triangles identical? Justify your reasoning.
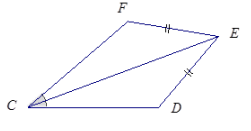
Answer:
These triangles are not necessarily identical. The triangles have a pair of marked equal sides and equal angles; side \(\overline{C E}\) is also common to both triangles. The triangles satisfy the two sides and non-included acute angle condition, which does not determine a unique triangle.
Exercise 7.
Are the triangles identical? Justify your reasoning.
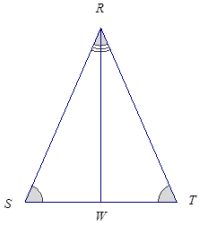
Answer:
These triangles are identical by the two angles and a side opposite a given angle condition. The triangle correspondence △RWS ↔ △RWT matches two pairs of equal angles and one pair of equal sides. The equal pair of sides, \(\overline{R W}\), is common to both triangles.
Exercise 8.
Create your own labeled diagram and set of criteria for a pair of triangles. Ask a neighbor to determine whether the triangles are identical based on the provided information.
Answer:
Answers will vary.
Eureka Math Grade 7 Module 6 Lesson 14 Problem Set Answer Key
In the following problems, determine whether the triangles are identical, not identical, or not necessarily identical; justify your reasoning. If the relationship between the two triangles yields information that establishes a condition, describe the information. If the triangles are identical, write a triangle correspondence that matches the sides and angles.
Question 1.
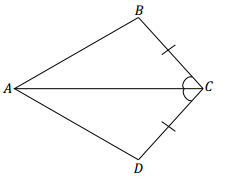
Answer:
These triangles are identical by the two sides and the included angle condition. The triangle correspondence △ABC ↔ △ADC matches two pairs of equal sides and one pair of equal angles. One of the equal pairs of sides is shared side \(\overline{A C}\).
Question 2.
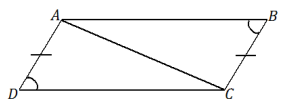
Answer:
These triangles are not necessarily identical. The triangles have a pair of marked equal sides, and a pair of marked, acute, equal angles; side \(\overline{A C}\) is also common to both triangles. The triangles satisfy the two sides and non-included acute angle condition, which does not determine a unique triangle.
Question 3.
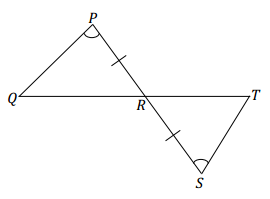
Answer:
These triangles are identical by the two angles and included side condition. The triangle correspondence △QPR ↔ △TSR matches the two pairs of equal angles and one pair of equal sides. One pair of equal angles is the vertical angle pair ∠PRQ = ∠SRT.
Question 4.

Answer:
These triangles are not necessarily identical. A correspondence that matches up the equal pair of sides and the equal pair of vertical angles does not match the marked equal pair of angles.
Question 5.
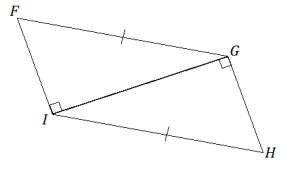
Answer:
The triangles are identical by the two sides and non-included 90° (or greater) angle condition. The correspondence △IFG ↔ △GHI matches two pairs of equal sides and one pair of equal angles. One of the two pairs of equal sides is side \(\overline{I G}\), which is common to both triangles.
Question 6.
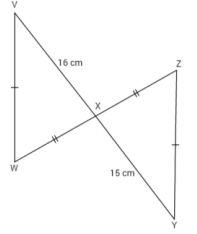
Answer:
The triangles are not identical since a correspondence that matches the two marked equal pairs of sides also matches sides \(\overline{V X}\) and \(\overline{X Y}\), which are not equal in length.
Question 7.
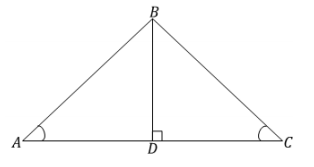
Answer:
These triangles are identical by the two angles and side opposite a given angle condition. The correspondence △ABD ↔ △CBD matches the two pairs of equal angles and one pair of equal sides. The pair of equal sides is the common side, \(\overline{B D}\). We know ∠ADB must be a right angle since ∠CDB is a right angle; they are both on a line, and of course angles ∠A and ∠C are equal in measurement.
Question 8.
Are there any identical triangles in this diagram?

Answer:
△TUX and △VWX are not necessarily identical; we only know about a single pair of equal angles in the triangles, which are vertical angles. △TUV and △VWT are also not necessarily identical. We only know about a single pair of equal angles and a side common to both triangles, which is not enough information to determine the triangles as identical or non-identical.
Question 9.
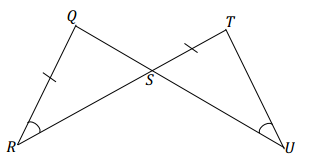
Answer:
The triangles are not necessarily identical since there is no correspondence that matches the two marked equal pairs of sides as well as the two pairs of equal angles. One of the pairs of equal angles is the pair of vertical angles.
Question 10.
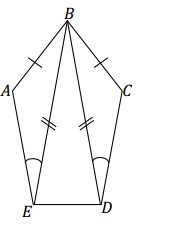
Answer:
△ABE and △CBD are not necessarily identical. The triangles satisfy the two sides and non-included acute angle condition, which does not determine a unique triangle.
Eureka Math Grade 7 Module 6 Lesson 14 Exit Ticket Answer Key
Question 1.
Are △DEF and △DGF identical, not identical, or not necessarily identical? Justify your reasoning. If the relationship between the two triangles yields information that establishes a condition, describe the information. If the triangles are identical, write a triangle correspondence that matches the sides and angles.
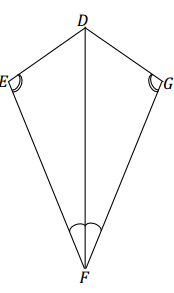
Answer:
These triangles are identical by the two angles and side opposite a given angle condition. The triangle correspondence △DEF ↔ △DGF matches the two pairs of equal angles and one pair of equal sides condition. The pair of equal sides, \(\overline{D F}\), is common to both triangles.