Engage NY Eureka Math 7th Grade Module 3 Mid Module Assessment Answer Key
Eureka Math Grade 7 Module 3 Mid Module Assessment Task Answer Key
Question 1.
Use the expression below to answer parts (a) and (b).
4x-3(x-2y)+\(\frac{1}{2}\)(6x-8y)
a. Write an equivalent expression in standard form, and collect like terms.
Answer:
4x – 3(x – 2y) + \(\frac{1}{2}\)(6x – 8y)
4x – 3x + 6y + 3x – 4y
4x – 3x + 3x + 6y – 4y
4x + 2y
b. Express the answer from part (a) as an equivalent expression in factored form.
Answer:
4x + 2y
2(2x + y)
Question 2.
Use the information to solve the problems below.
a. The longest side of a triangle is six more units than the shortest side. The third side is twice the length of the shortest side. If the perimeter of the triangle is 25 units, write and solve an equation to find the lengths of all three sides of the triangle.
Answer:
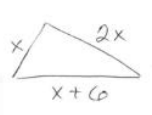
2x + x + x + 6 = 25
4x + 6 = 25
4x + 6 – 6 = 25 – 6
4x + 0 = 19
\(\frac{1}{4}\)(4x) = \(\frac{1}{4}\)(9)
x = \(\frac{19}{4}\)
x = 4\(\frac{3}{4}\)
Smallest side: x = 4\(\frac{3}{4}\)
Largest side: x + 6 = 10\(\frac{3}{4}\)
Third side: 2x = 9\(\frac{1}{2}\)
3 sides are: 4\(\frac{3}{4}\) units, 10\(\frac{3}{4}\) units, 9\(\frac{1}{2}\) units
b. The length of a rectangle is (x+3) inches long, and the width is 3 \(\frac{2}{5}\) inches. If the area is 15 \(\frac{3}{10}\) square inches, write and solve an equation to find the length of the rectangle.
Answer:
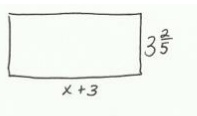
Length: x + 3: = 1\(\frac{1}{2}\) + 3 = 4\(\frac{1}{2}\) inches
Width: 3\(\frac{2}{5}\) inches
3\(\frac{2}{5}\)(x + 3) = 15\(\frac{3}{10}\)
3\(\frac{2}{5}\)x + 3(3\(\frac{2}{5}\)) = 15\(\frac{3}{10}\)
\(\frac{17}{5}\)x + 3(\(\frac{17}{5}\)) = 15\(\frac{3}{10}\)
\(\frac{17}{5}\)x + \(\frac{51}{5}\) = 15\(\frac{3}{10}\)
\(\frac{17}{5}\)x + 10\(\frac{1}{5}\) = 15\(\frac{3}{10}\)
\(\frac{17}{5}\)x + 10\(\frac{1}{5}\) – 10\(\frac{1}{5}\) = 15\(\frac{3}{10}\) – 10\(\frac{1}{5}\)
(\(\frac{17}{5}\)x) + 0 = 5\(\frac{1}{10}\)
\(\frac{5}{17}\)(\(\frac{17}{5}\)x) = (\(\frac{51}{10}\))(\(\frac{5}{17}\))
x = \(\frac{3}{2}\)
x = 1\(\frac{1}{2}\)
Question 3.
A picture 10 \(\frac{1}{4}\) feet long is to be centered on a wall that is 14 \(\frac{1}{2}\) feet long. How much space is there from the edge of the wall to the picture?
a. Solve the problem arithmetically.
Answer:
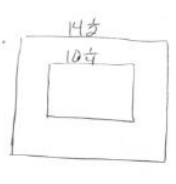
(14\(\frac{1}{2}\) – 10\(\frac{1}{4}\)) ÷ 2
(14\(\frac{2}{4}\) – 10\(\frac{1}{4}\)) ÷ 2
4\(\frac{1}{4}\) ÷ 2
\(\frac{17}{4}\) ÷ 2
\(\frac{17}{4}\) ∙ \(\frac{1}{2}\)
\(\frac{17}{8}\)
2\(\frac{1}{8}\)
The picture is 2\(\frac{1}{8}\) inches from the wall.
b. Solve the problem algebraically.
Answer:
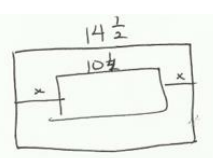
Let x: distance from one side to the picture
x + 10\(\frac{1}{4}\) + x = 14\(\frac{1}{2}\)
2x + 10\(\frac{1}{4}\) = 14\(\frac{1}{2}\)
2x + 10\(\frac{1}{4}\) – 10\(\frac{1}{4}\) = 14\(\frac{1}{2}\) – 10\(\frac{1}{4}\)
2x + 0 = 4\(\frac{1}{4}\)
(\(\frac{1}{2}\)) (2x) = (4\(\frac{1}{4}\))(\(\frac{1}{2}\))
x = (\(\frac{17}{4}\)) (\(\frac{1}{2}\))
x = \(\frac{17}{8}\) = 2\(\frac{1}{8}\)
The picture is 2\(\frac{1}{8}\) inches from the wall.
c. Compare the approaches used in parts (a) and (b). Explain how they are similar.
Answer:
The solutions are the same. The actual operations performed in the equation are the same operations done arithmetically.
Question 4.
In August, Cory begins school shopping for his triplet daughters.
a. One day, he bought 10 pairs of socks for $2.50 each and 3 pairs of shoes for d dollars each. He spent a total of $135.97. Write and solve an equation to find the cost of one pair of shoes.
Answer:
d: cost of shoes
10(2.50) + 3d = 135.97
25 + 3d = 135.97
3d + 25 = 135.97
3d+ 25 – 25 = 135.97 – 25
3d + 0 = 110.97
(\(\frac{1}{3}\))(3d)= (110.97)(\(\frac{1}{3}\))
d = 36.99
The cost of one pair of shoes is 36.99
b. The following day Cory returned to the store to purchase some more socks. He had $40 to spend. When he arrived at the store, the shoes were on sale for \(\frac{1}{3}\) off. What is the greatest amount of pairs of socks Cory can purchase if he purchases another pair of shoes in addition to the socks?
Answer:
Shoes: \(\frac{1}{3}\)(36.99)
12.33 off
New price
36.99 – 12.33 = 24.66
Socks: d
2.50d + 24.66 ≤ 40
2.50d + 24.66 – 24.66 ≤ 40 – 24.66
2.50d + 0 ≤ 15.34
(\(\frac{1}{2.50}\))(2.50d) ≤ (15.34)(\(\frac{1}{2.50}\))
d ≤ 6.136
The greatest amount of socks he can buy is 6 pairs.
Question 5.
Ben wants to have his birthday at the bowling alley with a few of his friends, but he can spend no more than $80. The bowling alley charges a flat fee of $45 for a private party and $5.50 per person for shoe rentals and unlimited bowling.
a. Write an inequality that represents the total cost of Ben’s birthday for p people given his budget.
Answer:
45 + 5.50p ≤ 80
b. How many people can Ben pay for (including himself) while staying within the limitations of his budget?
Answer:
P: number of people invited
45 + 5.50p ≤ 80
5.50p + 45 ≤ 80
5.50p + 45 – 45 ≤ 80 – 45
(\(\frac{1}{5.50}\))(5.50p) ≤ (35)(\(\frac{1}{5.50}\))
P ≤ \(\frac{350}{55}\)
P ≤ \(\frac{70}{11}\)
P ≤ 6\(\frac{4}{11}\)
6 people can attend the party
P ≤ 6
c. Graph the solution of the inequality from part (a).
Answer:

6. Jenny invited Gianna to go watch a movie with her family. The movie theater charges one rate for 3D admission and a different rate for regular admission. Jenny and Gianna decided to watch the newest movie in 3D. Jenny’s mother, father, and grandfather accompanied Jenny’s little brother to the regular admission movie.
a. Write an expression for the total cost of the tickets. Define the variables.
Answer:
d: cost in dollars of 3D admission
r: cost in dollars of regular admission
Jenny Gianna Mother Father Grandfather Brother
d + d + r + r + r + r
2d + 4r
b. The cost of the 3D ticket was double the cost of the regular admission ticket. Write an equation to represent the relationship between the two types of tickets.
Answer:
d = 2r
c. The family purchased refreshments and spent a total of $18.50. If the total amount of money spent on tickets and refreshments was $94.50, use an equation to find the cost of one regular admission ticket.
Answer:
2d + 4r + 18.50 = 94.50
2(2r) + 4r + 18.50 = 94.50
4r + 4r + 18.50 = 94.50
8r + 18.50 = 94.50
8r + 18.50 – 18.50 = 94.50 – 18.50
8r + 0 = 76
(\(\frac{1}{8}\))(8r) = (76)(\(\frac{1}{8}\))
r = 9.5
The cost of one regular admission ticket is $9.50
Question 7.
The three lines shown in the diagram below intersect at the same point. The measures of some of the angles in degrees are given as 3(x – 2)°, \(\frac{3}{5}\) y)°, 12°, 42°.

a. Write and solve an equation that can be used to find the value of x.
Answer:
3(x – 2) = 42
3x – 6 = 42
3x – 6 + 6 = 42 + 6
3x + 0 = 48
(\(\frac{1}{3}\))(3x) = (48)(\(\frac{1}{3}\))
x = 16
OR
\(\frac{1}{3}\)(3(x – 2)) = (42)(\(\frac{1}{3}\))
x – 2 = 14
x – 2 + 2 = 14 + 2
x + 0 = 16
x = 16
b. Write and solve an equation that can be used to find the value of y.
Answer:
\(\frac{3}{5}\) y + 12 + 42 = 180
\(\frac{3}{5}\) y + 54 = 180
\(\frac{3}{5}\) y + 54 – 54 = 180 – 54
\(\frac{3}{5}\) y + 0 = 126
(\(\frac{5}{3}\))(\(\frac{3}{5}\) y) = (126)(\(\frac{5}{3}\))
y = (42)(5)
y = 210