Eureka Math Grade 7 Module 3 Lesson 23 Answer Key

Engage NY Eureka Math 7th Grade Module 3 Lesson 23 Answer Key

Eureka Math Grade 7 Module 3 Lesson 23 Exploratory Challenge Answer Key

Exploratory Challenge: The Volume of a Right Prism
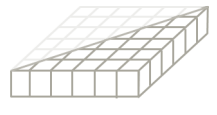
What is the volume of the right prism pictured on the right? Explain.
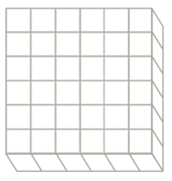
$Engage NY Math 7th Grade Module 3 Lesson 23 Exploratory Challenge Answer Key 1$
Answer:
$Engage NY Math 7th Grade Module 3 Lesson 23 Exploratory Challenge Answer Key 2$
The volume of the right prism is 36 units³ because the prism is filled with 36 cubes that are 1 unit long, 1 unit wide, and 1 unit high, or 1 unit³.

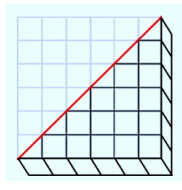
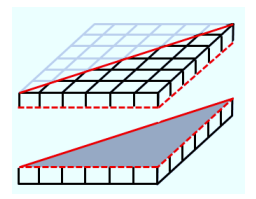
Draw the same diagonal on the square base as done above; then, darken the grid lines on the lower right triangular prism. What is the volume of that right triangular prism? Explain.
Answer:
The volume of the right triangular prism is 18 units³. There are 15 cubes from the original right prism and 6 right triangular prisms that are each half of a cube. The 6 right triangular prisms can be paired together to form 3 cubes, or 3 units³. Altogether the area of the right triangular prism is (15+3) units³, or 18 units³.

How could we create a right triangular prism with five times the volume of the right triangular prism pictured to the right, without changing the base? Draw your solution on the diagram, give the volume of the solid, and explain why your solution has five times the volume of the triangular prism.
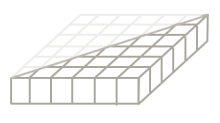
$Engage NY Math 7th Grade Module 3 Lesson 23 Exploratory Challenge Answer Key 3$
Answer:
$Engage NY Math 7th Grade Module 3 Lesson 23 Exploratory Challenge Answer Key 4$
If we stack five exact copies of the base (or bottom floor), the prism then has five times the number of unit cubes as the original, which means it has five times the volume, or 90 units³.

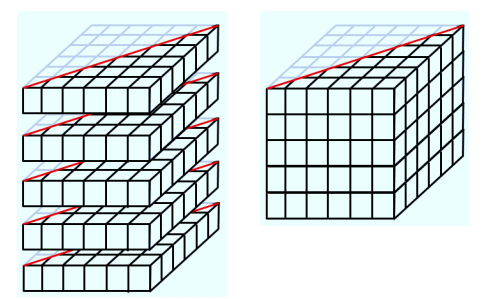
What could we do to cut the volume of the right triangular prism pictured on the right in half without changing the base? Draw your solution on the diagram, give the volume of the solid, and explain why your solution has half the volume of the given triangular prism.
$Engage NY Math 7th Grade Module 3 Lesson 23 Exploratory Challenge Answer Key 5$
Answer:
$Engage NY Math 7th Grade Module 3 Lesson 23 Exploratory Challenge Answer Key 6$
If we slice the height of the prism in half, each of the unit cubes that make up the triangular prism will have half the volume as in the original right triangular prism. The volume of the new right triangular prism is 9 units³.

To find the volume (V) of any right prism …
Answer:
Multiply the area of the right prism’s base (B) times the height of the right prism (h), V = Bh.

Eureka Math Grade 7 Module 3 Lesson 23 Example Answer Key

Example: The Volume of a Right Triangular Prism
Find the volume of the right triangular prism shown in the diagram using V = Bh.
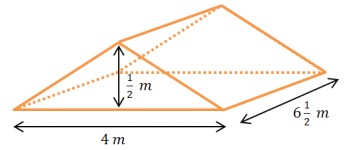
$Engage NY Math 7th Grade Module 3 Lesson 23 Example Answer Key 1$
Answer:
V = Bh
V = ($\frac{1}{2}$ lw)h
V = ($\frac{1}{2}$ ∙ 4 m ∙ $\frac{1}{2}$ m) ∙ 6 $\frac{1}{2}$ m
V = (2 m ∙ $\frac{1}{2}$ m) ∙ 6 $\frac{1}{2}$ m
V = 1 m² ∙ 6 $\frac{1}{2}$ m
V = 6 $\frac{1}{2}$ m³ The volume of the triangular prism is 6 $\frac{1}{2}$ m³.

Eureka Math Grade 7 Module 3 Lesson 23 Exercise Answer Key

Opening Exercise
The volume of a solid is a quantity given by the number of unit cubes needed to fill the solid. Most solids—rocks, baseballs, people—cannot be filled with unit cubes or assembled from cubes. Yet such solids still have volume. Fortunately, we do not need to assemble solids from unit cubes in order to calculate their volume. One of the first interesting examples of a solid that cannot be assembled from cubes, but whose volume can still be calculated from a formula, is a right triangular prism.

What is the area of the square pictured on the right? Explain.
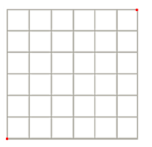
$Engage NY Math Grade 7 Module 3 Lesson 23 Exercise Answer Key 1$
Answer:
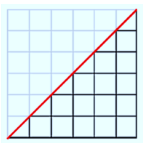
$Engage NY Math Grade 7 Module 3 Lesson 23 Exercise Answer Key 2$
The area of the square is 36 units² because the region is filled with 36 square regions that are 1 unit by 1 unit, or 1 unit².

Draw the diagonal joining the two given points; then, darken the grid lines within the lower triangular region. What is the area of that triangular region? Explain.
Answer:
The area of the triangular region is 18 units². There are 15 unit squares from the original square and 6 triangular regions that are $\frac{1}{2}$ unit². The 6 triangles can be paired together to form 3 units². Altogether the area of the triangular region is (15+3) units², or 18 units².

Exercise: Multiple Volume Representations
The right pentagonal prism is composed of a right rectangular prism joined with a right triangular prism. Find the volume of the right pentagonal prism shown in the diagram using two different strategies.
$Engage NY Math Grade 7 Module 3 Lesson 23 Exercise Answer Key 3$
Answer:
Strategy #1
The volume of the pentagonal prism is equal to the sum of the volumes of the rectangular and triangular prisms.
V = V_{rectangular prism}+ V_{triangular prism}
V = Bh
V = (lw)h
V = (4 m ∙ 6 $\frac{1}{2}$ m) ∙ 6 $\frac{1}{2}$ m
V = (24 m²+2 m²) ∙ 6 $\frac{1}{2}$ m
V = 26 m² ∙ 6 $\frac{1}{2}$ m
V = 156 m³+13 m³
V = 169 m³

V = Bh
V = ($\frac{1}{2}$ lw)h
V = ($\frac{1}{2}$ ∙ 4 m ∙ $\frac{1}{2}$ m) ∙ 6 $\frac{1}{2}$ m
V = (2 m ∙ $\frac{1}{2}$ m) ∙ 6 $\frac{1}{2}$ m
V = (1 m² ) ∙ 6 $\frac{1}{2}$ m
V = 6 $\frac{1}{2}$ m³
So the total volume of the pentagonal prism is 169 m³+6 $\frac{1}{2}$ m³, or 175 $\frac{1}{2}$ m³ .

Strategy #2
The volume of a right prism is equal to the area of its base times its height. The base is a rectangle and a triangle.
V = Bh
B = A_rectangle+ A_triangle
A_rectangle = 4 m ∙ 6 $\frac{1}{2}$ m
A_rectangle = 24 m²+2 m²
A_rectangle = 26 m²

A_triangle = $\frac{1}{2}$ ∙ 4 m ∙ $\frac{1}{2}$ m
A_triangle = 2 m ∙ $\frac{1}{2}$ m
A_triangle = 1 m²

V = Bh
V = 27 m² ∙ 6 $\frac{1}{2}$ m
V = 162 m³+13 $\frac{1}{2}$ m³
V = 175 $\frac{1}{2}$ m³

B = 26 m²+1 m²
B = 27 m²
The volume of the right pentagonal prism is 175 $\frac{1}{2}$ m³.

Eureka Math Grade 7 Module 3 Lesson 23 Problem Set Answer Key

Question 1.
Calculate the volume of each solid using the formula V = Bh (all angles are 90 degrees).
a.
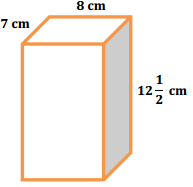
$Eureka Math 7th Grade Module 3 Lesson 23 Problem Set Answer Key 1$
Answer:
V = Bh
V = (8 cm ∙ 7 cm) ∙ 12 $\frac{1}{2}$ cm
V = (56 ∙ 12 $\frac{1}{2}$) cm³
V = 672 cm³+28 cm³
V = 700 cm³
The volume of the solid is 700 cm³.

b.
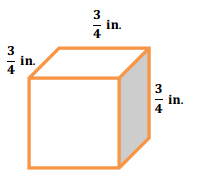
$Eureka Math 7th Grade Module 3 Lesson 23 Problem Set Answer Key 2$
Answer:
V = Bh
V = ($\frac{3}{4}$ in. ∙ $\frac{3}{4}$ in.) ∙ $\frac{3}{4}$ in.
V = (9/16) ∙ $\frac{3}{4}$ in³
V = $\frac{27}{64}$ in³
The volume of the cube is $\frac{27}{64}$ in³.

c.
$Eureka Math 7th Grade Module 3 Lesson 23 Problem Set Answer Key 3$
Answer:
V = Bh
B = A_rectangle+A_square
B = lw+s²
B = (2 $\frac{1}{2}$ in. ∙ 4 $\frac{1}{2}$ in.)+(1 $\frac{1}{2}$ in.)²
B = (10 in²+1 $\frac{1}{4}$ in² )+(1 $\frac{1}{2}$ in. ∙ 1 $\frac{1}{2}$ in.)
B = 11 $\frac{1}{4}$ in²+(1 $\frac{1}{2}$ in²+$\frac{3}{4}$ in² )
B = 11 $\frac{1}{4}$ in²+$\frac{3}{4}$ in²+1 $\frac{1}{2}$ in²
B = 12 in²+1 $\frac{1}{2}$ in²
B = 13 $\frac{1}{2}$ in²

V = Bh
V = 13 $\frac{1}{2}$ in² ∙ $\frac{1}{2}$ in.
V = $\frac{13}{2}$ in³+$\frac{1}{4}$ in³
V = 6 in³+$\frac{1}{2}$ in³+$\frac{1}{4}$ in³
V = 6 $\frac{3}{4}$ in³
The volume of the solid is 6 $\frac{3}{4}$ in³.

d.
$Eureka Math 7th Grade Module 3 Lesson 23 Problem Set Answer Key 4$
Answer:
V = Bh
B = (A_{(lg rectangle})-(A_{sm rectangle})
B = (lw)₁– (lw)₂
B = (6 yd. ∙ 4 yd.)-(1 $\frac{1}{3}$ yd. ∙ 2 yd.)
B = 24 yd²-(2 yd²+$\frac{2}{3}$ yd² )
B = 24 yd²-2 yd²–$\frac{2}{3}$ yd²
B = 22 yd²–$\frac{2}{3}$ yd²
B = 21 $\frac{1}{3}$ yd²

V = Bh
V = (21 $\frac{1}{3}$ yd²) ∙ $\frac{2}{3}$ yd.
V = 14 yd³+($\frac{1}{3}$ yd² ∙ $\frac{2}{3}$ yd.)
V = 14 yd³+$\frac{2}{9}$ yd³
V = 14 $\frac{2}{9}$ yd³
The volume of the solid is 14 $\frac{2}{9}$ yd³.

e.
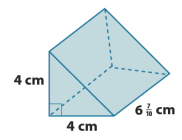
$Eureka Math 7th Grade Module 3 Lesson 23 Problem Set Answer Key 5$
Answer:
V = Bh_prism
B = $\frac{1}{2}$ bh_triangle
B = $\frac{1}{2}$ ∙ 4 cm ∙ 4 cm
B = 2 ∙ 4 cm²
B = 8 cm²

V = Bh
V = 8 cm² ∙ 6 $\frac{7}{10}$ cm
V = 48 cm³+$\frac{56}{10}$ cm³
V = 48 cm³+5 cm³+6/10 cm³
V = 53 cm³+$\frac{3}{5}$ cm³
V = 53 $\frac{3}{5}$ cm³
The volume of the solid is 53 $\frac{3}{5}$ cm³.

f.
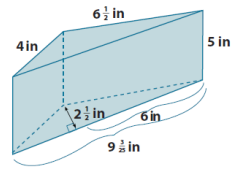
$Eureka Math 7th Grade Module 3 Lesson 23 Problem Set Answer Key 6$
Answer:
V = Bh_prism
B = $\frac{1}{2}$ bh_triangle
B = $\frac{1}{2}$ ∙ 9 $\frac{3}{25}$ in. ∙ 2 $\frac{1}{2}$ in.
B = $\frac{1}{2}$ ∙ 2 $\frac{1}{2}$ in. ∙ 9 3/25 in.
B = (1 $\frac{1}{4}$ ) ∙ (9 $\frac{3}{25}$ )in²
B = ($\frac{5}{4}$ ∙ $\frac{228}{25}$ )in²
B = $\frac{57}{5}$ in²

V = Bh
V = ($\frac{57}{5}$ in² ) ∙ 5 in
V = 57 in³
The volume of the solid is 57 in³.

g.
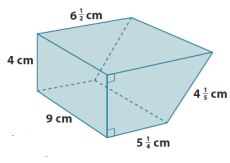
$Eureka Math 7th Grade Module 3 Lesson 23 Problem Set Answer Key 7$
Answer:
V = Bh
B = A_rectangle+ A_triangle
B = lw+$\frac{1}{2}$ bh
B = (5 $\frac{1}{4}$ cm ∙ 4 cm)+$\frac{1}{2}$ (4 cm ∙ 1 $\frac{1}{4}$ cm)
B = (20 cm²+1 cm² )+(2 cm ∙ 1 $\frac{1}{4}$ cm)
B = 21 cm²+2 cm²+$\frac{1}{2}$ cm²
B = 23 cm²+$\frac{1}{2}$ cm²
B = 23 $\frac{1}{2}$ cm²

V = Bh
V = 23 $\frac{1}{2}$ cm² ∙ 9 cm
V = 207 cm³+$\frac{9}{2}$ cm³
V = 207 cm³+4 cm³+$\frac{1}{2}$ cm³
V = 211 $\frac{1}{2}$ cm³
The volume of the solid is 211 $\frac{1}{2}$ cm³.

h.
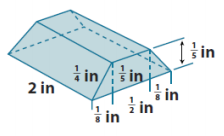
$Eureka Math 7th Grade Module 3 Lesson 23 Problem Set Answer Key 8$
Answer:
V = Bh
V = $\frac{1}{8}$ in² ∙ 2 in.
V = $\frac{1}{4}$ in³

B = A_rectangle+2A_triangle
B = lw+2 ∙ $\frac{1}{2}$ bh
B = ($\frac{1}{2}$ in. ∙ $\frac{1}{5}$ in.)+(1 ∙ $\frac{1}{8}$ in. ∙ $\frac{1}{5}$ in.)
B = $\frac{1}{10}$ in²+$\frac{1}{40}$ in²
B = $\frac{4}{40}$ in²+$\frac{1}{40}$ in²
The volume of the solid is $\frac{1}{4}$ in³.
B = $\frac{5}{40}$ in²
B = $\frac{1}{8}$ in²

Question 2.
Let l represent the length, w the width, and h the height of a right rectangular prism. Find the volume of the prism when
a. l = 3 cm, w = 2 $\frac{1}{2}$ cm, and h = 7 cm.
Answer:
V = lwh
V = 3 cm ∙ 2 $\frac{1}{2}$ cm ∙ 7 cm
V = 21 ∙ (2 $\frac{1}{2}$ ) cm³
V = 52 $\frac{1}{2}$ cm³ The volume of the prism is 52 $\frac{1}{2}$ cm³.

l = $\frac{1}{4}$ cm, w = 4 cm, and h = 1 $\frac{1}{2}$ cm.
V = lwh
V = $\frac{1}{4}$ cm ∙ 4 cm ∙ 1 $\frac{1}{2}$ cm
V = 1 $\frac{1}{2}$ cm³ The volume of the prism is 1 $\frac{1}{2}$ cm³.

Question 3.
Find the length of the edge indicated in each diagram.
a. V = Bh
Let h represent the number of inches in the height of the prism.
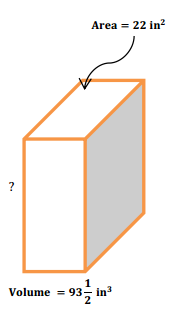
$Eureka Math 7th Grade Module 3 Lesson 23 Problem Set Answer Key 9$
93 $\frac{1}{2}$ in³ = 22 in² ∙ h
93 $\frac{1}{2}$ in³ = 22h in²
22h = 93.5 in
h = 4.25 in
The height of the right rectangular prism is 4 $\frac{1}{4}$ in.

What are possible dimensions of the base?
11 in by 2 in, or 22 in by 1 in

b. V = Bh
Let h represent the number of meters in the height of the triangular base of the prism.
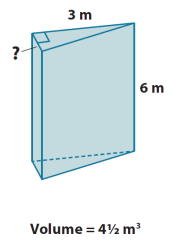
$Eureka Math 7th Grade Module 3 Lesson 23 Problem Set Answer Key 10$
V = ($\frac{1}{2}$ bh_triangle) ∙ h_prism
4 $\frac{1}{2}$ m³ = ($\frac{1}{2}$ ∙ 3 m ∙ h) ∙ 6 m
4 $\frac{1}{2}$ m³ = $\frac{1}{2}$ ∙ 18 m² ∙ h
4 $\frac{1}{2}$ m³ = 9h m²
9h = 4.5 m
h = 0.5 m
The height of the triangle is $\frac{1}{2}$ m.

Question 4.
The volume of a cube is 3 $\frac{3}{8}$ in³. Find the length of each edge of the cube.
Answer:
V = s³, and since the volume is a fraction, the edge length must also be fractional.
3 $\frac{3}{8}$ in³ = $\frac{27}{8}$ in³
3 $\frac{3}{8}$ in³ = $\frac{3}{2}$ in. ∙ $\frac{3}{2}$ in. ∙ $\frac{3}{2}$ in.
3 $\frac{3}{8}$ in³ = ($\frac{3}{2}$ in.)³
The lengths of the edges of the cube are $\frac{3}{2}$ in., or 1 $\frac{1}{2}$ in.

Question 5.
Given a right rectangular prism with a volume of 7 $\frac{1}{2}$ ft³, a length of 5 ft., and a width of 2 ft., find the height of the prism.
Answer:
V = Bh
V = (lw)h Let h represent the number of feet in the height of the prism.
7 $\frac{1}{2}$ ft³ = (5ft. ∙ 2ft.) ∙ h
7 $\frac{1}{2}$ ft³ = 10 ft² ∙ h
7.5 ft³ = 10h ft²
h = 0.75 ft.
The height of the right rectangular prism is $\frac{3}{4}$ ft. (or 9 in.).

Eureka Math Grade 7 Module 3 Lesson 23 Exit Ticket Answer Key

Question 1.
The base of the right prism is a hexagon composed of a rectangle and two triangles. Find the volume of the right hexagonal prism using the formula V = Bh.
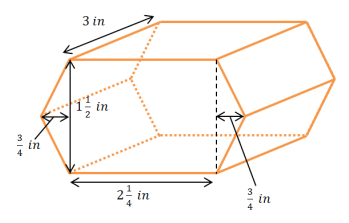
$Eureka Math Grade 7 Module 3 Lesson 23 Exit Ticket Answer Key 1$
Answer:
The area of the base is the sum of the areas of the rectangle and the two triangles.
B = A_rectangle+2 ∙ A_triangle
A_rectangle = lw
A_rectangle = 2 $\frac{1}{4}$ in. ∙ 1 $\frac{1}{2}$ in.
A_rectangle = ($\frac{9}{4}$ ∙ $\frac{3}{2}$) in²
A_rectangle = $\frac{27}{8}$ in²

A_triangle = $\frac{1}{2}$ lw
A_triangle = $\frac{1}{2}$ (1 $\frac{1}{2}$ in. ∙ $\frac{3}{4}$ in.)
A_triangle = ($\frac{1}{2}$ ∙ $\frac{3}{2}$ ∙ $\frac{3}{4}$ )in²
A_triangle = $\frac{9}{16}$ in²

B = $\frac{27}{8}$ in²+2($\frac{9}{16}$ in² )
B = $\frac{27}{8}$ in²+$\frac{9}{8}$ in²
B = $\frac{36}{8}$ in²
B = $\frac{9}{2}$ in²

V = Bh
V = ($\frac{9}{2}$ in² ) ∙ 3 in.
V = $\frac{27}{2}$ in³
V = 13 $\frac{1}{2}$ in³

The volume of the hexagonal prism is 13 $\frac{1}{2}$ in³.