Engage NY Eureka Math 7th Grade Module 3 Lesson 22 Answer Key
Eureka Math Grade 7 Module 3 Lesson 22 Example Answer Key
Example 1.
The pyramid in the picture has a square base, and its lateral faces are triangles that are exact copies of one another. Find the surface area of the pyramid.
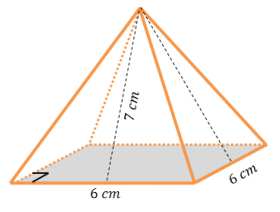
Answer:
The surface area of the pyramid consists of one square base and four lateral triangular faces.
B = s2
B = (6 cm)2
B = 36 cm2
The pyramid’s base area is 36 cm2.
LA = 4(\(\frac{1}{2}\) bh)
LA = 4 ∙ \(\frac{1}{2}\) (6 cm ∙ 7 cm)
LA = 2(6 cm ∙ 7 cm)
LA = 2(42 cm2 )
LA = 84 cm2
The pyramid’s lateral area is 84 cm2.
SA = LA + B
SA = 84 cm2 + 36 cm2
SA = 120 cm2
The surface area of the pyramid is 120 cm2.
Example 2: Using Cubes
There are 13 cubes glued together forming the solid in the diagram. The edges of each cube are \(\frac{1}{4}\) inch in length. Find the surface area of the solid.
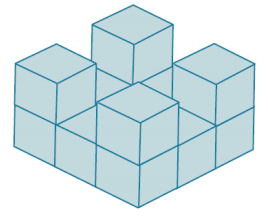
Answer:
The surface area of the solid consists of 46 square faces, all having side lengths of \(\frac{1}{4}\) inch. The area of a square having sides of length \(\frac{1}{4}\) inch is \(\frac{1}{16}\) in2 .
SA = 46 ∙ Asquare
SA = 46 ∙ \(\frac{1}{16}\) in2
SA = \(\frac{46}{16}\) in2
SA = 2 \(\frac{14}{16}\) in2
SA = 2 \(\frac{7}{8}\) in2 The surface are of the solid is 2 \(\frac{7}{8}\) in2.
Example 3.
Find the total surface area of the wooden jewelry box. The sides and bottom of the box are all \(\frac{1}{4}\) inch thick.
What are the faces that make up this box?
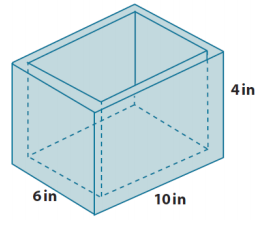
Answer:
The box has a rectangular bottom, rectangular lateral faces, and a rectangular top that has a smaller rectangle removed from it. There are also rectangular faces that make up the inner lateral faces and the inner bottom of the box.
How does this box compare to other objects that you have found the surface area of?
Answer:
The box is a rectangular prism with a smaller rectangular prism removed from its inside. The total surface area is equal to the surface area of the larger right rectangular prism plus the lateral area of the smaller right rectangular prism.
Large Prism: The surface area of the large right rectangular prism makes up the outside faces of the box, the rim of the box, and the inside bottom face of the box.
SA = LA + 2B
LA = P ∙ h
LA = 32 in. ∙ 4 in.
LA = 128 in2
B = lw
B = 10 in. ∙ 6 in.
B = 60 in2
The lateral area is 128 in2.
The base area is 60 in2.
SA = LA + 2B
SA = 128 in2 + 2(60 in2)
SA = 128 in2 + 120 in2
SA = 248 in2
The surface area of the larger prism is 248 in2.
Small Prism: The smaller prism is \(\frac{1}{2}\) in. smaller in length and width and \(\frac{1}{4}\) in. smaller in height due to the thickness of the sides of the box.
SA = LA + 1B
LA = P ∙ h
LA = 2(9 \(\frac{1}{2}\) in. + 5 \(\frac{1}{2}\) in.) ∙ 3 \(\frac{3}{4}\) in.
LA = 2(14 in. + 1 in.) ∙ 3 \(\frac{3}{4}\) in.
LA = 2(15 in.) ∙ 3 \(\frac{3}{4}\) in.
LA = 30 in. ∙ 3 \(\frac{3}{4}\) in.
LA = 90 in2 + \(\frac{90}{4}\) in2
LA = 90 in2 + 22 \(\frac{1}{2}\) in2
LA = 112 \(\frac{1}{2}\) in2
The lateral area is 112 \(\frac{1}{2}\) in2.
Surface Area of the Box
SAbox = SA + LA
SAbox = 248 in2 + 112 \(\frac{1}{2}\) in2
SAbox = 360 \(\frac{1}{2}\) in2
The total surface area of the box is 360 \(\frac{1}{2}\) in2.
Eureka Math Grade 7 Module 3 Lesson 22 Exercise Answer Key
Opening Exercise
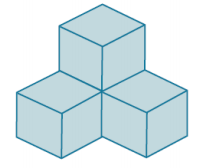
What is the area of the composite figure in the diagram? Is the diagram a net for a three-dimensional image? If so, sketch the image. If not, explain why.
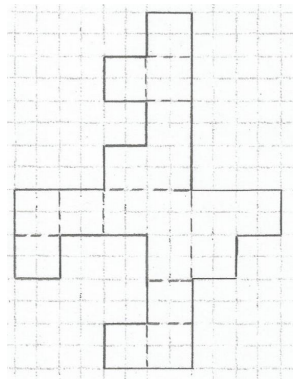
Answer:
There are four unit squares in each square of the figure. There are 18 total squares that make up the figure, so the total area of the composite figure is
A = 18 ∙ 4 units2 = 72 units2.
The composite figure does represent the net of a three-dimensional figure. The figure is shown below.
Eureka Math Grade 7 Module 3 Lesson 22 Problem Set Answer Key
Question 1.
For each of the following nets, draw (or describe) the solid represented by the net and find its surface area.
a. The equilateral triangles are exact copies.
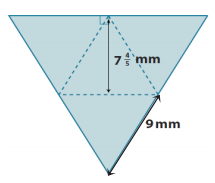
Answer:
The net represents a triangular pyramid where the three lateral faces are identical to each other and the triangular base.
SA = 4B since the faces are all the same size and shape.
SA = 4B
SA = 4(35 \(\frac{1}{10}\) mm2 )
SA = 140 mm2 + \(\frac{4}{10}\) mm2
SA = 140 \(\frac{2}{5}\) mm2
B = \(\frac{1}{2}\) bh
B = \(\frac{1}{2}\) ∙ 9 mm ∙ 7 \(\frac{4}{5}\) mm
B = \(\frac{9}{2}\) mm ∙ 7 \(\frac{4}{5}\) mm
B = \(\frac{63}{2}\) mm2 + \(\frac{36}{10}\) mm2
B = \(\frac{315}{10}\) mm2 + \(\frac{36}{10}\) mm2
B = \(\frac{351}{10}\) mm2 The surface area of the triangular pyramid is 140 \(\frac{2}{5}\) mm2.
B = 35 \(\frac{1}{10}\) mm2
b.
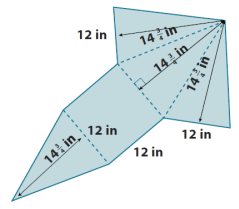
Answer:
The net represents a square pyramid that has four identical lateral faces that are triangles. The base is a square.
B = s2
B = (12 in.)2
B = 144 in2
LA = 2(12 in. ∙ 14 \(\frac{3}{4}\) in.)
SA = LA + B
LA = 4 ∙ \(\frac{1}{2}\) (bh)
LA = 4 ∙ \(\frac{1}{2}\) (12 in. ∙ 14 \(\frac{3}{4}\) in.)
LA = 2(168 in2 + 9 in2 )
LA = 336 in2 + 18 in2
LA = 354 in2
SA = LA + B
SA = 354 in2 + 144 in2
SA = 498 in2
The surface area of the square pyramid is 498 in2.
Question 2.
Find the surface area of the following prism.
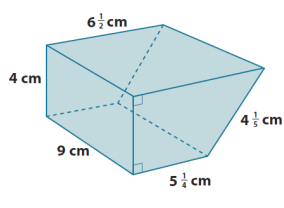
Answer:
SA = LA + 2B
LA = P ∙ h
LA = (4 cm + 6 \(\frac{1}{2}\) cm + 4 \(\frac{1}{5}\) cm + 5 \(\frac{1}{4}\) cm) ∙ 9 cm
LA = (19 cm + \(\frac{1}{2}\) cm + \(\frac{1}{5}\) cm + \(\frac{1}{4}\) cm) ∙ 9 cm
LA = (19 cm + \(\frac{10}{20}\) cm + \(\frac{4}{20}\) cm + \(\frac{5}{20}\) cm) ∙ 9 cm
LA = (19 cm + \(\frac{19}{20}\) cm) ∙ 9 cm
LA = 171 cm2 + \(\frac{171}{20}\) cm2
LA = 171 cm2 + 8 \(\frac{11}{20}\) cm2
LA = 179 \(\frac{11}{20}\) cm2
B = Arectangle + Atriangle
B = (5 \(\frac{1}{4}\) cm ∙ 4 cm) + \(\frac{1}{2}\)(4 cm ∙ 1 \(\frac{1}{4}\) cm)
B = (20 cm2 + 1 cm2 ) + (2 cm ∙ 1 \(\frac{1}{4}\) cm)
B = 21 cm2 + 2 \(\frac{1}{2}\) cm2
B = 23 \(\frac{1}{2}\) cm2
SA = LA + 2B
SA = 179 \(\frac{11}{20}\) cm2 + 2(23 \(\frac{1}{2}\) cm2 )
SA = 179 \(\frac{11}{20}\) cm2 + 47 cm2
SA = 226 \(\frac{11}{20}\) cm2
The surface area of the prism is 226 \(\frac{11}{20}\) cm2.
Question 3.
The net below is for a specific object. The measurements shown are in meters. Sketch (or describe) the object, and then find its surface area.
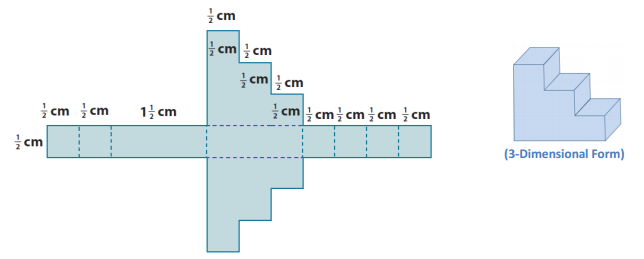
Answer:
SA = LA + 2B
LA = P ∙ h
LA = 6 cm ∙ \(\frac{1}{2}\) cm
LA = 3 cm2
B = (\(\frac{1}{2}\) cm ∙ \(\frac{1}{2}\) cm) + (\(\frac{1}{2}\) cm ∙ 1 cm) + (\(\frac{1}{2}\) cm ∙ 1 \(\frac{1}{2}\) cm)
B = (\(\frac{1}{4}\) cm2) + (\(\frac{1}{2}\) cm2 ) + (\(\frac{3}{4}\) cm2 )
B = (\(\frac{1}{4}\)cm2) + (\(\frac{2}{4}\) cm2) + (\(\frac{3}{4}\) cm2)
B = \(\frac{6}{4}\) cm2
B = 1 \(\frac{1}{2}\) cm2
SA = LA + 2B
SA = 3 cm2 + 2(1 \(\frac{1}{2}\) cm2 )
SA = 3 cm2 + 3 cm2
SA = 6 cm2
The surface area of the object is 6 cm2.
Question 4.
In the diagram, there are 14 cubes glued together to form a solid. Each cube has a volume of \(\frac{1}{8}\) in3. Find the surface area of the solid.
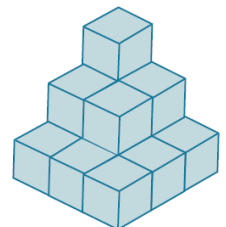
Answer:
The volume of a cube is s3, and 1/8 in3 is the same as (\(\frac{1}{2}\) in.)3, so the cubes have edges that are \(\frac{1}{2}\) in. long. The cube faces have area s2, or (\(\frac{1}{2}\) in.)2, or \(\frac{1}{4}\) in2. There are 42 cube faces that make up the surface of the solid.
SA = \(\frac{1}{4}\) in2 ∙ 42
SA = 10 \(\frac{1}{2}\) in2
The surface area of the solid is 10 \(\frac{1}{2}\) in2.
Question 5.
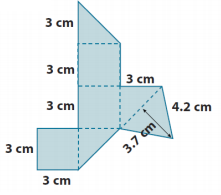
The nets below represent three solids. Sketch (or describe) each solid, and find its surface area.
a.
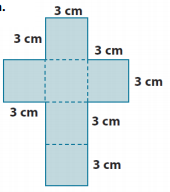
Answer:
SA = LA + 2B
LA = P ∙ h
LA = 12 ∙ 3
LA = 36 cm2
B = s2
B = (3 cm)2
B = 9 cm2
SA =
36 cm2 + 2(9 cm2)
SA = 36 cm2 + 18 cm2
SA = 54 cm2
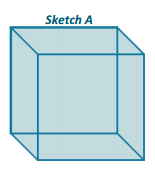
b.
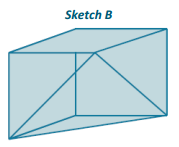
Answer:
SA = 3Asquare + 3Art triangle + Aequ triangle
Asquare = s2
Asquare = (3 cm)2
Asquare = 9 cm2
Art triangle = \(\frac{1}{2}\) bh
Art triangle = \(\frac{1}{2}\) ∙ 3 cm ∙ 3 cm
Art triangle = \(\frac{9}{2}\)
Art triangle = 4 \(\frac{1}{2}\) cm2
Aequ triangle = \(\frac{1}{2}\) bh
Aequ triangle = \(\frac{1}{2}\) ∙ (4 \(\frac{1}{5}\) cm) ∙ (3 \(\frac{7}{10}\) cm)
Aequ triangle = 2 \(\frac{1}{10}\) cm ∙ 3 \(\frac{7}{10}\) cm
Aequ triangle = \(\frac{21}{10}\) cm ∙ \(\frac{37}{10}\) cm
Aequ triangle = 7 \(\frac{77}{100}\) cm2
Aequ triangle = 7 \(\frac{77}{100}\) cm2
SA = 3(9 cm2 ) + 3(4 \(\frac{1}{2}\) cm2 ) + 7 \(\frac{77}{100}\) cm2
SA = 27 cm2 + (12 + \(\frac{3}{2}\)) cm2 + 7 \(\frac{77}{100}\) cm2
SA = 47 cm2 + \(\frac{1}{2}\) cm2 + \(\frac{77}{100}\) cm2
SA = 47 cm2 + \(\frac{50}{100}\) cm2 + \(\frac{77}{100}\) cm2
SA = 47 cm2 + \(\frac{127}{100}\) cm2
SA = 47 cm2 + 1 cm2 + \(\frac{27}{100}\) cm2
SA = 48 \(\frac{27}{100}\) cm2
c.
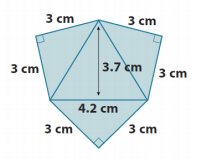
Answer:
SA = 3Art triangle + Aequ triangle
SA = 3(4 \(\frac{1}{2}\) ) cm2 + 7 \(\frac{77}{100}\) cm2
SA = 12 cm2 + \(\frac{3}{2}\) cm2 + 7 cm2 + \(\frac{77}{100}\) cm2
SA = 20 cm2 + \(\frac{1}{2}\) cm2 + \(\frac{77}{100}\) cm2
SA = 20 cm2 + 1 cm2 + \(\frac{27}{100}\) cm2
SA = 21 \(\frac{27}{100}\) cm2
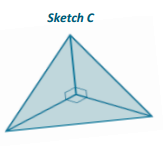
d. How are figures (b) and (c) related to figure (a)?
Answer:
If the equilateral triangular faces of figures (b) and (c) were matched together, they would form the cube in part (a).
Question 6.
Find the surface area of the solid shown in the diagram. The solid is a right triangular prism (with right triangular bases) with a smaller right triangular prism removed from it.
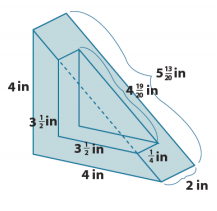
Answer:
SA = LA + 2B
LA = P ∙ h
LA = (4 in. + 4 in. + 5 \(\frac{13}{20}\) in.) ∙ 2 in.
LA = (13 \(\frac{13}{20}\) in.) ∙ 2 in.
LA = 26 in2 + \(\frac{13}{10}\) in2
LA = 26 in2 + 1 in2 + \(\frac{3}{10}\) in2
LA = 27 \(\frac{3}{10}\) in2
The \(\frac{1}{4}\)in. by 4 \(\frac{19}{20}\) in. rectangle has to be taken away from the lateral area:
A = lw
A = 4 \(\frac{19}{20}\) in ∙ \(\frac{1}{4}\) in
A = 1 in2 + 19/80 in2
A = 1 19/80 in2
LA = 27 \(\frac{3}{10}\) in2-1 \(\frac{19}{80}\) in2
LA = 27 \(\frac{24}{80}\) in2-1 \(\frac{19}{80}\) in2
LA = 26 \(\frac{5}{80}\) in2
LA = 26 \(\frac{1}{16}\) in2
Two bases of the larger and smaller triangular prisms must be added:
SA = 26 \(\frac{1}{16}\) in2 + 2(3 \(\frac{1}{2}\) in ∙ \(\frac{1}{4}\) in) + 2(\(\frac{1}{2}\) ∙ 4 in ∙ 4 in)
SA = 26 \(\frac{1}{16}\) in2 + 2 ∙ \(\frac{1}{4}\) in ∙ 3 \(\frac{1}{2}\) in + 16 in2
SA = 26 \(\frac{1}{16}\) in2 + \(\frac{1}{2}\) in ∙ 3 \(\frac{1}{2}\) in + 16 in2
SA = 26 \(\frac{1}{16}\) in2 + (\(\frac{3}{2}\) in2 + \(\frac{1}{4}\) in2 ) + 16 in2
SA = 26 \(\frac{1}{16}\) in2 + 1 in2 + \(\frac{8}{16}\) in2 + \(\frac{4}{16}\) in2 + 16 in2
SA = 43 \(\frac{13}{16}\) in2
The surface area of the solid is 43 \(\frac{13}{16}\) in2.
Question 7.
The diagram shows a cubic meter that has had three square holes punched completely through the cube on three perpendicular axes. Find the surface area of the remaining solid.
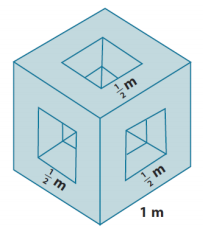
Answer:
Exterior surfaces of the cube (SA1):
SA1 = 6(1 m)2-6(\(\frac{1}{2}\) m)2
SA1 = 6(1 m2 )-6(\(\frac{1}{4}\) m2)
SA1 = 6 m2–\(\frac{6}{4}\) m2
SA1 = 6 m2-(1 \(\frac{1}{2}\) m2)
SA1 = 4 \(\frac{1}{2}\) m2
Just inside each square hole are four intermediate surfaces that can be treated as the lateral area of a rectangular prism. Each has a height of \(\frac{1}{4}\) m and perimeter of \(\frac{1}{2}\) m + \(\frac{1}{2}\) m + \(\frac{1}{2}\) m + \(\frac{1}{2}\) m or 2 m.
SA2 = 6(LA)
SA2 = 6(2 m ∙ \(\frac{1}{4}\) m)
SA2 = 6 ∙ \(\frac{1}{2}\) m2
SA2 = 3 m2
The total surface area of the remaining solid is the sum of these two areas:
SAT = SA1 + SA2.
SAT = 4 \(\frac{1}{2}\) m2 + 3 m2
SAT = 7 \(\frac{1}{2}\) m2
The surface area of the remaining solid is 7 \(\frac{1}{2}\) m2.
Eureka Math Grade 7 Module 3 Lesson 22 Exit Ticket Answer Key
Question 1.
The right hexagonal pyramid has a hexagon base with equal-length sides. The lateral faces of the pyramid are all triangles (that are exact copies of one another) with heights of 15 ft. Find the surface area of the pyramid.
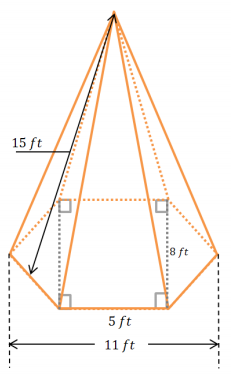
Answer:
SA = LA + 1B
LA = 6 ∙ \(\frac{1}{2}\) (bh)
LA = 6 ∙ \(\frac{1}{2}\) (5 ft. ∙ 15 ft.)
LA = 3 ∙ 75 ft2
LA = 225 ft2
B = Arectangle + 2Atriangle
B = (8 ft. ∙ 5 ft.) + 2 ∙ \(\frac{1}{2}\) (8 ft. ∙ 3 ft.)
B = 40 ft2 + (8 ft. ∙ 3 ft.)
B = 40 ft2 + 24 ft2
B = 64 ft2
SA = LA + 1B
SA = 225 ft2 + 64 ft2
SA = 289 ft2
The surface area of the pyramid is 289 ft2.
Question 2.
Six cubes are glued together to form the solid shown in the diagram. If the edges of each cube measure 1 \(\frac{1}{2}\) inches in length, what is the surface area of the solid?
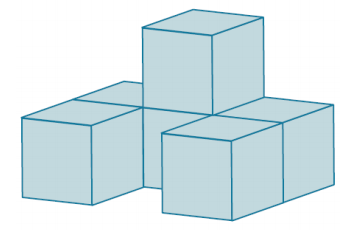
Answer:
There are 26 square cube faces showing on the surface area of the solid (5 each from the top and bottom view, 4 each from the front and back view, 3 each from the left and right side views, and 2 from the “inside” of the front).
A = s2
A = (1 \(\frac{1}{2}\) in.)2
A = (1 \(\frac{1}{2}\) in.)(1 \(\frac{1}{2}\) in.)
A = 1 \(\frac{1}{2}\) in.(1 in. + \(\frac{1}{2}\) in.)
A = (1 \(\frac{1}{2}\) in. ∙ 1 in.) + (1 \(\frac{1}{2}\) in. ∙ \(\frac{1}{2}\) in.)
A = 1 \(\frac{1}{2}\) in2 + \(\frac{3}{4}\) in2
A = 1 \(\frac{2}{4}\) in2 + \(\frac{3}{4}\) in2
A = 1 \(\frac{5}{4}\) in2 = 2 \(\frac{1}{4}\) in2
SA = 26 ∙ (2 \(\frac{1}{4}\) in2)
SA = 52 in2 + \(\frac{26}{4}\) in2
SA = 52 in2 + 6 in2 + \(\frac{1}{2}\) in2
SA = 58 \(\frac{1}{2}\) in2
The surface area of the solid is 58 \(\frac{1}{2}\) in2.