Engage NY Eureka Math 7th Grade Module 3 Lesson 12 Answer Key
Eureka Math Grade 7 Module 3 Lesson 12 Example Answer Key
Example 1.
Preserves the inequality symbol:
Answer:
means the inequality symbol stays the same.
Reverses the inequality symbol:
Answer:
means the inequality symbol switches less than with greater than and less than or equal to with greater than or equal to.
Station 1
Add or Subtract a Number to Both Sides of the Inequality
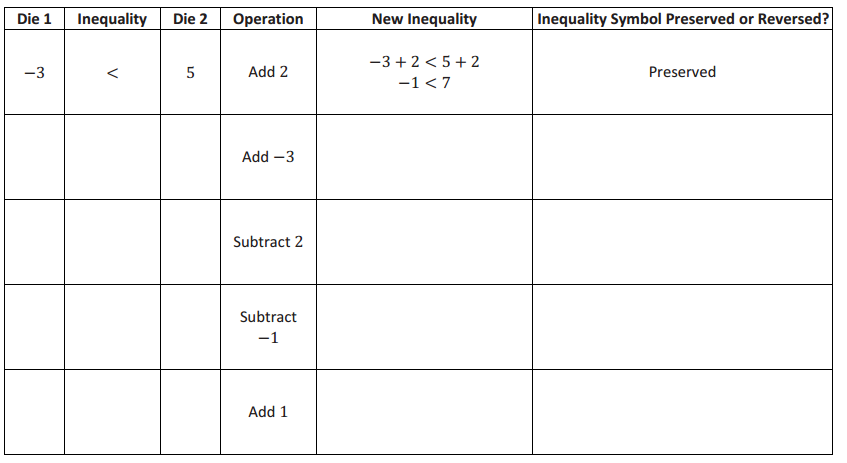
Examine the results. Make a statement about what you notice, and justify it with evidence.
Answer:
When a number is added or subtracted to both numbers being compared, the symbol stays the same, and the inequality symbol is preserved.
Station 2
Multiply each term by – 1
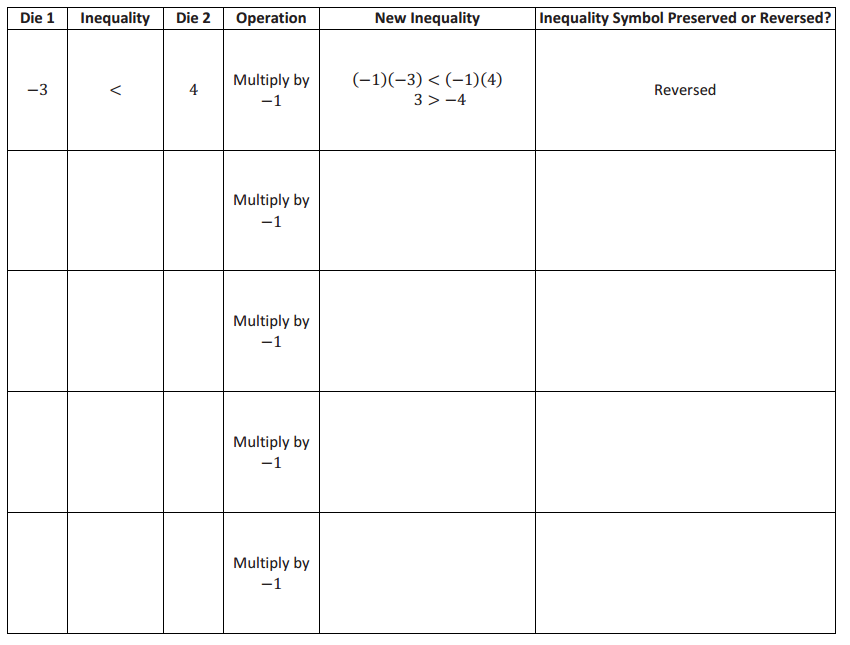
Examine the results. Make a statement about what you notice and justify it with evidence.
Answer:
When both numbers are multiplied by – 1, the symbol changes, and the inequality symbol is reversed.
Station 3
Multiply or Divide Both Sides of the Inequality by a Positive Number
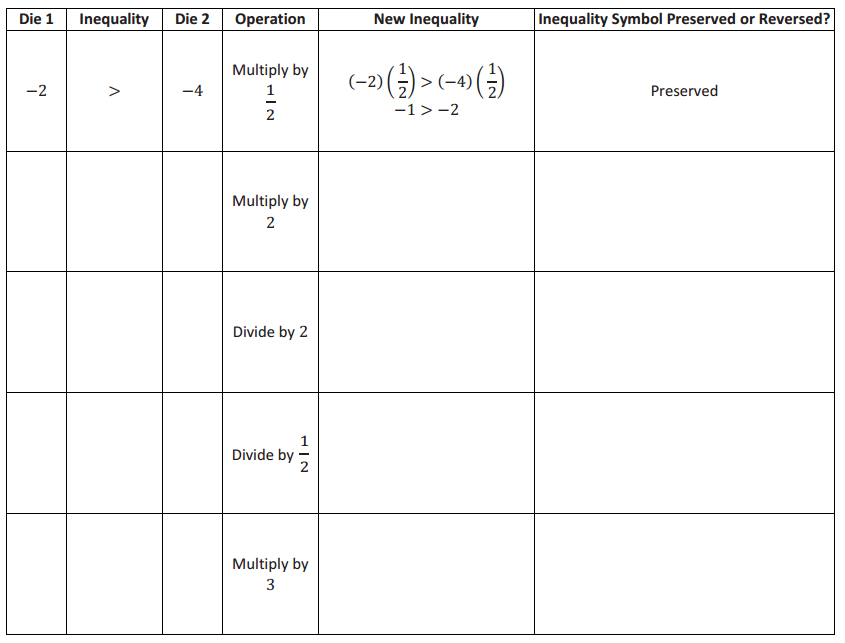
Examine the results. Make a statement about what you notice, and justify it with evidence.
Answer:
When both numbers being compared are multiplied by or divided by a positive number, the symbol stays the same, and the inequality symbol is preserved.
Station 4
Multiply or Divide Both Sides of the Inequality by a Negative Number
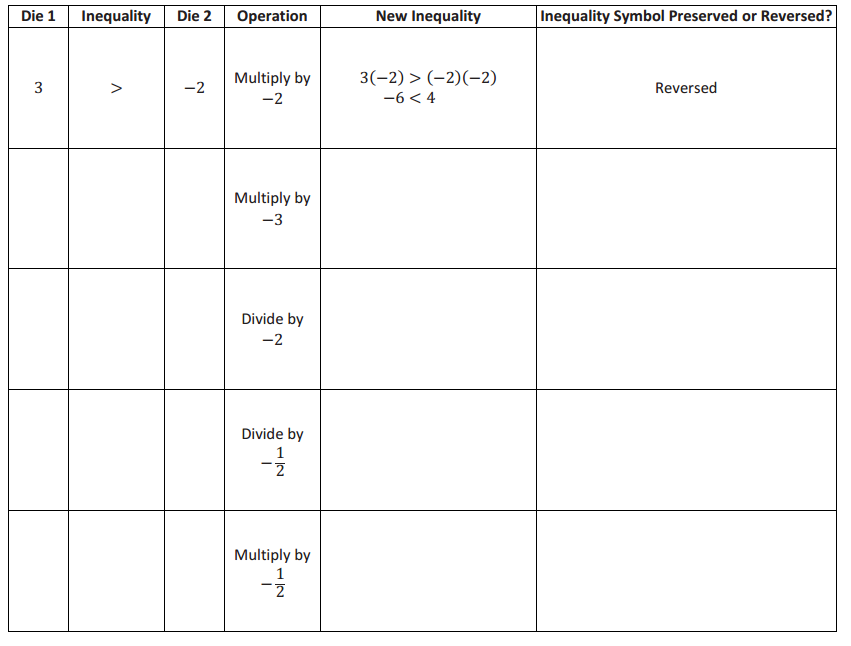
Examine the results. Make a statement about what you notice and justify it with evidence.
Answer:
When both numbers being compared are multiplied by or divided by a negative number, the symbol changes, and the inequality symbol is reversed.
Eureka Math Grade 7 Module 3 Lesson 12 Exercise Answer Key
Exercise
Complete the following chart using the given inequality, and determine an operation in which the inequality symbol is preserved and an operation in which the inequality symbol is reversed. Explain why this occurs.
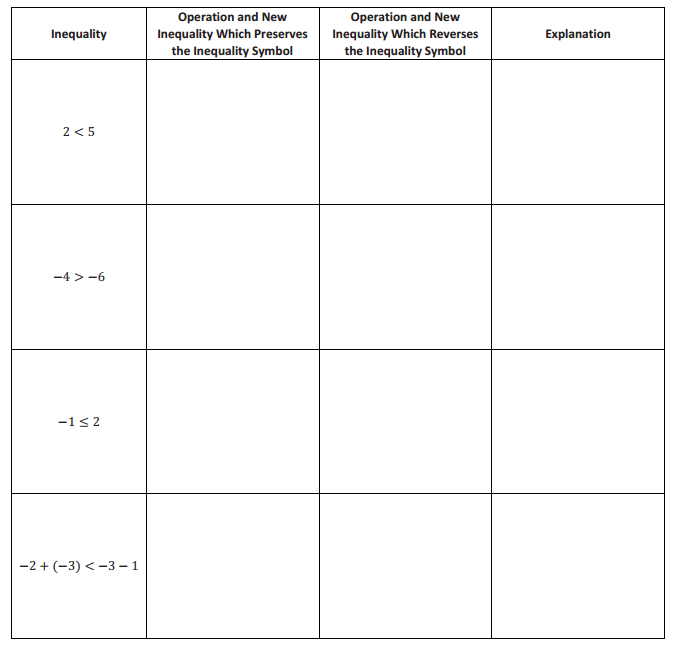
Answer:
Solutions may vary. A sample student response is below.
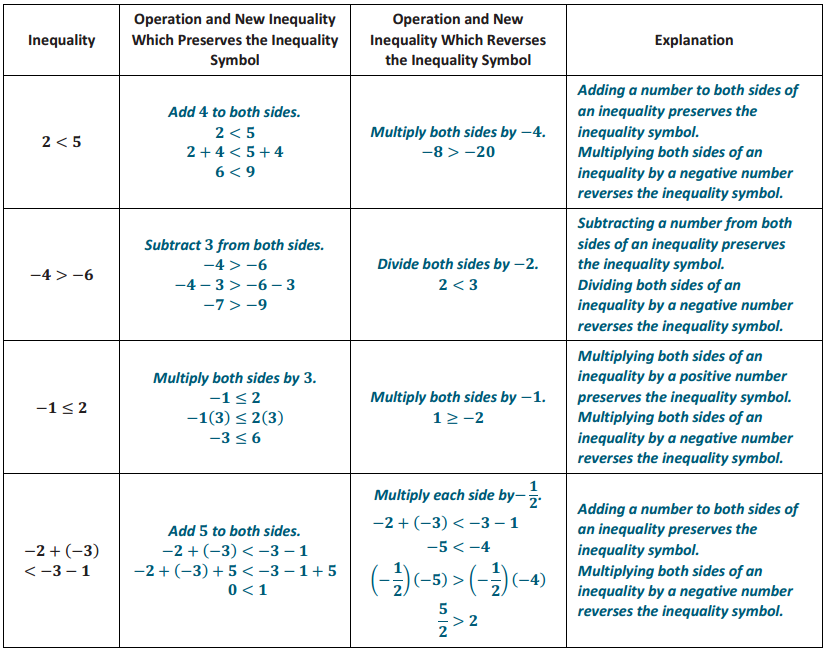
Eureka Math Grade 7 Module 3 Lesson 12 Problem Set Answer Key
Question 1.
For each problem, use the properties of inequalities to write a true inequality statement.
The two integers are – 2 and – 5.
a. Write a true inequality statement.
Answer:
– 5 < – 2
b. Subtract – 2 from each side of the inequality. Write a true inequality statement.
Answer:
– 7 < – 4
c. Multiply each number by – 3. Write a true inequality statement.
Answer:
15 > 6
Question 2.
On a recent vacation to the Caribbean, Kay and Tony wanted to explore the ocean elements. One day they went in a submarine 150 feet below sea level. The second day they went scuba diving 75 feet below sea level.
a. Write an inequality comparing the submarine’s elevation and the scuba diving elevation.
Answer:
– 150 < – 75
b. If they only were able to go one – fifth of the capable elevations, write a new inequality to show the elevations they actually achieved.
Answer:
– 30 < – 15
c. Was the inequality symbol preserved or reversed? Explain.
Answer:
The inequality symbol was preserved because the number that was multiplied to both sides was NOT negative.
Question 3.
If a is a negative integer, then which of the number sentences below is true? If the number sentence is not true, give a reason.
a. 5 + a < 5
Answer:
True
b. 5 + a > 5
Answer:
False because adding a negative number to 5 will decrease 5, which will not be greater than 5.
c. 5 – a > 5
Answer:
True
d. 5 – a < 5
Answer:
False because subtracting a negative number is adding a positive number to 5, which will be larger than 5.
e. 5a < 5
Answer:
True
f. 5a > 5
Answer:
False because a negative number multiplied by a positive number is negative, which will be less than 5.
g. 5 + a > a
Answer:
True
h. 5 + a < a
Answer: False because adding 5 to a negative number is greater than the negative number itself.
i. 5 – a > a
Answer:
True
j. 5 – a < a
Answer:
False because subtracting a negative number is the same as adding a positive number, which is greater than the negative number itself.
k. 5a > a
Answer:
False because a negative number multiplied by a 5 is negative and will be 5 times smaller than a.
l. 5a < a
Answer:
True
Eureka Math Grade 7 Module 3 Lesson 12 Exit Ticket Answer Key
Question 1.
Given the initial inequality – 4 < 7, state possible values for c that would satisfy the following inequalities.
a. c( – 4) < c(7)
Answer:
c > 0
b. c( – 4) > c(7)
Answer:
c < 0
c. c(- 4) = c(7)
Answer:
c = 0
Question 2.
Given the initial inequality 2 > – 4, identify which operation preserves the inequality symbol and which operation reverses the inequality symbol. Write the new inequality after the operation is performed.
a. Multiply both sides by – 2.
Answer:
The inequality symbol is reversed.
2 > – 4
2( – 2) < – 4( – 2)
– 4 < 8
b. Add – 2 to both sides.
Answer:
The inequality symbol is preserved. 2 > – 4
2 + ( – 2) > – 4 + ( – 2)
0 > – 6
c. Divide both sides by 2.
Answer:
The inequality symbol is preserved.
2 > – 4
2 ÷ 2 > – 4 ÷ 2
1 > – 2
d. Multiply both sides by – \(\frac{1}{2}\).
Answer:
Inequality symbol is reversed.
2 > – 4
2( – \(\frac{1}{2}\) ) < – 4( – \(\frac{1}{2}\) )
– 1 < 2 e. Subtract – 3 from both sides. Answer: The inequality symbol is preserved. 2 > – 4
2 – ( – 3) > – 4 – ( – 3)
5 > – 1
Eureka Math Grade 7 Module 3 Lesson 12 Equations Answer Key
Progression of Exercises
Determine the value of the variable.
Set 1
Question 1.
x + 1 = 5
Answer:
x = 4
Question 2.
x + 3 = 5
Answer:
x = 2
Question 3.
x + 6 = 5
Answer:
x = – 1
Question 4.
x – 5 = 2
Answer:
x = 7
Question 5.
x – 5 = 8
Answer:
x = 13
Set 2
Question 1.
3x = 15
Answer:
x = 5
Question 2.
3x = 0
Answer:
x = 0
Question 3.
3x = – 3
Answer:
x = – 1
Question 4.
– 9x = 18
Answer:
x = – 2
Question 5.
– x = 18
Answer:
x = – 18
Set 3
Question 1.
\(\frac{1}{7}\) x = 5
Answer:
x = 35
Question 2.
\(\frac{2}{7}\) x = 10
Answer:
x = 35
Question 3.
\(\frac{3}{7}\) x = 15
Answer:
x = 35
Question 4.
\(\frac{4}{7}\) x = 20
Answer:
x = 35
Question 5.
– \(\frac{5}{7}\) x = – 25
Answer:
x = 35
Set 4
Question 1.
2x + 4 = 12
Answer:
x = 4
Question 2.
2x – 5 = 13
Answer:
x = 9
Question 3.
2x + 6 = 14
Answer:
x = 4
Question 4.
3x – 6 = 18
Answer:
x = 8
Question 5.
– 4x + 6 = 22
Answer:
x = – 4
Set 5
Question 1.
2x + 0.5 = 6.5
Answer:
x = 3
Question 2.
3x – 0.5 = 8.5
Answer:
x = 3
Question 3.
5x + 3 = 8.5
Answer:
x = 1.1
Question 4.
5x – 4 = 1.5
Answer:
x = 1.1
Question 5.
– 7x + 1.5 = 5
Answer:
x = – 0.5
Set 6
Question 1.
2(x + 3) = 4
Answer:
x = – 1
Question 2.
5(x + 3) = 10
Answer:
x = – 1
Question 3.
5(x – 3) = 10
Answer:
x = 5
Question 4.
– 2(x – 3) = 8
Answer:
x = – 1
Question 5.
– 3(x + 4) = 3
Answer:
x = – 5