Engage NY Eureka Math 7th Grade Module 2 Lesson 12 Answer Key
Eureka Math Grade 7 Module 2 Lesson 12 Example Answer Key
Example 1.
Transitioning from Integer Multiplication Rules to Integer Division Rules
Students make an integer multiplication facts bubble by expanding upon the four related math facts they wrote down.
Step 1: Students construct three similar integer multiplication problems, two problems using one negative number as a factor and one with both negative numbers as factors. Students may use the commutative property to extend their three equations to six.
Record your group’s number sentences in the space on the left below.
Answer:
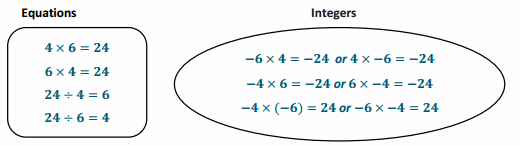
Step 2: Students use the integer multiplication facts in their integer bubble to create six related integer division facts. Group members should discuss the inverse relationship and the resulting division fact that must be true based on each multiplication equation.
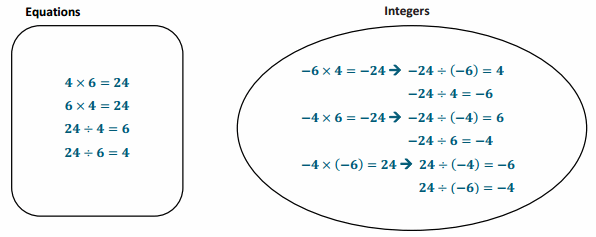
Step 3: Students use the equations in their integer bubble and the patterns they observed to answer the following questions.
a. List examples of division problems that produced a quotient that is a negative number.
Answer:
-24 ÷ 4 = -6 ; -24 ÷ 6 = -4 ; 24 ÷ (-4) = -6 ; 24 ÷ (-6) = -4
b. If the quotient is a negative number, what must be true about the signs of the dividend and divisor?
Answer:
The quotient is a negative number when the signs of the dividend and divisor are not the same; one is positive, and one is negative.
c. List your examples of division problems that produced a quotient that is a positive number.
Answer:
-24 ÷ (-4) = 6 ; -24 ÷ (-6) = 4 ; 24 ÷ 4 = 6 ; 24 ÷ 6 = 4
d. If the quotient is a positive number, what must be true about the signs of the dividend and divisor?
Answer:
The quotient is a positive number when the signs of the dividend and the divisor are the same in each case.
Step 4: Whole-group discussion. Students share answers from Step 3 with the class. The class comes to a consensus and realizes that since multiplication and division are related* (inverse operations), the integer rules for these operations are related. Students summarize the rules for division, which are stated in the Lesson Summary of the student materials. (*Reminder: The rules apply to all situations except dividing by zero.)
Rules for Dividing Two Integers:
→ A quotient is negative if the divisor and the dividend have __ signs.
Answer:
opposite
→ A quotient is positive if the divisor and the dividend have __ signs.
Answer:
the same
Eureka Math Grade 7 Module 2 Lesson 12 Exercise Answer Key
Exercise 2.
Is the Quotient of Two Integers Always an Integer?
Is the quotient of two integers always an integer? Use the work space below to create quotients of integers. Answer the question, and use examples or a counterexample to support your claim.
Work Space:
Answer:
-24 ÷ 6 = -4 Example of an integer quotient
6 ÷ (-24) = \(\frac{6}{-24}\) = \(\frac{1}{-4}\) = –\(\frac{1}{4}\) Counterexample: has a non-integer quotient
Answer:
No, quotients of integers are not always integers. In my first example above, -24 ÷ 6 yields an integer quotient -4. However, when I switched the divisor and dividend, that quotient divides a number with a smaller absolute value by a number with a greater absolute value, making the quotient a rational number between -1 and 1. In dividing 6 ÷ (-24), the quotient is \(\frac{6}{-24}\) = \(\frac{1}{-4}\). Of course, –\(\frac{1}{4}\) is not an integer but is the opposite value of the fraction \(\frac{1}{4}\). This counterexample shows that quotients of integers are not always integers.
Conclusion: Every quotient of two integers is always a rational number but not always an integer.
Once students have disproved the statement with a counterexample (where the quotient is a decimal or fraction), ask students to determine what must be true of two integers if their quotient is an integer. Students may need some time to study the examples where the quotient is an integer to determine that the quotient of two integers, \(\frac{A}{B}[/latex, B≠0, is an integer when either B = 1 or A = kB for any integer k.
Exercise 3.
Different Representation of the Same Quotient
Are the answers to the three quotients below the same or different? Why or why not?
a. -14 ÷ 7
Answer:
-14 ÷ 7 = -2
b. 14 ÷ (-7)
Answer:
14 ÷ (-7) = -2
c. -(14 ÷ 7)
Answer:
-(14 ÷ 7) = -(2) = -2
The answers to the problems are the same: -2. In part (c), the negative in front of the parentheses changes the value inside the parentheses to its opposite. The value in the parentheses is 2, and the opposite of 2 is -2.
Eureka Math Grade 7 Module 2 Lesson 12 Problem Set Answer Key
Question 1.
Find the missing values in each column.
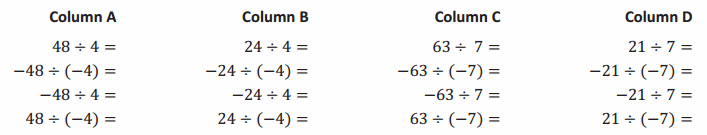
Answer:
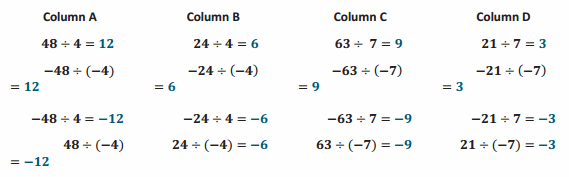
Question 2.
Describe the pattern you see in each column’s answers in Problem 1, relating it to the problems’ divisors and dividends. Why is this so?
Answer:
The pattern in the columns’ answers is the same two positive values followed by the same two negative values. This is so for the first two problems because the divisor and the dividend have the same signs and absolute values, which yields a positive quotient. This is so for the second two problems because the divisor and dividend have different signs but the same absolute values, which yields a negative quotient.
Question 3.
Describe the pattern you see between the answers for Columns A and B in Problem 1 (e.g., compare the first answer in Column A to the first answer in Column B; compare the second answer in Column A to the second answer in Column B). Why is this so?
Answer:
The answers in Column B are each one-half of the corresponding answers in Column A. That is because the dividend of 48 in Column A is divided by 4, and the dividend of 24 in Column B is divided by 4 (and so on with the same order and same absolute values but different signs). Since 24 is half of 48, the quotient (answer) in Column B will be one-half of the quotient in Column A.
Question 4.
Describe the pattern you see between the answers for Columns C and D in Problem 1. Why is this so?
Answer:
The answers in Column D are each one-third of the corresponding answers in Column C. That is because the dividend of 63 in Column C is divided by 7, and the dividend of 21 in Column D is divided by 7 (and so on with the same order and same absolute values but different signs). Since 21 is one-third of 63, the quotient (answer) in Column D will be one-third of the quotient in Column C.
Eureka Math Grade 7 Module 2 Lesson 12 Fluency Exercise: Integer Division Answer Key
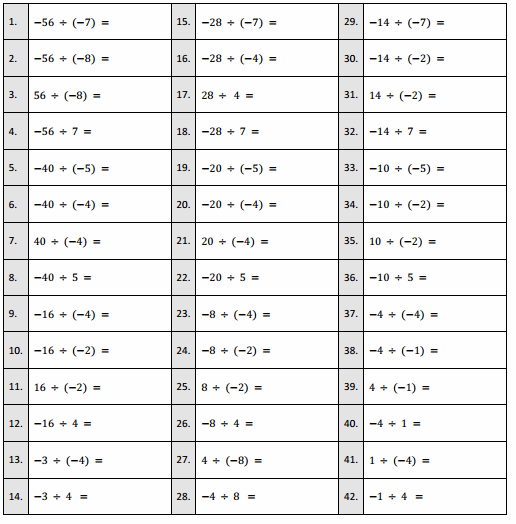
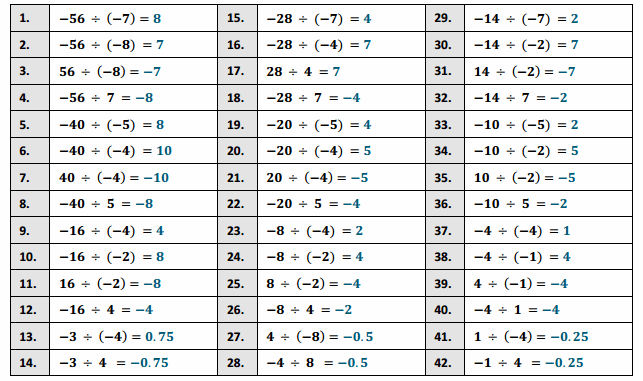
Answer:
Question 1.
-56 ÷ (-7) =
Answer:
8
Question 2.
-56 ÷ (-8) =
Answer:
7
Question 3.
56 ÷ (-8) =
Answer:
-7
Question 4.
-56 ÷ 7 =
Answer:
-8
Question 5.
-40 ÷ (-5) =
Answer:
8
Question 6.
-40 ÷ (-4) =
Answer:
10
Question 7.
40 ÷ (-4) =
Answer:
-10
Question 8.
-40 ÷ 5 =
Answer:
-8
Question 9.
-16 ÷ (-4) =
Answer:
4
Question 11.
-16 ÷ (-2) =
Answer:
8
Question 12.
16 ÷ (-2) =
Answer:
-8
Question 13.
-16 ÷ 4 =
Answer:
-4
Question 14.
-3 ÷ (-4) =
Answer:
0.75
Question 15.
-3 ÷ 4 =
Answer:
-0.75
Question 16.
-28 ÷ (-7) =
Answer:
4
Question 17.
-28 ÷ (-4) =
Answer:
7
Question 18.
28 ÷ 4 =
Answer:
7
Question 19.
-28 ÷ 7 =
Answer:
-4
Question 20.
-20 ÷ (-5) =
Answer:
4
Question 21.
-20 ÷ (-4) =
Answer:
5
Question 22.
20 ÷ (-4) =
Answer:
-5
Question 23.
-20 ÷ 5 =
Answer:
-4
Question 34.
-8 ÷ (-4) =
Answer:
2
Question 35.
-8 ÷ (-2) =
Answer:
4
Question 36.
8 ÷ (-2) =
Answer:
-4
Question 37.
-8 ÷ 4 =
Answer:
-2
Question 38.
4 ÷ (-8)=
Answer:
-0.5
Question 39.
-4 ÷ 8 =
Answer:
-0.5
Question 40.
-14 ÷ (-7) =
Answer:
2
Question 41.
-14 ÷ (-2) =
Answer:
7
Question 42.
14 ÷ (-2)=
Answer:
-7
Question 43.
-14 ÷ 7 =
Answer:
-2
Question 44.
-10 ÷ (-5) =
Answer:
2
Question 45.
-10 ÷ (-2) =
Answer:
5
Question 46.
10 ÷ (-2)=
Answer:
-5
Question 47.
-10 ÷ 5 =
Answer:
-2
Question 48.
-4 ÷ (-4) =
Answer:
1
Question 49.
-4 ÷ (-1) =
Answer:
4
Question 50.
4 ÷ (-1) =
Answer:
-4
Question 51.
-4 ÷ 1 =
Answer:
-4
Question 52.
1 ÷ (-4)=
Answer:
-0.25
Question 53.
-1 ÷ 4 =
Answer:
-0.25
Eureka Math Grade 7 Module 2 Lesson 12 Exit Ticket Answer Key
Question 1.
Mrs. McIntire, a seventh-grade math teacher, is grading papers. Three students gave the following responses to the same math problem:
Student one: [latex]\frac{1}{-2}\)
Student two: -(\(\frac{1}{2}\))
Student three: –\(\frac{1}{2}\)
On Mrs. McIntire’s answer key for the assignment, the correct answer is -0.5. Which student answer(s) is (are) correct? Explain.
Answer:
All student answers are correct since they are all equivalent to -0.5.
For student one: \(\frac{1}{-2}\) means 1 divided by -2. When dividing a positive 1 by a negative 2, the answer will be negative five-tenths or -0.5.
For student two: -(\(\frac{1}{2}\)) means the opposite of \(\frac{1}{2}\). One-half is equivalent to five-tenths, and the opposite is negative five-tenths or -0.5.
For student three: –\(\frac{1}{2}\) means -1 divided by 2. When dividing a negative 1 by a positive 2, the answer will be negative five-tenths or -0.5.
Question 2.
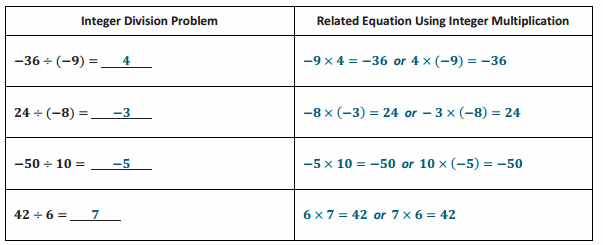
Complete the table below. Provide an answer for each integer division problem, and write a related equation using integer multiplication.
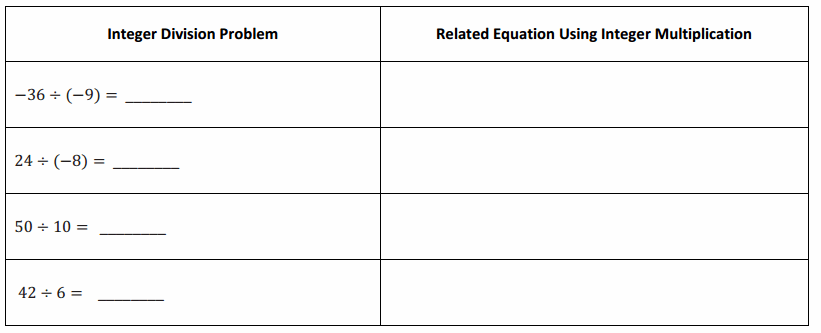
Answer: