Engage NY Eureka Math 7th Grade Module 2 End of Module Assessment Answer Key
Eureka Math Grade 7 Module 2 End of Module Assessment Task Answer Key
Question 1.
The water level in Ricky Lake changes at an average of –\(\frac{7}{16}\) inch every 3 years.
a. Based on the rate above, how much will the water level change after one year? Show your calculations and model your answer on the vertical number line, using 0 as the original water level.

Answer:

b. How much would the water level change over a 7-year period?
Answer:
Distance = rate × time
= – \(\frac{7}{48}\) × 7
= –\(\frac{49}{48}\)
= -1\(\frac{1}{48}\)
The water level drops 1\(\frac{1}{48}\) inches over a 7-year period.
c. When written in decimal form, is your answer to part (b) a repeating decimal or a terminating decimal? Justify your answer using long division.
Answer:
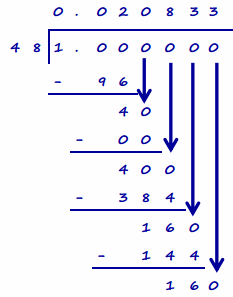
-1\(\frac{1}{48}\) written in decimal form is a repeating decimal because when converted using long division, the remainder repeats after the hundred-thousandths place.
Question 2.
Kay’s mother taught her how to make handmade ornaments to sell at a craft fair. Kay rented a table at the fair for $30 and set up her work station. Each ornament that she makes costs approximately $2.50 for materials. She sells each ornament for $6.00.
a. If x represents the number of ornaments sold at the craft fair, which of the following expressions would represent Kay’s profit? (Circle all choices that apply.)
A. -30 + 6x – 2.50x
B. 6x – 30 – 2.50x
C. 6x – 30
D. 4.50x-30
E. 3.50x-30
Answer:

b. Kay does not want to lose money on her business. Her mother told her she needs to sell enough ornaments to at least cover her expenses (costs for materials and table rental). Kay figures that if she sells 8 ornaments, she covers her expenses and does not lose any money. Do you agree? Explain and show work to support your answer.
Answer:
3.50x – 30
3.50(8) – 30
(24 + 4) – 30
28 – 30
-2
I disagree with Kay because selling 8 ornaments covers most of her costs but still leaves her $2 in debt.
c. Kay feels that if she earns a profit of $40.00 at this craft fair, her business will be successful enough for her to branch out to other craft fairs. How many ornaments does she have to sell to earn a $40.00 profit? Write and solve an equation; then explain how the steps and operations used in your algebraic solution compare to an arithmetic solution.
Answer:
3.50x – 30 = 40
3.50x – 30 + 30 = 40 + 30
3.50x + 0 = 70
3.50x = 70
3.50x (\(\frac{1}{3.50}\))= 70(\(\frac{1}{3.50}\))
1x = 20
To find the answer arithmetically, I would have to combine the $40 profit and $30 rental fee, then divide that sum ($70) by the $3.50 that she earns per ornament after costs.
Kay must sell 20 ornaments.
Question 3.
Travis received a letter from his bank saying that his checking account balance fell below zero. His account transaction log is shown below.
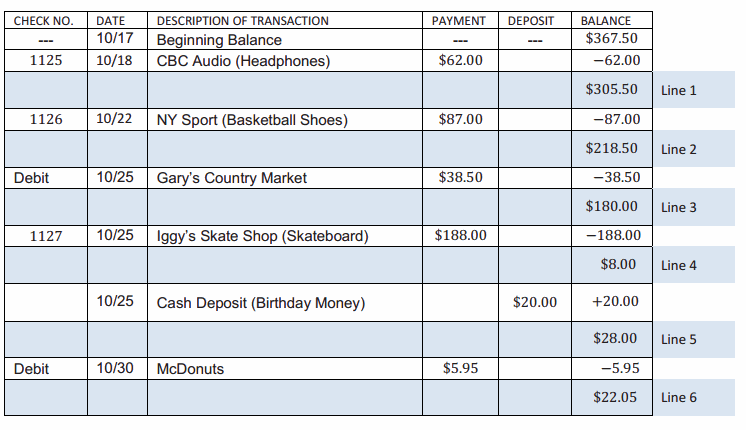
a. On which line did Travis make a mathematical error? Explain Travis’s mistake.
Answer:
On line 4, Travis subtracted $188 from $180 and got a positive answer. The difference should be -$8.00.
b. The bank charged Travis a $20 fee because his balance dropped below 0. He knows that he currently has an outstanding charge for $7.85 that he has not recorded yet. How much money will Travis have to deposit into his account so that the outstanding charge does not create another bank fee? Explain.
Answer:
Starting at Line 3:
180.00 – 188.00 + 20.00 – 5.95
-8.00 + 20.00 – 5.95
12.00 – 5.95
6.05
Travis’s actual balance should be $6.05.
6.05 + (- 20.00) overdraft fee
|-20.00| – | 6.05 |
– 13.95
– 13.95 + (-7.85) outstanding charge
| -13.95 | + | -7.85 |
– 21.80
To get his account back to 0, Travis needs to deposit $21.80 or more to avoid another overdraft fee.
Question 4.
The length of a rectangular envelope is 2\(\frac{1}{2}\) times its width. A plastic band surrounds the front and back of the envelope to secure it as shown in the picture. The plastic band is 39\(\frac{3}{8}\) inches long. Find the length and width of the envelope.
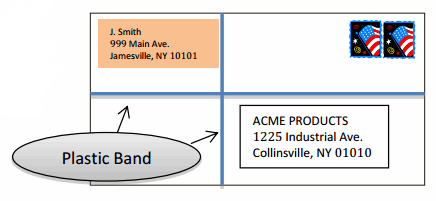
Answer:
The length of the plastic band is equivalent to the perimeter of the envelope.
Width: w
Length = 2\(\frac{1}{2}\) × width
w + w + (2\(\frac{1}{2}\)w) + (2\(\frac{1}{2}\)w) = 39\(\frac{3}{8}\)
2w + 5w = 39\(\frac{3}{8}\)
7w = 39\(\frac{3}{8}\)
7w = \(\frac{315}{8}\)
(\(\frac{1}{7}\))(7w) = (\(\frac{315}{8}\))(\(\frac{1}{7}\))
w = \(\frac{45}{8}\) = 5\(\frac{5}{8}\)
Length = 2\(\frac{1}{2}\) w
Length = 2\(\frac{1}{2}\) (5\(\frac{5}{8}\))
Length =\(\frac{5}{2}\) × \(\frac{45}{8}\)
Length = \(\frac{225}{16}\) = 14\(\frac{1}{16}\)
The length of the envelope is 14\(\frac{1}{16}\) inches and the width is 5\(\frac{5}{8}\) inches.
Question 5.
Juan and Mary are playing the Integer Card Game. The cards in their hands are shown below:
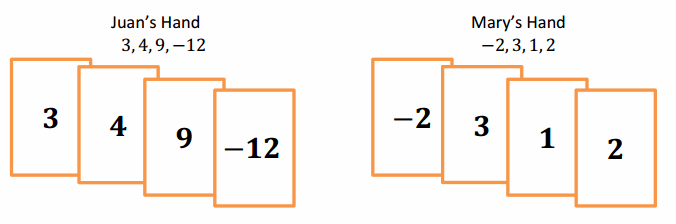
a. What are the scores in each of their hands?
Juan’s Score: 4
3 + 4 + 9 + (-12)
7 + 9 +(-12)
16 + (-12)
4
Mary’s Score: 4
-2 + 3 + 1 + 2
1 + 1 + 2
4
b. Lydia says that if Juan and Mary both take away their 3’s, Juan’s score will be higher than Mary’s. Marcus argues and says that Juan and Mary’s scores will be equal. Are either of them right? Explain.
Answer:
If both Juan and Mary lay down their 3’s, then both of their totals will be decreased by 3. Since both of their totals are 4, laying down a 3 would make both scores 1. Juan’s score and Mary’s score would be equal, so Marcus is correct.
c. Juan picks up another set of cards that is exactly like each card in his hand. Which of the following would make Mary’s score equal to Juan’s? Place a check mark ✓ by all that apply.
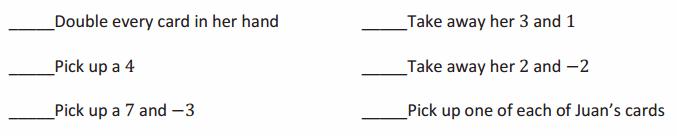
Explain why your selections will make Juan and Mary’s scores equal.
Answer:

Juan’s total doubles because every card in his hand doubled, so his total is 8. Each choice I selected would add 4 to Mary’s total to make it 8.