Engage NY Eureka Math 7th Grade Module 1 Lesson 3 Answer Key
Eureka Math Grade 7 Module 1 Lesson 3 Example Answer Key
Example
You have been hired by your neighbors to babysit their children on Friday night. You are paid $8 per hour. Complete the table relating your pay to the number of hours you worked.
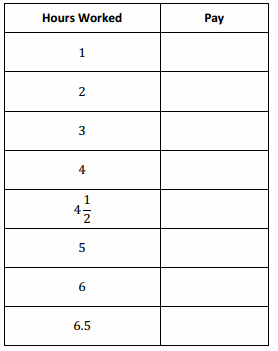
Answer:

Based on the table above, is the pay proportional to the hours worked? How do you know?
Answer:
Yes, the pay is proportional to the hours worked because every ratio of the amount of pay to the number of hours worked is the same. The
ratio is 8:1, and every measure of hours worked multiplied by 8 will result in the corresponding measure of pay.
![]()
Eureka Math Grade 7 Module 1 Lesson 3 Exercise Answer Key
For Exercises 1–3, determine if y is proportional to x. Justify your answer.
Question 1.
The table below represents the relationship of the amount of snowfall (in inches) in 5 counties to the amount of time (in hours) of a recent winter storm.
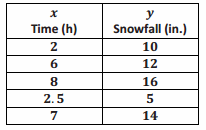
Answer:

y (snowfall) is not proportional to x (time) because all of the values of the ratios comparing snowfall to time are not equivalent. All of the values of the ratios must be the same for the relationships to be proportional. There is NOT one number such that each measure of x (time) multiplied by the number gives the corresponding measure of y (snowfall).
Question 2.
The table below shows the relationship between the cost of renting a movie (in dollars) to the number of days the movie is rented.
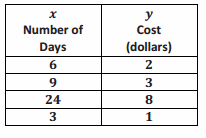
Answer:
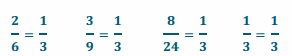
y (cost) is proportional to x (number of days) because all of the values of the ratios comparing cost to days are equivalent. All of the values of the ratios are equal to \(\frac{1}{3}\). Therefore, every measure of x (days) can be multiplied by the number \(\frac{1}{3}\) to get each corresponding measure of y (cost).
Question 3.
The table below shows the relationship between the amount of candy bought (in pounds) and the total cost of the candy (in dollars).
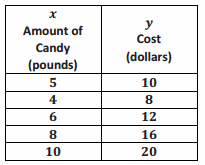
Answer:
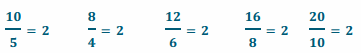
y(cost) is proportional to 𝐠(amount of candy) because all of the values of the ratios comparing cost to pounds are equivalent. All of the values of the ratios are equal to 𝟐 Therefore, every measure of x (amount of candy) can be multiplied by the number 2 to get each corresponding measure of y (cost).
Possible questions asked by the teacher or students:
→When looking at ratios that describe two quantities that are proportional in the same order, do the ratios always have to be equivalent?
→ Yes, all the ratios are equivalent, and a constant exists that can be multiplied by the measure of the first quantity to get the measure of the second quantity for every ratio pair.
→ For each example, if the quantities in the table were graphed, would the point (0,0) be on that graph? Describe what the point (0,0) would represent in each table.
→ Exercise 1: 0 inches of snowfall in 0 hours
→ Exercise 2: Renting a movie for 0 days costs $0
→ Exercise 3: 0 pounds of candy costs $0
→ Do the x- and y-values need to go up at a constant rate? In other words, when the x- and y-values both go up at a constant rate, does this always indicate that the relationship is proportional?
→ Yes, the relationship is proportional if a constant exists such that each measure of the x when multiplied by the constant gives the corresponding y-value.
Question 4.
Randy is driving from New Jersey to Florida. Every time Randy stops for gas, he records the distance he traveled in miles and the total number of gallons he used.
Assume that the number of miles driven is proportional to the number of gallons consumed in order to complete the table.

Answer:

Since the quantities are proportional, then every ratio comparing miles driven to gallons consumed must be equal. Using the given values for each quantity, the value of the ratio is
\(\frac{54}{2}\) = 27 \(\frac{216}{8}\)=27
If the number of gallons consumed is given and the number of miles driven is the unknown, then multiply the number of gallons consumed by 27 to determine the number of miles driven.
4(27)=108 10(27)=270 12(27)=324
If the number of miles driven is given and the number of gallons consumed is the unknown, then divide the number of miles driven by 27
to determine the number of gallons consumed.
\(\frac{189}{27}\) = 7
→ Why is it important for you to know that the number of miles are proportional to the number of gallons used?
→Without knowing this proportional relationship exists, just knowing how many gallons you consumed will not allow you to determine how many miles you traveled. You would not know if the same relationship exists for each pair of numbers.
→Describe the approach you used to complete the table.
→ Since the number of miles driven is proportional to the number of gallons consumed, a constant exists such that every measure of gallons used can be multiplied by the constant to give the corresponding amount of miles driven. Once this constant is found to be 27, it can be used to fill in the missing parts by multiplying each number of gallons by 27.
→ What is the value of the constant? Explain how the constant was determined.
→ The value of the constant is 27. This was determined by dividing the given number of miles driven by the given number of gallons consumed.
→ Explain how to use multiplication and division to complete the table.
→ If the number of gallons consumed was given, then that number is to be multiplied by the constant of 27 to determine the amount of the miles driven. If the number of miles driven were given, then that number needs to be divided by the constant of 27 to determine the number of gallons consumed.
Eureka Math Grade 7 Module 1 Lesson 3 Exit Ticket Answer Key
The table below shows the price, in dollars, for the number of roses indicated.

Question 1.
Is the price proportional to the number of roses? How do you know?
Answer:
The quantities are proportional to one another because there is a constant of 3 such that when the number of roses is multiplied by the constant, the result is the corresponding price.
Question 2.
Find the cost of purchasing 30 roses.
Answer:
If there are 30 roses, then the cost would be 30×3=$90.
Eureka Math Grade 7 Module 1 Lesson 3 Problem Set Answer Key
In each table, determine if y is proportional to x. Explain why or why not.
Question 1.
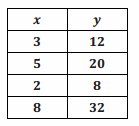
Yes, y is proportional to x because the values of all ratios of \(\frac{y}{x}\) are equivalent to 4. Each measure of x multiplied by this constant of 4 gives the corresponding measure in y.
Question 2.

Answer:
No, y is not proportional to x because the values of all the ratios of \(\frac{y}{x}\) are not equivalent. There is not a constant where every measure of x multiplied by the constant gives the corresponding measure in y. The values of the ratios are 5, 4.25, 3.8, and 3.5.
Question 3.

Answer:
Yes, y is proportional to x because a constant value of \(\frac{2}{3}\) exists where each measure of x multiplied by this constant gives the corresponding measure in y.
Question 4.
Kayla made observations about the selling price of a new brand of coffee that sold in three different-sized bags. She recorded those observations in the following table:
| Ounces of Coffee | |||
| Price in Dollars |
a. Is the price proportional to the amount of coffee? Why or why not?
Answer:
Yes, the price is proportional to the amount of coffee because a constant value of 0.35 exists where each measure of x multiplied by this constant gives the corresponding measure in y.
b. Use the relationship to predict the cost of a 20 oz. bag of coffee.
Answer:
20 ounces will cost $7.
Question 5.
you and your friends go to the movies. The cost of admission is $9.50 per person. Create a table showing the relationship between the number of people going to the movies and the total cost of admission. Explain why the cost of admission is proportional to the amount of people.
Answer:
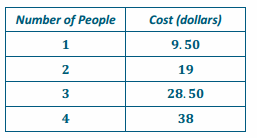
The cost is proportional to the number of people because a constant value of 9.50 exists where each measure of the number of people multiplied by this constant gives the corresponding measure in y.
Question 6.
For every 5 pages Gil can read, his daughter can read 3 pages. Let g represent the number of pages Gil reads, and let d represent the number of pages his daughter reads. Create a table showing the relationship between the number of pages Gil reads and the number of pages his daughter reads.
Is the number of pages Gil’s daughter reads proportional to the number of pages he reads? Explain why or why not.
Answer:
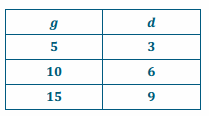
Yes, the number of pages Gil’s daughter reads is proportional to the number of pages Gil reads because all the values of the ratios are equivalent to 0.6. When I divide the number of pages Gil’s daughter reads by the number of pages Gil reads, I always get the same quotient. Therefore, every measure of the number of pages Gil reads multiplied by the constant 0.6 gives the corresponding values of the number of pages Gil’s daughter’s reads.
Question 7.
The table shows the relationship between the number of parents in a household and the number of children in the same household. Is the number of children proportional to the number of parents in the household? Explain why or why not.
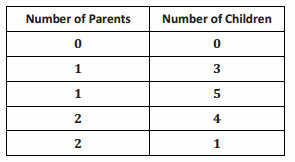
Answer:
No, there is not a proportional relationship because there is no constant such that every measure of the number of parents multiplied by the constant would result in the corresponding values of the number of children. When I divide the number of children by the corresponding number of parents, I do not get the same quotient every time. Therefore, the values of the ratios of children to parents are not equivalent. They are 3, 5, 2, and 0.5.
Question 8.
The table below shows the relationship between the number of cars sold and the amount of money earned by the car salesperson. Is the amount of money earned, in dollars, proportional to the number of cars sold? Explain why or why not.
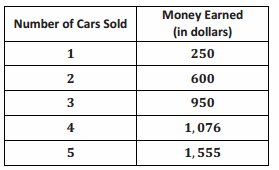
Answer:
No, there is no constant such that every measure of the number of cars sold multiplied by the constant would result in the corresponding values of the earnings because the ratios of money earned to number of cars sold are not equivalent; the values of the ratios are 250, 300, 316\(\frac{2}{3}\), 269, and 311.
Question 9.
Make your own example of a relationship between two quantities that is NOT proportional. Describe the situation, and create a table to model it. Explain why one quantity is not proportional to the other
Answer:
Answers will vary but should include pairs of numbers that do not always have the same value \(\frac{B}{A}\).