Engage NY Eureka Math 7th Grade Module 1 Lesson 2 Answer Key
Eureka Math Grade 7 Module 1 Lesson 2 Example Answer Key
Example 1.
Pay by the Ounce Frozen Yogurt
The purpose of this example is for students to understand when measures of one quantity are proportional to measures of another quantity.
Answer:
A new self-serve frozen yogurt store opened this summer that sells its yogurt at a price based upon the total weight of the yogurt and its toppings in a dish. Each member of Isabelle’s family weighed his dish, and this is what they found. Determine if the cost is proportional to the weight.
| Weight (ounces) | ||||
| Cost ($) |
The cost _____________________________________ the weight.
Discuss the following questions:
→ Does everyone pay the same cost per ounce? How do you know?
→ Yes, it costs $0.40 per ounce. If we divide each cost value by its corresponding weight, it will give the same unit price (or unit rate) of 0.40. Since we want to compare cost per ounce, we can use the unit (cost per ounce) to determine that we want to divide each cost value by each corresponding weight value.
→ Isabelle’s brother takes an extra-long time to create his dish. When he puts it on the scale, it weighs
15 ounces. If everyone pays the same rate in this store, how much will his dish cost? How did you calculate this cost?
→ $6. I determined the cost by multiplying 0.40 by 15 ounces.
→ Since this is true, we say “the cost is proportional to the weight.” Complete the statement in your materials.
→What happens if you don’t serve yourself any yogurt or toppings? How much do you pay?
→ $0.
→ Does the relationship above still hold true? In other words, if you buy 0 ounces of yogurt, then multiply by the cost per ounce, do you get 0?
→ Even for 0, you can still multiply by this constant value to get the cost (not that you would do this, but we can examine this situation for the sake of developing a rule that is always true).
→ Always multiply the number of ounces, x, by the constant that represents cost per ounce to get the total cost, y. Pause with students to note that any variables could be chosen but that for the sake of this discussion, they are x and y.
The teacher should label the table with the indicated variables and guide students to do the same.
→ For any measure x, how do we find y?
→ Multiply it by 0.40 (unit price).
→ Indicate this on the given chart, as done below. Be sure students do the same.

→ So, y = 0.40x.
Example 2.
A Cooking Cheat Sheet
In the back of a recipe book, a diagram provides easy conversions to use while cooking.
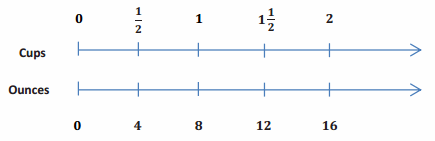
The ounces _____________________________________the cups.
Answer:
- What does the diagram tell us?
- The number of ounces in a given number of cups. More specifically, each pair of numbers indicates the correct matching of ounces to cups.
- Is the number of ounces proportional to the number of cups? How do you know?
- Yes, you can multiply each number of cups by 8 to get the number of ounces.
Have students complete the statement on their materials, ounces is proportional to cups, and note how they can tell. It is important to acknowledge that they could also divide by 8 if they know the number of ounces and are trying to find the number of cups. This discussion should lead to the importance of defining the quantities clearly.
- How many ounces are there in 4 cups? 5 cups? 8 cups? How do you know?
- 32, 40, 64; each time, the number of cups is multiplied by 8 to get the number of ounces.
- For the sake of this discussion (and to provide continuity between examples), let’s represent the cups with x, and the ounces with y.
The teacher should label the diagram with the indicated variables and guide students to do the same.
- For any number of cups x, how do we find the number of ounces, y?
- Multiply x by 8.
- So, y=8x.
- If we want to verify that our equation is y=8x, which x and y values can we use to see if it is true? How do you know?
- We can choose any pair of given (x,y) values since the equation should model the relationship for every pair of values.
It is a good idea to check more than one pair. Guide students to substitute the pairs of values into the equation to prove that for each one, the equation is true.
Example 3:
Summer Job
Alex spent the summer helping out at his family’s business. He was hoping to earn enough money to buy a new $220 gaming system by the end of the summer. Halfway through the summer, after working for 4 weeks, he had earned $112. Alex wonders, “If I continue to work and earn money at this rate, will I have enough money to buy the gaming system by the end of the summer?”
To determine if he will earn enough money, he decided to make a table. He entered his total money earned at the end of Week 1 and his total money earned at the end of Week 4.

a. Work with a partner to answer Alex’s question.
Answer:
Yes, Alex will have earned enough money to buy the $220 gaming system by the end of the summer because he will have earned 8∙28, or 224 dollars, for the 8 weeks he worked. A sample table is shown below.

Allow for students to share responses with the class for part (b), and then record in their student pages.
b. Are Alex’s total earnings proportional to the number of weeks he worked? How do you know?
Answer:
Alex’s total earnings are proportional to the number of weeks he worked. There exists a constant value, 28, which can be multiplied by the number of weeks to determine the corresponding earnings for that week. The table shows an example of a proportional relationship.
Eureka Math Grade 7 Module 1 Lesson 2 Exercise Answer Key
Exercise 1.
Have students complete the following example independently, and then discuss responses as a class.
During Jose’s physical education class today, students visited activity stations. Next to each station was a chart depicting how many calories (on average) would be burned by completing the activity.
Calories Burned While Jumping Rope

a. Is the number of calories burned proportional to time? How do you know?
Answer:
Yes, the time is always multiplied by the same number, 11, to find the calories burned.
b. If Jose jumped rope for 6.5 minutes, how many calories would he expect to burn?
Answer:
Jose would expect to burn 71.5 calories since 6.5 times 11 is 71.5.
Eureka Math Grade 7 Module 1 Lesson 2 Exit Ticket Answer Key
Ms. Albero decided to make juice to serve along with the pizza at the Student Government party. The directions said to mix 2 scoops of powdered drink mix with a half gallon of water to make each pitcher of juice. One of Ms. Albero’s students said she will mix 8 scoops with 2 gallons of water to make 4 pitchers. How can you use the concept of proportional relationships to decide whether the student is correct?
Answer:

As long as the amount of water is proportional to the number of scoops of drink mix, then the second quantity, amount of water, can be determined by multiplying the first quantity by the same constant. In this case, if the amount of powdered drink mix is represented by x, and the gallons of water are represented by y, then y = \(\frac{1}{4}\) x. To determine any of the measures of water, you will multiply the number of scoops by \(\frac{1}{4}\).
Eureka Math Grade 7 Module 1 Lesson 2 Problem Set Answer Key
Question 1.
A cran-apple juice blend is mixed in a ratio of cranberry to apple of 3 to 5.
a. Complete the table to show different amounts that are proportional.

Answer:

b. Why are these quantities proportional?
Answer:
The amount of apple is proportional to the amount of cranberry since there exists a constant number, \(\frac{5}{3}\), that when multiplied by any of the given measures for the amount of cranberry always produces the corresponding amount of apple. If the amount of cranberry is represented by x, and the amount of apple is represented by y, then each pair of quantities satisfies the equation y = \(\frac{5}{3}\)x. A similar true relationship could be derived by comparing the amount of cranberry to the amount of apple. In the case where x is the amount of apple and y is the amount of cranberry, the equation would be y = \(\frac{3}{5}\)x.
Question 3
John is filling a bathtub that is 18 inches deep. He notices that it takes two minutes to fill the tub with three inches of water. He estimates it will take 10 more minutes for the water to reach the top of the tub if it continues at the same rate. Is he correct? Explain.
| Time (minutes) | |||
| Bathtub Water Height (inches) |
Answer:
Yes. In 10 more minutes, the tub will reach 18 inches. At that time, the ratio of time to height may be expressed as 12 to 18, which is equivalent to 2 to 3. The height of the water in the bathtub increases 1\(\frac{1}{2}\) inches every minute.
