Engage NY Eureka Math Grade 6 Module 6 Lesson 19 Answer Key
Eureka Math Grade 6 Module 6 Lesson 19 Exercise Answer Key
There was also a 15-kilometer race. The ages of the 55 participants in that race appear below.
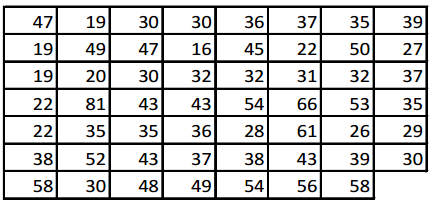
Does the longer race appear to attract different runners in terms of age? Below are side-by-side box plots that may help answer that question. Side-by-side box plots are two or more box plots drawn using the same scale. What do you notice about the two box plots?
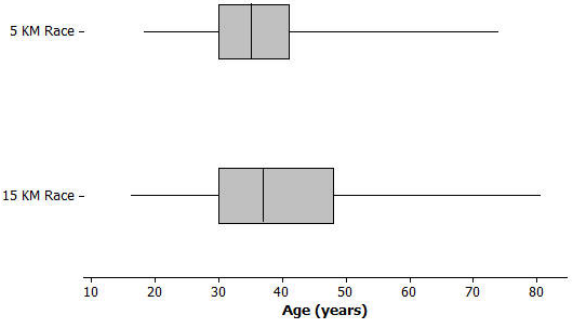
Both the range and the IQR are larger for the longer race, which means there is more variability in the ages for the long race than in the ages for the short race.
Exercises 1 – 6:
Exercise 1.
Based on the box plots, estimate the values in the five-number summary for the ages in the 15-kilometer race data set.
Answer:
Minimum – 16, Q1 = 30, Median = 37, Q3 = 48, ond Maximum = 81.
Exercise 2.
Do the two data sets have the same median? If not, which race had the higher median age?
Answer:
The two data sets do not have the same median; the 15 km race has a slightly higher median: 37 years of age compared to 35 years of age for the 5 km race.
Exercise 3.
Do the two data sets have the same IQR? If not, which distribution has the greater spread in the middle 50% of its distribution?
Answer:
The two data sets do not have the same IQR; the 15 km race has a slightly higher IQR: 18 years of age compared to 11 years of age for the 5 km race. The ages of runners in the middle 50% for the 15 km race are more spread out.
Exercise 4.
Which race had the smaller overall range of ages? What do you think the range of ages is for the 15-kilometer race?
Answer:
The 5 km race hod the smaller range of ages: 56 compared to 65 for the 15 km race.
Exercise 5.
Which race had the oldest runner? About how old was this runner?
Answer:
The 15 km race had the oldest runner at 81 years of age. The oldest runner for the 5 km race was only 74.
Exercise 6.
Now, consider just the youngest 25% of the runners in the 15-kilometer race. How old was the youngest runner in this group? How old was the oldest runner in this group? How does that compare with the 5-kilometer race?
Answer:
For the 15 km race, the youngest 25% of the runners had ages between the minimum and Q1. The youngest runner was 16 years old because this was the minimum for this distribution. The oldest runner in this group was 30 years old or younger because Q1 was 30. For the 5 km race, this youngest runner was 18 years old, and the oldest runner in the bottom 25% was 30 years old or younger (both distributions have the same Q1).
Exercises 7 – 12: Comparing Box Plots
In 2012, Major League Baseball had two leagues: an American League of 14 teams and a National League of 16 teams. Jesse wondered if American League teams have higher batting averages and on-base percentages. (Higher values are better.) Use the following box plots to investigate.
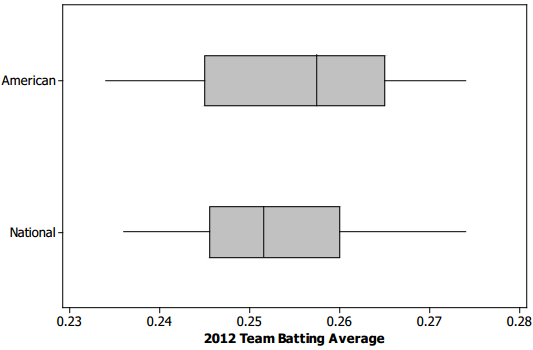
Exercise 7.
Was the highest American League team batting average very different from the highest National League team batting average? Approximately how large was the difference, and which league had the higher maximum value?
Answer:
The highest batting averages for both leagues appear to be around 0.274. (This value must be estimated from the box plot; so other answers that are dose to 0.274 are acceptable.)
Exercise 8.
Was the range of the American League team batting averages very different or only slightly different from the range of the National League team batting averages?
Answer:
They appear to be only slightly different, with the American League range being slightly higher. The American League minimum (0.234) is slightly lower than the National League minimum (0,236), and both leagues appear to have the same maximum.
Exercise 9.
Which league had the higher median team batting average? Given the scale of the graph and the range of the data sets, does the difference between the median values for the two leagues seem to be small or large? Explain why you think it is small or large.
Answer:
The American League has a higher median batting average of about 0.258, while the median batting average for the National League median is about 0.252. In answering the second part of this question, make sure that students look at the difference in the medians. Students might say that they think this is a small difference because 0.006 is a small number.
However, a better answer would consider the scale and the range of the data. The difference of 0.006 is roughly \(\frac{1}{6}\) of the range for the National League, which suggests that the difference may be large enough to be considered meaningful.
Exercise 10.
Based on the box plots below for on-base percentage, which three summary values (from the five-number summary) appear to be the same or virtually the same for both leagues?
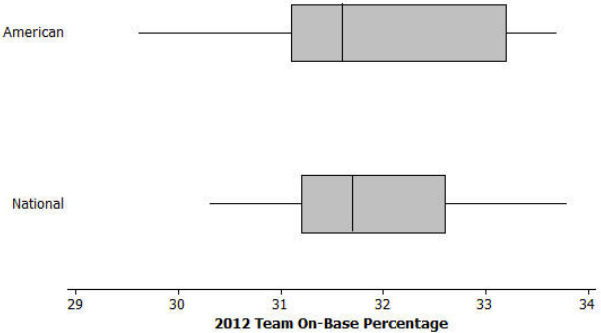
Answer:
The Q1, median, and maximum appear to be roughly the same.
Exercise 11.
Which league’s data set appears to have less variability? Explain.
Answer:
The National League data set appears to have less variability, as it has a smaller IQR and smaller range.
Exercise 12.
Recall that Jesse wondered if American League teams have higher batting averages and on-base percentages. Based on the box plots given above, what would you tell Jesse?
Answer:
Answers will vary.
It does look like the American League teams tend to have higher team batting averages. The median and upper quartile for the American League team batting average box plot are greater than the median and upper quartile for the National League.
However, there is at least one team in the American League with a team batting average that is lower than every team in the National League, and there is at least one team in the National League that has a team batting average that is about the same as the American League team with the highest batting average.
For on-base percentage, the median and lower quartile and the maximum are about the same for both leagues. So it does not really look like it would be reasonable to say that the American League teams tend to have higher team on-base percentages than National League teams.
Eureka Math Grade 6 Module 6 Lesson 19 Problem Set Answer Key
Question 1.
College athletic programs are separated into divisions based on school size, available athletic scholarships, and other factors. A researcher wondered if members of swimming and diving programs in Division I (usually large schools that offer athletic scholarships) tend to be taller than the swimmers and divers in Division III programs (usually smaller schools that do not offer athletic scholarships).
To begin the investigation, the researcher creates side-by side box plots for the heights (in inches) of 41 male swimmers and divers at Mountain Vista University (a Division I program) and the heights (in inches) of 10 male swimmers and divers at Eaglecrest College (a Division III program).
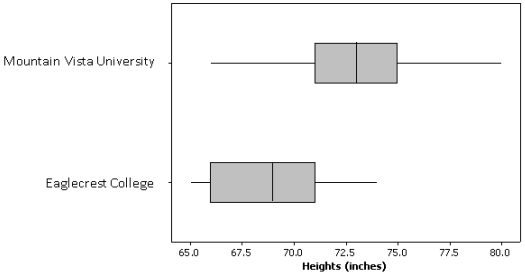
a. Which data set has the smaller range?
Answer:
Eaglecrest College has a smaller range.
b. True or false: A swimmer who had a height equal to the median for the Mountain Vista University would be taller than the median height of swimmers and divers at Eaglecrest College.
Answer:
True
c. To be thorough, the researcher will examine many other colleges’ sports programs to further investigate the claim that members of swimming and diving programs in Division I are generally taller than the swimmers and divers in Division III. But given the graph above, in this initial stage of her research, do you think that the claim might be valid? Carefully support your answer using summary measures or graphical attributes.
Answer:
Based on just these two teams, it looks like the claim may be correct. A large portion of the Mountain Vista University distribution is higher than the maximum value of the Eaglecrest College distribution. The median value for the Mountain Vista University appears to be 4 inches higher than the median value of the Eogkcrest College distribution.
Question 2.
Data on the weights (in pounds) of 100 polar bears and 50 grizzly bears are summarized in the box plots shown below.
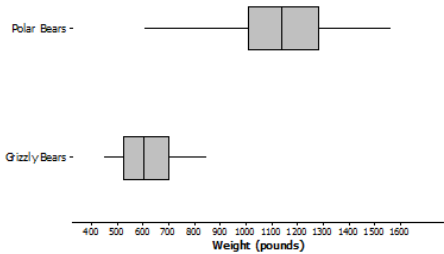
a. True or false: At least one of the polar bears weighed more than the heaviest grizzly bear. Explain how you know.
Answer:
True. The lower quartile and the median weight for the polar bears were greater than the maximum weight for the grizzly bears, so at least 75% of the polar bears weighed more than the heaviest grizzly bear.
b. True or false: Weight differs more from bear to bear for polar bears than for grizzly bears. Explain how you know.
Answer:
True. The weights of the grizzly bears are more compact than the weights of the polar bears. The grizzly bear weight distribution has a smaller range and IQR than the polar bear weight distribution.
c. Which type of bear tends to weigh more? Explain.
Answer:
Polar bears tend to have greater weights. The median weight for grizzly bears is much smaller than the median polar bear weight, and about half of the grizzly bear weight distribution is lower than the minimum weight for the polar bears.
Question 3.
Many movie studios rely heavily on viewer data to determine how a movie will be marketed and distributed. Recently, previews of a soon-to-be-released movie were shown to 300 people. Each person was asked to rate the movie on a scale of 0 to 10, with 10 representing “best movie I have ever seen” and O representing “worst movie I have ever seen.”
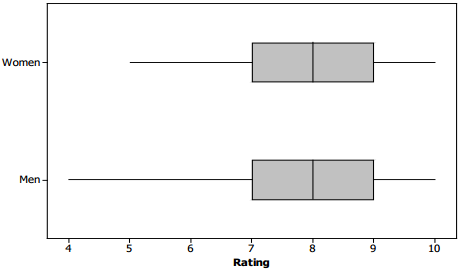
Below are some side-by-side box plots that summarize the ratings by gender and by age.
For 150 women and 150 men:
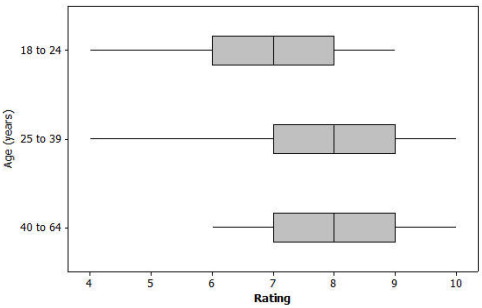
For 3 age groups:
a. Does it appear that the men and women rated the film in a similar manner or in a very different manner? Write a few sentences explaining your answer using comparative information about center and variability.
Answer:
It appears that the men and women rated the film in a very similar manner: The box plots show the same quartile values, the same medians, and the same maximums. The only difference is that the minimum rating from a man was slightly lower than the minimum rating from a woman.
b. It appears that the film tended to receive better ratings from the older members of the group. Write a few sentences using comparative measures of center and spread or aspects of the graphical displays to justify this claim.
Answer:
For the two oldest age groups, the Q1. median, Q3, and maximum values are all higher than the 18 – 24 counterparts. In fact, the Q1 value for each of these two older groups equals the median rating of the youngest group, and the median value for each of these two older groups equals the Q3 rating of the youngest group.
Additionally, while the two oldest groups have similar distributions, the minimum score of the oldest group was much higher than the minimum value of the 25 – 39 group. This means that none of the 40 – 64 respondents rated the movie with a score as low as a 4 (as was the case in the 25 – 39 age group).
Eureka Math Grade 6 Module 6 Lesson 19 Exit Ticket Answer Key
Hay is used to feed animals such as cows, horses, and goats. Almost \(\frac{1}{3}\) of the hay grown in the United States comes from just five states. Is this because these states have more acres planted in hay, or could it be because these states produce more hay per acre than other states? The following box plots show the distribution of hay produced (in tons) per acre planted in hay for three different regions: 22 eastern states, 14 midwestern states, and 12 western states.
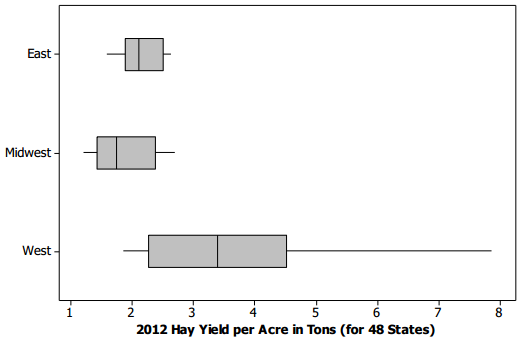
Question 1.
Which of the three regions’ data sets has the least variability? Which has the greatest variability? To explain how you chose your answers, write a sentence or two that supports your choices by comparing relevant summary measures (such as median and lOR) or aspects of the graphical displays (such as shape and variability).
Answer:
The East data set has the least variability, as it has the smallest range and the smallest IQR. The West data set has the greatest variability, as it has the largest range and the largest IQR.
Question 2.
True or false: The western state with the smallest hay yield per acre has a higher hay yield per acre than at least half of the midwestern states. Explain how you know this is true or how you know this is false.
Answer:
This is true; the minimum value of the West data set is higher than the median value of the Midwest data set. Therefore, this minimum value for the West must be higher than at least half of the midwestern states’ values.
Question 3.
Which region typically has states with the largest hay yield per acre? To explain how you chose your answer, write a sentence or two that supports your choice by comparing relevant summary measures or aspects of the graphical displays.
Answer:
The West typically has states with the largest hay yield per acre. Over half of the western states have hay yields that are higher than any yield in either of the other two regions Also, some western yields are more than two times the largest eastern and midwestern yields.