Engage NY Eureka Math 6th Grade Module 4 Lesson 7 Answer Key
Eureka Math Grade 6 Module 4 Lesson 7 Example Answer Key
Example 1.
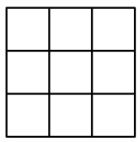
What is the length of one side of this square?
Answer:
3 units
What is the formula for the area of a square?
Answer:
A = s2
What is the square’s area as a multiplication expression?
Answer:
3 units × 3 units
What is the square’s area?
Answer:
9 square units
We can count the units. However, look at this other square. Its side length is 23 That is just too many tiny units to draw. What expression can we build to find this square’s area?
Answer:
23 × 23 cm
What is the area of the square? Use a calculator if you need to.
Answer:
529 cm2
Example 2.
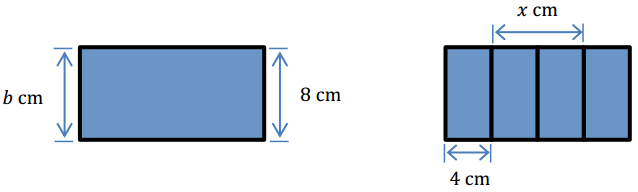
What does the letter represent in this blue rectangle?
Answer:
b = 8
With a partner, answer the following question: Given that the second rectangle is divided into four equal parts, what number does the x represent?
Answer:
x = 8
How did you arrive at this answer?
Answer:
We reasoned that each width of the 4 congruent rectangles must be the same. Two 4 lengths equals
What is the total length of the second rectangle? Tell a partner how you know.
Answer:
The length consists of 4 segments that each has a length of 4 cm. 4 × 4 cm = 16 cm.
If the two large rectangles have equal lengths and widths, find the area of each rectangle.
Answer:
8 cm × 16 cm = 128 cm2
Discuss with your partner how the formulas for the area of squares and rectangles can be used to evaluate area for a particular figure.
Answer:
Example 3.
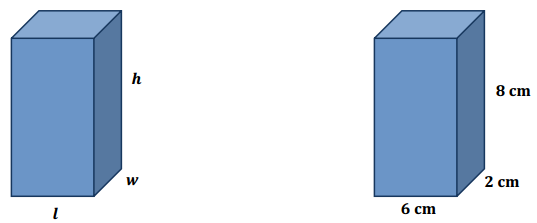
What does the l represent in the first diagram?
Answer:
The length of the rectangular prism
What does the w represent in the first diagram?
Answer:
The width of the rectangular prism
What does the h represent in the first diagram?
Answer:
The height of the rectangular prism
Since we know the formula to find the volume is V = l × w ×h, what number can we substitute for the l in the formula? Why?
Answer:
6, because the length of the second right rectangular prism is 6 cm.
What other number can we substitute for the l?
Answer:
No other number can replace the l. Only one number can replace one letter.
What number can we substitute for the in the formula? Why?
Answer:
2, because the width of the second right rectangular prism is 2 cm.
What number can we substitute for the h in the formula?
Answer:
8 because the height of the second right rectangular prism is 8 cm.
Determine the volume of the second right rectangular prism by replacing the letters in the formula with their appropriate numbers.
Answer:
V = l × w × h; V = 6 cm × 2 cm × 8 cm = 96 cm3
Eureka Math Grade 6 Module 4 Lesson 7 Exercise Answer Key
Exercise 1.
Complete the table below for both squares. Note: These drawings are not to scale.
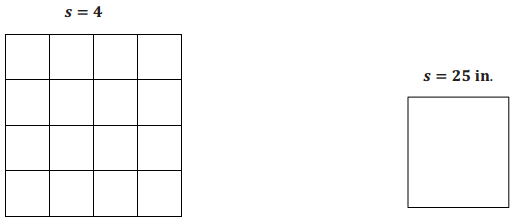

Answer:

Exercise 2.
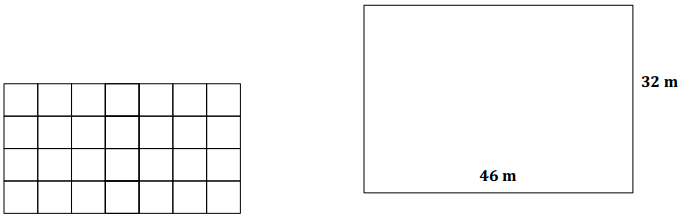

Answer:

Exercise 3.
Complete the table for both figures. Using a calculator is appropriate.
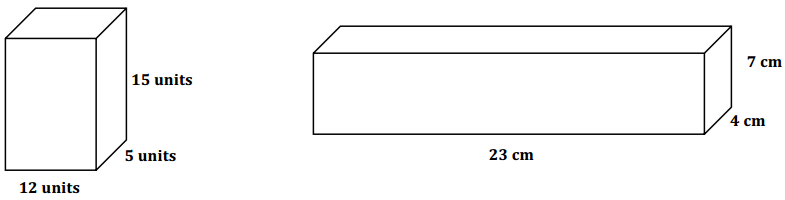
Answer:

Eureka Math Grade 6 Module 4 Lesson 7 Problem Set Answer Key
Question 1.
Replace the side length of this square with 4 in., and find the area.

Answer:
The student should draw a square, label the side 4 in., and calculate the area to be 16 in2.
Question 2.
Complete the table for each of the given figures.
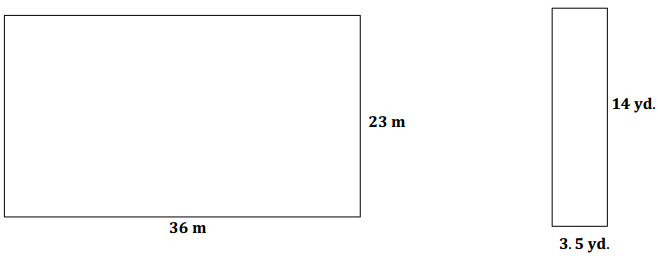

Answer:

Question 3.
Find the perimeter of each quadrilateral in Problems 1 and 2.
Answer:
p = 16 in. p = 118 p = 35 yd.
Question 4.
Using the formula V = l × w × h, find the volume of a right rectangular prism when the length of the prism is 45 cm, the width is 12 cm, and the height is 10 cm.
Answer:
V = l × w × h; V = 45 cm × 12 cm × 10 cm = 5,400 cm3
Eureka Math Grade 6 Module 4 Lesson 7 Exit Ticket Answer Key
Question 1.
In the drawing below, what do the letters and represent?
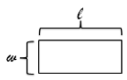
Answer:
Length and width of the rectangle
Question 2.
What does the expression l + w + l + w represent?
Answer:
Perimeter of the rectangle, or the sum of the sides of the rectangle
Question 3.
What does the expression l ∙ w represent?
Answer:
Area of the rectangle
Question 4.
The rectangle below is congruent to the rectangle shown in Problem 1. Use this information to evaluate the expressions from Problems 2 and 3.
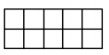
Answer:
l = 5 and w = 2 p = 14 units A = 10 units2