Engage NY Eureka Math 6th Grade Module 1 Lesson 17 Answer Key
Eureka Math Grade 6 Module 1 Lesson 17 Example Answer Key
Example 1
Write each ratio as a rate.
a. The ratio of miles to the number of hours is 434 to 7.
Answer:
Miles to hour: 434: 7
Student responses: \(\frac{434}{7} \frac{\text { miles }}{\text { hours }}\) = 62 miles/hour
b. The ratio of the number of laps to the number of minutes is 5 to 4.
Answer:
Laps to minute: 5:4
Student responses: \(\frac{5}{4} \frac{\text { laps }}{\text { minutes }}=\frac{5}{4}\) laps/mm
Example 2.
a. Complete the model below using the ratio from Example 1, part (b).
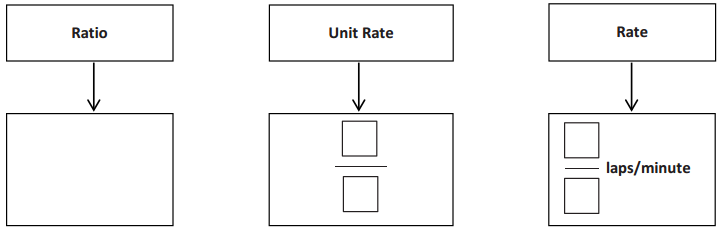
Answer:
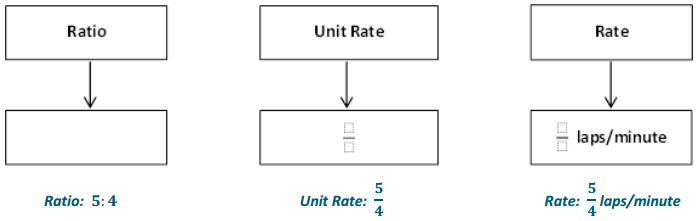
b. Complete the model below now using the rate listed below.
Answer:
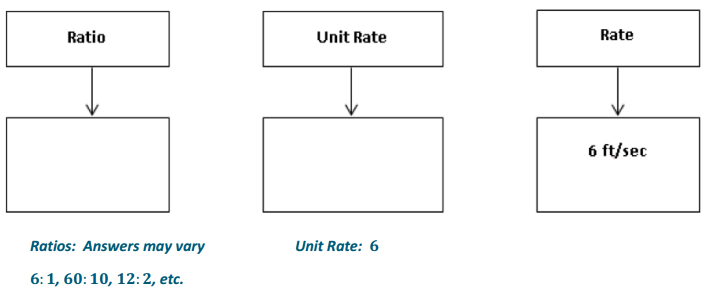
Examples 3.
Dave can clean pools at a constant rate of pools/hour.
a. What is the ratio of the number of pools to the number of hours?
Answer:
3: 5
b. How many pools can Dave clean in 10 hours?
Answer:
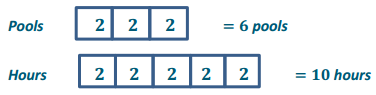
Dave can clean 6 pools in 10 hours.
c. How long does it take Dave to clean 15 pools?
Answer:
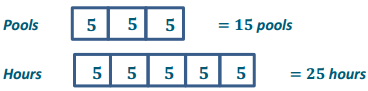
It will take Dave 25 hours to clean 15 pools.
Example 4.
Emeline can type at a constant rate of \(\frac{1}{4}\) pages/minute.
a. What is the ratio of the number of pages to the number of minutes?
Answer:
1: 4
b. Emeline has to type a 5-page article but only has 18 minutes until she reaches the deadline. Does Emeline have enough time to type the article? Why or why not?
Answer:
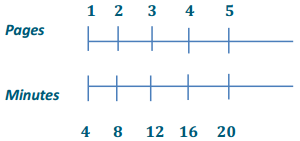
No, Emeline will not have enough time because It will take her 20 minutes to type a 5-page article.
c. Emeline has to type a 7-page article. How much time will It take her?
Answer:
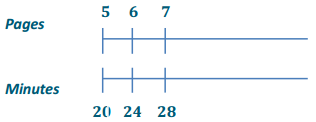
It will take Emeline 28 minutes to type a 7-page article.
Example 5.
Xavier can swim at a constant speed of \(\frac{5}{3}\) meters/second.
a. What is the ratio of the number of meters to the number of seconds?
Answer:
5: 3
b. Xavier is trying to qualify for the National Swim Meet. To qualify, he must complete a 100-meter race in 55 seconds. Will Xavier be able to qualify? Why or why not?
Answer:
| Meters | Seconds |
| 5 | 3 |
| 10 | 6 |
| 100 | 60 |
Xavier will not qualify for the meet because he would complete the race in 60 seconds.
c. Xavier is also attempting to qualify for the same meet in the 200-meter event. To qualify, Xavier would have to complete the race in 130 seconds. Will Xavier be able to qualify in this race? Why or why not?
Answer:
| Meters | Seconds |
| 100 | 60 |
| 200 | 120 |
Xavier will qualify for the meet in the 200 meter race because he would complete the race in 120 seconds.
Example 6.
The corner store sells apples at a rate of 1. 25 dollars per apple.
a. What is the ratio of the amount in dollars to the number of apples?
Answer:
1.25: 1
b. Akia is only able to spend $10 on apples. How many apples can she buy?
Answer:
8 apples
c. Christian has $6 in his wallet and wants to spend it on apples. How many apples can Christian buy?
Answer:
Christian can buy 4 apples and would spend $5. 00. Christian cannot buy 5 apples because it would cost $6.25, and he only has $6.00.
Eureka Math Grade 6 Module 1 Lesson 17 Problem Set Answer Key
Question 1.
Once a commercial plane reaches the desired altitude, the pilot often travels at a cruising speed. On average, the cruising speed is 570 miles/hour. If a plane travels at this cruising speed for 7 hours, how far does the plane travel while cruising at this speed?
Answer:
3,990 miles
Question 2.
Denver, Colorado often experiences snowstorms resulting in multiple inches of accumulated snow. During the last snow storm, the snow accumulated at \(\frac{4}{5}\) inch/hour. If the snow continues at this rate for 10 hours, how much snow will accumulate?
Answer:
8 inches
Eureka Math Grade 6 Module 1 Lesson 17 Exit Ticket Answer Key
Tiffany is filling her daughter’s pool with water from a hose. She can fill the pool at a rate of \(\frac{1}{10}\) gallons/second. Create at least three equivalent ratios that are associated with the rate. Use a double number line to show your work.
Answer:
Answers will vary.