Engage NY Eureka Math 6th Grade Module 1 Lesson 13 Answer Key
Eureka Math Grade 6 Module 1 Lesson 13 Exercise Answer Key
Exercise 1
Jorge is mixing a special shade of orange paint. He mixed 1 gallon of red paint with 3 gallons of yellow paint. Based on this ratio, which of the following statements are true?
→ \(\frac{3}{4}\) of a 4 gallon mix would be yellow paint.
Answer:
True
→ Every 1 gallon of yellow paint requires \(\frac{1}{3}\) gallon of red paint. .
Answer:
True
→ Every 1 gallon of red paint requires 3 gallons of yellow paint.
Answer:
True
→ There is 1 gallon of red paint in a 4-gallon mix of orange paint,
Answer:
True
→ There are 2 gallons of yellow paint in an 8-gallon mix of orange paint.
Answer:
False
Use the space below to determine If each statement is true or false.

Answer:
Allow students to discuss each question with a partner or group. When the class comes back together as a whole group, each group is responsible for explaining to the class one of the statements and whether the group feels the statement is true or false and why. (The first four statements are true while the fifth statement is false. To be made true, the fifth statement should read “There are 6 gallons of yellow paint in an 8 galIon mix of orange paint.”)
Exercise 2.
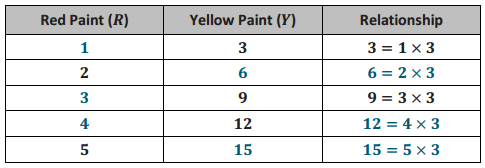
Based on the information on red and yellow paint given in Exercise 1, complete the table below.
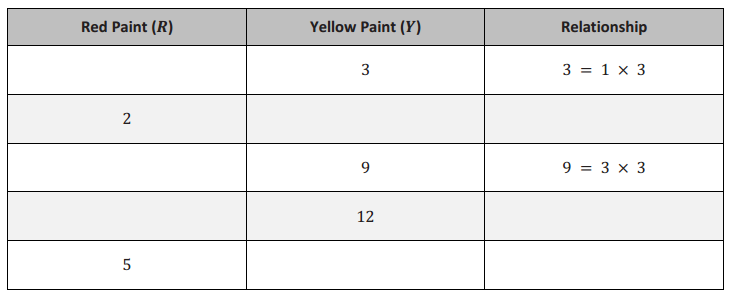
Answer:
Exercise 3
a. Jorge now plans to mix red paint and blue paint to create purple paint. The color of purple he has decided to make combines red paint and blue paint in the ratio 4: 1. If Jorge can only purchase paint in one gallon containers, construct a ratio table for all possible combinations for red and blue paint that will give Jorge no more than 25 gallons of purple paint.
Answer:

Write an equation that will let Jorge calculate the amount of red paint he will need for any given amount of blue paint.
Answer:
R = 4B
Write an equation that will let Jorge calculate the amount of blue paint he will need for any given amount o
red paint.
Answer:
B = \(\frac{1}{4}\)R
If Jorge has 24 gallons of red paint, how much blue paint will he have to use to create the desired color of purple?
Answer:
Jorge will have to use 6 gallons of blue paint.
If Jorge has 24 gallons of blue paint, how much red paint will he have to use to create the desired color of purple?
Answer:
Jorge will have to use 96 gallons of red paint.
b. Using the same relationship of red to blue from above, create a table that models the relationship of the three colors blue, red, and purple (total) paint. Let B represent the number of gallons of blue paint, let R represent the number of gallons of red paint, and let T represent the total number of gallons of (purple) paint. Then write an equation that models the relationship between the blue paint and the total amount of paint, and answer the questions.

Answer:
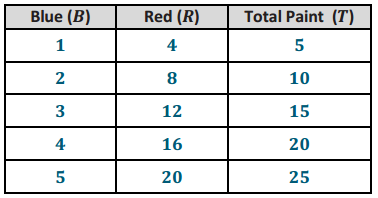
Equation:
Answer:
T = 5B
Value of the ratio of total paint to blue paint:
Answer:
\(\frac{5}{1}\)
How is the value of the ratio related to the equation?
Answer:
The value of the ratio is used to determine the total paint value by multiplying it with the blue paint value.
Exercise 4.
During a particular U.S. Air Force training exercise, the ratio of the number of men to the number of women was 6: 1. Use the ratio table provided below to create at least two equations that model the relationship between the number of men and the number of women participating in this training exercise.
Answer:
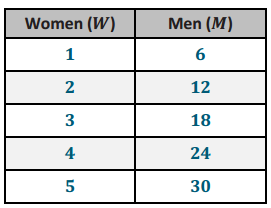
Equations:
Answer:
M = 6w
W = \(\left(\frac{1}{6}\right)\)M
\(\frac{M}{W}\) = 6
\(\frac{W}{M}\) = \(\frac{1}{6}\)
If 200 women participated in the training exercise, use one of your equations to calculate the number of men who participated.
Answer:
I can substitute 200 for the value of women and multiply by 6, the value of the ratio, to get the number of men. There would be 1,200 men participating in the training exercise.
Exercise 5.
Malia is on a road trip. During the first five minutes of Malia’s trip, she sees 18 cars and 6 trucks. Assuming this ratio of cars to trucks remains constant over the duration of the trip, complete the ratio table using this comparison. Let T represent the number of trucks she sees, and let C represent the number of cars she sees.
Answer:
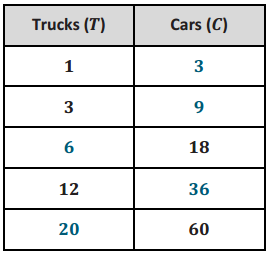
What is the value of the ratio of the number of cars to the number of trucks?
Answer:
\(\frac{3}{1}\)
What equation would model the relationship between cars and trucks?
Answer:
C = 3T and T = \(\left(\frac{1}{3}\right)\)C
At the end of the trip, Malla had counted 1, 254 trucks. How many cars did she see?
Answer:
C = 1,254.3; C = 3, 762 cars
Exercise 6
Kevin is training to run a half-marathon. His training program recommends that he run for 5 minutes and walk for 1 minute. Let R represent the number of minutes running, and let W represent the number of minutes walking.

Answer:

What is the value of the ratio of the number of minutes walking to the number of minutes running?
Answer:
\(\frac{1}{5}\)
What equation could you use to calculate the minutes spent walking if you know the minutes spent running?
Answer:
W = \(\frac{1}{5}\)R; Answers will vary.
Eureka Math Grade 6 Module 1 Lesson 13 Problem Set Answer Key
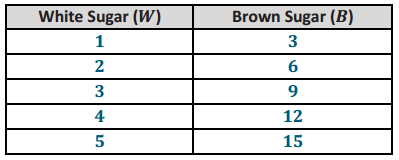
A cookie recipe calls for 1 cup of white sugar and 3 cups of brown sugar.
Make a table showing the comparison of the amount of white sugar to the amount of brown sugar.
Answer:
Question 1.
Write the value of the ratio of the amount of white sugar to the amount of brown sugar.
Answer:
\(\frac{1}{3}\)
Question 2.
Write an equation that shows the relationship of the amount of white sugar to the amount of brown sugar.
Answer:
B = 3W or W = \(\frac{1}{3}\) B
Question 3.
Explain how the value of the ratio can be seen In the table.
Answer:
The values in the first row show the values in the ratio. The ratio of the amount of brown sugar to the amount of white sugar is 3: 1. The value of the ratio is \(\frac{3}{1}\).
Question 4.
Explain how the value of the ratio can be seen in the equation.
Answer:
The amount of brown sugar is represented as B in the equation. The amount of white sugar is represented as W. The value is represented because the amount of brown sugar is three times as much as the amount of white sugar, or B = 3W.
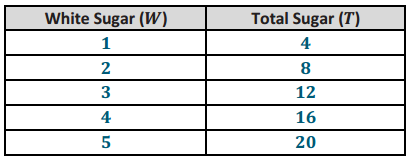
Using the same recipe, compare the amount of white sugar to the amount of total sugars used in the recipe.
Make a table showing the comparison of the amount of white sugar to the amount of total sugar.
Answer:
Question 5.
Write the value of the ratio of the amount of total sugar to the amount of white sugar.
Answer:
\(\frac{4}{1}\)
Question 6.
Write an equation that shows the relationship of total sugar to white sugar.
Answer:
T = 4W
Eureka Math Grade 6 Module 1 Lesson 13 Exit Ticket Answer Key
Question 1.
A carpenter uses four nails to install each shelf. Complete the table to represent the relationship between the number of nails (N) and the number of shelves (S). Write the ratio that describes the number of nails per number of shelves. Write as many different equations as you can that describe the relationship between the two quantities.
| Shelves (s) |
Nails (N) |
| 1 | 4 |
| 2 | |
| 12 | |
| 16 | |
| 5 |
Answer:
| Shelves (s) |
Nails (N) |
| 1 | 4 |
| 2 | 8 |
| 3 | 12 |
| 4 | 16 |
| 5 | 20 |
\(\left(\frac{N}{S}\right)=\left(\frac{4}{1}\right)\)
Equations:
N = 4s
S = \(\left(\frac{1}{4}\right)\)N