Engage NY Eureka Math 5th Grade Module 4 Lesson 25 Answer Key
Eureka Math Grade 5 Module 4 Lesson 25 Problem Set Answer Key
Question 1.
Draw a tape diagram and a number line to solve. You may draw the model that makes the most sense to you. Fill in the blanks that follow. Use the example to help you.
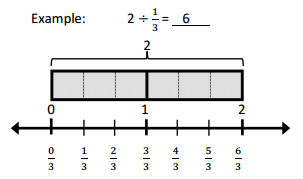
There are 3 halves in 1 whole.
There are 6 halves in 4 wholes.
If 2 is \(\frac{1}{3}\), what is the whole? 6
a. 4 ÷ \(\frac{1}{2}\) = _________
There are __ halves in 1 whole.
There are ___ halves in 4 wholes.
If 4 is \(\frac{1}{2}\), what is the whole? __
Answer:
4 ÷ \(\frac{1}{2}\) = 8
There are 2 halves in 1 whole.
There are 8 halves in 4 wholes.
If 4 is \(\frac{1}{2}\), the whole is 4.
Explanation:
Given that 4 ÷ \(\frac{1}{2}\) on solving we will get the result as 8. And there are 2 halves in 1 whole and there are 8 halves in 4 whole.
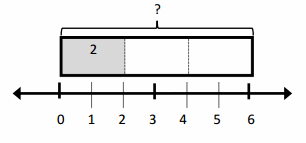
b. 2 ÷ \(\frac{1}{4}\) = __
There are ____ fourths in 1 whole.
There are ____ fourths in 2 wholes.
If 2 is \(\frac{1}{4}\), what is the whole? __
Answer:
2 ÷ \(\frac{1}{4}\) = 8
There are 4 fourths in 1 whole.
There are 8 fourths in 2 wholes.
If 2 is \(\frac{1}{4}\), the whole is 8
Explanation:
Given that 2 ÷ \(\frac{1}{4}\) on solving we will get the result as 8. And there are 4 fourths in 1 whole and there are 8 fourths in 2 wholes.
c. 5 \(\frac{1}{3}\) = __
There are ____ thirds in 1 whole.
There are ____ thirds in 5 wholes.
If 5 is \(\frac{1}{3}\), what is the whole? __
Answer:
5 \(\frac{1}{3}\) = 15
There are 3 thirds in 1 whole.
There are 15 thirds in 5 wholes.
If 5 is \(\frac{1}{3}\), the whole is 15.
Explanation:
Given that 5 \(\frac{1}{3}\) on solving we will get the result as 15. And there are 3 thirds in 1 whole and there are 15 thirds in 5 wholes.
d. 3 ÷ \(\frac{1}{5}\) = _________
There are ____ fifths in 1 whole.
There are ____ fifths in 3 wholes.
If 3 is \(\frac{1}{5}\), what is the whole? __
Answer:
3 ÷ \(\frac{1}{5}\) = 15
There are 5 fifths in 1 whole.
There are 15 fifths in 3 wholes.
If 3 is \(\frac{1}{5}\), the whole 15.
Explanation:
Given that 3 ÷ \(\frac{1}{5}\) on solving we will get the result as 15. And there are 5 fifths in 1 whole and tThere are 15 fifths in 3 wholes.
Question 3.
Divide. Then, multiply to check.
a. 5 ÷ \(\frac{1}{2}\)
Answer:
5 ÷ \(\frac{1}{2}\) = 10.
Explanation:
Given that 5 ÷ \(\frac{1}{2}\) which is 5 × 2 = 10. To check we will \(\frac{1}{2}\) × 10 which is 5.
b. 3 ÷ \(\frac{1}{2}\)
Answer:
3 ÷ \(\frac{1}{2}\) = 6.
Explanation:
Given that 3 ÷ \(\frac{1}{2}\) which is 3 × 2 = 6. To check we will \(\frac{1}{2}\) × 6 which is 3.
c. 4 ÷ \(\frac{1}{5}\)
Answer:
4 ÷ \(\frac{1}{5}\) = 20.
Explanation:
Given that 4 ÷ \(\frac{1}{5}\) which is 4 × 5 = 20. To check we will \(\frac{1}{5}\) × 20 which is 4.
d. 1 ÷ \(\frac{1}{6}\)
Answer:
1 ÷ \(\frac{1}{6}\) = 6.
Explanation:
Given that 1 ÷ \(\frac{1}{6}\) which is 1 × 6 = 6. To check we will \(\frac{1}{6}\) × 6 which is 1.
e. 2 ÷ \(\frac{1}{8}\)
Answer:
2 ÷ \(\frac{1}{8}\) = 16.
Explanation:
Given that 2 ÷ \(\frac{1}{8}\) which is 2 × 8 = 16. To check we will \(\frac{1}{8}\) × 16 which is 2.
f. 7 ÷ \(\frac{1}{6}\)
Answer:
7 ÷ \(\frac{1}{6}\) = 42.
Explanation:
Given that 7 ÷ \(\frac{1}{6}\) which is 7 × 6 = 42. To check we will \(\frac{1}{6}\) × 42 which is 7.
g. 8 ÷ \(\frac{1}{3}\)
Answer:
8 ÷ \(\frac{1}{3}\) = 24.
Explanation:
Given that 8 ÷ \(\frac{1}{3}\) which is 8 × 3 = 24. To check we will \(\frac{1}{3}\) × 24 which is 8.
h. 9 ÷ \(\frac{1}{4}\)
Answer:
9 ÷ \(\frac{1}{4}\) = 36.
Explanation:
Given that 9 ÷ \(\frac{1}{4}\) which is 9 × 4 = 36. To check we will \(\frac{1}{4}\) × 36 = 9.
Question 3.
For an art project, Mrs. Williams is dividing construction paper into fourths. How many fourths can she make from 5 pieces of construction paper?
Answer:
The number of fourths can she make from 5 pieces of construction paper is 20 fourths.
Explanation:
Here, Mrs. Williams is dividing construction paper into fourths, so the number of fourths can she make from 5 pieces of construction paper is 5 ÷ \(\frac{1}{4}\) which is 5 × 4 = 20.
Question 4.
Use the chart below to answer the following questions.
Donnie’s Diner Lunch Menu
|
Food |
Serving Size |
|
Hamburger |
lb |
|
Pickles |
pickle |
| Potato chips |
bag |
| Chocolate milk |
cup |
a. How many hamburgers can Donnie make with 6 pounds of hamburger meat?
Answer:
The number of hamburgers can Donnie make with 6 pounds of hamburger meat is 18 hamburgers.
Explanation:
The number of hamburgers can Donnie make with 6 pounds of hamburger meat is 6 ÷ \(\frac{1}{3}\) which is 6 × 3 = 18 hamburgers.
b. How many pickle servings can be made from a jar of 15 pickles?
Answer:
The number of pickle servings can be made from a jar of 15 pickles is 60 pickles.
Explanation:
The number of pickle servings can be made from a jar of 15 pickles is 15 ÷ \(\frac{1}{4}\) which is 15 × 4 = 60 pickles
c. How many servings of chocolate milk can he serve from a gallon of milk?
Answer:
The number of servings of chocolate milk can he serve from a gallon of milk is 32 servings of chocolate milk..
Explanation:
The number of servings of chocolate milk can he serve from a gallon of milk is, as 1 gallon is 16 cups and 16 ÷ \(\frac{1}{2}\) which is 16 × 2 = 32 servings of chocolate milk.
Question 5.
Three gallons of water fill \(\frac{1}{4}\) of the elephant’s pail at the zoo. How much water does the pail hold?
Answer:
The pail holds 12 gallons.
Explanation:
Here, Three gallons of water fill \(\frac{1}{4}\) of the elephant’s pail at the zoo, so the pail holds 3 ÷ \(\frac{1}{4}\) which is 3 × 4 = 12 gallons.
Eureka Math Grade 5 Module 4 Lesson 25 Exit Ticket Answer Key
Question 1.
Draw a tape diagram and a number line to solve. Fill in the blanks that follow.
a. 5 ÷ \(\frac{1}{2}\) = _________
There are ____ halves in 1 whole.
There are ____ halves in 5 wholes.
5 is \(\frac{1}{2}\) of what number? _______
Answer:
5 ÷ \(\frac{1}{2}\) = 10
There are 2 halves in 1 whole.
There are 10 halves in 5 wholes.
5 is \(\frac{1}{2}\) the number is 10
Explanation:
Given that 5 ÷ \(\frac{1}{2}\) which is 5 × 2 = 10. And there are 2 halves in 1 whole and there are 10 halves in 5 wholes.
b. 4 ÷ \(\frac{1}{4}\) = _________
There are ____ fourths in 1 whole.
There are ____ fourths in ____ wholes.
4 is \(\frac{1}{4}\) of what number? _______
Answer:
4 ÷ \(\frac{1}{4}\) = 16
There are 4 fourths in 1 whole.
There are 16 fourths in 4 wholes.
4 is \(\frac{1}{4}\) the number 16
Explanation:
Given that 4 ÷ \(\frac{1}{4}\) which is 4 × 4 = 16. And there are 4 fourths in 1 whole and there are 16 fourths in 4 wholes.
Question 2.
Ms. Leverenz is doing an art project with her class. She has a 3 foot piece of ribbon. If she gives each student an eighth of a foot of ribbon, will she have enough for her class of 22 students?
Answer:
Ms. Leverenz has 3 foot ribbon or 36 inches, so she have enough for her class 22 students.
Explanation:
Here, Ms. Leverenz is doing an art project with her class and she has a 3 foot piece of ribbon, which is 12 × 3 = 36 foot. and if she gives each student an eighth of a foot of ribbon which is \(\frac{8}{12}\) = 1.5 inches of ribbon. Here Ms. Leverenz gives each students 1.5 inches ribbon. Therefore she needs for 22 students which is 22 × 1.5 = 33 inches. So she has 3 foot ribbon or 36 inches, so she have enough for her class 22 students.
Eureka Math Grade 5 Module 4 Lesson 25 Homework Answer Key
Question 1.
Draw a tape diagram and a number line to solve. Fill in the blanks that follow.
a. 3 ÷ \(\frac{1}{3}\) = _________
There are ____ thirds in 1 whole.
There are ____ thirds in 3 wholes.
If 3 is \(\frac{1}{3}\), what is the whole? _______
Answer:
3 ÷ \(\frac{1}{3}\) = 9
There are 3 thirds in 1 whole.
There are 9 thirds in 3 wholes.
If 3 is \(\frac{1}{3}\), the whole is 9.
Explanation:
Given that 3 ÷ \(\frac{1}{3}\) which is 3 × 3 = 9. And there are 3 thirds in 1 whole and there are 9 thirds in 3 wholes.
b. 3 ÷ \(\frac{1}{4}\) = _________
There are ____ fourths in 1 whole.
There are ____ fourths in __ wholes.
If 3 is \(\frac{1}{4}\), what is the whole? _______
Answer:
3 ÷ \(\frac{1}{4}\) = 12
There are 4 fourths in 1 whole.
There are 12 fourths in 3 wholes.
If 3 is \(\frac{1}{4}\), the whole 12.
Explanation:
Given that 3 ÷ \(\frac{1}{4}\) which is 3 × 4 = 12. And there are 4 fourths in 1 whole and there are 12 fourths in 3 wholes.
c. 4 ÷ \(\frac{1}{3}\) = _________
There are ____ thirds in 1 whole.
There are ____ thirds in __ wholes.
If 4 is \(\frac{1}{3}\), what is the whole? _______
Answer:
4 ÷ \(\frac{1}{3}\) = 12
There are 3 thirds in 1 whole.
There are 12 thirds in 4 wholes.
If 4 is \(\frac{1}{3}\), the whole 12.
Explanation:
Given that 4 ÷ \(\frac{1}{3}\) which is 4 × 3 = 12. And there are 3 thirds in 1 whole and there are 12 thirds in 4 wholes.
d. 5 ÷ \(\frac{1}{4}\) = _________
There are ____ fourths in 1 whole.
There are ____ fourths in __ wholes.
If 5 is \(\frac{1}{4}\), what is the whole? _______
Answer:
5 ÷ \(\frac{1}{4}\) = 20
There are 4 fourths in 1 whole.
There are 20 fourths in 5 wholes.
If 5 is \(\frac{1}{4}\), the whole is 20.
Explanation:
Given that 5 ÷ \(\frac{1}{4}\) which is 5 × 4 = 20. And there are 4 fourths in 1 whole and there are 20 fourths in 5 wholes.
Question 2.
Divide. Then, multiply to check.
a. 2 ÷ \(\frac{1}{4}\)
Answer:
2 ÷ \(\frac{1}{4}\) = 8.
Explanation:
Given that 2 ÷ \(\frac{1}{4}\) which is 2 × 4 = 8. To check we will perform multiplication \(\frac{1}{4}\) × 8 which is 2.
b. 6 ÷ \(\frac{1}{2}\)
Answer:
6 ÷ \(\frac{1}{2}\) = 12.
Explanation:
Given that 6 ÷ \(\frac{1}{2}\) which is 6 × 2 = 12. To check we will perform multiplication \(\frac{1}{2}\) × 12 which is 6.
c. 5 ÷ \(\frac{1}{4}\)
Answer:
5 ÷ \(\frac{1}{4}\) = 20.
Explanation:
Given that 5 ÷ \(\frac{1}{4}\) which is 5 × 4 = 20. To check we will perform multiplication \(\frac{1}{4}\) × 20 which is 5.
d. 5 ÷ \(\frac{1}{8}\)
Answer:
5 ÷ \(\frac{1}{8}\) = 40.
Explanation:
Given that 5 ÷ \(\frac{1}{8}\) which is 5 × 8 = 40. To check we will perform multiplication \(\frac{1}{8}\) × 40 which is 5.
e. 6 ÷ \(\frac{1}{3}\)
Answer:
6 ÷ \(\frac{1}{3}\) = 18.
Explanation:
Given that 6 ÷ \(\frac{1}{3}\) which is 6 × 3 = 18. To check we will perform multiplication \(\frac{1}{3}\) × 18 which is 6.
f. 3 ÷ \(\frac{1}{6}\)
Answer:
3 ÷ \(\frac{1}{6}\) = 18.
Explanation:
Given that 3 ÷ \(\frac{1}{6}\) which is 3 × 6 = 18. To check we will perform multiplication \(\frac{1}{6}\) × 18 which is 3.
g. 6 ÷ \(\frac{1}{5}\)
Answer:
6 ÷ \(\frac{1}{5}\) = 30.
Explanation:
Given that 6 ÷ \(\frac{1}{5}\) which is 6 × 5 = 30. To check we will perform multiplication \(\frac{1}{5}\) × 30 which is 6.
h. 6 ÷ \(\frac{1}{10}\)
Answer:
6 ÷ \(\frac{1}{10}\) = 60.
Explanation:
Given that 6 ÷ \(\frac{1}{10}\) which is 6 × 10 = 60. To check we will perform multiplication \(\frac{1}{10}\) × 60 which is 6.
Question 3.
A principal orders 8 sub sandwiches for a teachers’ meeting. She cuts the subs into thirds and puts the mini-subs onto a tray. How many mini-subs are on the tray?
Answer:
There will be 24 mini-subs are on the tray.
Explanation:
Given there are 8 sub sandwiches for a teachers meeting and each sandwich cuts into third. So 1 ÷ \(\frac{1}{3}\) which is 1 × 3 = 3 as there are 8 sub sandwiches, so there will be 8 × 3 = 24 mini-subs are on the tray.
Question 4.
Some students prepare 3 different snacks. They make \(\frac{1}{8}\) pound bags of nut mix, \(\frac{1}{4}\) pound bags of cherries, and \(\frac{1}{6}\) pound bags of dried fruit. If they buy 3 pounds of nut mix, 5 pounds of cherries, and 4 pounds of dried fruit, how many of each type of snack bag will they be able to make?
Answer:
There are 24 nut mix, 20 cherry bags and 24 dried fruits.
Explanation:
As some students prepare 3 different snacks and they make \(\frac{1}{8}\) pound bags of nut mix and they will be able to make number of nut mix bag is 3 ÷ \(\frac{1}{8}\) which is 3 × 8 = 24, and \(\frac{1}{4}\) pound bags of cherries they will be able to make number of cherries bag is 5 ÷ \(\frac{1}{4}\) which is 5 × 4 = 20 , and \(\frac{1}{6}\) pound bags of dried fruit and they will be able to make number of bags of dried fruit is 4 ÷ \(\frac{1}{6}\) which is 4 × 6 = 24. So there are 24 nut mix, 20 cherry bags and 24 dried fruits.