Engage NY Eureka Math 3rd Grade Module 7 Lesson 26 Answer Key
Eureka Math Grade 3 Module 7 Lesson 26 Pattern Sheet Answer Key
Multiply.
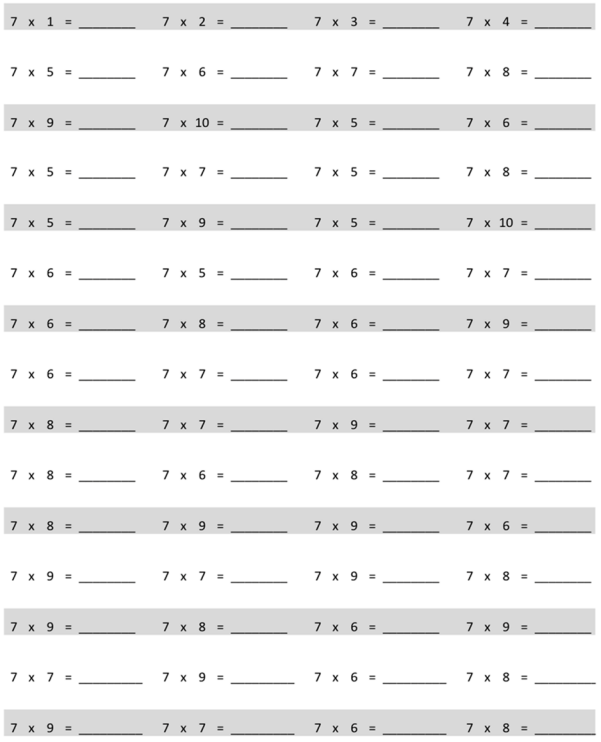
multiply by 7 (6–10)
Answer:

Explanation:
7 × 6 = 42
7 × 7 = 49
7 × 8 = 56
7 × 9 = 63
7 × 10 = 70.
Eureka Math Grade 3 Module 7 Lesson 26 Problem Set Answer Key
Question 1.
Collect the area measurements of your classmates’ robot bodies. Make a line plot using everyone’s area measurements.
Areas of Robot Bodies

a. How many different measurements are on the line plot? Why are the measurements different?
b. What does this tell you about the relationship between area and perimeter?
Answer:
a. 
There are four different kinds of measurements represented on the number line. They are different in values because the values of every rectangle is different from each other.
b. Perimeter is the measurement of the distance around a shape. Area is the measurement of space inside a shape. Area and Perimeter are not having any relationship because they are totally two different things. Perimeter is going to be more than the area of the rectangle.
Explanation:
a.
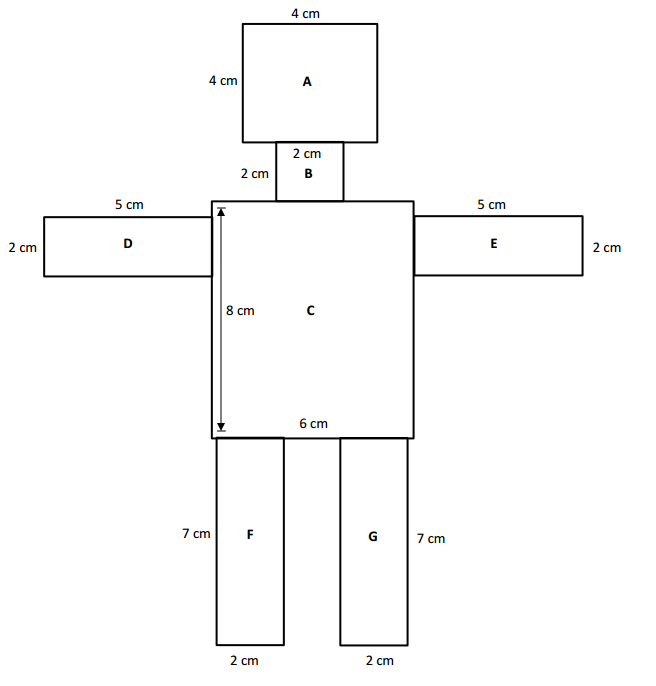
Area of the A rectangle = Length × Width = 4cm × 4cm = 16 square cm.
Area of the B rectangle = Length × Width = 2cm × 2cm = 16 square cm.
Area of the C rectangle = Length × Width = 8cm × 6cm = 48 square cm.
Area of the D rectangle = Length × Width = 5cm × 2cm = 10 square cm.
Area of the E rectangle = Length × Width = 5cm × 2cm = 10 square cm.
Area of the F rectangle = Length × Width = 7cm × 2cm = 14 square cm.
Area of the G rectangle = Length × Width = 7cm × 2cm = 14 square cm.
There are four different kinds of measurements represented on the number line. They are different in values because the values of every rectangle is different from each other.
b. Perimeter is the measurement of the distance around a shape. Area is the measurement of space inside a shape.
For Example : If a rectangle having length as 2cm and width as 1cm.
Perimeter = 2 (Length + Width) = 2 ( 2cm + 1cm) = 2 × 3cm = 6cm.
Area = length × Width = 2cm × 1cm = 2 square cm.
Area and Perimeter are not having any relationship because they are totally two different things.
Question 2.
Measure and calculate the perimeter of your construction paper in inches. Show your work below.
Answer:
Perimeter of my construction paper = 80 inches.
Explanation:
This is my construction paper.
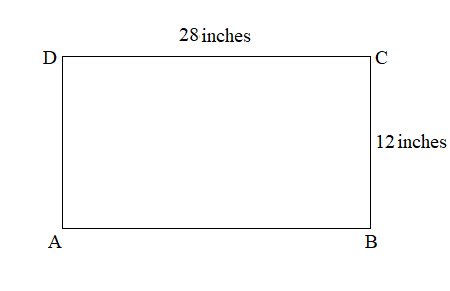
Length of my construction paper = 28 inches.
Width of my construction paper = 12 inches.
Perimeter of my construction paper = 2 ( Length + Width )
= 2 ( 28 inches + 12 inches )
= 2 × 40 inches
= 80 inches.
Question 3.
Sketch and label two shapes with the same perimeter from the robot’s environment. What do you notice about the way they look?
Answer:
Even though my two figure have the same Perimeter as 20cm yet they appearances are complete different in size and looks.
Explanation:
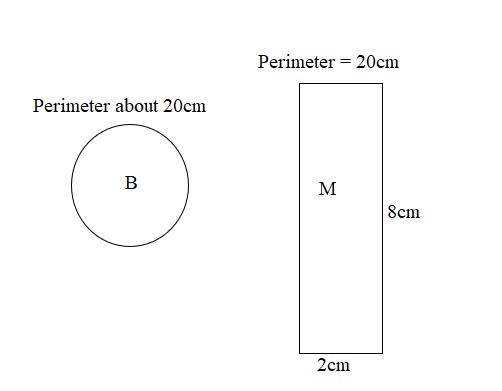
Same in perimeter the figure are yet different in size and appearance.
Question 4.
Write two or three sentences describing your robot and the environment in which it lives.
Answer:
My Robot name is Mr. Kool. He lives in machine land, where there are different kinds of Robots. He is very friendly in nature. He loves to help others in their works. He is taller than other Robots in his locality. He does all kinds of works and loves to be around people. He makes difficult works in a easy way.
Eureka Math Grade 3 Module 7 Lesson 26 Exit Ticket Answer Key
Question 1.
Use string to help you sketch a circle with a perimeter of about 15 centimeters.
Answer:
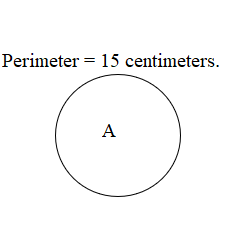
Explanation:
A figure is the circle having its Perimeter as 15 centimeters.
Question 2.
Estimate to draw a rectangle with a perimeter of 15 centimeters. Label the width and length.
Answer:
Perimeter of the ABCD rectangle = 15 centimeters.
Explanation:
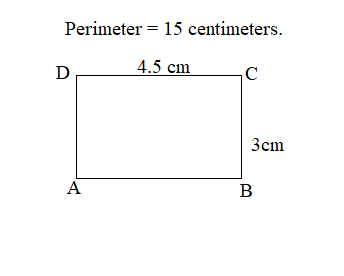
Length of the ABCD rectangle = 4.5cm
Width of the ABCD rectangle = 3cm
Perimeter of the ABCD rectangle = 2 ( Length + Width )
= 2 ( 4.5cm + 3cm )
= 2 × 7.5cm
= 15 centimeters.
Eureka Math Grade 3 Module 7 Lesson 26 Homework Answer Key
Question 1.
Use Rectangles A and B to answer the questions below.
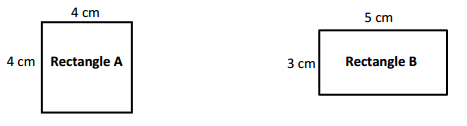
a. What is the perimeter of Rectangle A?
b. What is the perimeter of Rectangle B?
c. What is the area of Rectangle A?
d. What is the area of Rectangle B?
e. Use your answers to parts (a–d) to help you explain the relationship between area and perimeter.
Answer:
a. Perimeter of the Rectangle A = 16cm.
b. Perimeter of the Rectangle B = 16cm.
c. Area of the Rectangle A = 16 Square cm.
d. Area of the Rectangle B = 15 square cm.
e. The Perimeter of Rectangle A and Rectangle B are same 16cm. The Area of the Rectangle A is 16 square cm and Rectangle B is 15 square cm. There is no connection between the Perimeter and the Area. It is observed that the Perimeter values are more than the Area values of the rectangles.
Explanation:
a. 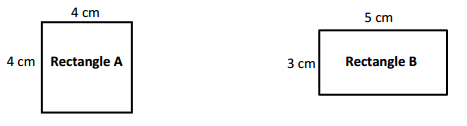
Length of the Rectangle A = 4cm
Width of the Rectangle A = 4cm
Perimeter of the Rectangle A = 2 ( Length + Width )
= 2 ( 4cm + 4cm )
= 2 × 8cm
= 16cm.
b. Length of the Rectangle B = 5cm
Width of the Rectangle B = 3cm
Perimeter of the Rectangle B = 2 ( Length + Width )
= 2 ( 5cm + 3cm )
= 2 × 8cm
= 16cm.
c. Length of the Rectangle A = 4cm
Width of the Rectangle A = 4cm
Area of the Rectangle A = Length × Width
= 4cm × 4cm
= 16 Square cm.
d. Length of the Rectangle B = 5cm
Width of the Rectangle B = 3cm
Area of the Rectangle B = Length × Width
= 5cm × 3cm
= 15 square cm.
e. There is no connection between the Perimeter and the Area. It is observed that the Perimeter values are more than the Area values of the rectangles.
Question 2.
Each student in Mrs. Dutra’s class draws a rectangle with whole number side lengths and a perimeter of 28 centimeters. Then, they find the area of each rectangle and create the table below.
| Area in Square Centimeters |
Number of Students |
| 13 | 2 |
| 24 | 1 |
| 33 | 3 |
| 40 | 5 |
| 45 | 4 |
| 48 | 2 |
| 49 | 2 |
a. Give two examples from Mrs. Dutra’s class to show how it is possible to have different areas for rectangles that have the same perimeter.
b. Did any students in Mrs. Dutra’s class draw a square? Explain how you know.
c. What are the side lengths of the rectangle that most students in Mrs. Dutra’s class made with a perimeter of 28 centimeters?
Answer:
a. 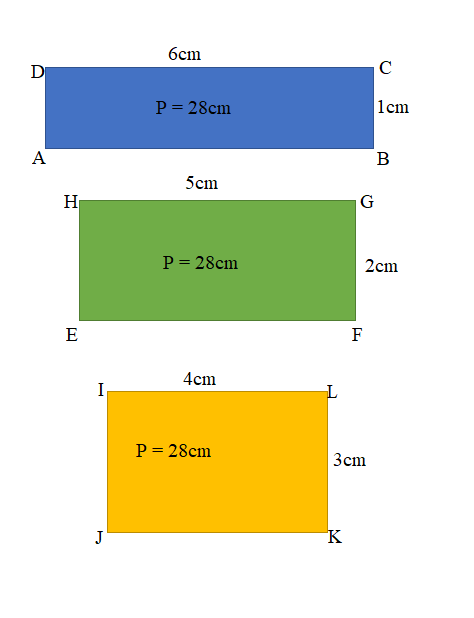
b. Yes, among all students in Mrs. Dutra’s class there is one student whose rectangle is said to be a square because all the sides are of 6cm each and have an area as 24 square cm.
c. 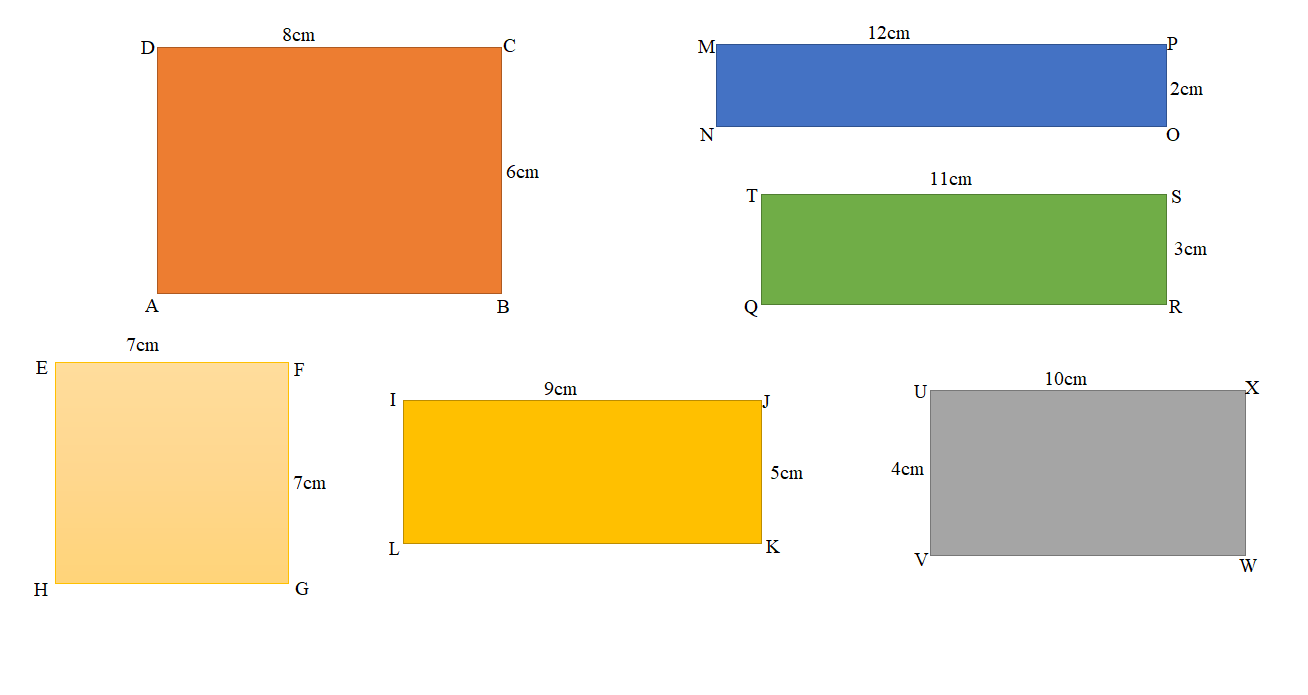
Explanation:
a. Here are two students rectangles having same perimeters yet different in areas for their rectangles are shown.
b. Area of the rectangles whose is 24 square cm, is said to be a square of having side length value as 6 cm.
c. Well, the side lengths of the rectangle that most students in Mrs. Dutra’s class made with a perimeter of 28 centimeters are: ( Length, Width)
(12,2); (11,3); (10,4); (9,5); (8,6); (7,7).