Engage NY Eureka Math Geometry Module 1 Lesson 7 Answer Key
Eureka Math Geometry Module 1 Lesson 7 Example Answer Key
Examples
Example 1.
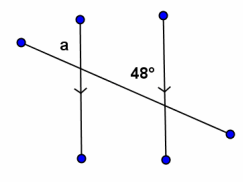
m∠a =
Answer:
m∠a=48°
Example 2.
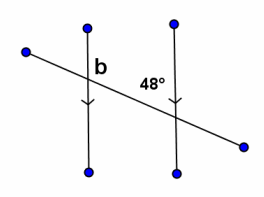
m∠b=
Answer:
m∠b=132°
Example 3.
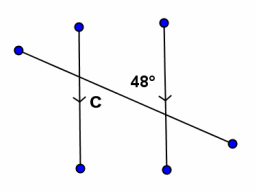
m∠c=
Answer:
m∠c=48°
Example 4.
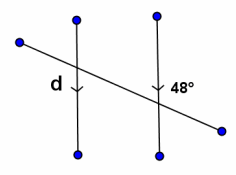
m∠d=
Answer:
m∠d=48°
Example 5.
An ___ is sometimes useful when solving for unknown angles. In this figure, we can use the auxiliary line to find the measures of ∠e and ∠f (how?) and then add the two measures together to find the measure of ∠W.
What is the measure of ∠W?
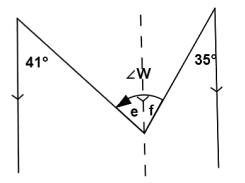
Answer:
An auxiliary line is sometimes useful when solving for unknown angles.
In this figure, we can use the auxiliary line to find the measures of ∠e and ∠f (how?) and then add the two measures together to find the measure of ∠W.
What is the measure of ∠W?
Answer:
m∠e=41°, m∠f=35°, m∠W=76°
Eureka Math Geometry Module 1 Lesson 7 Exercise Answer Key
Opening Exercise
Use the diagram at the right to determine x and y. \(\overleftrightarrow{A B}\) and \(\overleftrightarrow{C D}\) are straight lines.
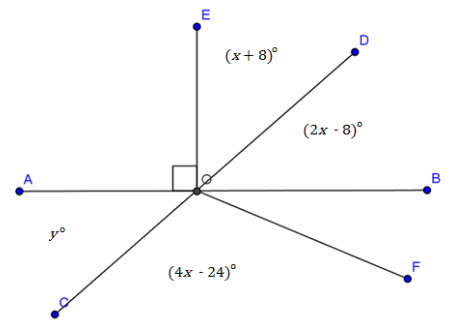
x =
y=
Answer:
x=30
y=52
Name a pair of vertical angles:
Answer:
∠AOC, ∠DOB
Find the measure of ∠BOF. Justify your calculation.
Answer:
m∠BOF=32° Linear pairs form supplementary angles.
Discussion
Given line AB and line CD in a plane (see the diagram below), a third line EF is called a transversal if it intersects (AB) ⃡ at a single point and intersects (CD) ⃡ at a single but different point. Line AB and line CD are parallel if and only if the following types of angle pairs are congruent or supplementary:
→ Corresponding angles are equal in measure.
Answer:
∠a and ∠e , ∠d and ∠h, etc.
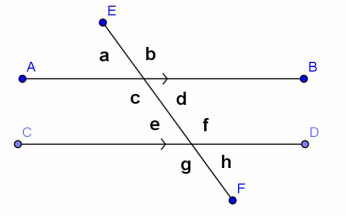
→ Alternate interior angles are equal in measure.
Answer:
∠c and ∠f, ∠d and ∠e
→ Same-side interior angles are supplementary.
Answer:
∠c and ∠e, ∠d and ∠f
Exercises 1–10
In each exercise below, find the unknown (labeled) angles. Give reasons for your solutions.
Exercise 1.

m∠a=
Answer:
m∠a=53°
If parallel lines are cut by a transversal, then corresponding angles are equal in measure.
m∠b=
Answer:
m∠b=53°
Vertical angles are equal in measure.
m∠c=
Answer:
m∠c=127°
If parallel lines are cut by a transversal, then interior angles on the same side are supplementary.
Exercise 2.

m∠d=
Answer:
m∠d=145°
Linear pairs form supplementary angles;
if parallel lines are cut by a transversal, then alternate interior angles are equal in measure.
Exercise 3.
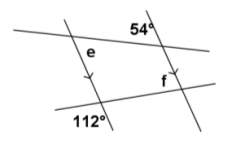
m∠e=
Answer:
m∠e=54°
If parallel lines are cut by a transversal, then alternate interior angles are equal in measure.
m∠f=
Answer:
m∠f=68°
Vertical angles are equal in measure;
if parallel lines are cut by a transversal, then interior angles on the same side are supplementary.
Exercise 4.
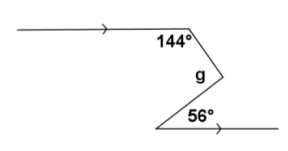
m∠g=
Answer:
m∠g=92°
Vertical angles are equal in measure;
if parallel lines are cut by a transversal, then interior angles on the same side are supplementary.
Exercise 5.
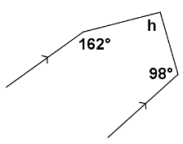
m∠h=
Answer:
m∠h=100°
If parallel lines are cut by a transversal, then interior angles on the same side are supplementary.
Exercise 6.

m∠i=
Answer:
m∠i=114°
Linear pairs form supplementary angles;
if parallel lines are cut by a transversal, then alternate interior angles are equal in measure.
Exercise 7.
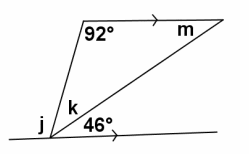
m∠j=
Answer:
m∠j=92°
If parallel lines are cut by a transversal, then alternate interior angles are equal in measure.
m∠k=
Answer:
m∠k=42°
Consecutive adjacent angles on a line sum to 180°.
m∠m=
Answer:
m∠m=46°
If parallel lines are cut by a transversal, then alternate interior angles are equal in measure.
Exercise 8.

m∠n=
Answer:
m∠n=81°
If parallel lines are cut by a transversal, then corresponding angles are equal in measure.
Exercise 9.
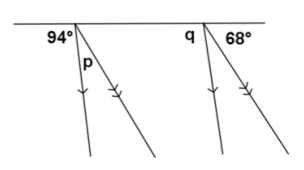
m∠p=
Answer:
m∠p=18°
Consecutive adjacent angles on a line sum to 180°.
m∠q=
Answer:
m∠q=94°
If parallel lines are cut by a transversal, then corresponding angles are equal in measure.
Exercise 10.
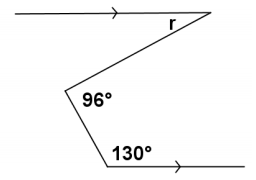
m∠r=
Answer:
m∠r=46°
If parallel lines are cut by a transversal, then interior angles on the same side are supplementary; if parallel lines are cut by a transversal, then alternate interior angles are equal in measure.
Eureka Math Geometry Module 1 Lesson 7 Problem Set Answer Key
Find the unknown (labeled) angles. Give reasons for your solutions.
Question 1.
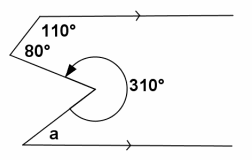
m∠a=
Answer:
m∠a=40°
If parallel lines are cut by a transversal, then alternate interior angles are equal in measure.
Question 2.

m∠b=
Answer:
m∠b=48°
If parallel lines are cut by a transversal, then corresponding angles are equal in measure.
m∠c=
Answer:
m∠c=46°
Vertical angles are equal in measure;
if parallel lines are cut by a transversal, then alternate interior angles are equal in measure.
Exercise 3.
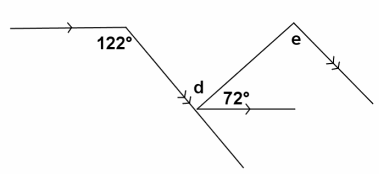
m∠d=
Answer:
m∠d=50°
If parallel lines are cut by a transversal, then alternate interior angles are equal in measure.
m∠e=
Answer:
m∠e=50°
If parallel lines are cut by a transversal, then alternate interior angles are equal in measure.
Exercise 4.

m∠f=
Answer:
m∠f=82°
If parallel lines are cut by a transversal, then interior angles on the same side are supplementary; vertical angles are equal in measure.
Eureka Math Geometry Module 1 Lesson 7 Exit Ticket Answer Key
Determine the value of each variable.
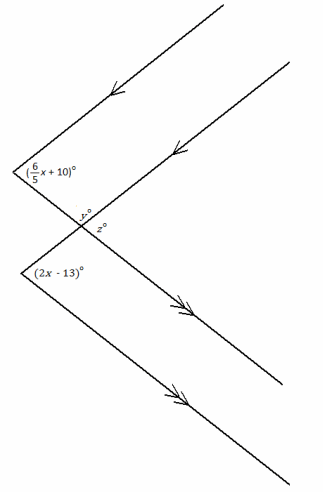
x =
y =
z =
Answer:
x= 28.75
y=135.5
z=44.5