Engage NY Eureka Math Geometry Module 1 Lesson 26 Answer Key
Eureka Math Geometry Module 1 Lesson 26 Exercise Answer Key
Exercises
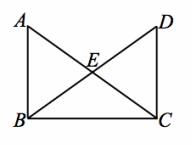
Exercise 1.
Given: \(\overline{A B}\) ⊥\(\overline{B C}\) ,\(\overline{B C}\) ⊥\(\overline{D C}\)
\(\overline{D B}\) bisects ∠ABC, \(\overline{A C}\) bisects ∠DCB
EB=EC
Prove: △BEA≅ △CED
Answer:
\(\overline{A B}\) ⊥\(\overline{B C}\) , \(\overline{B C}\) ⊥\(\overline{D C}\) Given
m∠ABC=90°, m∠DCB=90° Definition of perpendicular lines
m∠ABC=m∠DCB Transitive property
\(\overline{D B}\) bisects ∠ABC, \(\overline{A C}\) bisects ∠DCB Given
m∠ABE=45°, m∠DCE=45° Definition of an angle bisector
EB=EC Given
m∠AEB=m∠DEC Vertical angles are equal in measure.
△BEA≅ △CED ASA
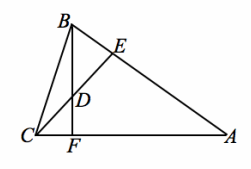
Exercise 2.
Given: \(\overline{B F}\) ⊥\(\overline{A C}\) ,\(\overline{C E}\) ⊥\(\overline{A B}\)
AE=AF
Prove: △ACE≅ △ABF
Answer:
\(\overline{B F}\) ⊥\(\overline{A C}\) , \(\overline{C E}\) ⊥\(\overline{A B}\) Given
m∠BFA=90°, m∠CEA=90° Definition of perpendicular
AE=AF Given
m∠A=m∠A Reflexive property
△ACE≅ △ABF ASA
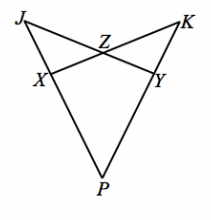
Exercise 3.
Given: XJ=YK,PX=PY,∠ZXJ≅∠ZYK
Prove: JY=KX
Answer:
XJ=YK, PX=PY, ∠ZXJ≅∠ZYK Given
\(\overline{J P}\) ≅ \(\overline{K P}\) Segment addition
m∠JZX=m∠KZY Vertical angles are equal in measure.
△JZX≅△KZY AAS
∠J≅∠K Corresponding angles of congruent triangles are congruent.
∠P≅∠P Reflexive property
△PJY≅ △PKX AAS
\(\overline{J Y}\) ≅ \(\overline{K X}\) Corresponding sides of congruent triangles are congruent.
JY=KX Definition of congruent segments
Exercise 4.
Given: JK=JL, \(\overline{J K}\) || \(\overline{X Y}\)
Prove: XY=XL
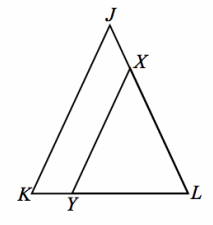
Answer:
JK=JL Given
m∠K=m∠L Base angles of an isosceles triangle are equal in measure.
\(\overline{J K}\) ∥\(\overline{X Y}\) Given
m∠K=m∠XYL When two parallel lines are cut by a transversal, corresponding angles are equal in measure.
m∠XYL=m∠L Transitive property
XY=XL If two angles of a triangle are congruent, then the sides opposite the angles are equal in length.
Exercise 5.
Given: ∠1≅∠2, ∠3≅∠4
Prove: \(\overline{A C}\) ≅ \(\overline{B D}\)
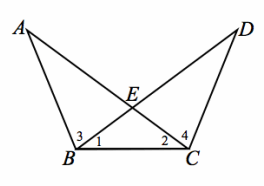
Answer:
∠1≅∠2 Given
\(\overline{B E}\) ≅ \(\overline{C E}\) When two angles of a triangle are congruent, it is an isosceles triangle.
∠3≅∠4 Given
∠AEB≅∠DEC Vertical angles are congruent.
△ABE≅ △DCE ASA
∠A≅∠D Corresponding angles of congruent triangles are congruent.
m∠ABC=m∠1+m∠3;
m∠DCB=m∠2+m∠4 Angle addition
m∠ABC=m∠DCB Substitution
\(\overline{B C}\) ≅ \(\overline{B C}\) Reflexive property
△ABC≅ △DCB AAS
\(\overline{A C}\) ≅ \(\overline{B D}\) Corresponding sides of congruent triangles are congruent
Exercise 6.
Given: m∠1=m∠2, m∠3=m∠4, AB=AC
Prove: (a) △ABD≅ △ACD
(b) ∠5≅∠6
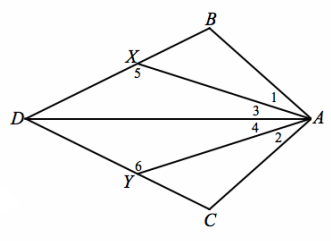
Answer:
m∠1=m∠2, m∠3=m∠4,
AB=AC Given
m∠1+m∠3=m∠DAB,
m∠2+m∠4=m∠DAC Angle addition postulate
m∠DAB=m∠DAC Substitution property of equality
AD=AD Reflexive property
△ABD≅ △ACD SAS
∠BDA≅∠CDA Corresponding angles of congruent triangles are congruent.
△DXA≅ △DYA ASA
∠5≅∠6 Corresponding angles of congruent triangles are congruent.
Eureka Math Geometry Module 1 Lesson 26 Problem Set Answer Key
Use your knowledge of triangle congruence criteria to write a proof for the following:
In the figure, \(\overline{R X}\) and \(\overline{R Y}\) are the perpendicular bisectors of \(\overline{A B}\) and \(\overline{A C}\) , respectively.
Prove: (a) △RAX≅ △RBX
(b) \(\overline{R A}\) ≅ \(\overline{R B}\) ≅ \(\overline{R C}\)
Answer:
\(\overline{R X}\) is the perpendicular bisector of \(\overline{A B}\) . Given
m∠RXA=90°, m∠RXB=90° Definition of perpendicular bisector
\(\overline{A X}\) ≅ \(\overline{X B}\) Definition of perpendicular bisector
\(\overline{R X}\) ≅ \(\overline{R X}\) Reflexive property
△RAX≅ △RBX SAS
\(\overline{R Y}\) is the perpendicular bisector of \(\overline{A C}\) Given
m∠RYA=90°, m∠RYC=90° Definition of perpendicular bisector
\(\overline{A Y}\) ≅ \(\overline{Y C}\) Definition of perpendicular bisector
\(\overline{R Y}\) ≅\(\overline{R Y}\) Reflexive property
△RAY≅ △RCY SAS
\(\overline{R A}\) ≅\(\overline{R B}\) , \(\overline{R A}\) ≅ \(\overline{R C}\) Corresponding sides of congruent triangles are congruent.
\(\overline{R A}\) ≅ \(\overline{R B}\) ≅ \(\overline{R C}\) Transitive property
Eureka Math Geometry Module 1 Lesson 26 Exit Ticket Answer Key
Identify the two triangle congruence criteria that do NOT guarantee congruence. Explain why they do not guarantee congruence, and provide illustrations that support your reasoning.
Answer:
Students should identify AAA and SSA as the two types of criteria that do not guarantee congruence. Appropriate illustrations should be included with their justifications.