Engage NY Eureka Math Geometry Module 1 Lesson 20 Answer Key
Eureka Math Geometry Module 1 Lesson 20 Example Answer Key
Example 1.
In each figure below, the triangle on the left has been mapped to the one on the right by a 240° rotation about P. Identify all six pairs of corresponding parts (vertices and sides).
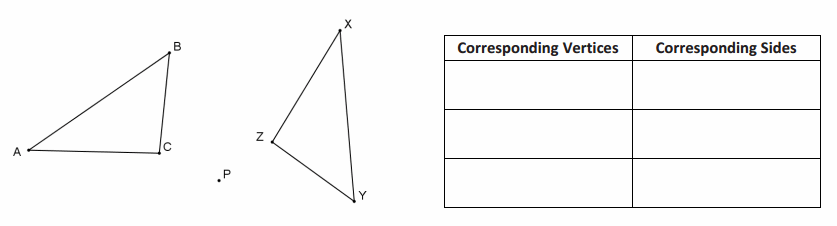
Answer:
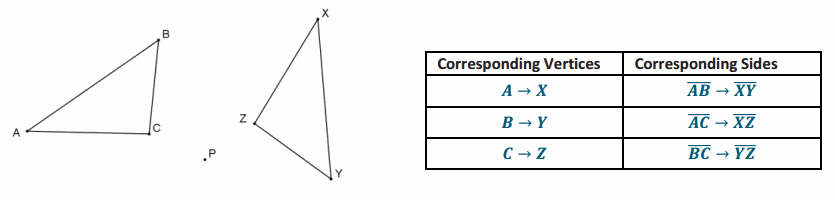
What rigid motion mapped △ABC onto △XYZ? Write the transformation in function notation.
Answer:
RP,240°(△ABC)→ △XYZ
Example 2.
Given a triangle with vertices A, B, and C, list all the possible correspondences of the triangle with itself.
Answer:
A→A B→B C→C
A→A B→C C→B
A→B B→A C→C
A→B B→C C→A
A→C B→A C→B
A→C B→B C→A
Example 3.
Give an example of two quadrilaterals and a correspondence between their vertices such that (a) corresponding sides are congruent, but (b) corresponding angles are not congruent.

Answer:
A→J
B→K
C→L
D→M
Eureka Math Geometry Module 1 Lesson 20 Problem Set Answer Key
Given two triangles, one with vertices A, B, and C, and the other with vertices X, Y, and Z, there are six different correspondences of the first with the second.
a. One such correspondence is the following:
A→Z
B→X
C→Y
Write the other five correspondences.
Answer:
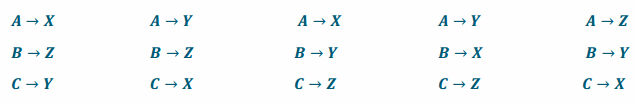
b. If all six of these correspondences come from congruences, then what can you say about △ABC?
Answer:
It must be equilateral.
c If two of the correspondences come from congruences, but the others do not, then what can you say about △ABC ?
Answer:
It must be isosceles and cannot be equilateral.
d. Why can there be no two triangles where three of the correspondences come from congruences, but the others do not?
Answer:
By part (c), if two correspondences come from congruences, then the triangle must be isosceles. A third correspondence implies that the triangles must be equilateral. But then all six correspondences would be congruences, contradicting that the others are not.
Question 2.
Give an example of two triangles and a correspondence between them such that (a) all three corresponding angles are congruent, but (b) corresponding sides are not congruent.
Answer:

A→E
B→D
C→F
Question 3.
Give an example of two triangles and a correspondence between their vertices such that (a) one angle in the first is congruent to the corresponding angle in the second, and (b) two sides of the first are congruent to the corresponding sides of the second, but (c) the triangles themselves are not congruent.
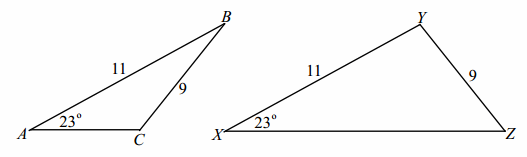
Answer:
A→X
B→Y
C→Z
Question 4.
Give an example of two quadrilaterals and a correspondence between their vertices such that (a) all four corresponding angles are congruent, and (b) two sides of the first are congruent to two sides of the second, but (c) the two quadrilaterals are not congruent.
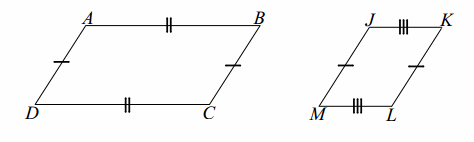
Answer:
A→J
B→K
C→L
D→M
Question 5.
A particular rigid motion, M, takes point P as input and gives point P’ as output. That is, M(P)=P’. The same rigid motion maps point Q to point Q’. Since rigid motions preserve distance, is it reasonable to state that
PP’=QQ’? Does it matter which type of rigid motion M is? Justify your response for each of the three types of rigid motion. Be specific. If it is indeed the case, for some class of transformations, that PP’=QQ’ is true for all P and Q, explain why. If not, offer a counterexample.
Answer:
This is not always true. A rotation around a vertex does not move each point the same distance. In a rigid motion, the distance that is preserved is within the figure distance. A reflection also does not satisfy PP’=QQ’ for all P and Q. Reflecting a figure over one of its sides does not move the points on the line of reflection, and other points are moved by a distance proportionate to their distance from the reflection line. A translation, however, does satisfy the condition that PP’=QQ’ for all P and Q.
Eureka Math Geometry Module 1 Lesson 20 Exit Ticket Answer Key
Question 1.
What is a correspondence? Why does a congruence naturally yield a correspondence?
Answer:
A correspondence between two triangles is a pairing of each vertex of one triangle with one and only one vertex of the other triangle. This pairing can be expanded to figures other than triangles. A congruence naturally yields a correspondence since a rigid motion maps each part of a figure to what we call a corresponding part of the image.
Question 2.
Each side of △XYZ is twice the length of each side of △ABC. Fill in the blanks below so that each relationship between lengths of sides is true.
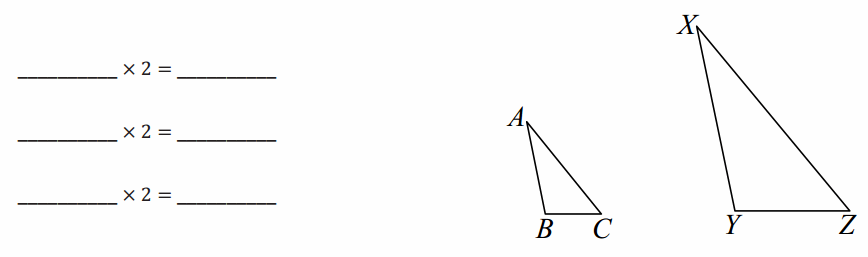
___ ×2 = ___
AB × 2 = XY
___ ×2 = ___
BC × 2 = YZ
___ ×2 = ___
CA ×2 = ZX