Engage NY Eureka Math Algebra 2 Module 2 Lesson 3 Answer Key
Eureka Math Algebra 2 Module 2 Lesson 3 Exercise Answer Key
Exercise 1.
Calculate jya(7°), jya(11°), jya(15°), and jya(18°) using Aryabhata’s formula’, round to the nearest integer, and add your results to the table below. Leave the rightmost column blank for now.
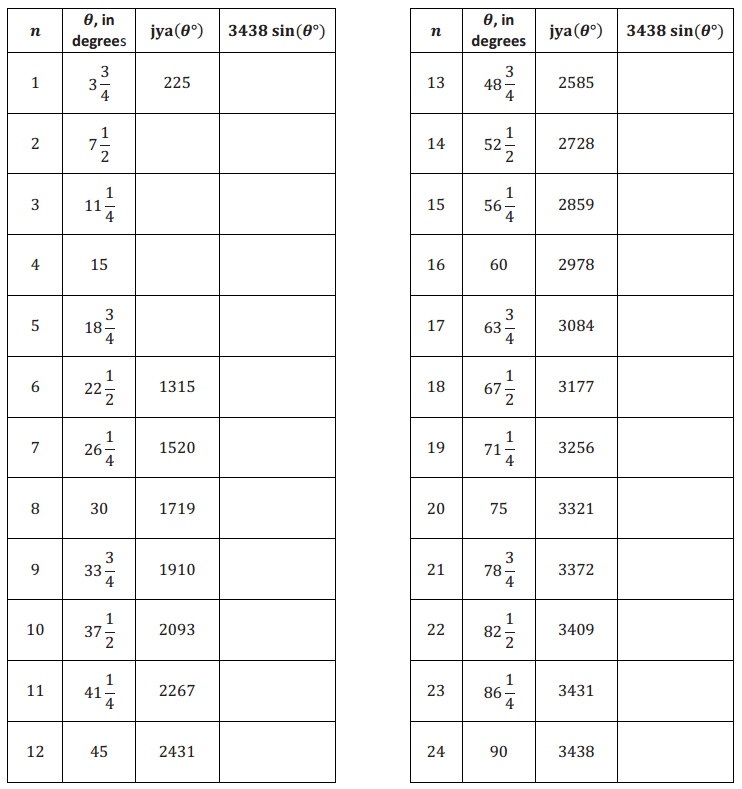
Answer:
Exercise 2.
Label the angle θ, jya(θ°), kojya(θ°), and r in the diagram shown below.
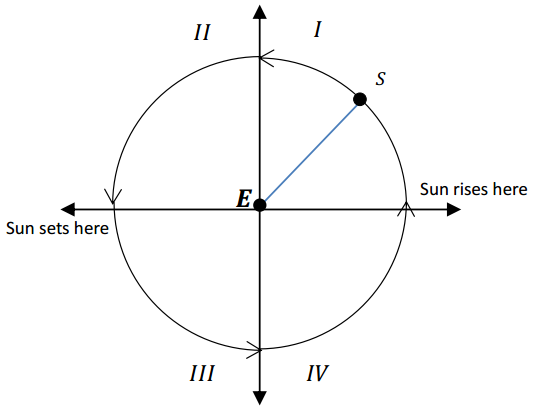
a. How does this relate to something you’ve done before?
Answer:
Jya and kojya are lengths of the sides of a right triangle. They are also like the height and co-height functions of the passenger car on a Ferris wheel.
b. How do jya(θ°) and kojya(θ°) relate to lengths we already know?
Answer:
From prior work with triangle trigonometry, jya(θ°) = r sin(θ°) and kojya(θ°) = r cos(θ°).
Exercise 3.
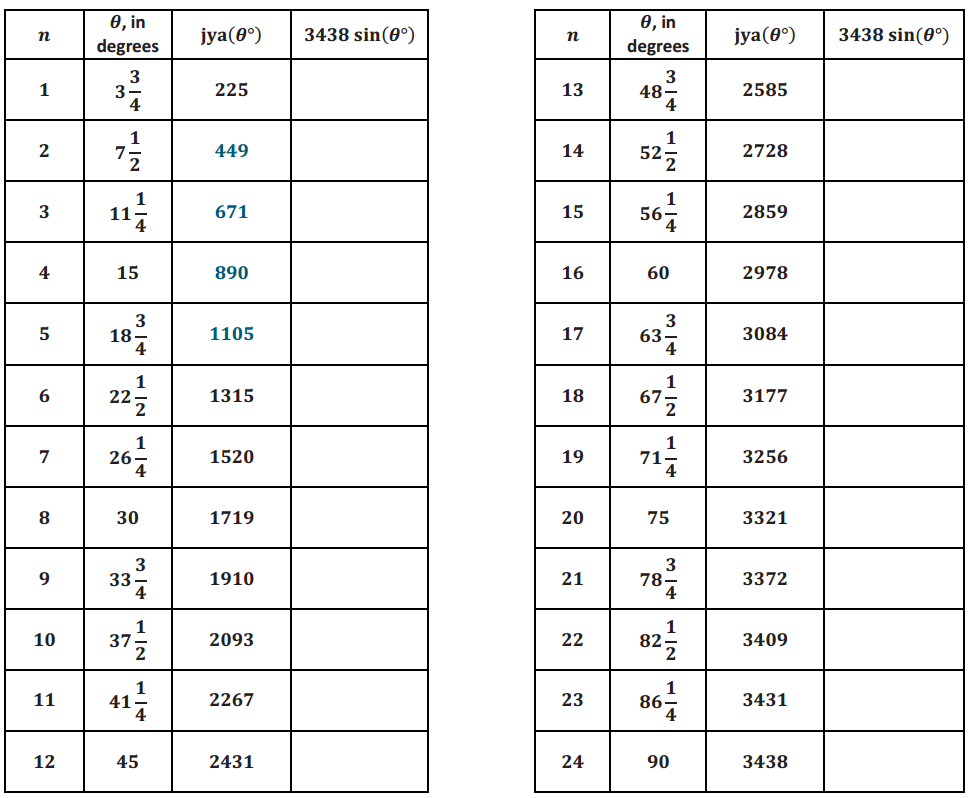
Use your calculator to compute r sin(θ°) for each value of θ in the table from Exercise 1, where r = 3438. Record this in the blank column on the right in Exercise 1, rounding to the nearest integer. How do Aryabhata’s approximated values from around the year 500 C.E. compare to the value we can calculate with our modern technology?
Answer:
The values are surprisingly close.
Exercise 4.
We will assume that the sun rises at 6:00 a.m., is directly overhead at 12:00 noon, and sets at 6:00 p.m. We measure the height of the sun by finding its vertical distance from the horizon line; the horizontal line that connects the easternmost point, where the sun rises, to the westernmost point, where the sun sets.
a. Using r = 3438, as Aryabhata did, find the height of the sun at the times listed in the following table:
| Time of day | Height |
| 6:00 a.m. | |
| 7:00 a.m. | |
| 8:00 a.m. | |
| 9:00 a.m. | |
| 10:00 a.m. | |
| 11:00 a.m. | |
| 12:00 p.m. |
Answer:
Given this scenario, the sun will move 15° each hour. Then the heights will be:
6:00 a.m. → jya(0°) = 0
7:00 a.m. → jya(15°) = 890
8:00 a.m. → jya(30°) = 1719
9:00 a.m. → jya(45°) = 2431
10:00 a.m. → jya(60°) = 2978
11:00 a.m. → jya(75°) = 3321
12:00 p.m. → jya(90°) = 3438
b. Now, find the height of the sun at the times listed in the following table using the actual distance from the earth to the sun, which is 93 million miles.
| Time of day | Height |
| 6:00 a.m. | |
| 7:00 a.m. | |
| 8:00 a.m. | |
| 9:00 a.m. | |
| 10:00 a.m. | |
| 11:00 a.m. | |
| 12:00 p.m. |
Answer:

Eureka Math Algebra 2 Module 2 Lesson 3 Problem Set Answer Key
Question 1.
An Indian astronomer noted that the angle of his line of sight to Venus measured 52°. We now know that the average distance from Earth to Venus is 162 million miles. Use Aryabhata’s table to estimate the apparent height of Venus. Round your answer to the nearest million miles.
Answer:
By the table, jya(52. 5°) = 2728. Since 162 ∙ \(\frac{\mathrm{jya}\left(52.5^{\circ}\right)}{3438}\) = 129, the apparent height is 129 million miles.
Question 2.
Later, the Indian astronomer saw that the angle of his line of sight to Mars measured 82°. We now know that the average distance from Earth to Mars is 140 million miles. Use Aryabhata’s table to estimate the apparent height of Mars. Round your answer to the nearest million miles.
Answer:
By the table, jya(82. 5°) = 3409. Since 140 ∙ \(\frac{\mathrm{jya}\left(82.5^{\circ}\right)}{3438}\) = 139, the apparent height is 139 million miles.
Question 3.
The moon orbits the earth in an elongated orbit, with an average distance of the moon from the earth of roughly 239,000 miles. It takes the moon 27.32 days to travel around the earth, so the moon moves with respect to the stars roughly 0. 5° every hour. Suppose that angle of inclination of the moon with respect to the observer measures 45° at midnight. As in Example 1, an observer is standing still and facing north. Use Aryabhata’s jya table to find the apparent height of the moon above the observer at the times listed in the table below, to the nearest thousand miles.
| Time (hour:min) | Angle of elevation θ, in degrees |
Height |
| 12:00 a.m. | ||
| 7:30 a.m. | ||
| 3:00 p.m. | ||
| 10:30 a.m. | ||
| 6:00 a.m. | ||
| 1:30 p.m. | ||
| 9:00 p.m. |
Answer:

Question 4.
George wants to apply Aryabhata’s method to estimate the height of the International Space Station, which orbits Earth at a speed of about 17, 500 miles per hour. This means that the space station makes one full rotation around Earth roughly every 90 mInutes. The space station maintains a low earth orbit, with an average distance from Earth of 238 miles.
a. George supposes that the space station is just visible on the eastern horizon at 12:00 midnight, so its apparent height at that time would be 0 miles above the horizon. Use Aryabhata’s jya table to find the apparent height of the space station above the observer at the times listed in the table below.
| Time (hour:min:sec) | Angle of elevation θ, in degrees |
Height |
| 12:00:00 a.m. | ||
| 12:03:00 a.m. | ||
| 12:07:30 a.m. | ||
| 12:11:15 a.m. | ||
| 12:15:00 a.m. | ||
| 12:18:45 a.m. | ||
| 12:22:30 a.m. |
Answer:

b. When George presents his solution to his classmate Jane, she tells him that his model isn’t appropriate for this situation. Is she correct? Explain how you know. (Hint: As we set up our model in the first discussion, we treated our observer as 1f he was the center of the orbit of the sun around the earth. In part (a) of this problem, we treated our observer as if she were the center of the orbit of the International Space Station around Earth. The radius of Earth is approximately 3,963 miles, the space station orbits about 238 miles above Earth’s surface, and the distance from Earth to the sun is roughly 93,000,000 mIles. Draw a picture of the earth and the path of the space station, and then compare that to the points with heights and rotation angles from part (a).)
Answer:
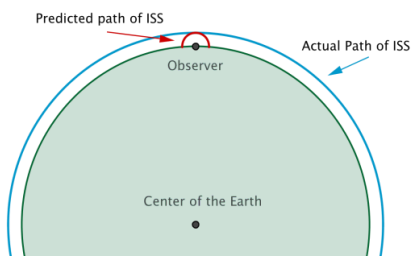
The semicircular path of the space station in this model will have a radius of 238 miles. However, because 3963 + 238 = 4201, the space station should have a radius of 4,201 miles. In this model, the space station starts at a point 238 miles to the east of the observer and crashes into Earth at a point 238 miles to the west of the observer. Thus, this is not an appropriate model to use for the height of the International Space Station.
The problem is that the radius of Earth is negligible in comparison to the distance of 93, 000,000 miles from the surface of Earth to the sun, but the radius of Earth is not negligible in comparison to the distance of 238 miles from the surface of Earth to the International Space Station.
Eureka Math Algebra 2 Module 2 Lesson 3 Exit Ticket Answer Key
Question 1.
Explain why counterclockwise is considered to be the positive direction of rotation In mathematics.
Answer:
Clocks were invented based on the movement of the shadows across a sundial. These shadows then move In the direction we call clockwise. The sun, on the other hand, moves in the opposite direction as the shadows, so the sun appears to move counterclockwise with respect to us if we are facing north in the Northern Hemisphere. Since our observations are based on the movement of the sun, the direction of the sun’s path, starting in the east, rising, and setting in the west, determined our conventions for the direction of rotation considered positive in the coordinate plane.
Question 2.
Suppose that you measure the angle of elevation of your line of sight with the sun to be 67. 5°. If we use the value of 1 astronomical unit (abbreviated AU) as the distance from the earth to the sun, use the portion of the jya table below to calculate the sun’s apparent height in astronomical units.

Answer:
The only value we need from the table is jya(67. 5°) = 3177. Since we are using a radius of 1 astronomical unit, the apparent height will be smaller than 1. We have:
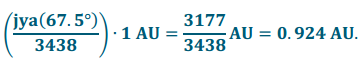
Eureka Math Algebra 2 Module 2 Lesson 3 Opening Answer Key
Why does it look like the sun moves across the sky?
Answer:
The sun essentially stays still, but the earth rotates on Its axis once every 24 hours; so, if an observer were standing in one place for 24 hours, it would appear that the sun becomes visible in the east, travels across the sky, and sets in the west.
Is the sun moving, or are you moving?
Answer:
Technically, both are moving, but the sun moves imperceptibly while an observer on the face of the earth rotates away from the sun. I would say that the observer is moving.
In ancient Greek mythology, the god Helios was the personification of the sun. He rode across the sky every day in his chariot led by four horses. Why do your answers make It believable that in ancient times people Imagined the sun was pulled across the sky each day?
Answer:
If we did not know that the earth rotated every day, then a reasonable explanation would be that the sun moved across the sky each day.
Eureka Math Algebra 2 Module 2 Lesson 3 Discussion Answer Key
→ Is there a connection between counterclockwise motion being considered to be positive and the naming of the quadrants on a standard coordinate system?

Answer:
Yes! The quadrants are ordered according to the (counterclockwise) path the sun takes, beginning when it rises from the east.
→ What does the circle’s radius, r, represent?
Answer:
The radius length r represents the distance between the center of the earth and the center of the sun.
→ How has the motion of the sun influenced the development of mathematics?
Answer:
The naming of the quadrants and the idea of measuring rotations counterclockwise make sense in terms of how we perceive the movement of stars and planets on Earth.
→ How is measuring the height of the sun like measuring the Ferris wheel passenger car height in the previous lessons?
Answer:
Both situations relate a vertical distance to a measurement of rotation from an initial reference point.