Engage NY Eureka Math Algebra 2 Module 2 Lesson 14 Answer Key
Eureka Math Algebra 2 Module 2 Lesson 14 Exploratory Challenge Exercise Answer Key
Exploratory Challenge/Exercises 1-5
Exercise 1.
Use your calculator to calculate each value of tan(x) to two decimal places in the table for your group.
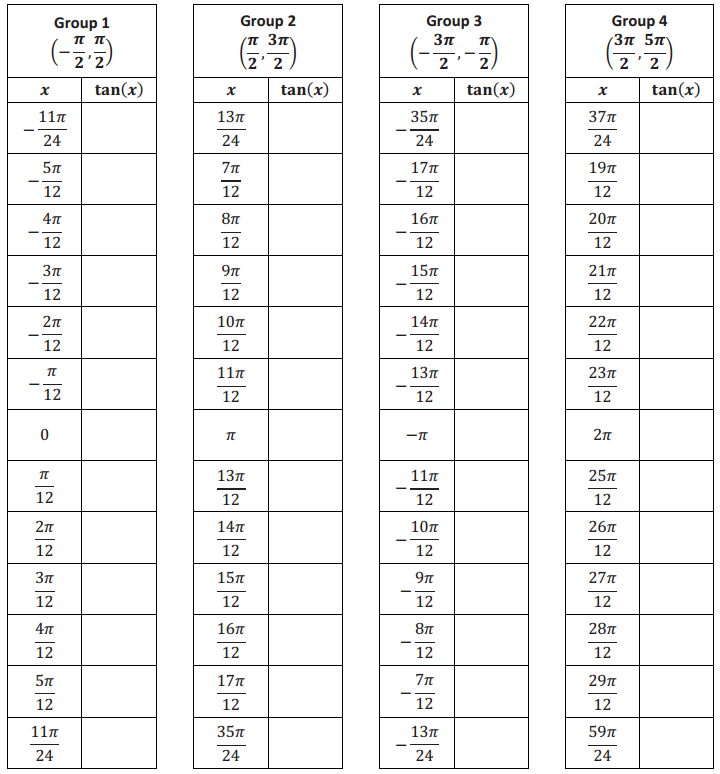
Answer:

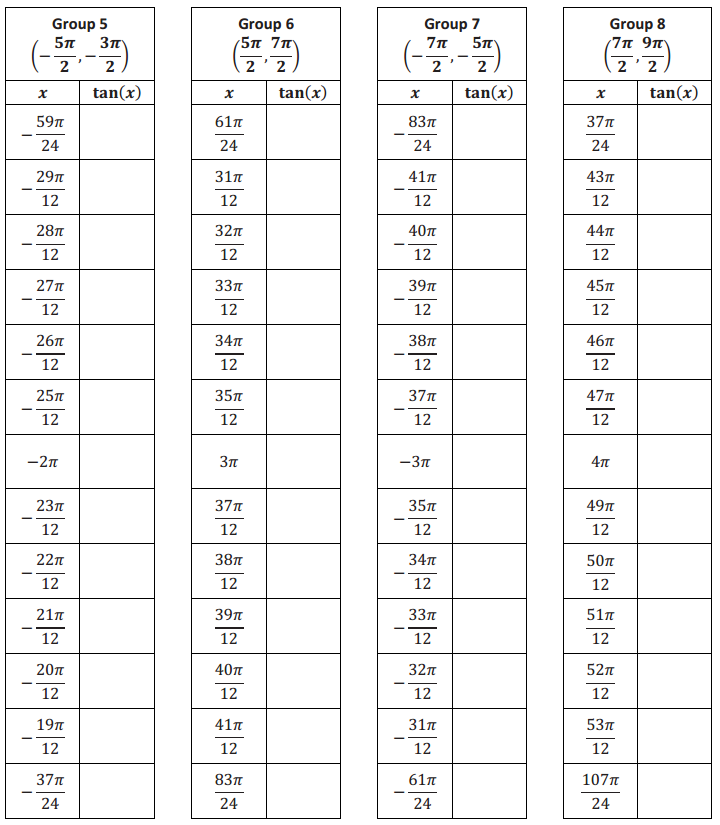
Answer:
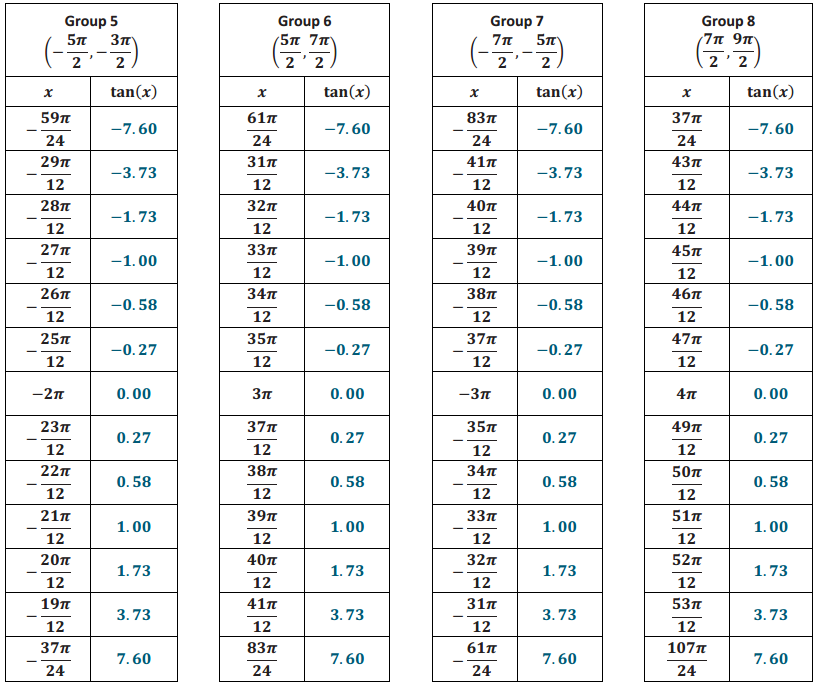
Exercise 2.
The tick marks on the axes provided are spaced in increments of \(\frac{\pi}{12}\). Mark the horizontal axis by writing the number of the left endpoint of your interval at the leftmost tick mark, the multiple of π that is in the middle of your interval at the point where the axes cross, and the number at the right endpoint of your interval at the rightmost tick mark. Fill in the remaining values at increments of \(\frac{\pi}{2}\)
Answer:
The x-axis from one such set of marked axes on the interval \(\left(\frac{\pi}{2}, \frac{3 \pi}{2}\right)\) is shown below.
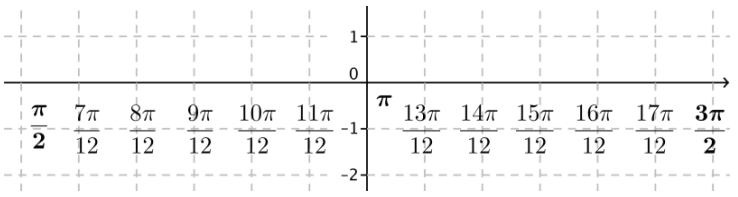
Exercise 3.
On your plot, sketch the graph of y = tan(x) on your specified interval by plotting the points in the table and connecting the points with a smooth curve. Draw the graph with a bold marker.
An example on the interval \(\left(\frac{\pi}{2}, \frac{3 \pi}{2}\right)\) is shown to the right.
Answer:
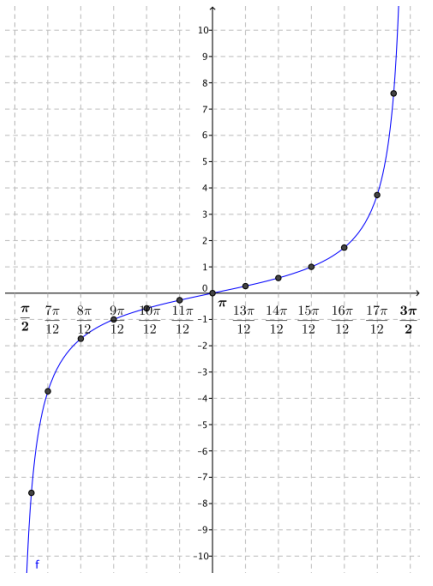
Exercise 4.
What happens to the graph near the edges of your interval? Why does this happen?
Answer:
Near the edges of the interval, x approaches a value where the tangent function is undefined. Since cos (\(\frac{\pi}{2}\) + kπ) = 0 for any integer k, the tangent is undefined at the edges of the interval we are graphing. As x gets near the edge of the interval, sin(x) gets close to either 1 or – 1, and cos(x) gets close to 0. Thus, tan(x) = \(\frac{\sin (x)}{\cos (x)}\) gets very far from zero, either in the positive or negative direction.
Exercise 5.
When you are finished, affix your graph to the board in the appropriate place, matching endpoints of intervals.
Answer:
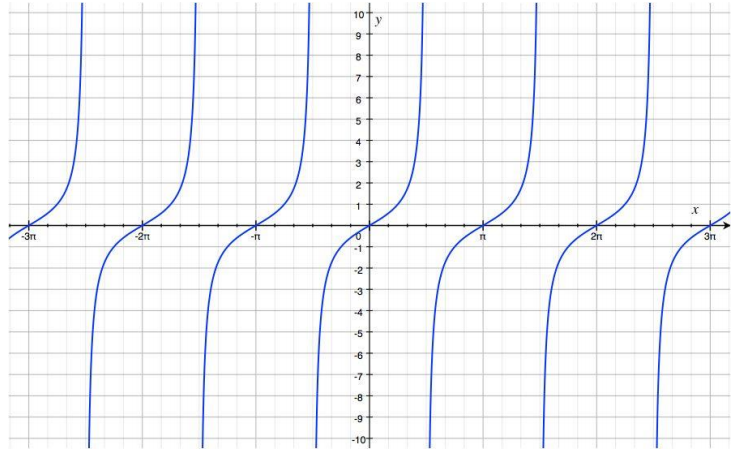
Exploratory Challenge 2/Exercises 6- 16
For each exercise below, let m = tan(θ) be the slope of the terminal ray in the definition of the tangent function, and let P = (x0, yo) be the intersection of the terminal ray with the unit circle after being rotated by θ radians for 0 < θ < \(\frac{\pi}{2}\). We know that the tangent of θ is the slope m of ![]() .
.
Exercise 6.
Let Q be the intersection of the terminal ray with the unit circle after being
rotated by θ + π radians.
a. What is the slope of im-9?
Answer:
Points P, O, and Q are collinear, so the slope of ![]() ‘is the same as the slope of
‘is the same as the slope of ![]() . Thus, the slope of
. Thus, the slope of ![]() is also m. Another approach would be to find that the coordinates of Q are (- x0, -yo), so the slope of ray
is also m. Another approach would be to find that the coordinates of Q are (- x0, -yo), so the slope of ray ![]() is \(\frac{y_{0}}{x_{0}}\), which is m.
is \(\frac{y_{0}}{x_{0}}\), which is m.
b. Find an expression for tan(θ + π) in terms of m.
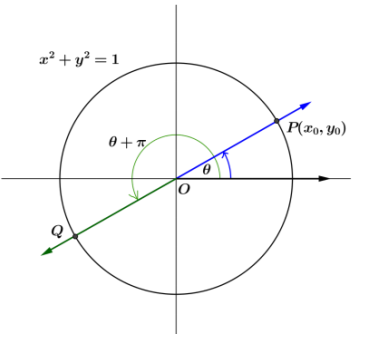
Answer:
tan(θ + π) = m
c. Find an expression for tan(θ + π) in terms of tan(θ).
Answer:
tan(θ + π) = tan(θ)
d. How can the expression in part (c) be seen in the graph of the tangent function?
Answer:
The pieces of the tangent function repeat every π units because tan(θ + π) = tan(θ).
Exercise 7.
Let Q be the intersection of the terminal ray with the unit circle after being rotated by – θ radians.
a. What is the slope of ![]() ?
?
Answer:
Ray ![]() is the reflection of ray
is the reflection of ray ![]() across the x-axis, so the coordinates of Q are (x0, – yo). Thus, the slope of
across the x-axis, so the coordinates of Q are (x0, – yo). Thus, the slope of ![]() is the opposite of the slope of
is the opposite of the slope of ![]() . Thus, the slope of
. Thus, the slope of ![]() is -m.
is -m.
b. Find an expression for tan(-θ) in terms of m.
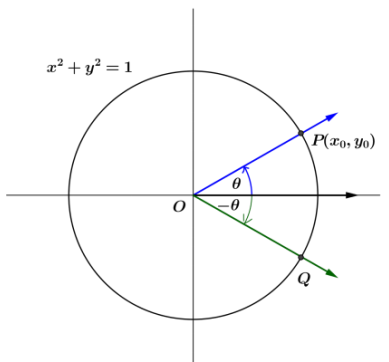
Answer:
tan(-θ) = – m
c. Find an expression for tan(-θ) in terms of tan(θ).
Answer:
tan(- θ) = – tan(θ)
d. How can the expression in part (c) be seen in the graph of the tangent function?
Answer:
The graph of the tangent function has rotational symmetry about the origin.
Exercise 8.
Is the tangent function an even function, an odd function, or neither? How can you tell your answer is correct from the graph of the tangent function?
Answer:
Because tan(-θ) = -tan(θ), the tangent function is odd. If the graph of the tangent function is rotated ir radians about the origin, there will appear to be no change in the graph.
Exercise 9.
Let Q be the intersection of the terminal ray with the unit circle after being rotated by π – θ radians.
a. What is the slope of ![]() ?
?
Answer:
Ray ![]() is the reflection of ray
is the reflection of ray ![]() across the y-axis, so the coordinates of Q are (- x0, yo). Then, the slope of
across the y-axis, so the coordinates of Q are (- x0, yo). Then, the slope of ![]() is the opposite of the slope of
is the opposite of the slope of ![]() so the slope of
so the slope of ![]() is – m.
is – m.
b. Find an expression for tan(π – θ) in terms of m.
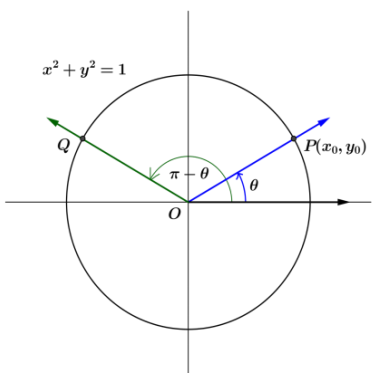
Answer:
tan(π – θ) – m
c. Find an expression for tan(π – θ) in terms of tan(θ).
Answer:
tan(π – θ) = – tan(θ)
Exercise 10.
Let Q be the intersection of the terminal ray with the unit circle after being rotated by \(\frac{\pi}{2}\) + θ radians.
a. What is the slope of ![]() ?
?
Answer:
Ray ![]() is the rotation of
is the rotation of ![]() by 90° counterclockwise, so line OQ is perpendicular to
by 90° counterclockwise, so line OQ is perpendicular to ![]() Thus, the slopes of
Thus, the slopes of ![]() and
and ![]() are opposite reciprocals. Thus, the slope of
are opposite reciprocals. Thus, the slope of ![]() is –\(\frac{1}{m}\).
is –\(\frac{1}{m}\).
b. Find an expression for tan (\(\frac{\pi}{2}\) + θ) in terms of m.
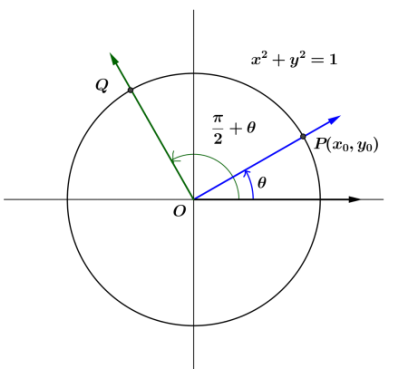
Answer:
tan(\(\frac{\pi}{2}\) + θ) = –\(\frac{1}{m}\)
c. Find an expression for tan (\(\frac{\pi}{2}\) + θ) first in terms of tan(θ) and then in terms of cot(θ).
Answer:
tan(\(\frac{\pi}{2}\) + θ) = –\(\frac{1}{\tan (\theta)}\) = -cot(θ)
Exercise 11.
Let Q be the intersection of the terminal ray with the unit circle after being rotated by \(\frac{\pi}{2}\) – θ radians.
a. What is the slope of ![]() ?
?
Answer:
Ray OQI s the reflection of ![]() across the diagonal line y = x, so the coordinates of Q are (yo, x0).
across the diagonal line y = x, so the coordinates of Q are (yo, x0).
Then, the slope of ![]() is –\(\frac{1}{m}\).
is –\(\frac{1}{m}\).
b. Find an expression for tan (\(\frac{\pi}{2}\) – θ) in terms of m.
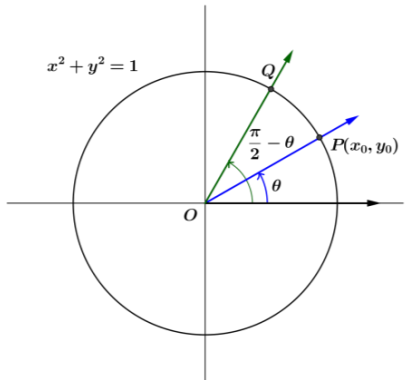
Answer:
tan(\(\frac{\pi}{2}\) – θ) = –\(\frac{1}{m}\)
c. Find an expression for tan (\(\frac{\pi}{2}\) – θ) first in terms of tan(θ) and then in terms of cot(θ).
Answer:
tan(\(\frac{\pi}{2}\) – θ) = –\(\frac{1}{\tan (\theta)}\) = cot(θ)
Exercise 12.
Summarize your results from Exercises 6, 7, 9, 10 and 11.
Answer:
For 0 < θ < \(\frac{\pi}{2}\):
tan (θ + π) = tan (θ)
tan (-θ) = -tan (θ)
tan (π – θ) = -tan (θ)
tan (\(\frac{\pi}{2}\) + θ) = –\(\frac{1}{\tan (\theta)}\)
tan (\(\frac{\pi}{2}\) – θ) = \(\frac{1}{\tan (\theta)}\)
Exercise 13.
We have only demonstrated that the identities in Exercise 12 are valid for 0 < θ < \(\frac{\pi}{2}\) because we only used rotations that left point P in the first quadrant. Argue that tan (-\(\frac{2 \pi}{3}\)) = -tan (\(\frac{2 \pi}{3}\)). Then, using similar logic, we could argue that all of the above identities extend to any value of θ for which the tangent (and cotangent for the
last two) is defined.
Answer:
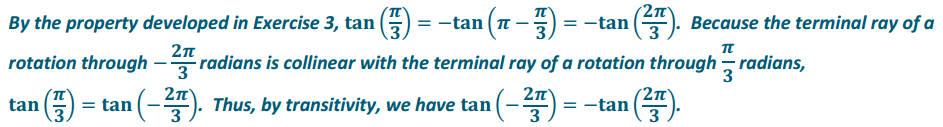
Exercise 14.
For which values of θ are the identities in Exercise 12 valid?
Answer:
Using a process similar to the one we used in Exercise 13, we can show that the value of θ can be any real number that does not cause a zero in the denominator. The tangent function ¡s only defined for θ ≠ \(\frac{\pi}{2}\) + πk, for all integers k. Also, for those identities involving cot(θ), we need to have θ ≠ πk, for all integers k.
Exercise 15.
Derive an identity for tan(2π + θ) from the graph.
Answer:
Because the terminal ray for a rotation by 2π + θ and the terminal ray for a rotation by θ coincide, we see that tan(2π + θ) = tan(θ), where θ ≠ \(\frac{\pi}{2}\) + kπ, for all integers k.
Exercise 16.
Use the identities you summarized in Exercise 12 to show tan(2π – θ) = – tan(θ) where θ ≠ \(\frac{\pi}{2}\) + kπ, for all integers k.
Answer:
From Exercise 6, tan(2π – θ) = tan(π + (π – θ)) = tan(π – θ) = tan(-θ).
From Exercise 7, tan(-θ) = -tan(θ).
Thus, tan(2π – θ) = -tan(θ) for θ ≠ \(\frac{\pi}{2}\) + kπ, for all integers k.
Eureka Math Algebra 2 Module 2 Lesson 14 Problem Set Answer Key
Question 1.
Recall that the cotangent function is defined by cot(x) = \(\frac{\cos (x)}{\sin (x)}=\frac{1}{\tan (x)}\), where sin(x) ≠ 0.
a. What is the domain of the cotangent function? Explain how you know.
Answer:
Since the cotangent function is given by cot(x) = \(\frac{\cos (x)}{\sin (x)}\) the cotangent function is undefined at values of x, where sin(x) = 0. This happens at values of θ that are multiples of π.
b. What is the period of the cotangent function? Explain how you know.
Answer:
Since the cotangent function ¡s the reciprocal of the tangent function, they will have the same period, π. That is, cot(x + π) = \(\frac{1}{\tan (x+\pi)}=\frac{1}{\tan (x)}\) = cot(x).
c. Use a calculator to complete the table of values of the cotangent function on the interval (0, π) to two decimal places.
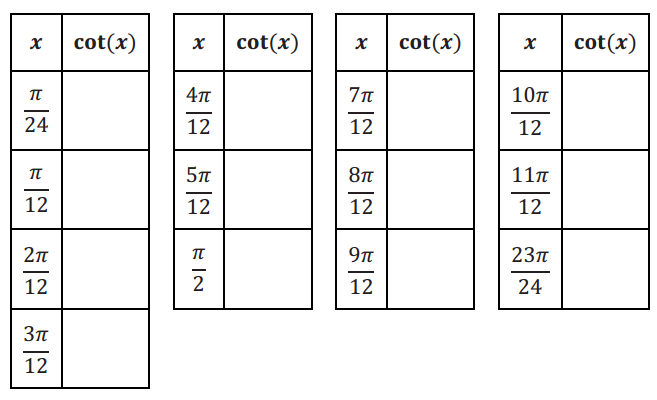
Answer:
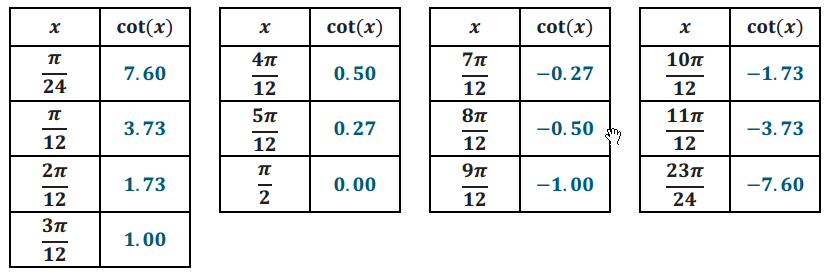
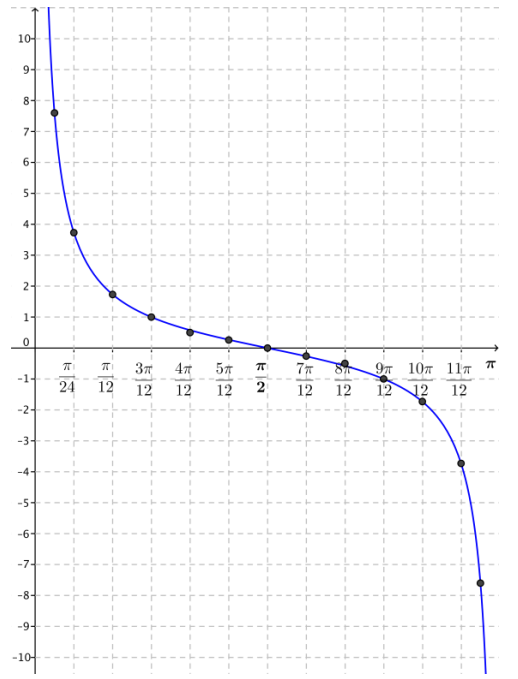
d. Plot your data from part (c), and sketch a graph of y = cot(x) on (0, π).
Answer:
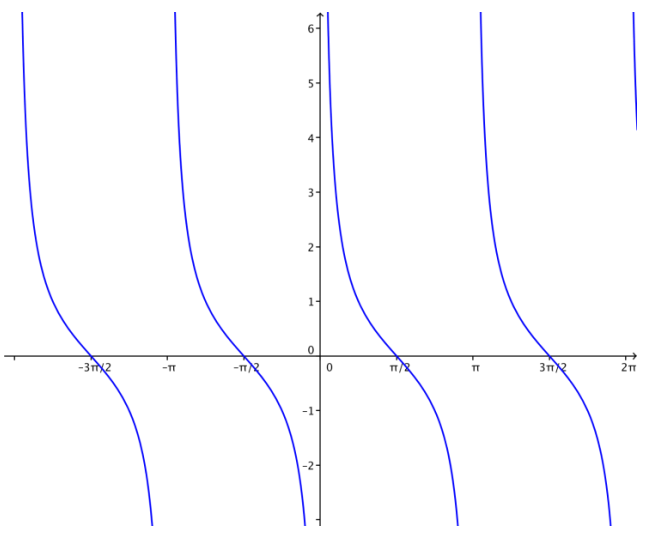
e. Sketch a graph of y = cot(x) on (-2π, 2π) without plotting points.
Answer:
f. Discuss the similarities and differences between the graphs of the tangent and cotangent functions.
Answer:
Both the tangent and cotangent functions have vertical asymptotes; the cotangent graph has vertical asymptotes at x = kπ, for integers k, and the tangent has vertical asymptotes at x = \(\frac{\pi}{2}\) + kπ, for integers k. The values of the tangent function increase as we look at each piece of the graph from left to right, and the values of the cotangent function decrease as we look at each piece from left to right.
g. Find all x-values where tan(x) = cot(x) on the interval (0, 2π).
Answer:
Suppose that tan(x) = cot(x). Then, \(\frac{\sin (x)}{\cos (x)}=\frac{\cos (x)}{\sin (x)}\).
Cross multiplying gives
(sin(x))2 = (cos(x))2
(sin(x))2 – (cos(x))2 = 0
(sin(x) – cos(x)) (sin(x) + cos(x)) = 0
sin(x) = cos(x) or sin(x) = – cos(x).
The solutions are \(\frac{\pi}{4}\), \(\frac{3\pi}{4}\), \(\frac{5\pi}{4}\), and \(\frac{7\pi}{4}\). These are the x-values of the points of intersection of the graphs of the two functions shown to the right.
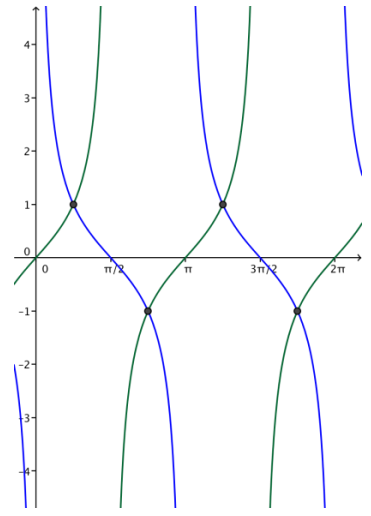
Question 2.
Each set of axes below shows the graph of f(x) = tan(x). Use what you know about function transformations to sketch a graph of y = g(x) for each function g on the interval (0, 2π).
a. g(x) = 2tan(x)
Answer:
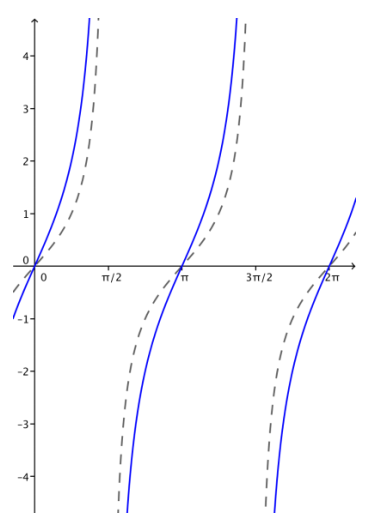
b. g(x) = \(\frac{1}{3}\)tan(x)
Answer:

c. g(x) = – 2 tan(x)
Answer:
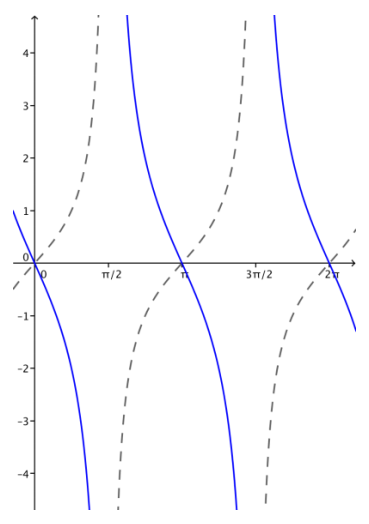
d. How does changing the parameter A affect the graph of g(x) = A tan(x)?
Answer:
If A is positive, the graph is scaled vertically by a factor of A. If A is negative, then the graph is reflected over the x-axis and scaled vertically by a factor of |A|.
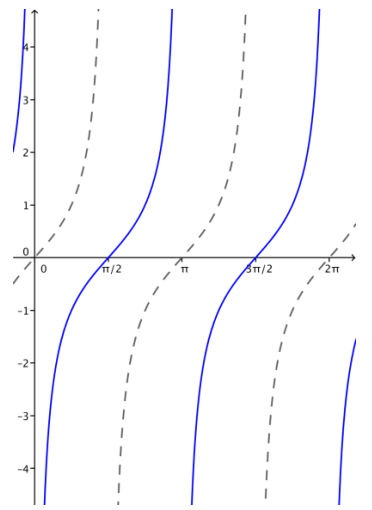
Question 3.
Each set of axes below shows the graph of f(x) = tan(x). Use what you know about function transformations to sketch a graph of y = g(x) for each function g on the interval (0, 2π).
a. g(x) = tan(x – \(\frac{\pi}{2}\))
Answer:
b. g(x) = tan (x – \(\frac{\pi}{6}\))
Answer:
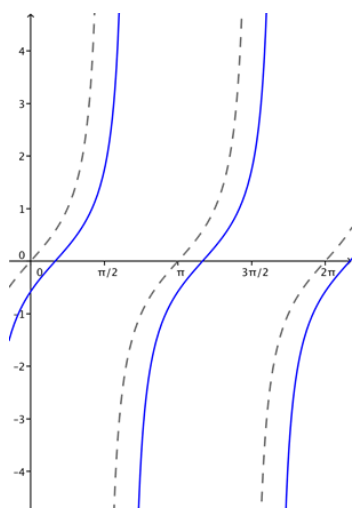
c. g(x) = tan (x + \(\frac{\pi}{4}\))
Answer:

d. How does changing the parameter h affect the graph of g(x) = tan(x – h)?
Answer:
If h > 0, the graph is translated horizontally to the right by h units, and if h < 0, the graph is translated horizontally to the left by h units.
Question 4.
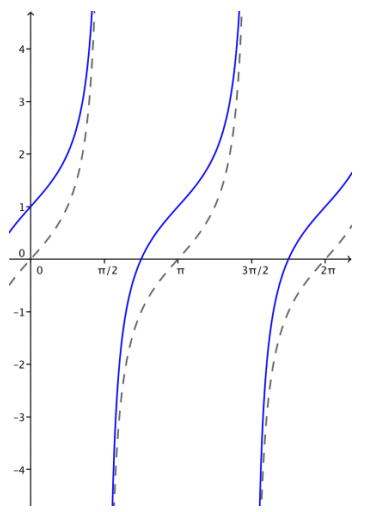
Each set of axes below shows the graph of f(x) = tan(x). Use what you know about function transformations to sketch a graph of y = g(x) for each function g on the interval (O, 2ir). a. g(x) = tan(x) + 1
Answer:
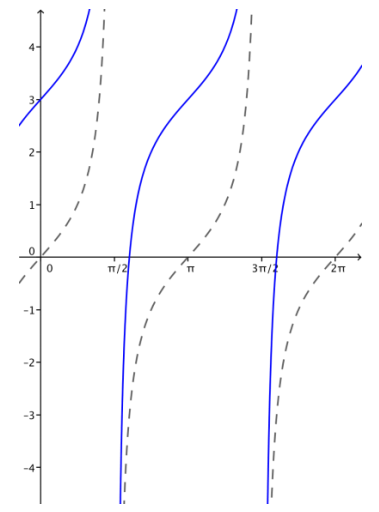
b. g(x) = tan(x) + 3
Answer:
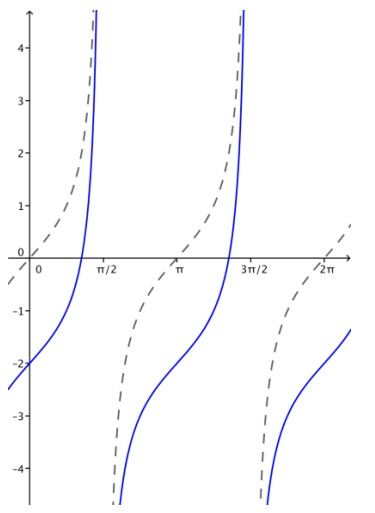
c. g(x) = tan(x) – 2
Answer:
d. How does changing the parameter k affect the graph of g(x) = tan(x) + k? Answer: If k > 0, the graph is translated vertically upward by k units, and if k < 0, the graph is translated vertically downward by k units.
Question 5.
Each set of axes below shows the graph of f(x) = tan(x). Use what you know about function transformations to sketch a graph of y = g(x) for each function g on the interval (0, 2π).
a. g(x) = tan(3x)
Answer:
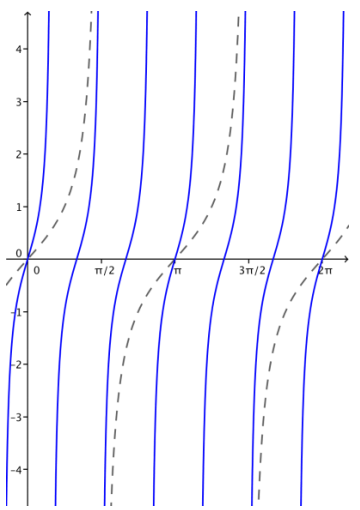
b. g(x) = tan\(\left(\frac{x}{2}\right)\)
Answer:

c. g(x) = tan(-3x)
Answer:
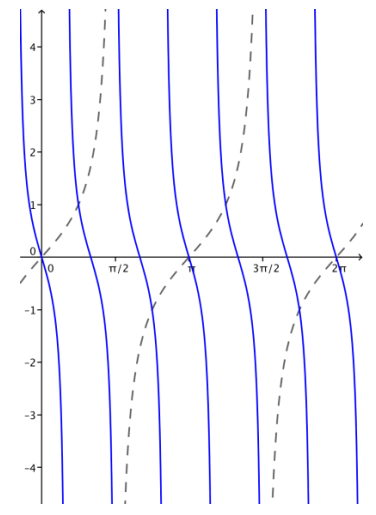
d. How does changing the parameter ¿û affect the graph of g(x) = tan(ωx)?
Answer:
Changing ω changes the period of the graph. The period is P = \(\frac{\pi}{|\omega|}\)
Question 6.
Use your knowledge of function transformation and the graph of y = tan(x) to sketch graphs of the following transformations of the tangent function.
a. y = tan(2x)
Answer:
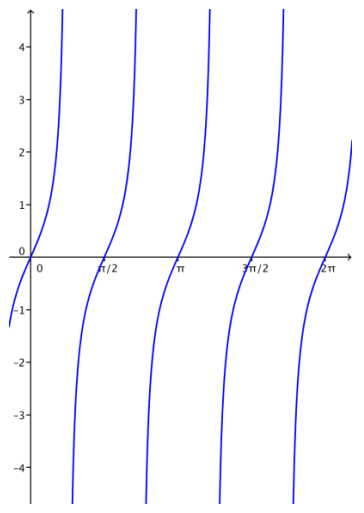
b. y = tan(2 (x – \(\frac{\pi}{4}\)))
Answer:
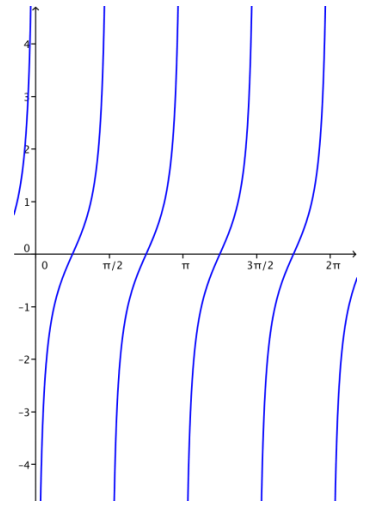
c. y = tan(2 (x – \(\frac{\pi}{4}\))) + 1.5
Answer:

Question 7.
Find parameters A, ω, h, and k so that the graphs of f(x) = A tan(ω(x – h)) + k and g(x) = cot(x) are the
same.
The graphs of f(x) = – tan (x – \(\frac{\pi}{2}\)) and g(x) = cot(x) are the same graph.
Eureka Math Algebra 2 Module 2 Lesson 14 Exit Ticket Answer Key
Question 1.
Sketch a graph of the function f(x) = tan(x), marking the important features of the graph.
Answer:
Students should mark the period, the 1800 rotational symmetry, and the vertical asymptotes where the function is undefined.
Question 2.
Given tan(x) = 7, find the following function values:
a. tan(π + x)
Answer:
tan(π + x) = tan(x) = 7
b. tan(2π – x)
Answer:
tan(2π – x) = tan(π – x) = – tan(x) = – 7
c. tan(\(\frac{\pi}{2}\) + x)
Answer:
tan(\(\frac{\pi}{2}\) + x) = – cot(x) = –\(\frac{1}{\tan (x)}=-\frac{1}{7}\)