Engage NY Eureka Math Algebra 2 Module 1 Lesson 38 Answer Key
Eureka Math Algebra 2 Module 1 Lesson 38 Example Answer Key
Example 1.
Consider the equation 3x + x2 = – 7.
What does the value of the discriminant tell us about number of solutIons to this equation?
Solve the equation. Does the number of solutions match the Information provided by the discriminant? Explain.
Answer:
Consider the equation 3x + x2 = – 7.
→ What does the value of the discriminant tell us about number of solutions to this equation?
The equation in standard form is x2 + 3x + 7 = 0, so we have a = 1, b = 3, c = 7.
The discriminant is 32 – 4(1)(7) = – 19. The negative discriminant indicates that no real solutions exist. There are two complex solutions.
→ Solve the equation. Does the number of solutions match the information provided by the discriminant? Explain.
Using the quadratic formula,
x = \(\frac{-3+\sqrt{-19}}{2}\) or x = \(\frac{-3+\sqrt{-19}}{2}\)
The solutions, in a + bi form, are \(-\frac{3}{2}+\frac{\sqrt{19}}{2} i\) and \(-\frac{3}{2}-\frac{\sqrt{19}}{2} i\).
The two complex solutions are consistent with the rule for a negative discriminant.
Eureka Math Algebra 2 Module 1 Lesson 38 Opening Exercise Answer Key
Exercise 1.
The expression under the radical in the quadratic formula, b2 – 4ac, is called the discriminant.
Use the quadratic formula to solve the following quadratic equations. Calculate the discriminant for each equation.
a. x2 – 9 = 0
Answer:
The equation x2 – 9 = 0 has two real solutions: x = 3 and x = – 3. The discriminant of x2 – 9 = 0 is 36.
b. x2 – 6x + 9 = 0
Answer:
The equation x2 – 6x + 9 = 0 has one real solution: x = 3. The discriminant of x2 – 6x + 9 = 0 is 0.
c. x2 + 9 = 0
Answer:
The equation x2 + 9 = 0 has two complex solutions: x = 3i and x = – 3i. The discriminant of x2 + 9 = 0 is – 36.
Exercise 2.
How does the value of the discriminant for each equation relate the number of solutions you found?
Answer:
If the discriminant is negative, the equation has complex solutions. If the discriminant is zero, the equation has one real solution. If the discriminant is positive. the equation has two real solutions.
Eureka Math Algebra 2 Module 1 Lesson 38 Exercise Answer Key
Exercise
Compute the value of the discriminant of the quadratic equation In each part. Use the value of the discriminant to predict the number and type of solutions. Find all real and complex solutions.
a. x2 + 2x + 1 = 0
Answer:
We have a = 1, b = 2, and c = 1. Then
b2 – 4ac = 22 – 4(1)(1) = 0.
Note that the discriminant Is zero, so this equation has exactly one real solution.
x = \(\frac{-(2) \pm \sqrt{0}}{2(1)}\) = – 1
Thus, the only solution is – 1.
b. x2 + 4 = 0
Answer:
We have a = 1, b = 0, and c = 4. Then
b2 – 4ac = – 16.
Note that the discriminant is negative, so this equation has two complex solutions.
x = \(\frac{-0 \pm \sqrt{-16}}{2(1)}\)
Thus, the two complex solutions are 2i and – 2i.
c. 9x2 – 4x – 14 = 0
Answer:
We have a = 9, b = – 4, and c = – 14. Then
b2 – 4ac = (-4)2 – 4(9)(- 14)
= 16 + 504
= 520.
Note that the discriminant is positive, so this equation has two distinct real solutions.
Using the quadratic formula,
x = \(\frac{-(-4) \pm 2 \sqrt{130}}{2(9)}\)
So, the two real solutions are \(\frac{2+\sqrt{130}}{9}\) and \(\frac{2-\sqrt{130}}{9}\).
d. 3x2 + 4x + 2 = 0
Answer:
We have a = 3, b = 4, and c = 2. Then
b2 – 4ac = 42 – 4(3)(2)
= 16 – 24
= – 8.
The discriminant is negative, so there will be two complex solutions. Using the quadratic formula,
x = \(\frac{-4 \pm \sqrt{-8}}{2(3)}\)
So, the two complex solutions are \(-\frac{2}{3}+\frac{\sqrt{2}}{3} i\) and \(-\frac{2}{3}-\frac{\sqrt{2}}{3} i\).
e. x = 2x2 + 5
Answer:
We can rewrite this equation in standard form with a = 2, b = – 1, and c = 5:
2x2 – x + 5 = 0.
Then
b2 – 4ac = (-1)2 – 4(2)(5)
= 1 – 40
= – 39.
The discriminant is negative, so there will be two complex solutions. Using the quadratic formula,
x = \(\frac{-(-1) \pm \sqrt{-39}}{2(2)}\)
x = \(\frac{1 \pm i \sqrt{39}}{4}\)
The two solutions are \(\frac{1}{4}+\frac{\sqrt{39}}{4} i\) and \(\frac{1}{4}-\frac{\sqrt{39}}{4} i\).
f. 8x2 + 4x + 32 = 0
Answer:
We can factor 4 from the left side of this equation to obtain 4(2x2 + x +8) = 0, and we know that a product is zero when one of the factors are zero. Since 4 ≠ 0, we must have 2x2 + x + 8 = 0. This is a quadratic equation with a = 2, b = 1, and
c = 8. Then
b2 – 4ac = 12 – 4(2)(8) = – 63.
The discriminant is negative, so there will be two complex solutions. Using the quadratic formula,
x = \(\frac{-1 \pm \sqrt{-63}}{2(2)}\)
x = \(\frac{-1 \pm 3 i \sqrt{7}}{4}\)
The complex solutions are \(-\frac{1}{4}+\frac{3 \sqrt{7}}{4} i\) and \(-\frac{1}{4}-\frac{3 \sqrt{7}}{4} i\).
Eureka Math Algebra 2 Module 1 Lesson 38 Problem Set Answer Key
Question 1.
Give an example of a quadratic equation in standard form that has …
a. Exactly two distinct real solutions.
Answer:
Since (x + 1)(x – 1) = – 1, the equation x2 – 1 = 0 has two distinct real solutions, 1 and – 1.
b. Exactly one distinct real solution.
Answer:
Since (x + 1)2 = x2 + 2x + 1, the equation x2 + 2x + 1 = 0 has only one real solution, 1.
c. Exactly two complex (non-real) solutions.
Answer:
Since x2 + 1 = 0 has no solutions in the real numbers, this equation must have two complex solutions. They are i and -i.
Question 2.
Suppose we have a quadratic equation ax2 + bx + c = 0 so that a + c = 0. Does the quadratic equation have one solution or two distinct solutions? Are they real or complex? Explain how you know.
Answer:
If a + c = 0, the neither a = c = 0, a > 0 and c < 0, or a < 0 and c > 0.
The definition of a quadratic polynomial requires that a ≠ 0, so either a > 0 and c < 0 or a < 0 and c > 0.
In either case, 4ac < 0. Because b2 is positive and 4ac is negative, we know b2 – 4ac > 0.
Therefore, a quadratic equation ax2 + bx + c = 0 always has two distinct real solutions when a + c = 0.
Question 3.
Solve the equation 5x2 – 4x + 3 = 0.
Answer:
We have a quadratic equation with a = 5, b = – 4, and c = 3.
x = \(\frac{-(-4) \pm 2 \sqrt{-11}}{2(5)}\)
So, the solutions are \(\) and \(\frac{2}{5}-\frac{i \sqrt{11}}{5}\) .
Question 4.
Solve the equation 2x2 + 8x = – 9.
Answer:
In standard form, this is the quadratic equation 2x2 + 8x + 9 = 0 with a = 2, b = 8, and c = 9.
x = \(\frac{-8 \pm 2 \sqrt{-2}}{2(2)}\) = \(\frac{-4 \pm i \sqrt{2}}{2}\)
Thus, the solutions are 2 + \(\frac{i \sqrt{2}}{2}\) and 2 – \(\frac{i \sqrt{2}}{2}\)
Question 5.
Solve the equation 9x – 9x2 = 3 + x + x2.
Answer:
In standard form, this is the quadratic equation 10x2 – 8x + 3 = 0 with a = 10, b = – 8, and c = 3.
x = \(\frac{-(-8) \pm 2 \sqrt{-14}}{2(10)}\) = \(\frac{8 \pm 2 i \sqrt{14}}{20}\)
Thus, the solutions are \(\frac{2}{5}+\frac{i \sqrt{14}}{10}\) and \(\frac{2}{5}-\frac{i \sqrt{14}}{10}\).
Question 6.
Solve the equation 3x2 – x + 1 = 0.
Answer:
This is a quadratic equation with a = 3, b = – 1, and c = 1.
x = \(\frac{-(-1) \pm \sqrt{-11}}{2(3)}\) = \(\frac{1 \pm i \sqrt{11}}{6}\)
Thus, the solutions are \(\frac{1}{6}+\frac{i \sqrt{11}}{6}\) and \(\frac{1}{6}-\frac{i \sqrt{11}}{6}\)
Question 7.
Solve the equation 6x4 + 4x2 – 3x + 2 = 2x2(3x2 – 1).
Answer:
When expanded, this is a quadratic equation with a = 6, b = – 3, and c = 2.
6x4 + 4x2 – 3x + 2 = 6x4 – 2x2
6x2 – 3x + 2 = 0
x = \(\frac{-(-3) \pm \sqrt{\{-39\}}}{2(6)}\)
So, the solutions are \(\frac{1}{4}+\frac{i \sqrt{39}}{12}\) and \(\frac{1}{4}-\frac{i \sqrt{39}}{12}\)
Question 8.
Solve the equation 25x2 + 100x + 200 = 0.
Answer:
We can factor 25 from the left side of this equation to obtain 25 (x2 + 4x + 8) = 0, and we know that a product is zero when one of the factors is zero. Since 25 ≠ 0, we must have x2 + 4x + 8 = 0. This is a quadratic equation with a = 1, b = 4, and c = 8. Then
x = \(\frac{-4 \pm 4 \sqrt{-1}}{2}\)
and the solutions are – 2 + 2i and – 2 – 2i.
Question 9.
Write a quadratic equation in standard form such that – 5 is its only solution.
Answer:
(x + 5)2 = 0
x2 + 10x + 25 = 0
Question 10.
Is it possible that the quadratic equation ax2 + bx + c = 0 has a positive real solution if a, b, and c are all positive real numbers?
Answer:
No. The solutions are \(\frac{-b+\sqrt{b^{2}-4 a c}}{2 a}\) and \(\frac{-b-\sqrt{b^{2}-4 a c}}{2 a}\). If b is positive, the second one of these will be negative. So, we need to think about whether or not the first one can be positive. If – b + \(\sqrt{b^{2}-4 a c}\) > 0, then \(\sqrt{b^{2}-4 a c}\) > b; so, b2 – 4ac > b2, and – 4ac > 0. This means that either a or c must be negative. So, if all three coefficients are positive, then there cannot be a positive solution to ax2 + bx + c = 0.
Question 11.
Is it possible that the quadratic equation ax2 + bx + c = 0 has a positive real solution if a, b, and c are all negative real numbers?
Answer:
No. If a, b, and c are all negative, then – a, – b, and – c are all positive. The solutions of ax2 + bx + c = 0 are the same as the solutions to – ax2 – bx – c = 0, and by Problem 10, this equation has no positive real solution since it has all positive coefficients.
Extension:
Question 12.
Show that if k > 3.2, the solutions of 5x2 – 8x + k = 0 are not real numbers.
Answer:
We have a = 5, b = – 8, and c = k; then
b2 – 4ac = (-8)2 – 45k
= 64 – 20k.
When the discriminant is negative, the solutions of the quadratic function are not real numbers.
b2 – 4ac = 64 – 20k
k < 3.2
b2 -4ac < 64 – 20(3.2)
b2 – 4ac < 0 k >3.2
Thus, if k > 3.2, then the discriminant is negative and the solutions of 5x2 – 8x + k = 0 are not real numbers.
Question 13.
Let k be a real number, and consider the quadratic equation (k + 1)x2 + 4kx + 2 = 0.
a. Show that the discriminant of (k + 1)x2 + 4kx + 2 = 0 defines a quadratic function of k.
Answer:
The discriminant of a quadratic equation written in the form ax2 + bx + c = 0 is b2 – 4ac.
Here, a = k + 1, b = 4k, and c = 2. We get
b2– 4ac = (4k)2 – 4 ∙ (k + 1) ∙ 2
= 16k2 – 8(k+ 1)
= 16k2 – 8k – 8.
With k unknown, we can write f(k) = 16k2 – 8k – 8, which is a quadratic function of k.
b. Find the zeros of the function in part (a), and make a sketch of its graph.
Answer:
If f(k) = 0, then we have
0 = 16k2 – 8k – 8
= 2k2 – k – 1
= 2k2 – 2k + k – 1
= 2k(k – 1) + 1 (k – 1)
= (k – 1) (2k + 1).
Then, k – 1 = 0 or 2k+ 1 = 0.
So, k = 1 or k = –\(\frac{1}{2}\).
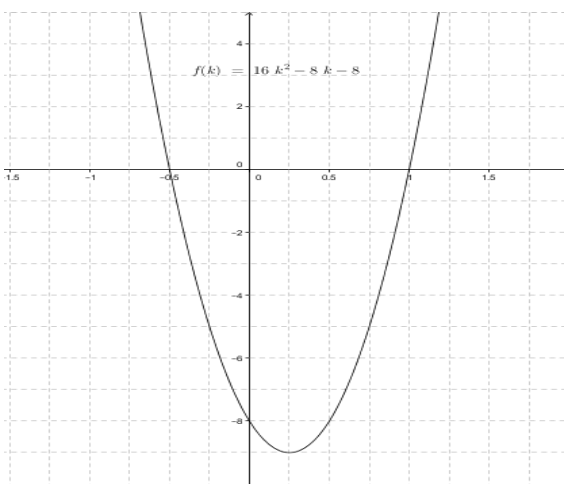
c. For what value of k are there two distinct real solutions to the original quadratic equation?
Answer:
The original quadratic equation has two distinct real solutions when the discriminant given by f(k) is positive. This occurs for all real numbers k such that k < –\(\frac{1}{2}\) or k > 1.
d. For what value of k are there two complex solutions to the given quadratic equation?
Answer:
There are two complex solutions when f(k) < 0. This occurs for all real numbers k such that – \(\frac{1}{2}\) < k < 1.
e. For what value of k is there one solution to the given quadratic equation?
Answer:
There is one solution when f(k) = 0. This occurs at k = –\(\frac{1}{2}\) and k = 1.
Question 14.
We can develop two formulas that can help us find errors in calculated solutions of quadratic equations.
a. Find a formula for the sum S of the solutions of the quadratic equation ax2 + bx + c = 0.
Answer:
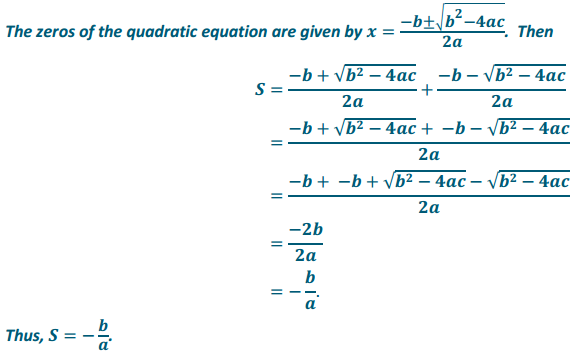
b. Find a formula for the product R of the solutions of the quadratic equation ax2 + bx + c = 0.
Answer:
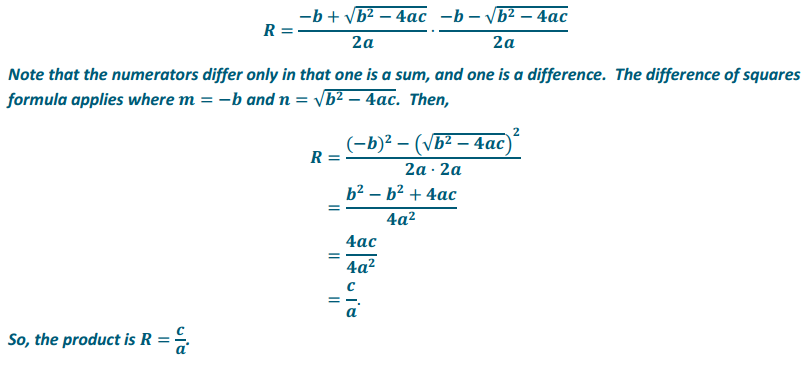
c. June calculated the solutions 7 and – 1 to the quadratic equation x2 – 6x + 7 = 0. Do the formulas from parts (a) and (b) detect an error in her solutions? If not, determine if her solution is correct.
Answer:
The sum formula agrees with June’s calculations. From June’s zeros,
7 + – 1 = 6,
and from the formula,
S = \(\frac{6}{1}\) = 6.
However, the product formula does not agree with her calculations. From June’s zeros,
7 ∙ – 1 – 7,
and from the formula,
R = \(\frac{7}{1}\) = 7.
June’s solutions are not correct: (7)2 – 6(7) + 7 = 49 – 42 + 7 = 14; so, 7 is not a solution to this quadratic equation. Likewise, 1 – 6 + 7 = 2, so 1 is also not a solution to this equation. Thus, the formulas caught her error.
d. Paul calculated the solutions 3 – i√2 and 3 + i√2 to the quadratic equation x2 – 6x + 7 = 0. Do the formulas from parts (a) and (b) detect an error in his solutions? If not, determine if his solutions are correct.
Answer:
In part (c), we calculated that R = 7 and S = 6. From Paul’s zeros,
S = 3 + i√2 + 3 – i√2 = 6,
and for the product,
R = (3 + i√2) ∙ (3 – i√2)
= 32 – (i√2)2
= 9 – 1 ∙ 2
= 11.
This disagrees with the calculated version of R. So, the formulas do find that he made an error.
e. Joy calculated the solutions 3 – √2 and 3 + √2 to the quadratic equation x2 – 6x + 7 = 0. Do the formulas from parts (a) and (b) detect an error in her solutions? If not, determine if her solutions are correct.
Answer:
Joy’s zeros will have the same sum as Paul’s, so S = 6, which agrees with the sum from the formula. For the product of her zeros we get
R = (3 – √2) (3 + √2)
= 9 – 2
= 7,
which agrees with the formulas.
Checking her solutions in the original equation, we find
(3 – √2)2 – 6(3 – √2) + 7 = (9 – 6√2 + 2) – 18 + 6√2 + 7 = 0,
(3 + √2)2 – 6(3 – √2) + 7 = (9 + 6√2 + 2) – 18 + 6√2 + 7 = 0.
Thus, Joy has correctly found the solutions of this quadratic equation.
f. If you find solutions to a quadratic equation that match the results from parts (a) and (b), does that mean your solutions are correct?
Answer:
Not necessarily. We only know that if the sum and product of the solutions do not match S and R, then we have not found a solution. Evidence suggests that if the sum and product of the solutions do match S and R, then we have found the correct solutions, but we do not know for sure until we check.
g. Summarize the results of this exercise.
Answer:
For a quadratic equation of the form ax2 + bx + c = 0, the sum of the solutions is given by S = –\(\frac{b}{a}\) and the product of the solutions is given by R = \(\frac{c}{a}\) . So, multiplying and adding the calculated solutions will identify if we have made an error. Passing these checks, however, does not guarantee that the numbers we found are the correct solutions.
Eureka Math Algebra 2 Module 1 Lesson 38 Exit Ticket Answer Key
Use the discriminant to predict the nature of the solutions to the equation 4x – 3x2 = 10. Then, solve the equation.
Answer:
3x2 – 4x + 10 = 0
We have a = 3, b = -4, and c= 10. Then
b2 – 4ac = (-4)2 – 4(3)(10)
= 16 – 120
= – 104.
The value of the discriminant is negative, indicating that there are two complex solutions.
x = \(\frac{-(-4) \pm \sqrt{-104}}{2(3)}\)
x = \(\frac{4 \pm 2 i \sqrt{26}}{6}\)
Thus, the two solutions are \(\frac{2}{3}+\frac{\sqrt{26}}{3} i\) and \(\frac{2}{3}-\frac{\sqrt{26}}{3} i\).