Engage NY Eureka Math Algebra 2 Module 1 Lesson 26 Answer Key
Eureka Math Algebra 2 Module 1 Lesson 26 Example Answer Key
Example 1.
Solve the following equation: \(\frac{x+3}{12}=\frac{5}{6}\).
Answer:
Equating Numerators Method: Obtain expressions on both sides with the same denominator and equate numerators.

Thus, x + 3 = 10, and x = 7; therefore, 7 is the solution to our original equation.
Clearing Fractions Method: Multiply both sides by a common multiple of the denominators to clear the fractions, and then solve the resulting equation.
\(12 \cdot\left(\frac{x+3}{12}\right)=12 \cdot\left(\frac{5}{6}\right)\)
x + 3 = 10
We can see, once again, that the solution is 7.
Eureka Math Algebra 2 Module 1 Lesson 26 Exercise Answer Key
Solve the following equations for x, and give evidence that your solutions are correct.
Exercise 1.
\(\frac{x}{2}+\frac{1}{3}=\frac{5}{6}\)
Answer:

Exercise 2.
\(\frac{2 x}{9}+\frac{5}{9}=\frac{8}{9}\)
Answer:
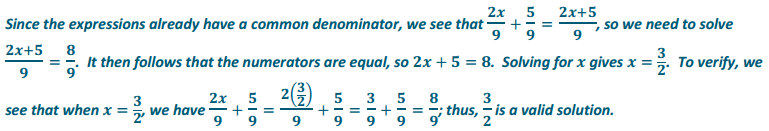
Exercise 3.
Solve the following equation: \(\frac{3}{x}=\frac{8}{x-2}\).
Answer:
Method 1: Convert both expressions to equivalent expressions with a common denominator. The common denominator is x(x – 2), so we use the identity property of multiplication to multiply the left side by \(\frac{x-2}{x-2}\) and the right side by \(\frac{x}{x}\). This does not change the value of the expression on either side of the equation.
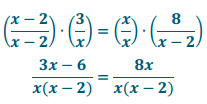
Since the denominators are equal, we can see that the numerators must be equal; thus, 3x – 6 = 8x. Solving for x gives a solution of –\(\frac{6}{5}\). At the outset of this example, we noted that x cannot take on the value of 0 or 2, but there is nothing preventing x from taking on the value –\(\frac{6}{5}\). Thus, we have found a solution. We can check our work. Substituting –\(\frac{6}{5}\) into \(\frac{3}{x}\) gives us \(\frac{3}{(-6 / 5)}\) = –\(\frac{5}{2}\) and substituting –\(\frac{6}{5}\) into \(\frac{8}{x-2}\) gives us \(\frac{8}{(-6 / 5)-2}\) = –\(\frac{5}{2}\). Thus, when x = –\(\frac{6}{5}\), we have \(\frac{3}{x}\) = \(\frac{8}{x – 2}\); therefore, –\(\frac{6}{5}\) is indeed a solution.
Method 2: Multiply both sides of the equation by the common denominator x(x – 2), and solve the resulting equation.
x(x – 2) \(\left(\frac{3}{x}\right)\) = x(x – 2) \(\left(\frac{8}{x-2}\right)\)
3(x – 2) = 8x
3x – 6 = 8x
From this point, we follow the same steps as we did in Method 1, and we get the same solution: –\(\frac{6}{5}\)
Exercise 4.
Solve the following equation for a: \(\frac{1}{a+2}+\frac{1}{a-2}=\frac{4}{a^{2}-4}\)
Answer:
First, we notice that we must have a ≠ 2 and a ≠ – 2. Then, we apply Method 1:
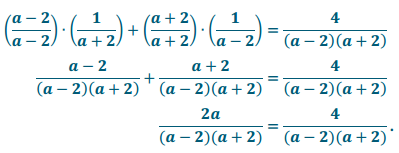
Since the denominators are equal, we know that the numerators are equal; thus, we have 2a = 4, which means that a = 2. Thus, the only solution to this equation is 2. However, a is not allowed to be 2 because if a = 2, then \(\frac{1}{a-2}\) is not defined. This means that the original equation, \(\frac{1}{a+2}+\frac{1}{a-2}=\frac{4}{a^{2}-4}\), has no solution.
Exercise 5.
Solve the following equation. Remember to check for extraneous solutions.
\(\frac{4}{3 x}+\frac{5}{4}=\frac{3}{x}\)
Answer:
First, note that we must have x ≠ 0.
Equating numerators: \(\frac{16}{12 x}+\frac{15 x}{12 x}=\frac{36}{12 x}\)
Then, we have 16 + 15x = 36, and the solution is x = \(\frac{4}{3}\).
Clearing fractions: \(12 x\left(\frac{4}{3 x}+\frac{5}{4}\right)=12 x\left(\frac{3}{x}\right)\)
Then, we have 16 + 15x = 36, and the solution is x = \(\frac{4}{3}\)
The solution \(\frac{4}{3}\) is valid since the only excluded value is 0.
Exercise 6.
Solve the following equation. Remember to check for extraneous solutions.
\(\frac{7}{b+3}+\frac{5}{b-3}=\frac{10 b-2}{b^{2}-9}\)
Answer:
First, note that we must have x ≠ 3 and x ≠ – 3.
Equating numerators: \(\frac{7(b-3)}{(b-3)(b+3)}\) + \(\frac{5(b+3)}{(b-3)(b+3)}\) = \(\frac{10 b-2}{(b-3)(b+3)}\)
Matching numerators, we hove 7b – 21 + 5b + 15 = 10b – 2, which leads to 2b = 4; therefore, b = 2.
Clearing fractions: (b – 3)(b + 3) \(\left(\frac{7}{b+3}+\frac{5}{b-3}\right)\) = (b – 3)(b + 3) \(\left(\frac{10 b-2}{b^{2}-9}\right)\)
We have 7(b – 3) + 5(b + 3) = 10b – 2, which leads to 2b = 4; therefore, b = 2.
The solution 2 is valid since the only excluded values are 3 and – 3.
Exercise 7.
Solve the following equation. Remember to check for extraneous solutions.
\(\frac{1}{x-6}+\frac{x}{x-2}=\frac{4}{x^{2}-8 x+12}\)
Answer:
First, note that we must have x ≠ 6 and x ≠ 2.
Equating numerators:
\(\frac{x-2}{(x-6)(x-2)}\) + \(\frac{x^{2}-6 x}{(x-6)(x-2)}\) = \(\frac{4}{(x-6)(x-2)}\)
x2 – 5x – 2 = 4
x2 – 5x – 6 = 0
(x -6) (x + 1) = 0
The solutions are 6 and – 1.
Clearing fractions:
\(\left(\frac{1}{x-6}+\frac{x}{x-2}\right)\) (x – 6) (x – 2) = \(\left(\frac{4}{(x-6)(x-2)}\right)\) (x – 6) (x – 2)
(x – 2) + x(x – 6) = 4
– 6x + x – 2 = 4
x2 – 5x -6 = 0
(x – 6) (x + 1) = 0
The solutions are 6 and – 1.
Because x is not allowed to be 6 in order to avoid division by zero, the solution 6 is extraneous; thus, – 1 is the only solution to the given rational equation.
Eureka Math Algebra 2 Module 1 Lesson 26 Problem Set Answer Key
Question 1.
Solve the following equations, and check for extraneous solutions.
a. \(\frac{x-8}{x-4}\) = 2
Answer:
0
b. \(\frac{4 x-8}{x-2}\) = 4
Answer:
All real numbers except 2
c. \(\frac{x-4}{x-3}\) = 1
Answer:
No solution
d. \(\frac{4 x-8}{x-2}\) = 3
Answer:
No solution
e. \(\frac{1}{2 a}-\frac{2}{2 a-3}\) = 0
Answer:
\(\)
f. \(\frac{3}{2 x+1}=\frac{5}{4 x+3}\)
Answer:
– 2
g. \(\frac{4}{x-5}-\frac{2}{5+x}=\frac{2}{x}\)
Answer:
\(-\frac{5}{3}\)
h. \(\frac{y+2}{3 y-2}+\frac{y}{y-1}=\frac{2}{3}\)
Answer:
\(\frac{5}{6}\), – 2
i. \(\frac{3}{x+1}-\frac{2}{1-x}\) = 1
Answer:
0, 5
j. \(\frac{4}{x-1}+\frac{3}{x}\) – 3 = 0
Answer:
\(\frac{1}{3}\), 3
k. \(\frac{x+1}{x+3}-\frac{x-5}{x+2}=\frac{17}{6}\)
Answer:
0, \(-\frac{55}{17}\)
l. \(\frac{x+7}{4}-\frac{x+1}{2}=\frac{5-x}{3 x-14}\)
Answer:
5, 6
m. \(\frac{b^{2}-b-6}{b^{2}}-\frac{2 b+12}{b}=\frac{b-39}{2 b}\)
Answer:
3, \(\frac{4}{3}\)
n. \(\frac{1}{p(p-4)}+1=\frac{p-6}{p}\)
Answer:
\(\frac{23}{6}\)
o. \(\frac{1}{a+3}=\frac{h+4}{h-2}+\frac{6}{h-2}\)
Answer:
– 8, – 4
p. \(\frac{m+5}{m^{2}+m}=\frac{1}{m^{2}+m}-\frac{m-6}{m+1}\)
Answer:
4, 1
Question 2.
Create and solve a rational equation that has 0 as an extraneous solution.
Answer:
One such equation is \(\frac{1}{x-1}+\frac{1}{x}=\frac{1}{x-x^{2}}\).
Question 3.
Create and solve a rational equation that has 2 as an extraneous solution.
Answer:
One such equation is \(\frac{1}{x-2}+\frac{1}{x+2}=\frac{4}{x^{2}-4}\).
Extension:
Question 4.
Two lengths a and b, where a > b, are in golden ratio if the ratio of a + b is to a is the same as a is to b. Symbolically, this is expressed as \(\frac{a}{b}=\frac{a+b}{a}\). We denote this common ratio by the Greek letter phi (pronounced “fee”) with symbol φ, so that If a and b are in common ratio, then φ = \(\frac{a}{b}=\frac{a+b}{a}\). By setting b = 1, we find that φ = a and φ is the positive number that satisfies the equation φ = \(\frac{\varphi+1}{\varphi}\) Solve this equation to find the numerical value for φ.
Answer:
We can apply either method from the previous lesson to solve this equation.
φ = \(\frac{\varphi+1}{\varphi}\)
φ2 = φ + 1
φ2 = φ + 1
φ2 – φ – 1 = 0
Applying the quadratic formula, we have two solutions:
φ = \(\frac{1+\sqrt{5}}{2}\) or φ = \(\frac{1-\sqrt{5}}{2}\)
Since φ is a positive number, and \(\frac{1-\sqrt{5}}{2}\) < 0, we have φ = \(\frac{1+\sqrt{5}}{2}\)
Question 5.
Remember that if we use x to represent an integer, then the next integer can be represented by x + 1.
a. Does there exist a pair of consecutive integers whose reciprocals sum to \(\frac{5}{6}\)? Explain how you know.
Answer:
Yes, 2 and 3 because \(\frac{1}{2}+\frac{1}{3}=\frac{3}{6}+\frac{2}{6}=\frac{5}{6}\)
b. Does there exist a pair of consecutive integers whose reciprocals sum to \(\frac{3}{4}\)? Explain how you know.
Answer:
If x represents the first integer, then x + 1 represents the next integer. Suppose \(\frac{1}{x}+\frac{1}{x+1}=\frac{3}{4}\). Then,
\(\frac{1}{x}+\frac{1}{x+1}=\frac{3}{4}\)
\(\frac{4(x+1)+4 x}{4 x(x+1)}=\frac{3 x(x+1)}{4 x(x+1)}\)
8x + 4 = 3x2 + 3x
3x2 – 5x – 4 = 0.
The solutions to this quadratic equation are \(\frac{5+\sqrt{73}}{6}\) and \(\frac{5-\sqrt{73}}{6}\), so there are no integers that solve this equation. Thus, there are no pairs of consecutive integers whose reciprocals sum to \(\frac{3}{4}\).
c. Does there exist a pair of consecutive even integers whose reciprocals sum to \(\frac{3}{4}\)? Explain how you know.
Answer:
If x represents the first integer, then x + 2 represents the next even integer. Suppose \(\frac{1}{x}+\frac{1}{x+2}=\frac{3}{4}\). Then,
\(\frac{1}{x}+\frac{1}{x+2}=\frac{3}{4}\)
\(\frac{4(x+2)+4 x}{4 x(x+2)}=\frac{3 x(x+2)}{4 x(x+2)}\)
8x + 8 = 3x2 + 6x
3x2 – 2x – 8 = 0.
The solutions to this quadratic equation are –\(\frac{4}{3}\) and 2; therefore, the only even integer x that solves the equation is 2. Then, 2 and 4 are consecutive even integers whose reciprocals sum to \(\frac{3}{4}\).
d. Does there exist a pair of consecutive even integers whose reciprocals sum to \(\frac{5}{6}\)? Explain how you know.
Answer:
If x represents the first integer, then x + 2 represents the next even integer. Suppose \(\frac{1}{x}+\frac{1}{x+2}=\frac{5}{6}\). Then,
\(\frac{1}{x}+\frac{1}{x+2}=\frac{5}{6}\)
\(\frac{6(x+2)+6 x}{6 x(x+2)}=\frac{5 x(x+2)}{6 x(x+2)}\)
12x + 12 = 5x2 + 10x
5x2 – 2x – 12 = 0.
The solutions to this quadratic equation are \(\frac{1+\sqrt{61}}{5}\) and \(\frac{1+\sqrt{61}}{5}\), so there are no integers that solve this equation. Thus, there are no pairs of consecutive even integers whose reciprocals sum to \(\frac{5}{6}\).
Eureka Math Algebra 2 Module 1 Lesson 26 Exit Ticket Answer Key
Find all solutions to the following equation. If there are any extraneous solutions, identify them and explain why they are extraneous.
\(\frac{7}{b+3}+\frac{5}{b-3}=\frac{10 b}{b^{2}-9}\)
Answer:
First, note that we must have x ≠ 3 and x ≠ – 3.
Using the equating numerators method: \(\frac{7(b-3)}{(b-3)(b+3)}+\frac{5(b+3)}{(b-3)(b+3)}=\frac{10 b}{(b-3)(b+3)}\)
Matching numerators, we have 7b – 21 + Sb + 15 = 10b, which leads to 12b – 6 = 10b; therefore, b = 3.
However, since the excluded values are 3 and – 3, the solution 3 is an extraneous solution, and there is no solution to \(\frac{7}{b+3}+\frac{5}{b-3}=\frac{10 b}{b^{2}-9}\).