Engage NY Eureka Math Algebra 2 Module 1 Lesson 25 Answer Key
Eureka Math Algebra 2 Module 1 Lesson 25 Example Answer Key
Example 1.
Perform the indicated operations below and simplify.
a. \(\frac{a+b}{4}+\frac{2 a-b}{5}\)
Answer:
A common multiple of 4 and 5 is 20, so we can write each expression as an equivalent rational expression with denominator 20. We have \(\frac{a+b}{4}=\frac{5 a+5 b}{20}\) and \(\frac{2 a-b}{5}=\frac{8 a-4 b}{20}\) so that
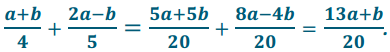
b. \(\frac{4}{3 x}-\frac{3}{5 x^{2}}\)
Answer:
A common multiple of 3x and 5x2 is 15x2, so we can write each expression as an equivalent rational expression with denominator 15x2. We have \(\frac{4}{3 x}-\frac{3}{5 x^{2}}\) = \(\frac{20 x}{15 x^{2}}-\frac{9}{15 x^{2}}\) = \(\frac{20 x-9}{15 x^{2}}\)
c. \(\frac{3}{2 x^{2}+2 x}+\frac{5}{x^{2}-3 x-4}\)
Answer:
Since 2x2 + 2x = 2x(x + 1) and x2 – 3x – 4 = (x – 4)(x + 1), a common multiple of 2x2 + 2x and x2 – 3x -4 is 2x(x + 1)(x – 4). Then we have
\(\frac{3}{2 x^{2}+2 x}+\frac{5}{x^{2}-3 x-4}\) = \(\frac{3(x-4)}{2 x(x+1)(x-4)}+\frac{5 \cdot 2 x}{2 x(x+1)(x-4)}\) = \(\frac{13 x-12}{2 x(x+1)(x-4)}\)
Example 2.
Simplify the following expression.
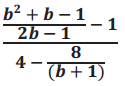
Answer:
First, we can rewrite the complex fraction as a division problem, remembering to add parentheses.

Remember that to divide rational expressions, we multiply by the reciprocal of the quotient. However, we first need to write each expression as a rational expression in lowest terms. For this, we need to find common denominators.
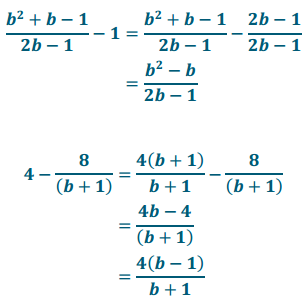
Now, we can substitute these equivalent expressions into our calculation above and continue to perform the division as we did in Lesson 24.
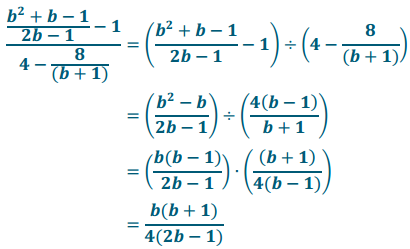
Eureka Math Algebra 2 Module 1 Lesson 25 Exercise Answer Key
Exercise 1.
Calculate the following sum: \(\frac{3}{10}+\frac{6}{10}\)
Answer:
One approach to this calculation is to factor out \(\frac{1}{10}\) from each term.
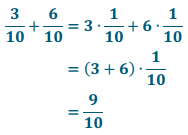
Exercise 2.
\(\frac{3}{20}-\frac{4}{15}\)
Answer:
![]()
Exercise 3.
\(\frac{\pi}{4}+\frac{\sqrt{2}}{5}\)
Answer:
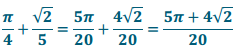
Exercise 4.
\(\frac{a}{m}+\frac{b}{2 m}-\frac{c}{m}\)
Answer:
![]()
Exercise 5 – 8
Perform the indicated operations for each problem below.
Exercise 5.
\(\frac{5}{x-2}+\frac{3 x}{4 x-8}\)
Answer:
A common multiple is 4 (x – 2).
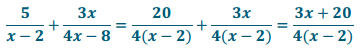
Exercise 6.
\(\frac{7 m}{m-3}+\frac{5 m}{3-m}\)
Answer:
Notice that (3 – m) = – (m – 3)
A common multiple is (m – 3)
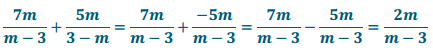
Exercise 7.
\(\frac{b^{2}}{b^{2}-2 b c+c^{2}}-\frac{b}{b-c}\)
Answer:
A common multiple is (b – c) (b – c)
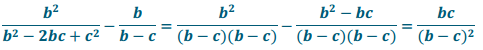
Exercise 8.
\(\frac{x}{x^{2}-1}-\frac{2 x}{x^{2}+x-2}\)
Answer:
A common multiple is (x – 1) (x + 1) (x + 2)
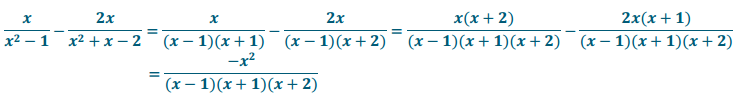
Eureka Math Algebra 2 Module 1 Lesson 25 Problem Set Answer Key
Question 1.
Write each sum or difference as a single rational expression.
a. \(\frac{7}{8}-\frac{\sqrt{3}}{5}\)
Answer:
\(\frac{35-8 \sqrt{3}}{40}\)
b. \(\frac{\sqrt{5}}{10}+\frac{\sqrt{2}}{6}+2\)
Answer:
\(\frac{3 \sqrt{5}+5 \sqrt{2}+60}{30}\)
c. \(\frac{4}{x}+\frac{3}{2 x}\)
Answer:
\(\frac{11}{2 x}\)
Question 2.
Write as a single rational expression.
a. \(\frac{1}{x}-\frac{1}{x-1}\)
Answer:
\(-\frac{1}{x(x-1)}\)
b. \(\frac{3 x}{2 y}-\frac{5 x}{6 y}+\frac{x}{3 y}\)
Answer:
\(\frac{x}{y}\)
c. \(\frac{a-b}{a^{2}}+\frac{1}{a}\)
Answer:
\(\frac{2 a-b}{a^{2}}\)
d. \(\frac{1}{p-2}-\frac{1}{p+2}\)
Answer:
\(\frac{4}{(p-2)(p+2)}\)
e. \(\frac{1}{p-2}+\frac{1}{2-p}\)
Answer:
0
f. \(\frac{1}{b+1}-\frac{b}{1+b}\)
Answer:
\(\frac{1-b}{b+1}\)
g. \(1-\frac{1}{1+p}\)
Answer:
\(\frac{p}{1+p}\)
h. \(\frac{p+q}{p-q}-2\)
Answer:
\(\frac{3 q-p}{p-q}\)
i. \(\frac{r}{s-r}+\frac{s}{r+s}\)
Answer:
\(\frac{r^{2}+s^{2}}{(s-r)(r+s)}\)
j. \(\frac{3}{x-4}+\frac{2}{4-x}\)
Answer:
\(\frac{1}{x-4}\)
k. \(\frac{3 n}{n-2}+\frac{3}{2-n}\)
Answer:
\(\frac{3 n-3}{n-2}\)
l. \(\frac{8 x}{3 y-2 x}+\frac{12 y}{2 x-3 y}\)
Answer:
– 4
m.

Answer:
\(-\frac{1}{m+2 n}\)
n.
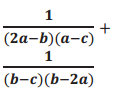
Answer:
\(\frac{b-a}{(a-c)(b-c)(2 a-b)}\)
o. \(\frac{b^{2}+1}{b^{2}-4}+\frac{1}{b+2}+\frac{1}{b-2}\)
Answer:
\(\frac{b^{2}+2 b+1}{(b-2)(b+2)}\)
Question 3.
Write each rational expression as an equivalent rational expression in lowest terms.
a.
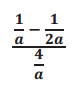
Answer:
\(\frac{1}{8}\)
b.
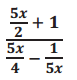
Answer:
\(\frac{10 x}{5 x-2}\)
c.

Answer:
\(\frac{x+2}{x-3}\)
Extension:
Question 4.
Suppose that x ≠ 0 and y ≠ 0. We know from our work in this section that \(\frac{1}{x} \cdot \frac{1}{y}\) is equivalent to \(\frac{1}{x y}\). Is It also true that \(\frac{1}{x}+\frac{1}{y}\) is equivalent to \(\frac{1}{x+y}\)? ProvIde evidence to support your answer.
Answer:
No, the rational expressions \(\frac{1}{x}+\frac{1}{y}\) and \(\frac{1}{x+y}\) are not equivalent. Consider x = 2 and y = 1. Then \(\frac{1}{x+y}=\frac{1}{2+1}=\frac{1}{3}\), but \(\frac{1}{x}+\frac{1}{y}=\frac{1}{2}+1=\frac{3}{2}\). Since \(\frac{1}{3} \neq \frac{3}{2}\), the expressions \(\frac{1}{x}+\frac{1}{y}\) and \(\frac{1}{x+y}\) are not equivalent.
Question 5.
Suppose that x = \(\) and y = \(\) Show that the value of x2 + y2 does not depend on the value of t.
Answer:

Since x2 + y2 = 1, the value of x2 + y2 does not depend on the value of t.
Question 6.
Show that for any real numbers a and b, and any integers x and y so that x ≠ 0, y ≠ 0, x ≠ y, and x ≠ – y,
![]()
Answer:
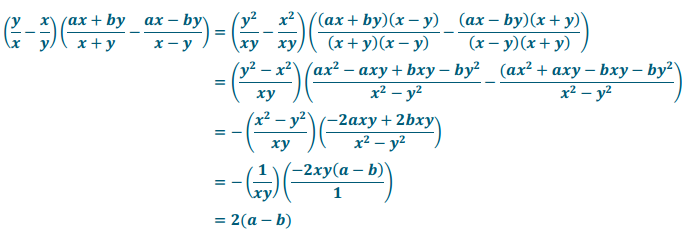
Question 7.
Suppose that n is a positive integer.
a. Rewrite the product in the form \(\frac{P}{Q}\) for polynomials P and Q: \(\left(1+\frac{1}{n}\right)\left(1+\frac{1}{n+1}\right)\)
Answer:
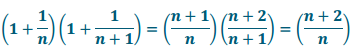
b. Rewrite the product in the form \(\frac{P}{Q}\) for polynomials P and Q: \(\left(1+\frac{1}{n}\right)\left(1+\frac{1}{n+1}\right)\left(1+\frac{1}{n+2}\right)\)
Answer:
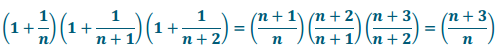
c. Rewrite the product in the form \(\frac{P}{Q}\) for polynomials P and Q:
![]()
Answer:
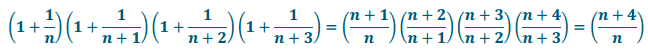
d. If this pattern continues, what is the product of n of these factors?
Answer:
If we have n of these factors, then the product will be
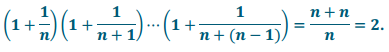
Eureka Math Algebra 2 Module 1 Lesson 25 Exit Ticket Answer Key
Perform the indicated operation.
Question 1.
\(\frac{3}{a+2}+\frac{4}{a-5}\)
Answer:
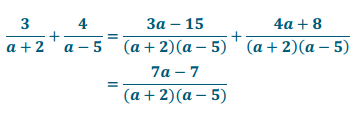
Question 2.
\(\frac{4 r}{r+3}-\frac{5}{r}\)
Answer:
