Engage NY Eureka Math Algebra 2 Module 1 Lesson 19 Answer Key
Eureka Math Algebra 2 Module 1 Lesson 19 Exercise Answer Key
Exercise 1.
Consider the polynomial function f(x) = 3x2 + 8x – 4.
a. Divide f by x – 2.
Answer:
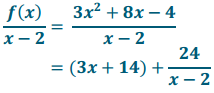
Answer:
b. Find f(2)
Answer:
f(2) = 24
Exercise 2.
Consider the polynomial function g(x) = x3 – 3x2 + 6x + 8.
a. Divide g by x + 1.
Answer:

b. Find g(-1).
Answer:
g(-1) = – 2
Exercise 3.
Consider the polynomial function h(x) = x3 + 2x – 3.
a. Divide h by x – 3.
Answer:
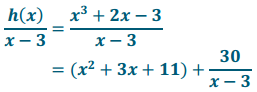
b. Find h(3)
Answer:
h(3) = 30
Exercise 4.
Consider the polynomial P(x) = x3 + kx2 + x + 6.
a. Find the value of k so that x + 1 is a factor of P.
Answer:
In order for x + 1 to be a factor of P, the remainder must be zero. Hence, since x + 1 = x – ( – 1), we must have P( – 1) = 0 so that 0 = – 1 + k – 1 + 6.
Then k = – 4.
b. Find the other two factors of P for the value of k found in part (a).
Answer:
P(x) = (x + 1)(x2 – 5x + 6) = (x + 1) (x – 2) (x – 3)
Exercise 5.
Consider the polynomial P(x) = x4 + 3x3 – 28x2 – 36x + 144.
a. Is 1 a zero of the polynomial P?
Answer:
No
b. Is x + 3 one of the factors of P?
Answer:
Yes; P(- 3) = 81 – 81 – 252 + 108 + 144 = 0.
c. The graph of P is shown to the right. What are the zeros of P?
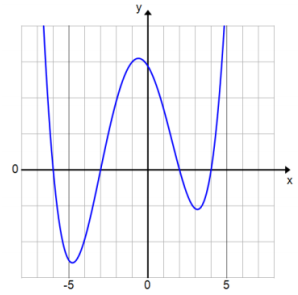
Answer:
Approximately – 6, – 3, 2, and 4.
d. Write the equation of P in factored form.
Answer:
P(x) = (x + 6) (x + 3) (x – 2) (x – 4)
Exercise 6.
Consider the graph of a degree 5 polynomial shown to the right, with x-intercepts – 4, – 2, 1, 3, and 5.
a. Write a formula for a possible polynomial function that the graph represents using c as the constant factor.

Answer:
P(x) = c(x + 4) (x + 2) (x – 1) (x – 3) (x – 5)
b. Suppose the y-intercept is – 4. Find the value of c so that the graph f P has y-intercept – 4.
Answer:
P(x) = \(\frac{1}{30}\) (x + 4) (x + 2) (x – 1) (x – 3) (x – 5)
Eureka Math Algebra 2 Module 1 Lesson 19 Problem Set Answer Key
Question 1.
Use the remainder theorem to find the remainder for each of the following divisions.
a. \(\frac{\left(x^{2}+3 x+1\right)}{(x+2)}\)
Answer:
– 1
b. \(\frac{x^{3}-6 x^{2}-7 x+9}{(x-3)}\)
Answer:
– 39
c. \(\frac{32 x^{4}+24 x^{3}-12 x^{2}+2 x+1}{(x+1)}\)
Answer:
– 5
d. \(\frac{32 x^{4}+24 x^{3}-12 x^{2}+2 x+1}{(2 x-1)}\)
Hint for part (d): Can you rewrite the division expression so that the divisor is in the form (x – c) for some constant c?
Answer:
4
Question 2.
Consider the polynomial P(x) = x3 + 6x2 – 8x – 1. Find P(4) in two ways.
Answer:
P(4) = 43 + 6(4)2 – 8(4) – 1 = 127 \(\frac{x^{3}+6 x^{2}-8 x-1}{x-4}\) has a remainder of 127, so P(4) = 127.
Question 3.
Consider the polynomial function P(x) = 2x4 + 3x2 + 12.
a. Divide P by x + 2, and rewrite P in the form (divisor) (quotient) + remainder.
Answer:
P(x) = (x + 2) (2x3 – 4x2 + 11x – 22) + 56
b. Find P(- 2).
Answer:
P(- 2) = (- 2 + 2) (q(- 2)) + 56 = 56
Question 4.
Consider the polynomial function P(x) = x3 + 42.
a. Divide P by x – 4, and rewrite P In the form (divisor)(quotient) + remainder.
Answer:
P(x) = (x – 4) (x2 + 4x + 16) + 106
b. Find P(4).
Answer:
P(4) = (4 – 4) (q(4)) + 106 = 106
Question 5.
Explain why for a polynomial function P, P(a) is equal to the remainder of the quotient of P and x – a.
Answer:
The polynomial P can be rewritten in the form P(x) = (x – a) (q(x)) + r, where q(x) is the quotient function and r is the remainder. Then P(a) = (a – a) (q(a)) + r. Therefore, P(a) = r.
Question 6.
Is x – 5 a factor of the function f(x) = x3 + x2 – 27x – 15? Show work supporting your answer.
Answer:
Yes, because f(5) = 0 means that dividing by x – 5 leaves a remainder of 0.
Question 7.
Is x + 1 a factor of the function f(x) = 2x5 – 4x4 + 9x3 – x + 13? Show work supporting your answer.
Answer:
No, because f(- 1) = – 1 means that dividing by x + 1 has a remainder of – 1.
Question 8.
A polynomial function p has zeros of 2, 2, -3, -3, 3, and 4. Find a possible formula for P, and state its degree. Why is the degree of the polynomial not 3?
Answer:
0ne solution is P(x) = (x – 2)2 (x + 3)3 (x – 4). The degree of P is 6. This is not a degree 3 polynomial function because the factor (x – 2) appears twice, and the factor (x + 3) appears 3 times, while the factor (x – 4) appears once.
Question 9.
Consider the polynomial function P(x) = x3 – 8x2 – 29x + 180.
a. Verify that P(9) = 0. Since P(9) = 0 what must one of the factors of P be?
Answer:
P(9)= 93 – 8(92) – 29(9) + 180 0; x – 9
b. Find the remaining two factors of P.
Answer:
P(x) = (x – 9) (x – 4) (x + 5)
c. State the zeros of P.
Answer:
x = 9, 4, – 5
d. Sketch the graph of P.

Answer:

Question 10.
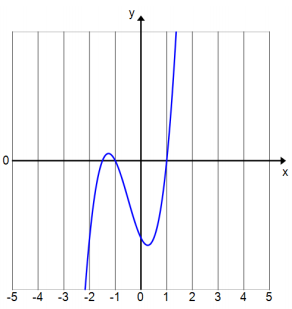
Consider the polynomial function P(x) = 2x3 + 3x2 – 2x – 3.
a. Verify that P(-1) = 0. Since P(-1) = 0, what must one of the factors of P be?
Answer:
P(- 1) = 2(- 1)3 + 3(- 1)2 – 2(- 1) – 3 = 0; x + 1
b. Find the remaining two factors of P.
Answer:
P(x) = (x + 1) (x – 1) (2x + 3)
c. State the zeros of P.
Answer:
x = – 1, 1, –\(\frac{3}{2}\)
d. Sketch the graph of P.

Answer:
Question 11.
The graph to the right is of a third-degree polynomial function f.

a. State the zeros off.
Answer:
x = – 10, – 1, 2
b. Write a formula for f in factored form using c for the constant factor.
Answer:
f(x) = c (x + 10) (x + 1) (x – 2)
c. Use the fact that f(- 4) = – 54 to find the constant factor c.
Answer:
– 54 = c(- 4 + 10) (- 4 + 1) (- 4 – 2)
c = – \(\frac{1}{2}\)
f(x) = – \(\frac{1}{2}\) (x + 10) (x + 1) (x – 2)
d. Verify your equation by using the fact that f(1) = 11.
Answer:
f(1) = – \(\frac{1}{2}\) (1 + 10)(1 + 1) (1 – 2) = – \(\frac{1}{2}\) (11) (2) (- 1) = 11
Question 12.
FInd the value of k so that \(\frac{x^{3}-k x^{2}+2}{x-1}\) has remainder 8.
Answer:
k = – 5
Question 13.
Find the value k so that \(\frac{k x^{3}+x-k}{x+2}\) has remainder 16.
Answer:
k = – 2
Question 14.
Show that x51 – 21x + 20 is divisible by x – 1.
Answer:
Let P(x) = x51 – 21x + 20.
Then P(1) = 151 – 21(1) + 20 = 1 – 21 + 20 = 0.
Since P(1) = 0, the remainder of the quotient (x51 – 21x + 20) ÷ (x – 1) is 0.
Therefore, x51 – 21 x + 20 is divisible by x – 1.
Question 15.
Show that x + 1 Is a factor of 19x42 + 18x – 1.
Answer:
LetP(x) = 19x42 + 18x -1.
Then P(- 1) = 19(-1)42 + 18(- 1) – 1 = 19 – 18 – 1 = 0.
Since P(- 1) = 0, x + 1 must be a factor of P.
Write a polynomial function that meets the stated conditions.
Question 16.
The zeros are – 2 and 1.
Answer:
p(x) = (x + 2)(x – 1) or, equivalently, p(x) = x<sup2</sup + x – 2
Question 17.
The zeros are – 1, 2, and 7.
Answer:
p(x) = (x + 1) (x – 2) (x – 7) or, equivalently, p(x) = x<sup3</sup – 8x<sup2</sup + 5x + 14
Question 18.
The zeros are – \(\frac{1}{2}\) and –\(\frac{3}{4}\).
Answer:
p(x) = (x + \(\frac{1}{2}\)) (x – \(\frac{3}{4}\)) or, equivalently, p(x) = x2 – \(\frac{x}{4}\) – \(\frac{3}{8}\)
Question 19.
The zeros are – \(\frac{2}{3}\) and 5, and the constant term of the polynomial is – 1o.
Answer:
p(x) = (x – 5)(3x + 2) or, equivalently, p(x) = 3x2 – 13x – 10
Question 20.
The zeros are 2 and –\(\frac{3}{2}\), the polynomial has degree 3, and there are no other zeros.
Answer:
p(x) = (x – 2)2 (2x + 3) or, equivalently, p(x) = (x – 2)(2x + 3)2
Eureka Math Algebra 2 Module 1 Lesson 19 Exit Ticket Answer Key
Consider polynomial P(x) = x3 + x2 – 10x – 10.
Question 1.
Is x + 1 one of the factors of P? Explain.
Answer:
P(- 1) = (- 1)3 + (- 1)2 – 10 (- 1) – 10
= – 1 + 1 + 10 – 10 = 0
Yes, x + 1 isa factor of P because P (-1) = 0. Or, using factoring by grouping, we have
P(x) = x2(x + 1) – 10 (x + 1) = (x + 1) (x2 – 10).
Question 2.
The graph shown has x-intercepts at √10, – 1 and – √10 Could this be the graph of P(x) = x3 + x2 – 10x – 10? Explain how you know.
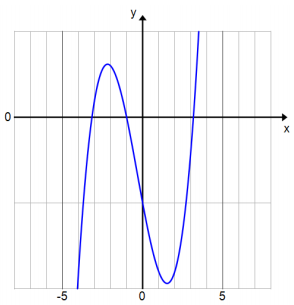
Answer:
Yes, this could be the graph of P. Since this graph has x-intercepts at √10 – 1, and – √10, the factor theorem says that (x – √10), (x – 1), and (x + √10) are all factors of the equation that goes with this graph. Since (x – √10) (x + √10) (x – 1) = x2 + x2 – 10x – 10, the graph shown is quite likely to be the graph of P.