Engage NY Eureka Math Algebra 1 Module 2 Lesson 7 Answer Key
Eureka Math Algebra 1 Module 2 Lesson 7 Exercise Answer Key
Classwork
Exploratory Challenge 1/Exercises 1–3: Skewed Data and Their Measure of Center
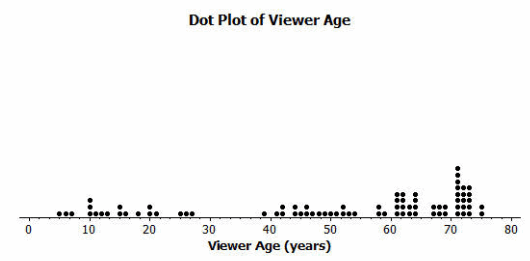
Consider the following scenario. A television game show, Fact or Fiction, was cancelled after nine shows. Many people watched the nine shows and were rather upset when it was taken off the air. A random sample of eighty viewers of the show was selected. Viewers in the sample responded to several questions. The dot plot below shows the distribution of ages of these eighty viewers.
Then, discuss the following:
What does the dot farthest to the left in this dot plot tell us?
→ This dot tells us that one of the 80 viewers surveyed is only about 5 years old.
→ Is this distribution symmetrical?
→ No. There are more viewers (a cluster of viewers) at the older ages.
→ What age would describe a typical age for this sample of viewers?
→ The typical age is around 70 years old.
→ A reviewer of this show indicated that it was a cross-generational show. What do you think that term means?
→ Viewers varied in age. People from more than one generation watched the show.
→ Do the data in the dot plot confirm or contradict the idea that it was a cross-generational show?
→ The data confirm this idea. They show that viewers from as young as 5 years to as old as 75 years watch this show.
→ What could be the reason for the cancellation of the show? Allow students to brainstorm ideas. If no one suggests it, provide the following as a possible reason:
→ Cross-generational shows are harder to get sponsors for. Sponsors like to purchase airtime for shows designed for their target audience.
Give careful attention to the use of language in the following discussion; transition from less formal to more formal. Begin by emphasizing the language of “Which side is stretched?” and “Which side has the tail?” Then, make a connection to the phrasing skewed to the left or left-skewed, meaning the data are stretched on the left side and/or have their tail on the left side.
→ A data distribution that is not symmetrical is described as skewed. In a skewed distribution, data “stretch” either to the left or to the right. The stretched side of the distribution is called a tail.
→ Would you describe the age data distribution as a skewed distribution?
→ Yes
→ Which side is stretched? Which side has the tail?
→ The left side is stretched. The tail is on the left side.
→ So, would you say it is skewed to the left or skewed to the right?
→ The data are stretched to the left, with the tail on the left side, so these are skewed to the left, or left-skewed.
Allow students to work independently or in pairs to answer Exploratory Challenge 1. Then, discuss and confirm answers as a class. The following are sample responses to Exercises 1–3:
Exercise 1.
Approximately where would you locate the mean (balance point) in the above distribution?
Answer:
An estimate that indicates an understanding of how the balance would need to be closer to the cluster points on the high end is addressing balance. An estimate around 45 to 60 would indicate that students are taking the challenge of balance into account.
Exercise 2.
How does the direction of the tail affect the location of the mean age compared to the median age?
Answer:
The tail is on the left, which means that the data are skewed to the left. The mean is typically in the direction of the tail, so the mean age would be to the left of the median age.
Exercise 3.
The mean age of the above sample is approximately 50. Do you think this age describes the typical viewer of this show? Explain your answer.
Answer:
Students should compare the given mean to their estimate. The mean as an estimate of a typical value does not adequately reflect the older ages of more than half the viewers.
Exploratory Challenge 2/Exercises 4–8: Constructing and Interpreting the Box Plot
Exercise 4.
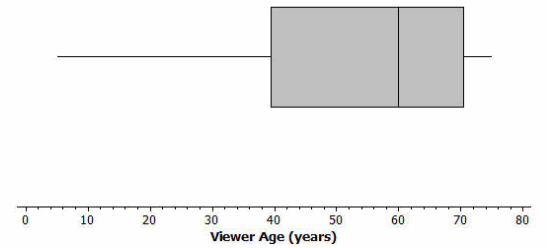
Using the above dot plot, construct a box plot over the dot plot by completing the following steps:
i. Locate the middle 40 observations, and draw a box around these values.
ii. Calculate the median, and then draw a line in the box at the location of the median.
iii. Draw a line that extends from the upper end of the box to the largest observation in the data set.
iv. Draw a line that extends from the lower edge of the box to the minimum value in the data set.
Students complete Exercises 5–8 and confirm answers with a peer or as a class.
Exercise 5.
Recall that the 5 values used to construct the dot plot make up the 5-number summary. What is the 5-number summary for this data set of ages?
Minimum age: __
Answer:
5
Lower quartile or Q1:___
Answer:
40
Median age: __
Answer:
60
Upper quartile or Q3: ___
Answer:
70
Maximum age: ___
Answer:
75
Exercise 6.
What percent of the data does the box part of the box plot capture?
Answer:
The box captures 50% of the viewers.
Exercise 7.
What percent of the data fall between the minimum value and Q1?
Answer:
25% of the viewers fall between the minimum value and Q1.
Exercise 8.
What percent of the data fall between Q3 and the maximum value?
Answer:
25% of the viewers fall between Q3 and the maximum value.
Exercises 9–14
An advertising agency researched the ages of viewers most interested in various types of television ads. Consider the following summaries:

Exercise 9.
The mean age of the people surveyed is approximately 50 years old. As a result, the producers of the show decided to obtain advertisers for a typical viewer of 50 years old. According to the table, what products or services do you think the producers will target? Based on the sample, what percent of the people surveyed about the Fact or Fiction show would have been interested in these commercials if the advertising table is accurate?
Answer:
The target audience would be viewers 46 to 55 years old, so the producers would focus on ads for financial services, appliances, and furniture. 12 out of 80 viewers, or 15%, are in that range.
Exercise 10.
The show failed to generate the interest the advertisers hoped. As a result, they stopped advertising on the show, and the show was cancelled. Kristin made the argument that a better age to describe the typical viewer is the median age. What is the median age of the sample? What products or services does the advertising table suggest for viewers if the median age is considered as a description of the typical viewer?
Answer:
The median age is 60 years old. The target audience based on the median would include the ages 56 to 72 years old. Target products for this group are retirement planning, cruises, and health-care services.
Exercise 11.
What percent of the people surveyed would be interested in the products or services suggested by the advertising table if the median age were used to describe a typical viewer?
Answer:
31 of the 80 viewers are 56 to 72 years old, or approximately 39%.
Exercise 12.
What percent of the viewers have ages between Q1 and Q3? The difference between Q3 and Q1, or Q3 – Q1, is called the interquartile range, or IQR. What is the IQR for this data distribution?
Answer:
Approximately 50% of the viewers are located between Q1 and Q3. The IQR is 70-40, or 30 years.
Exercise 13.
The IQR provides a summary of the variability for a skewed data distribution. The IQR is a number that specifies the length of the interval that contains the middle half of the ages of viewers. Do you think producers of the show would prefer a show that has a small or large interquartile range? Explain your answer.
Answer:
A smaller IQR indicates less variability, so it may be easier to target advertisements to a particular group.
A larger IQR indicates more variability, which means the show is popular across generations but harder to target advertising.
Exercise 14.
Do you agree with Kristin’s argument that the median age provides a better description of a typical viewer? Explain your answer.
Answer:
The median is a better description of a typical viewer for this audience because the distribution is skewed.
Exploratory Challenge 3/Exercises 15–20: Outliers
Students at Waldo High School are involved in a special project that involves communicating with people in Kenya. Consider a box plot of the ages of 200 randomly selected people from Kenya.
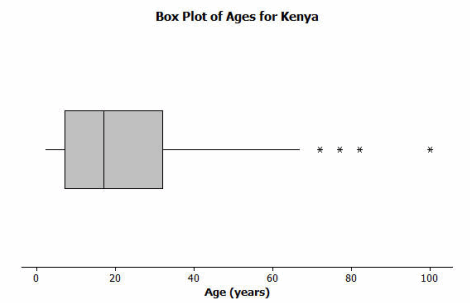
A data distribution may contain extreme data (specific data values that are unusually large or unusually small relative to the median and the interquartile range). A box plot can be used to display extreme data values that are identified as outliers.
Each “*” in the box plot represents the ages of four people from this sample. Based on the sample, these four ages were considered outliers.
Exercise 15.
Estimate the values of the four ages represented by an *.
Answer:
Allow for reasonable estimates. For example, 72, 77, 82, and 100 years old would be reasonable estimates.
An outlier is defined to be any data value that is more than 1.5×(IQR) away from the nearest quartile.
Exercise 16.
What is the median age of the sample of ages from Kenya? What are the approximate values of Q1 and Q3? What is the approximate IQR of this sample?
Answer:
The median age is approximately 18 years old. Q1 is approximately 7 years old, and Q3 is approximately 32 years old. The approximate IQR is 25 years.
Exercise 17.
Multiply the IQR by 1.5. What value do you get?
Answer:
1.5×25 is 37.5 years.
Exercise 18.
Add 1.5×(IQR) to the third quartile age (Q3). What do you notice about the four ages identified by an *?
Answer:
37.5 years + 32 years is 69.5 years, or approximately 70 years. The four ages identified by an * are all greater than this value.
Exercise 19.
Are there any age values that are less than Q1-1.5×(IQR)? If so, these ages would also be considered outliers.
Answer:
7 years – 37.5 years is -30.5 years. There are no ages less than this value.
Exercise 20.
Explain why there is no * on the low side of the box plot for ages of the people in the sample from Kenya.
Answer:
An outlier on the lower end would have to be a negative age, which is not possible.
Eureka Math Algebra 1 Module 2 Lesson 7 Problem Set Answer Key
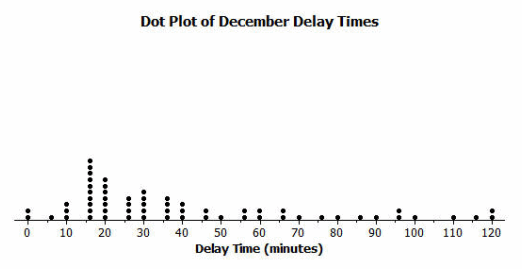
Consider the following scenario. Transportation officials collect data on flight delays (the number of minutes a flight takes off after its scheduled time).
Consider the dot plot of the delay times in minutes for 60 BigAir flights during December 2012:
Question 1.
How many flights left more than 60 minutes late?
Answer:
14 flights left more than 60 minutes late.
Question 2.
Why is this data distribution considered skewed?
Answer:
This is a skewed distribution because there is a stretch of flights located to the right.
Question 3.
Is the tail of this data distribution to the right or to the left? How would you describe several of the delay times in the tail?
Answer:
The tail is to the right. The delay times in the tail represent flights with the longest delays.
Question 4.
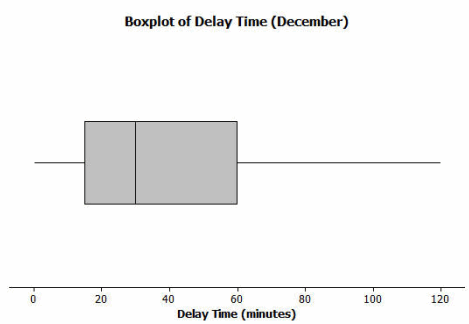
Draw a box plot over the dot plot of the flights for December.
Answer:
A box plot of the December delay times is as follows:
Question 5.
What is the interquartile range, or IQR, of this data set?
Answer:
The IQR is approximately 60-15, or 45 minutes.
Question 6.
The mean of the 60 flight delays is approximately 42 minutes. Do you think that 42 minutes is typical of the number of minutes a BigAir flight was delayed? Why or why not?
Answer:
The mean value of 42 minutes is not a good description of a typical flight delay. It is pulled upward to a larger value because of flights with the very long delays.
Question 7.
Based on the December data, write a brief description of the BigAir flight distribution for December.
Answer:
Students should include a summary of the data in their reports. Included should be the median delay time of 30 minutes and that 50% of the flights are delayed between 15 minutes to 60 minutes, with a typical delay of approximately 30 minutes.
Question 8.
Calculate the percentage of flights with delays of more than 1 hour. Were there many flight delays of more than 1 hour?
Answer:
14 flights were delayed more than 60 minutes, or 1 hour. These 14 flights represent approximately 23% of the flights. This is not a large number, although the decision of whether or not 23% is large is subjective.
Question 9.
BigAir later indicated that there was a flight delay that was not included in the data. The flight not reported was delayed for 48 hours. If you had included that flight delay in the box plot, how would you have represented it? Explain your answer.
Answer:
A flight delay of 48 hours would be much larger than any delay in this data set and would be considered an extreme value, or outlier. To include this flight would require an extension of the scale to 2,880 minutes. This flight might have been delayed due to an extreme mechanical problem with the plane or an extended problem with weather.
Question 10.
Consider a dot plot and the box plot of the delay times in minutes for 60 BigAir flights during January 2013.
How is the January flight delay distribution different from the one summarizing the December flight delays? In terms of flight delays in January, did BigAir improve, stay the same, or do worse compared to December? Explain your answer.
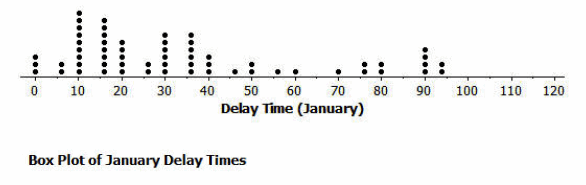
Answer:
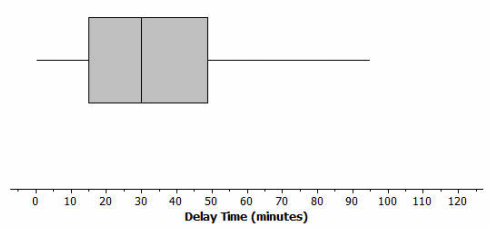
The median flight delay is the same as in December, which is 30 minutes. The IQR is less, or approximately 35 minutes. The maximum is also less. In general, this indicates a typical delay of 30 minutes with less variability.
Eureka Math Algebra 1 Module 2 Lesson 7 Exit Ticket Answer Key
Question 1.
A data set consisting of the number of hours each of 40 students watched television over the weekend has a minimum value of 3 hours, a Q1 value of 5 hours, a median value of 6 hours, a Q3 value of 9 hours, and a maximum value of 12 hours. Draw a box plot representing this data distribution.

Answer:
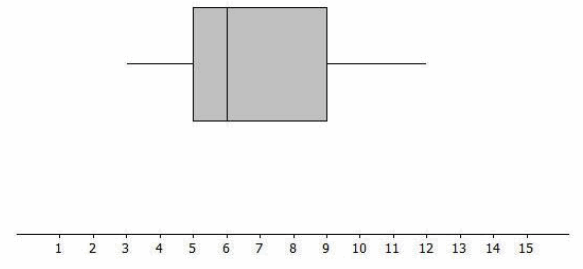
Students should sketch a box plot with the minimum value at 3 hours, a Q1 at 5 hours, a median at 6 hours, a Q3
at 9 hours, and a maximum value at 12 hours.
Question 2.
What is the interquartile range (IQR) for this distribution? What percent of the students fall within this interval?
Answer:
The interquartile range is 4 hours. 50% of the students fall within this interval.
Question 3.
Do you think the data distribution represented by the box plot is a skewed distribution? Why or why not?
Answer:
You would speculate that this distribution is skewed because 50% of the data would be between 3 and 6 hours, while 50% would be between 6 and 12 hours. There would be the same number of dots in the smaller interval from 3 to 6 as there would be in the wider interval of 6 to 12.
Question 4.
Estimate the typical number of hours students watched television. Explain why you chose this value.
Answer:
Since this is a skewed data distribution, the most appropriate estimate of a typical number of hours would be the median, or 6 hours.