The geometric transformation is a bijection of a set that has a geometric structure by itself. It changes the appearance of a shape but the geometric figures can be congruent or similar to its preimage. Enlargement means enlarging the shape and changing its size. The complete details about the enlargement transformation of triangles and their solved problems are given here.
Enlargement Transformation Definition
The transformation could be rigid and non-rigid. The four types of transformations are rotation, dilation, translation, and reflection. After all the transformations, the shapes have the same size, angle, lengths and area.
Enlargement means increasing or decreasing the size of the shape. It is an example of transformation. Every triangle has been enlarged by a scale factor. To enlarge a shape, the centre of enlargement is required. The distances from the centre to each point are multiplied by the scale factor to get enlarged.
Similarity on Transformation Enlargement
Here we will discuss the similarity in enlargement transformation.
Let us cut a geometrical shape such as a triangle from a piece of cardboard. Hold those triangles one after the other between a point source of light and a wall. Check out the shadow cast by each figure on the wall. The shadows will have the same shapes as the original triangles but in a larger size. The shadows are said to be similar to the original triangles.
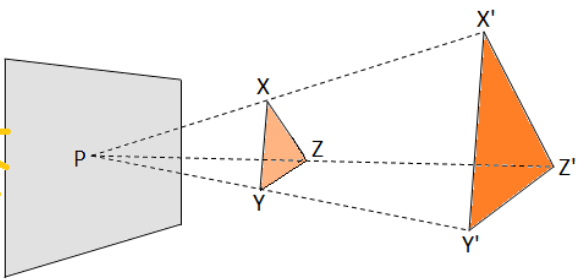
In the above figure, XYZ is a triangle and its shadow is X’Y’Z’.
We can say that ∠X = ∠X’, ∠Y = ∠Y’, ∠Z = ∠Z’
Two triangles are equiangular.
The shadow X’Y’Z’ is an enlarged image of XYZ. If the side X’Y’ = k x XY, Y’Z’ = k x YZ, Z’X’ = k x ZX
\(\frac { X’Y’ }{ XY } \) = \(\frac { Y’Z’ }{ YZ } \) = \(\frac { Z’X’ }{ ZX } \) = k
Here, k is the scale factor
The point p is the centre of enlargement.
Questions on Enlargement Transformation
Question 1:
A triangle ABC has been enlarged by a scale factor of 3 to a triangle A’B’C’. Find the length of A’B’ if AB = 5 cm and AC if A’C’ = 8 cm.
Solution:
Let \(\frac { A’B’ }{ AB } \) = \(\frac { B’C’ }{ BC } \) = \(\frac { A’C’ }{ AC } \) = k
\(\frac { A’B’ }{ AB } \) = k
\(\frac { A’B’ }{ 5 } \) = 3
A’B’ = 3 x 5 = 15 cm
\(\frac { A’C’ }{ AC } \) = k
\(\frac { 8 }{ AC } \) = 3
AC = 8 x 3 = 24 cm
Question 2:
A triangle XYZ has been enlarged to ∆X’Y’Z’ about the centre of enlargement O by a scale factor of 4.2. Find
(i) X’Y’ if XY = 5 cm
(ii) XZ if X’Z’ = 12 cm
(iii) OX’ and XX’ if OX = 2 cm
Solution:
(i) \(\frac { X’Y’ }{ XY } \) = k
\(\frac { X’Y’ }{ 5 } \) = 4.2
X’Y’ = 4.2 x 5
= 21
(ii) \(\frac { X’Z’ }{ XZ } \) = k
\(\frac { 12 }{ XZ } \) = 4.2
XZ = 12 x 4.2
= 50.4
(iii) \(\frac { OX’ }{ OX } \) = k
\(\frac { OX’ }{ 2 } \) = 4.2
OX’ = 4.2 x 2
= 8.4
XX’ = OX’ – OX = 8.4 – 2 = 6.4 cm
FAQ’s on Transformation Enlargement
1. What happens when a shape enlarge by a negative number?
An enlargement with a negative scale factor gives an image on the other side of the centre of enlargement.
2. What is the centre of enlargement?
Enlarging a shape changes its size. A centre of enlargement is required to enlarge a shape. When a shape is enlarged from a centre of enlargement, the distances from the centre to each point are multiplied by the scale factor.
3. Define scale factor?
The scale factor describes the size of enlargement or reduction of the shape. It is the ratio of a bigger size to a smaller size.
4. What are the types of transformations?
The different types of transformations are rotation, reflection, dilation, and translation.
