Polygon is a two-dimensional geometric figure which has a finite number of sides. Each side of the polygon is a straight line and all line segments form a closed figure. Convex and Concave Polygons are the two different types of polygons. A polygon that has all the interior angles lesser than 180°, then it is called the convex polygon. If the polygon contains one or more interior angles greater than 180°, then it is called the concave polygon. Check out the definitions, properties, and examples in the remaining sections of this article.
Convex and Concave Polygons
A polygon is said to be a convex polygon when the measures of the interior angles are lesser than 180 degrees. The vertices of the convex polygon always point outwards.
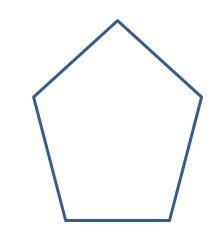
A polygon that measures at least one angle greater than 180 degrees is called the concave polygon. The vertices of this are inwards and outwards also. Convex, concave polygons are opposite to each other.

Other Types of Polygons
The various types of polygons are described here with their definitions.
- Regular polygons: All sides of the polygons measure equal dimensions.
- Irregular Polygons: All sides of the polygons measure unequal dimensions.
- Quadrilateral Polygons: It is a four-sided quadrilateral
- Convex Polygons: Examples are rhombus, parallelogram, square, rectangle, pentagon, etc
- Concave Polygons
Also, read Regular and Irregular Polygons
Regular Convex Polygons
A regular convex polygon has all sides of equal length, all interior angles are the same and below 180 degrees. The distance between the center point to all vertices is equal. An example is square.
Irregular, Regular Concave Polygons
All the concave polygons are irregular concave polygons. Because concave polygons must have at least one angle greater than 180 degrees and irregular polygons measure interior angles differently. There is no concave polygon that is regular.
Convex and Concave Polygons – Formulas
The perimeter of a convex and concave polygon is the sum of all sides or the total region coved around the boundary.
Perimeter = Sum of all sides
Area of convex polygon is given as A = ½ | (x₁ • y₂ – x₂ • y₁) + (x₂ • y₃ – x₃ • y₂) + . . . + (xn • y₁ – x₁ • yn) |
Where (x₁, y₁), (x₂, y₂), (x₃, y₃), . . . (xn, yn) are the vertices of the convex polygon
Area of a concave polygon
Like regular polygons, there is no formula to calculate the area of the irregular concave polygons. Here, on each side, interior angles will be of different lengths. So, we need to split the polygons into triangles or other shapes to find the area.
Properties of Concave and Convex Polygons
- The interior angles of convex polygons have to be less than 180 degrees. The concave polygon should have at least one reflex angle.
- A concave polygon must have one vertex that points inwards to give the concave shape.
- Sum of all interior angles of the convex polygon of n sides = (n – 2) x 180°
- If a line segment is drawn crossing the concave polygon, then it will intersect the boundary more than two times.
- Concave polygons have more than one diagonal that lie outside the boundary.
- Concave polygons need to have one pair of sides joining a vertex that goes outside the vertex.
Interior, Exterior Angles
The interior angles are defined as the angles inside the polygon. The number of interior and exterior angles in a polygon are the same. According to the convex and concave polygon sum formula, for any n sided polygon, the sum of interior angles is (n – 2)180°. By knowing the sum, divide the sum by a total number of sides to get each interior angle measurement.
The exterior angle is defined as the angle formed by extending the side of the polygon. We already know that the sum of exterior angles of any polygon is 360°. Divide the sum by the total number of sides to get the measure of each exterior angle of Convex and Concave Polygons.
Examples of Convex and Concave Polygon
Example 1:
Find the area of the convex polygon with three sides, and vertices are (5, 7), (8, 4), (-2, 1).
Solution:
Given that,
Vertices of the polygon are (5, 7), (8, 4), (-2, 1).
(x₁, y₁) = (5, 7), (x₂, y₂) = (8, 4), (x₃, y₃) = (-2, 1)
The formula to calculate the area of a convex polygon is A = ½ | (x₁ • y₂ – x₂ • y₁) + (x₂ • y₃ – x₃ • y₂) + (x₃ • y₁ – x₁ • y₃) |
= ½ | (5 • 4 – 8 • 7) + (8 • 1 – (-2) • 4) + (-2 • 7 – 5 • 1) |
= ½ | (20 – 56) + (8 + 8) + (-14 – 5) |
= ½ | -36 + 16 – 19 |
= ½ | -55 + 16 |
= ½ | -39 |
= 19.5
Therefore, the area is 19.5 sq units.
Example 2:
Calculate the perimeter and area of the pentagon has a side length of 4 cm.
Solution:
Given that,
The side length of pentagon s = 4 cm
n = 5
The regular polygon area formula is A = n x s² x cot(π/n) / 4
A = 5 x 4² x cot(π/5) / 4
= 5 x 16 x 1.3763 / 4
= 110.104 / 4
= 27.526 cm²
Perimeter p = Sum of all sides
= 4 + 4 + 4 + 4 + 4
= 20 cm
Hence the area, perimeter of the pentagon is 27.526 cm², 20 cm.
Example 3:
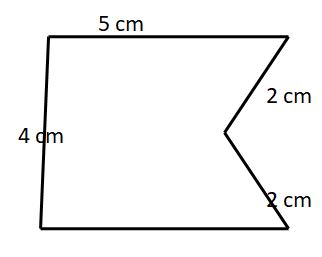
Find the perimeter, area of the below given concave polygon.
Solution:
The perimeter of the polygon = sum of all sides
= 4 + 5 + 2 + 2 + 5
= 18 cm
To find the area divide the given polygon into a square and two triangles by drawing a dotted line.
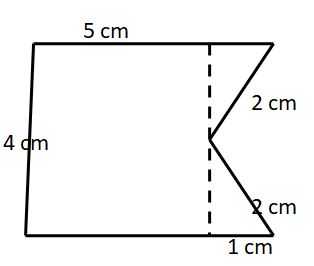
Area of square = side²
= 4² = 16 cm²
Area of triangle = 1/2 x base x height
hypotenuese² = base² + height²
2² =1² + height²
4 = 1 + h²
h² = 4 – 1
h² = 3
h = √3
So, area = 1/2 x 1 x √3
= √3/2 cm²
So, area of polygon = area of square + 2 x area of the triangle
= 16 + 2(√3/2)
= 16 + √3
Therefore, the perimeter, area of the concave polygon is 18 cm, (16 + √3) cm²
Example 4:
Find the measure of each interior, exterior angle of a regular octagon.
Solution:
Octagon has 8 sides
The sum of interior angles of polygon = (n – 2)180°
= (8 – 2) 180°
= 6 x 180°
= 1080°
The measure of each interior angle of an octagon = sum of interior angles/ number of sides
= 1080°/8
= 135°
The sum of exterior angles = 360°
The measure of each exterior angle of an octagon = sum of exterior angles/ number of sides
= 360/8
= 45°
So, the measure of each interior angle, exterior angle of the octagon is 135°, 45°. Hence, it is a convex polygon.
FAQs on Convex and Concave Polygons
1. Write the differences between concave and convex polygons?
Each and every polygon is either convex or concave. The main difference between them is angles. For a polygon to be convex, it must have all interior angles lower than 180 degrees. If any of the interior angles is greater than 180 degrees, then it is a concave polygon.
2. How do you know if a polygon is convex?
Get the measure of each interior angle of the polygon. If all the angles are below 180 degrees, then you can say it is a convex polygon.
