Big Ideas Math Answers Grade 5 Chapter 5 Multiply Decimals includes topics like Multiplication Patterns with Decimals, Multiply with Money, etc. that aid students to solve the homework and chapter practice. This will be the best and ultimate guide for exam preparation. You will find every question was explained in a simplistic way so that you are able to understand the concepts easily. Big Ideas Math Answers Grade 5 Chapter 5 Multiply Decimals pdf links are available here for each and every lesson. So, kickstart your preparation and secure the highest marks in the exams.
Big Ideas Math Book 5th Grade Answer Key Chapter 5 Multiply Decimals
Improve your Problem-Solving Skills utilizing the Big Ideas Math Book 5th Grade Answer Key Chapter 5 Multiply Decimals. Start practicing the question covered in the Big Ideas Math Answers Grade 5 Chapter 5 Multiply Decimals and Cross Check the Solutions of Chapter 5 Multiply Decimals from here. So that you can easily rectify your mistakes and fill up the knowledge gap.
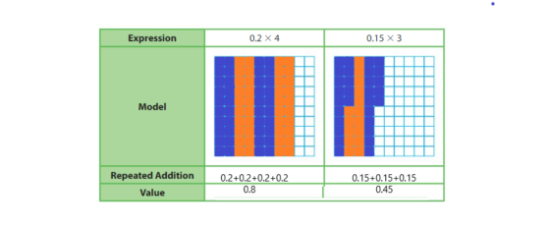
Lesson: 1 Multiplication Patterns with Decimals
- Lesson 5.1 Multiplication Patterns with Decimals
- Multiplication Patterns with Decimals Homework & Practice 5.1
Lesson: 2 Estimate Products of Decimals and Whole Numbers
- Lesson 5.2 Estimate Products of Decimals and Whole Numbers
- Estimate Products of Decimals and Whole Numbers Homework & Practice 5.2
Lesson: 3 Use Models to Multiply Decimals and Whole Numbers
- Lesson 5.3 Use Models to Multiply Decimals and Whole Numbers
- Use Models to Multiply Decimals and Whole Numbers Homework & Practice 5.3
Lesson: 4 Multiply Decimals and Whole Numbers
- Lesson 5.4 Multiply Decimals and Whole Numbers
- Multiply Decimals and Whole Numbers Homework & Practice 5.4
Lesson 5.5 Use Models to Multiply Decimals
Lesson: 6 Use Partial Products to Multiply Decimals
- Lesson 5.6 Use Partial Products to Multiply Decimals
- Use Partial Products to Multiply Decimals Homework & Practice 5.6
Lesson: 7 Use Strategies to Multiply Decimals
- Lesson 5.7 Use Strategies to Multiply Decimals
- Use Strategies to Multiply Decimals Homework & Practice 5.7
Lesson: 8 Multiply Decimals
Lesson: 9 Problem Solving: Multiply with Money
- Lesson 5.9 Problem Solving: Multiply with Money
- Problem Solving: Multiply with Money Homework & Practice 5.9
Chapter: 5 – Multiply Decimals
Lesson 5.1 Multiplication Patterns with Decimals
Explore and Grow
Use the relationship between positions in a place value chart to find each product.
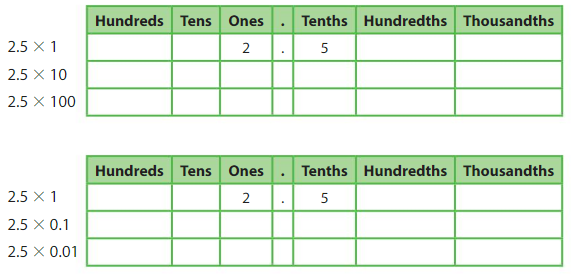
What patterns do you notice?
Answer:
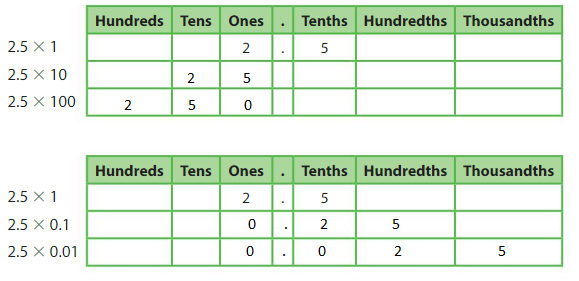
I notice that in first value chart the decimal point shifts one place to the right and in the second value chart the decimal point shifts one place to the left.
Structure
Describe the placement of the decimal point when multiplying a decimal by 10, 100, 0.1, and 0.01.
Answer:
When we multiply 0.01with 10 the decimal point shifts one place to the right(10×0.01=0.1)
When we multiply 0.01with 100 the decimal point shifts two places to the right(100×0.01=1)
When we multiply 0.01 with 0.1 the decimal point shifts one place to the left(0.1×0.01=0.001).
Think and Grow: Use Patterns to Find Products
Example
Find 0.38 × 103.
Use place value concepts. Every time you multiply a number by 10, each digit in the number shifts one position to the left in a place value chart.
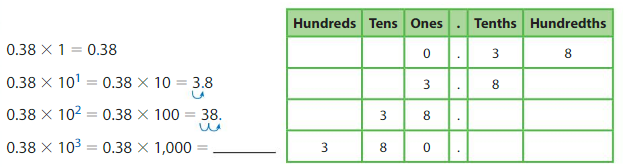
So, 0.38 × 103 = ______.
Notice the pattern: In each product, the number of places the decimal point moves to the right is the same as the exponent.
Example
Find 9.2 × 0.01.
Use place value concepts. Every time you multiply a number by \(\frac{1}{10}\) = 0.1, 10each digit in the number shifts one position to the right in a place value chart.
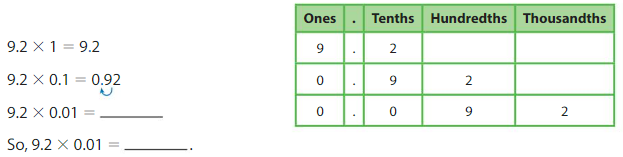
Notice the pattern: When you multiply by0.1, the decimal point moves one place to the left. When you multiply by 0.01, the decimal point moves two places to the left.
Show and Grow
Find the product.
Question 1.
2.51 × 104 = _______
Answer:
2.51×10000=25,100
Explanation:
2.51×1=2.51
2.51x 101 =2.51×10=25.1
2.51x 102 =2.51×100=251
2.51x 103 =2.51×1000=2510
2.51x 104 =2.51×10000=25100
So, 2.51x 104 =25100
When we multiply 2.51 by 104 the number of places the decimal point moves to the right is the same as the exponent ie 4 places.
Question 2.
0.7 × 0.01 = ______
Answer:
0.7 × 0.01 = 0.007
Explanation:
0.7×1=0.7
0.7×0.1=0.07
0.7×0.01=0.007
So, 0.7×0.01=0.007
When you multiply 0.7 by 0.1, the decimal point moves one place to the left. When you multiply 0.7 by 0.01, the decimal point moves two places to the left.
Apply and Grow: Practice
Find the product.
Question 3.
4.1 × 102 = _______
Answer:
4.1×100=410
Explanation:
4.1×1=4.1
4.1x 101 =4.1×10=41
4.1x 102 =4.1×100=410
So, 4.1×102 =410
When we multiply 4.1 by 102 the number of places the decimal point moves to the right is the same as the exponent ie 2.
Question 4.
7.03 × 0.1 = _______
Answer:
7.03×0.1=0.703
Explanation:
7.03×1=7.03
7.03×0.1=0.703
So, 7.03×0.1=0.703
When you multiply 7.03 by 0.1, the decimal point moves one place to the left.
Question 5.
16.579 × 104 = _______
Answer:
16.579×10000=1,65,790
Explanation:
16.579×1=16.579
16.579x 101 =16.579×10=165.79
16.579x 102 =16.579×100=1657.9
16.579x 103 =16.579×1000=16,579
16.579x 104 =16.579×10000=1,65,790
So, 16.579x 104 =1,65,790
When we multiply 16.579 by 104 the number of places the decimal point moves to the right is the same as the exponent ie 4.
Question 6.
843.7 × 0.01 = _______
Answer:
843.7×0.01=8.437
Explanation:
843.7×1=843.7
843.7×0.1=84.37
843.7×0.01=8.437
So, 843.7×0.01=8.437
When we multiply 843.7 by 0.1, the decimal point moves one place to the left.When you multiply 843.7 by 0.01, the decimal point moves two placs to the left.
Question 7.
A contractor installs a new floor of a room using 1,000 square tiles. Each tile has an area of 1.25 square feet. What is the area of the floor?

Answer:
There are 1,000 square tiles in a room, Area of each tile is 1.25 square feet
Find the area of the floor by multiplying Area of tile by Number of tiles.
Multiplying 1.25 by 1000, shifts the digits 3 positions to the left in a place value chart.So, the decimal point moves 3 places to the right.
=1.25×1000=1,250 square feet
Therefore Area of floor is 1,250 square feet.
Reasoning
complete the equation
Question 9.
_____ × 103 = 6,209
Answer:
6.209×1000=6,209
Explanation:
Multiplying something by 1000, shifts the digits 3 positions to the left in a place value chart.So, the decimal point moves 3 places to the right.As the number 6,209 is already multiplyed by 1000 now to know the missing factor shift the decimal point 3 places to the left.
So, the number is 6.209
Question 10.
_____ × 0.01 = 1.879
Answer:
187.9=0.01=1.879
Explanation:
When you multiply by 0.1, the decimal point moves one place to the left.When you multiply by 0.01, the decimal point moves two places to the left.As the number 1.879 is already multiplied by 0.01 now to know the missing factor shift the decimal point two places to the right.
So, the number is 187.9
Question 11.
0.045 × _____ = 45
Answer:
0.045×1000=45
Explanation:
0.045×1=0.045
0.045×10=0.45
0.045×100=4.5
0.045×1000=45
When we multiply 0.045 by 1000 the decimal point moves 3 placed to the right.
Think and Grow: Modeling Real Life
Example
A flea is 1.5 millimeters long. A magnified image of the flea is 100 times as long as its actual length. How much longer is the flea in the image than its actual length?

Find the length of the flea in the image by multiplying the length of the flea by 100.
Multiplying 1.5 by 100, or 102, shifts the digits _____ positions to the left in a place value chart. So, the decimal point moves ____ places to the right.
1.5 × 100 = 1.5 × 102 = ______
The length of the flea in the image is _______ millimeters.
Subtract the length of the flea from the length of the flea in the image.

The flea in the image is ________ millimeters longer than its actual length.
Answer:
Multiplying 1.5 by 100, or 102, shifts the digits right positions to the left in a place value chart. So, the decimal point moves left places to the right.
1.5 × 100 = 1.5 × 102 = 150
The length of the flea in the image is 150 millimeters.
150 – 1.5 = 148.5
The flea in the image is 148.5 millimeters longer than its actual length.
Show and Grow
Question 12.
The London Eye is a 443-foot-tall Ferris wheel. A model is 0.01 times as tall as the actual Ferris wheel. How much taller is the actual London Eye than the model?
Answer:
The London Eye is 443 feet tall Ferris, a model is 0.01 times tall as actual Ferris.
When we multiply 443 by 0.01 the decimal point moves 2 places to the left
443×0.01=4.43. So, the area of the model is 4.43 feet.
Subtract the area of the model from the actual area of the Ferris.
443.00‐ 4.43=438.57
The actual London Eye ferris wheel is 438.57 feet taller than a model ferris wheel.
Question 13.
Each day,you ride your bike from home to school and back. Your school is 0.9 mile from home. How far do you ride your bike in 10 days?
Answer:
My school is 0.9 mile from my home.If I ride bike from home to school and back every day then I ride 1.8(0.9×2) miles every day.
If each day I ride 1.8 miles then for 10 days i ride 1.8×10=18 miles.
When we multiply 1.8 by 10 and the decimal point moves 1 places to the right.
Therefore I ride 18 miles in 10 days.
Question 14.
DIG DEEPER!
An eel travels at a speed of 2 miles per hour. A starfish travels one hundredth the speed of the eel. A falcon travels 10,000 times as fast as the starfish. How many more miles per hour can the falcon travel than the eel?

Answer:
An eel travels at a speed of 2 miles per hour.A starfish and travels one hundredth the speed of the eel.
Speed of starfish is 2×0.01(one hundredth)=0.02miles per hour.
When we multiply 2 by 0.01 the decimal point moves 2 places to the left
A falcon travels 10,000 times as fast as the starfish.
Speed of falcon is 10,000×0.02(speed of starfish)=200 miles per hour.
When we multiply 0.02 by 10000 the decimal point moves 4 places to the right
A falcon can travel 200 miles more miles per hour than the eel.
Multiplication Patterns with Decimals Homework & Practice 5.1
Find the product.
Question 1.
5.201 × 10 = ______
Answer:
5.201 × 10 =52.01
Explanation:
5.201×1=5.201
5.201×10=52.01
So, 5.201×10=52.01
When we multiply 5.201 by 10 the decimal point moves one place to the right.
Question 2.
26.7 × 0.01 = _____
Answer:
26.7 × 0.01 =0.267
Explanation:
26.7×1=26.7
26.7×0.1=2.67
26.7×0.01=0.267
So, 26.7 × 0.01 =0.267
When we multiply 26.7 by 0.1, the decimal point moves one place to the left. When you multiply 26.7 by 0.01, the decimal point moves two places to the left.
Question 3.
0.095 × 103 = ______
Answer:
0.095 × 103 =0.095×1000=95
Explanation:
0.095×1=0.095
0.095x 101 =0.095×10=0.95
0.095x 102 =0.095×100=9.5
0.095x 103 =0.095×1000=95
So, 0.095 × 103 =95
When we multiply 0.095 by 103 the number of places the decimal point moves to the right is the same as the exponent ie 3 places.
Question 4.
37.84 × 0.1 = ______
Answer:
37.84 × 0.1 =3.784
Explanation:
37.84×1=37.84
37.84×0.1=3.784
So, 37.84×0.1=3.784
When we multiply 37.84 by 0.1, the decimal point moves one place to the left.
Question 5.
0.26 × 104 = ______
Answer:
0.26 × 104 =0.26×10000=2600
Explanation:
0.26×1=0.26
0.26x 101 =0.26×10=2.6
0.26x 102 =0.26×100=26
0.26x 103 =0.26×1000=260
0.26x 104 =0.26×10000=2600
So, 0.26x 104 =2600
When we multiply 0.26 by 104 the number of places the decimal point moves to the right is the same as the exponent ie 4 places.
Question 6.
15.9 × 0.01 = ______
Answer:
15.9 × 0.01 =0.159
Explanation:
15.9×1=15.9
15.9×0.1=1.59
15.9×0.01=0.159
So, 15.9×0.01=0.159
when we multiply 15.9 by 0.01 the decimal point moves two places to the left.
Find the product.
Question 7.
0.8 × 0.01 = ______
Answer:
0.8 × 0.01 =0.008
Explanation:
0.8×1=0.8
0.8×0.1=0.08
0.8×0.01=0.008
So, 0.8×0.01=0.008
When we multiply 0.8 by 0.1, the decimal point moves one place to the left. When you multiply 0.8 by 0.01, the decimal point moves two places to the left.
Question 8.
3.1 × 104 = ______
Answer:
3.1 × 104 =3.1×10000=31000
Explanation:
3.1×1=3.1
3.1x 101 =3.1×10=31
3.1x 102 =3.1×100=310
3.1x 103 =3.1×1000=3100
3.1x 104 =3.1×10000=31000
So, 3.1x 104 =31000
When we multiply 3.1 by 104 the number of places the decimal point moves to the right is the same as the exponent ie 4 places.
Question 9.
Writing
Explain how you can use mental math to find 5.4 × 103 and 5.4 × 0.01.
Answer:
5.4 × 103 and 5.4 × 0.01
5.4 × 103
5.4 × 10 × 10 × 10
= 54 × 100
= 5400
5.4 × 0.01 = 0.054
Question 10.
DIG DEEPER!
What is Newton’s number?

Answer:
Newton’s number is 49.874
Explanation:
Subtract 12.6 from 5000
5000‐12.6=4987.4
Divide the balance with 100 to find Newton’s number.
4987.4×0.01=49.874
When you multiply 4987.4 by 0.01, the decimal point moves two places to the left.
Newton’s number is 49.874
Question 11.
Modeling Real Life
A house cat weighs 9.22 pounds. Hercules the liger is the world’s largest cat, and weighs 100 times the weight of the house cat. How much more does Hercules weigh than the house cat?

Answer:
Hercules weigh 912.7 pounds more than the house cat.
Explanation:
A house cat weighs 9.22 pounds, Hercules the liger is the world’s largest cat and weighs 100 times more than a house cat.
The weight of Hercules is 9.22×100=922 pounds
When we multiply 9.22 by 100 the decimal point moves 2 places to the right.
Subtract weight of house cat from the weight of Hercules =922‐9.22=912.7
Hercules weigh 912.7 pounds more than the house cat.
Question 12.
DIG DEEPER!
A Tyrannosaurus rex weighed about 1.4 tons more than one-tenth the weight of a Patagotitan. About how much did the mayorumTyrannosaurus rex weigh?

Answer:
MayorumTyrannosaurus rex weigh=9 tons.
Explanation:
Weight of patagotitan mayorum is 76 tons and One‐tenth of patagotitan is 76×0.1=7.6 tons.
When you multiply 76.0 by 0.1 , the decimal point moves one places to the left.
A Tyrannosaurus rex weighed about 1.4 tons more than one-tenth the weight of a Patagotitan
Weight of Tyrannosaurus rex=1.4 tons + 7.6 tons= 9 tons
MayorumTyrannosaurus rex weigh=9 tons.
Review & Refresh
Question 13.
Newton and Descartes have a $50.00 gift card to a pet store. Newton’s total is $18.95 and Descartes’s total is $24.38. How much money do they have left on their gift card?
Answer:
Newton’s total is $18.95 and Descartes’s total is $24.38.
Total money they spent in a pet store =$18.95+$24.38 =$43.33
Newton and Descartes have a $50.00 gift card to a pet store
Subtract the money they spent in a pet store from the gift card money
$50.00‐$43.33=$6.67
Therefore , $6.67 is the amount they have left on their gift card.
Lesson 5.2 Estimate Products of Decimals and Whole Numbers
Explore and Grow
Choose an expression to estimate each product. Write the expression. You may use an expression more than once.
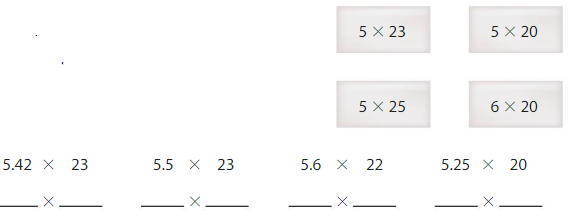
Compare your answers with a partner. Did you choose the same expressions?
Answer:
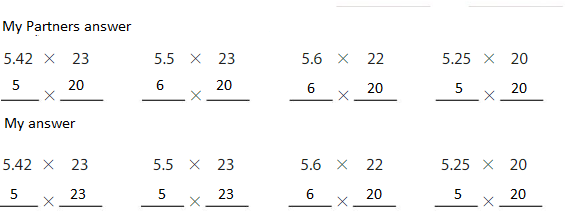
when i compared my answers with my partners answers i found that we didnot choose the same expressions.
Construct Arguments
Which estimated product do you think will be closer to the product of 2.7 and 9? Explain your reasoning.

Answer:
The estimated product of 3 and 9 is closer to the product of 2.7 and 9.
Explanation:
The product of 2.7 and 9 is 2.7×9=24.3
The product of 3 and 9 is 3×9=27
The product of 3 and 10 is 3×10=30
24.3 is closer to 27
Therefore the estimated product of 3 and 9 is closer to the product of 2.7 and 9.
Think and Grow: Estimate Products
Example
Estimate 3.85 × 27.
One Way: Use rounding. Round 3.85 to the nearest whole number. Then multiply.
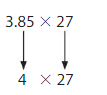
4 × 27 = ______
So, 3.85 × 27 is about = ______
Answer:
4 × 27 = 108
So, 3.85 × 27 is about = 104
Another Way: Use compatible numbers.
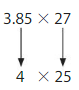
4 × 25 = ______
So, 3.85 × 27 is about = ______.
Answer:
4 × 25 = 100
So, 3.85 × 27 is about = 100.
Example
Estimate 77 × 93.6.
One Way: Use rounding. Round to the nearest ten. Then multiply.
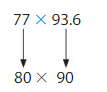
80 × 90 = _____
So, 77 × 93.6 is about = ______
Answer:
80 × 90 = 7200
So, 77 × 93.6 is about = 7200
Another Way: Use compatible numbers.
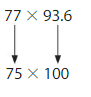
75 × 100 = _______
So, 77 × 93.6 is about = ______.
Answer:
75 × 100 = 7500
So, 77 × 93.6 is about = 7207.
Show and Grow
Estimate the product.
Question 1.
11.6 × 9
Answer:
Use rounding. Round 11.6 to the nearest whole number. Then multiply.
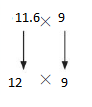
12×9=108
So, 11.6×9 is about =108
Another Way: Use compatible numbers
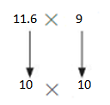
10×10=100
So, 11.6× 9 is about =100
Question 2.
159.81 × 17
Answer:
One Way: Use rounding. Round 159.81 to the nearest whole number. Then multiply.
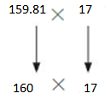
160×17=2720
So, 159.81×17 is about =2720
Another Way: Use compatible numbers
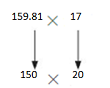
150×20=3000
So, 159.81×17 is about =3000
Apply and Grow: Practice
Estimate the product.
Question 3.
72 × 0.76
Answer:
Use rounding. Round 0.76 to the nearest whole number. Then multiply.
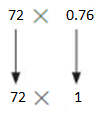
72×1 =72
So, 72×0.76 is about =72
Question 4.
6.1 × 4
Answer:
Use rounding. Round 6.1 to the nearest whole number. Then multiply.
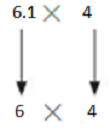
6×4=24
So, 6.1×4 is about =24
Question 5.
1.54 × 12
Answer:
Use rounding. Round 1.54 to the nearest whole number. Then multiply.
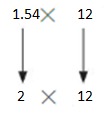
2×12=24
So, 1.54×12 is about =24
Question 6.
22 × 8.02
Answer:
Use rounding. Round 8.02 to the nearest whole number. Then multiply.
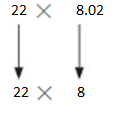
22×8=176
So, 22 × 8.02 is about = 176
Question 7.
147 × 11.6
Answer:
Use compatible numbers
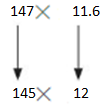
145×12=1740
So, 147×11.6 is about =1740
Question 8.
217 × 13.42
Answer:
Use compatible numbers
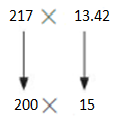
200×15=3000
So, 217×13,42 is about =3000
Question 9.
There are 1.36 liters of pineapple juice in 1 can. You buy a case of 8 cans. About how many liters of pineapple juice do you buy?

Answer:
There are 1.36 liters of pineapple juice in 1 can, there are 8 cans in a case.
Number of liters of pineapple juice in a case is about 1.36×8
Use rounding. Round 1.36 to the nearest whole number. Then multiply.
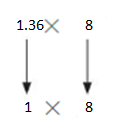
1×8=8 liters
About 8 liters of pineapple juice i shall buy.
Question 10.
Open-Ended
Write a decimal and a whole number that have an estimated product of 16.
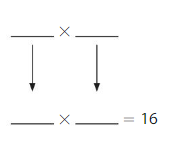
Answer:
Imagine the numbers as 1.9 and 8
1.9 × 8
Use rounding.Round 1.9 to the nearest whole number. Then multiply
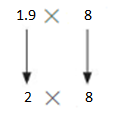
2×8=16
So, 1.9×8 is about =16.
Question 11.
Number Sense
You use 50 × 4 to estimate 45 × 3.56. Is your estimate an overestimate or an underestimate? Explain.
Answer:
My estimate is an overestimate.
Explanation:
50×4=200
45×3.56=160.2
As the product of 50 and 4 is more than the product of 45 and 3.56 so mu estimate is over estimate.
Question 12.
DIG DEEPER!
Describe a situation in which an estimate of the product of a whole number and a decimal is suffcient.
Answer:
A biscuit packet costs 4.83 rupees for a vendor and he sells 15 packets of biscuits he will earn an amount of 75 rupees(15 × 4.83=72.45).
Think and Grow: Modeling Real Life
Example
A space probe is 756,600 miles from Earth. The probe travels 9.7 miles farther from Earth each second. About how far is the space probe from Earth after 60 seconds?

Find the distance the probe travels in 60 seconds by multiplying the distance the probe travels in 1 second by60. Round 9.7 to the nearest whole number because you do not need a precise answer.
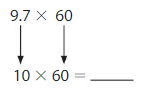
The probe travels about ______ miles in 60 seconds.
Add the distance the probe is from Earth to the distance it travels in 60 seconds.

The probe is about ______ miles from Earth after 60 seconds.
Answer:
10 × 60 = 600
The probe travels about 600 miles in 60 seconds.
Add the distance the probe is from Earth to the distance it travels in 60 seconds.
756,600 + 600 = 757200
The probe is about 757200 miles from Earth after 60 seconds.
Show and Grow
Question 13.
A bucket weighs 1.4 pounds. One gallon of sand weighs 13.4 pounds. About how much does the bucket and 4 gallons of sand weigh in all?
Answer:
A bucket weighs 1.4 pounds, A gallon of sand weighs 13.4 pounds.
Use rounding. Round 1.4 and 13.4 to the nearest whole number
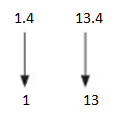
Weight of 4 gallons = 4 × weight of gallon= 4 × 13=52
The bucket and 4 gallons of sand weight=1+52=53 pounds
Question 14.
An 8.2-centimeter-tall plant grows 2.9 centimeters each month for 1 year. About how tall is the plant at the end of 1 year?
Answer:
Length of the plant now is 8.2 centimeters. If it grows about 2.9 centimeter for each month the length of the plant increased is product of 12months and the length of plant that grows each month.
Round of 8.2 and 2.9 to the nearest whole numbers
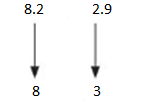
The length of the plant increased is product of 12months and the length of plant that grows each month
12×3=36
Total length= length of plant + increased length after a year=8+36 =44 centimeters
About 44 centimeters tall is the plant at the end of 1 year.
Question 15.
DIG DEEPER!
A motorcycle travels 52.3 miles using 1 gallon of gasoline. A car travels 29.8 miles using 1 gallon of gasoline. About how much farther does the motorcycle travel using 6 gallons of gasoline than the car?
Answer:
A motorcycle travels 52.3 miles using 1 gallon of gasoline and a car travels 29.8 miles using 1 gallon of gasoline
Round of 52.3 and 29.8 sto the nearest whole number.
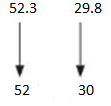
For 6 gallons of gasoline motorcycle travels 30× 6=180 miles
For 6 gallons of gasoline car travels 52× 6=312 miles
312‐180=132 miles
About 132 miles farther the motorcycle travel using 6 gallons of gasoline than the car.
Estimate Products of Decimals and Whole Numbers Homework & Practice 5.2
Estimate the product.
Question 1.
0.8 × 36
Answer:
Use rounding. Round of 0.8 to nearest whole number. And multiply
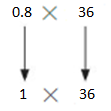
1×36=36
So, 0.8×36=36
Question 2.
2.34 × 16
Answer:
Use rounding. Round of 2.34 to the nearest whole number. And multiply
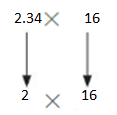
2×16=32
So, 2.34×16 is about =32
Question 3.
9 × 1.67
Answer:
Use rounding. Round of 1.67 to the nearest whole number. And multiply
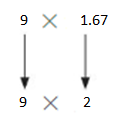
9×2=18
So, 9×1.67 is about = 18
Question 4.
105 × 4.6
Answer:
Use rounding. Round of 4.6 to the nearest whole number. And multiply
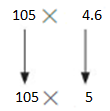
105×5=525
So, 105×4.6 is about =525
Question 5.
88 × 0.9
Answer:
Use rounding. Round of 0.9 to the nearest whole number. And multiply
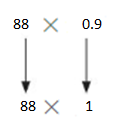
88×1=88
So, 88×0.9 is about =8
Question 6.
5.5 × 131
Answer:
Use rounding. Round of 5.5 to the nearest whole number. And multiply
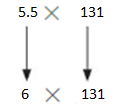
6×131=786
So, 5.5×131 is about =786
Question 7.
An athlete runs 6.23 miles in 1 hour. At this pace, about how far does the athlete run in 4 hours?
Answer:
An athlete runs 6.23 miles in 1 hour.
Use rounding.
Round of 6.23 to the nearest whole number.
6.23——6
Number of miles athlete run in 4 hours
=4× Number of miles athlete run in 1 hour
=4×6=24
About 24 miles the athlete run in 4 hours.
Question 8.
Number Sense
Which expressions are underestimates of 26.5 × 91?
20 × 90
30 × 100
30 × 90
25 × 90
Answer:
20×90 and 25×90 are the underestimates of 26.5×91 as both the estimated numbers in these expressions are less than original numbers.
Question 9.
Writing
Which strategy can you use to estimate the product of 8.02 and 106? Explain.
Answer:
I use compatible numbers strategy because numbers are near to round figures.
Question 10.
YOU BE THE TEACHER
Your friend finds the product. Is her answer reasonable? Estimate to check.?
![]()
Answer:
1.06 × 103 = 109.18
Use rounding.Round 1.06 to the nearest whole number. And multiply.
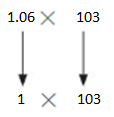
1×103 =103
So, my friend’s answer is reasonable.
Question 11.
Modeling Real Life
Newton pays for 5 pounds of pears that cost $3.75 per pound. Descartes pays$15 for 5 pounds of apples. About how much more do the 5 pounds of pears cost than the 5 pounds of apples?
Answer:
Cost of 5 pounds of pears 5×$3.75
Round 3.75 to the nearest whole number. And multiply
5×$4=$20
Descartes pays$15 for 5 pounds of apples
Subtract cost of apples from pears $20‐$15=$5
About $5 more the 5 pounds of pears cost than the 5 pounds of apples.
Question 12.
Modeling Real Life
A hospital employee works 3 days each week. The route from her house to the hospital is 9.9 miles and the route back to her house is 10.5 miles. About how many miles does she travel for work each week?
Answer:
Use rounding.Round 9.9 and 10.5 to the nearest whole numbers.
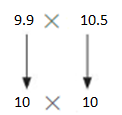
A hospital employee works 3 days each week.
So, as the route from her house to the hospital is 9.9 miles per day for 3 days it is 10×3= 30 miles
As the route back to her house is 10.5 miles per day for 3 days it is 10×3=30 miles
Total number of miles =30+30=60
Therefore About 60 miles she travel for work each week.
Review & Refresh
Question 13.
Write the number in two other forms.
Standard form:
Word form: four and twenty-six thousandths
Expanded form:
Answer:
4.26000
Lesson 5.3 Use Models to Multiply Decimals and Whole Numbers
Explore and Grow
Complete the table.
Answer:
Structure
How does the relationship between addition and multiplication help you find each product?
Answer:
Addition is the process of combining a number of individual items together to form a new total.Multiplication, however, is the process of using repeated addition and combining the total number of items that make up equal-sized groups.
Think and Grow: Use Models to Multiply Decimals and Whole Numbers
Example
Find 0.23 × 3.
Use a model. Shade 3 groups of 0.23.
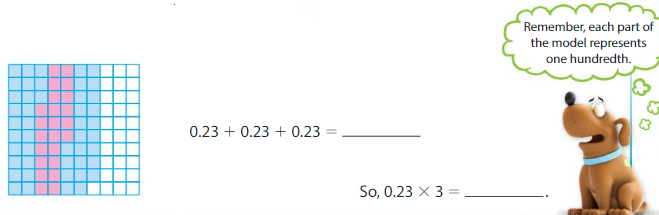
Example
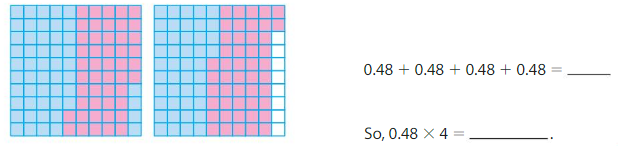
Find 0.48 × 4.
Use a model. Shade 4 groups of 0.48.
Show and Grow
Find the product.
Question 1.
0.19 × 3 = _____

Answer:
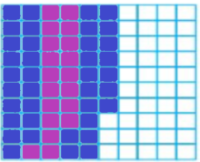
0.19+0.19+0.19=0.57
So, 0.19×3=0.57
Question 2.
0.37 × 5 = ______
Answer:

0.37+0.37+0.37+0.37+0.37=1.85
S0, 0.37×5=1.85
Apply and Grow: Practice
Find the product.
Question 3.
0.09 × 5 = _____

Answer:

0.09+0.09+0.09+0.09+0.09=0.45
So, 0.09×5=0.45
Question 4.
8 × 0.2 = _____
Answer:

0.2+0.2+0.2+0.2+0.2+0.2+0.2=1.6
So, 8×0.2=1.6
Question 5.
7 × 0.14 = _____

Answer:
0.14+0.14+0.14+0.14+0.14+0.14+0.14=0.98
So, 7×0.14=0.98
Question 6.
0.96 × 2 = _____
Answer:
0.96+0.96=1.92
So, 0.96×2=1.92
Question 7.
A hummingbird’s heart beats once every 0.05 second. How long does it take for its heart to beat 7 times?

Answer:
Given,
A hummingbird’s heart beats once every 0.05 second.
0.005 × 7 = 0.035 seconds
Question 8.
Precision
When multiplying a decimal less than one by a whole number, how does the product compare to the whole number? Is this true when multiplying two whole numbers?
Answer:
When we multiply a decimal less than one by a whole number the product will be a decimal or a whole number but when we multiply two whole numbers the product will be only a whole number.
Question 9.
DIG DEEPER!
Write two multiplication equations involving a decimal and a whole number whose product is shown.

Answer:
0.2×3=0.6 and 0.3×2=0.6
Think and Grow: Modeling Real Life
Example
You build the card tower shown. Each row is 0.08 meter tall. Your friend’s card tower is 0.3 meter tall. Whose tower is taller?

Because your card tower has 4 rows, multiply 4 by0.08 to find the height of your tower.
Use a model. Shade 4 groups of 0.08.
0.08 + 0.08 + 0.08 + 0.08 = ______
Compare the height of your tower to the height of your friend’s tower.
So, ______ tower is taller.
Answer:
0.08 + 0.08 + 0.08 + 0.08 = 0.32
Compare the height of your tower to the height of your friend’s tower.
So, 0.32tower is taller.
Show and Grow
Question 10.
You have 1 meter of ribbon. Do you have enough ribbon to border the outside of the square picture frame?

Answer:
No
Explanation:
Length of side of the square picture is 0.33m.
Border of the square picture is 4 × length of side=4×0.33m=1.32m
I have 1 meter of ribbon 1.32>1
So, i don’t have enough ribbon to border the square picture.
Question 11.
Organic shaved coconut originally costs $0.34 per ounce. A baker buys 8 ounces on sale for $0.27 per ounce.How much money does the baker save?

Answer:
Money the baker save is 0$2.72‐$2.16=$0.56
Explanation:
Original cost of organic shaved coconut is $0.34 per ounce
Then for 8 ounces it will be 8×$0.34=$2.72
Cost of the baker is $0.27 per ounce
Then for 8 ounces it will be 8×$0.27=$2.16
Money the baker save is 0$2.72‐$2.16=$0.56
Question 12.
DIG DEEPER!
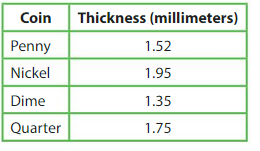
You have 4 pennies, 3 nickels, and 2 quarters. Find the total weight and the total value of your coins.

Answer:
4 × 2.5 = 10
3 × 5 = 15
2 × 5.67 = 11.34
10 + 15 + 11.34 = 36.34
Use Models to Multiply Decimals and Whole Numbers Homework & Practice 5.3
Find the product.
Question 1.
0.4 × 2 = _____

Answer:
0.4+0.4=0.8
So, 0.4×2=0.84
Question 2.
6 × 0.31 = _____
Answer:
0.31+0.31+0.31+0.31+0.31+0.31=1.86
So, 6×0.31=1.86
Question 3.
0.54 × 3 = _____
Answer:
0.54+0.54+0.54=1.62
So, 0.54×3=1.62
Question 4.
0.25 × 7 = _____
Answer:

0.25+0.25+0.25+0.25+0.25+0.25+0.25=1.75
So, 0.25×7=1.75
Find the product
Question 5.
0.22 × 4 = _____

Answer:
0.22+0.22+0.22+0.22=0.88
So, 0.22×4=0.88
Question 6.
5 × 0.4 = _____
Answer:
0.4+0.4+0.4+0.4+0.4=2
So, 5×0.4=2
Question 7.
A city mayor plans to build two new parks. Each park will cover 1.45 acres. How many acres will the new parks cover altogether? Explain.
Answer:
2.9 Acers
Explanation:
Acres covered by one park is 1.45 acres, A city mayor plans to build two new parks.
Acres covered by two new parks is 2×1.45=2.9acers.
Question 8.
Structure
Write an equation represented by the model.
Answer:
0.35+0.35+0.35+0.35+0.35=1.75
So, 0.35×5=1.75
Question 9.
DIG DEEPER!
Find the product of 0.03 and 4. How does the product change when you replace 4 with 0.4? Explain.
Answer:
The product of 0.03 and 4 is 0.03×4=0.12
The product of 0.03 and 0.4 is 0.03×0.4=0.012
When we replace the 4 with 0.4 then the product will become very small.
Question 10.
Modeling Real Life
In 1 year, you spend $1.50 on electricity to charge your tablet. In 1 month, you spend $0.02 on electricity to charge your smart phone. Which device costs more to charge in 1 year?
Answer:
In 1 year, i spend $1.50 on electricity to charge my tablet
If In 1 month, i spend $0.02 on electricity to charge my smart phone in a year i spend = 12months × electricity charge per month
=12×0.02=$0.24
$0.24<$1.50
Therefore Tablet costs more to charge in 1 year.
Question 11.
DIG DEEPER!
You have a 2-pound carton of blueberries. You eat 0.2 of the carton on Monday and 0.35 of the carton on Tuesday. How many pounds of blueberries are left?
Answer:
Weight of carton of blueberries is 2 pounds
I ate 0.2 of carton on Monday 0.2×2=0.4 pounds
I ate 0.35 of carton on Tuesday 0.35×2=0.7
Total of berries i ate is 0.4+0.7=1.1
pounds of blueberries are left=2‐1.1=0.9
Therefore 0.9 pounds of blueberries are left in the carton.
Review & Refresh
Evaluate the expression.
Question 12.
(12 ÷ 4) × 30 – 15
Answer:
(12 ÷ 4) × 30 – 15=75
Explanation:
(12 ÷ 4) × 30 – 15
=(3)×30‐15
=90‐15
=75
S0, (12 ÷ 4) × 30 – 15=75
Question 13.
(11 + 7) ÷ (3 + 5 + 1)
Answer:
(11 + 7) ÷ (3 + 5 + 1)=2
Explanation:
(11 + 7) ÷ (3 + 5 + 1)
=(18)÷(9)
=2
So, (11 + 7) ÷ (3 + 5 + 1)=2
Question 14.
35 ÷ [(153 – 139) ÷ 2]
Answer:
35 ÷ [(153 – 139) ÷ 2]=5
Explanation:
35 ÷ [(153 – 139) ÷ 2]
=35÷[(14÷2)]
=35÷7
=5
So, 35 ÷ [(153 – 139) ÷ 2]=5
Lesson 5.4 Multiply Decimals and Whole Numbers
Explore and Grow
Complete the table.

What pattern do you notice in the placement of the decimal point?
Answer:

We can notice that the decimal point moves one place to the left.
Structure
How is multiplying decimals similar to multiplying whole numbers?
Answer:
Decimal multiplication is similar to the multiplication of whole numbers after decimal point the product of the numbers is the same.
Think and Grow: Multiply a Decimals and a Whole Numbers
Example
Find 5.8 × 4. Estimate ________
One Way: Multiply as you do with whole numbers. Then place the decimal point.
Find 58 × 4.

Another Way: Use place value and partial products.
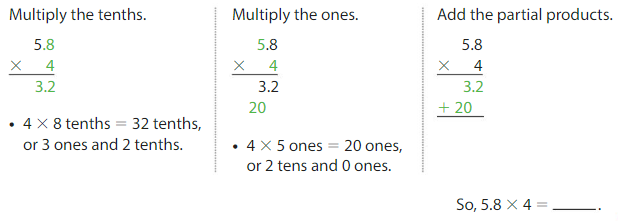
So, 5.8 × 4 = ______.
Show and Grow
Find the product. Check whether your answer is reasonable.
Question 1.
2.4 × 7 = ______
Answer:
2.4 × 7 =16.8
Explanation:
2.4 × 7
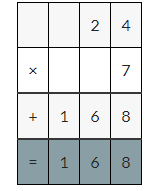
Multiply 24 with 7
24×7=168
Multiply 168 with 0.1
168×0.1=16.8 decimal point moves one place to the left.
So, 2.4 × 7 =16.8
Question 2.
8.15 × 3 = ______
Answer:
8.15 × 3 =24.45
Explanation:
8.15 × 3
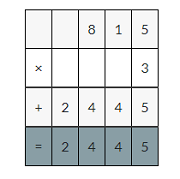
Multiply 8.15 with 3
815×4=2445
Multiply 2445 with 0.01
2445×0.01=24.45 decimal point moves two places to the left.
So, 8.15 × 3 =24.45
Apply and Grow: Practice
Find the product.
Question 3.
6 × 5.3 = _____
Answer:
6×5.3=31.8
Explanation:
6×5.3=
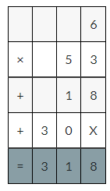
6×53=318
318 ×0.1=31.8decimal point moves one place to the left.
So,6 ×5.3=31.8
Question 4.
4.68 × 4 = ______
Answer:
4.68×4=18.72
Explanation:
4.68×4
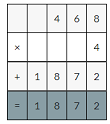
468×4=1872
1872×0.01=18.72decimal point moves two places to the left.
So, 4.68 × 4 =18.72
Question 5.
7 × 0.81 = ______
Answer:
7×0.81=5.56
Explanation:
7×0.81
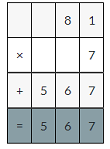
7×81=567
567×0.01=5.67decimal point moves two places to the left.
So, 7 × 0.81 =5.67
Question 6.
1.45 × 5 = _____
Answer:
1.45 × 5=7.25
Explanation:
1.45 × 5
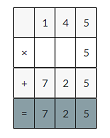
145×5=725
725×0.01=7.25decimal point moves two places to the left.
So, 1.45 × 5 =7.25
Question 7.
34 × 7.2 = _____
Answer:
34 × 7.2=244.8
Explanation:
34 × 7.2
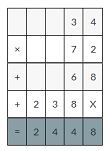
34×72=2448
2448×0.1=244.8decimal point moves one place to the left.
So, 34 × 7.2=244.8
Question 8.
23.66 × 19 = ______
Answer:
23.66 × 19=499.54
Explanation:
23.66 × 19
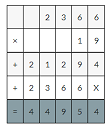
2366×19=44954
44954×0.01=449.54decimal point moves two places to the left.
So, 23.66 × 19 =449.54
Question 9.
How much do you pay for 3 pounds of grapes?

Answer:
One pound of grapes costs $1.98
3 pounds of grapes cost is 3×$1.98
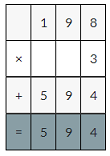
=3×198=598
598×0.01=5.98decimal point moves two places to the left.
Therefore cost of 3 pounds of grapes is 5.98
Question 10.
Which One Doesn’t Belong?
Which equation is not true?

Answer:
0.4×15=60 is not correct
Explanation:
0.4×15
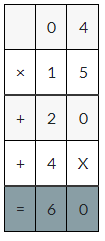
4×15=60
60×0.1=6decimal point moves one place to the left.
0.4×15=6
Therefore it is a wrong equation.
Question 11.
Number Sense
Without calculating, determine whether the product of 0.67 and 8 is greater than or less than 8. Explain.
Answer:
The product of 0.67 and 8 is less than 8.
Explanation:
We know that 0.67 is less than 1 so 0.67 when multiplied with 8 will be less than 8.
Question 12.
DIG DEEPER!
Find the missing digits. Then find the product.
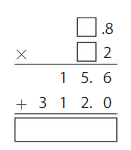
Answer:
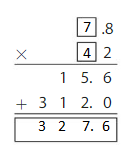
Think and Grow: Modeling Real Life
Example
You buy a 40-pack of bottled water. Each bottle contains 16.9 fluid ounces of water. You drink 10 bottles. How many total fluid ounces of water do you have left?

Subtract 10 from the number of bottles you buy to find the number of bottles you have left.
40 – 10 = 30
To find how much water you have left, multiply the number of bottles you have left by16.9. Multiply as you do with whole numbers. Then place the decimal point.

You have _______ total fluid ounces of water left.
Show and Grow
Question 13.
The stories of a residential building are 3.2 meters tall. The stories of an office building are 0.4 meter taller than the stories in the residential building. The office building has 12 stories. How tall is the office building?
Answer:
The stories of a residential building are 3.2 meters tall.The stories of an office building are 0.4 meter taller than the stories in the residential building
So stories of office building is 3.2+0.4=3.6 meter tall
Office building has 12 stories and each storey is 3.6 meters tall
So, 12×3.6=
12×36=432
432×0.1=43.2decimal point moves one place to the left.
Therefore the office building is 43.2 meters tall.
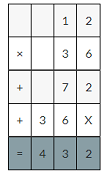
Question 14.
You have3 strands of lights that are each 10.8 feet long. You buy 5 strands of lights that are each 16.25 feet long. How many feet of lights do you have in all?
Answer:
If i have3 strands of lights that are each 10.8 feet long
The length of 3 strands is 3×10.8
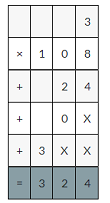
3×10.8=324×0.1 = 32.4 feet decimal point moves one place to the left.
If i buy 5 strands of lights that are each 16.25 feet long
The length of 5 strands is 5×16.25
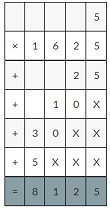
5×1625=8125
1825×0.01=81.25decimal point moves two places to the left.
Feet of lights i have in all is32.4+81.25=133.65 feet.
Question 15.
DIG DEEPER!
You stack $1 in dimes and you stack $1 in quarters. Which stack is taller? How much taller?
Answer:
1.35 × 1 = 1.35
1.75 × 1 = 1.75
Multiply Decimals and Whole Numbers Homework & Practice 5.4
Find the product.
Question 1.
9.8 × 2 = _____
Answer:
9.8×2=19.6
Explanation:
9.8×2
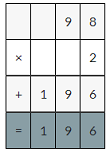
98×2=196
196×0.1=19.6 decimal point moves one place to the left.
So, 9.8×2=19.6
Question 2.
0.61 × 8 = ______
Answer:
0.61 × 8 =4.88
Explanation:
0.61×8
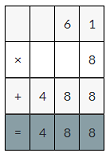
61×8=488
488×0.01=4.88decimal point moves two places to the left.
So, 0.61 × 8 =4.88
Question 3.
82 × 1.1 = ______
Answer:
82×1.1=90.2
Explanation:
82×1.1
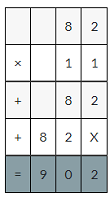
82×11=902
902×0.1=90.2decimal point moves one place to the left.
So, 82×1.1=90.2
Question 4.
43 × 0.6 = ______
Answer:
43×0.6=25.8
Explanation:
43×0.6
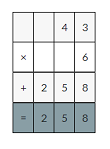
43×6=258
258×0.1=25.8decimal point moves one place to the left.
So, 43×0.6=25.8
Question 5.
2.39 × 57 = _______
Answer:
2.39×57=136.23
Explanation:
2.39×57
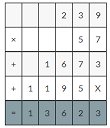
239×57=13623
13623×0.01=136.23decimal point moves two places to the left.
So, 2.39×57=136.23
Question 6.
10.75 × 24 = ______
Answer:
10.75×24=258
Explanation:
10.75×24
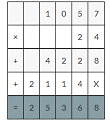
1075×24=25800
25800×0.01=258.00=258decimal point moves two places to the left.
So, 10.75×24=258
Question 7.
There are 6.3 grams of protein in a boiled egg. You eat 3 boiled eggs. How many grams of protein do you consume?
Answer:
There are 6.3 grams of protein in a boiled egg
I eat 3 boiled eggs and grams of protein i consumed=3×6.3
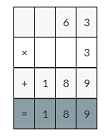
3×63=189
189×0.1=18.9decimal point moves one place to the left.
Therefore 18.9 grams of protein i consumed.
Question 8.
Reasoning
Newton says the product of 7.55 and 8 is 60.40. Descartes says the product is 60.4.Who is correct? Explain.
Answer:
Both Newton’s and Descartes answers are correct as zero at the end of a number after decimal point does not change the value of the number 60.40 and 60.4 is same.
Question 9.
Patterns
Describe and complete the pattern.
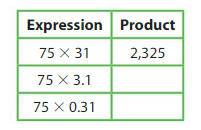
Answer
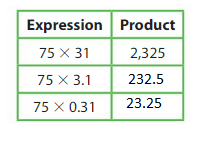
In the above table the decimal point is shifting one place to the left in each expression respectively.
Question 10.
YOU BE THE TEACHER
Your friend finds 14 × 0.82. Is your friend correct? Explain.
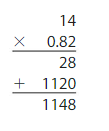
Answer:
My friend is incorrect.
Explanation:
14×0.82
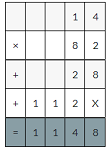
14×82=1148
1148×0.01=11.48decimal point moves two places to the left.
14×0.82=11.48.
so, my friends answer is correct.
Question 11.
Modeling Real Life
A person weighs 2.34 times as much on Jupiter as on Earth. An 85-pound student would weigh 90.1 pounds less on Saturn than on Jupiter. How much would he weigh on Saturn?
Answer:
85 pounds student weighs 2.34 times as much on Jupiter as on Earth.So, weight on jupiter is 85×2.34
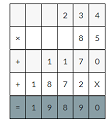
85×234=19890
19890×0.01=198.90decimal point moves two places to the left.
Weight on jupiter is 198.9
student would weigh 90.1 pounds less on Saturn than on Jupiter
So, weight on saturn = weight on Jupiter ‐ 90.1=198.9‐90.1=108.8
Therefore An 85-pound student would weigh 108.8 on saturn.
Question 12.
DIG DEEPER!
A landscaper digs a rectangular region for a garden. The length is a one-digit whole number of meters. What is the least possible area? What is the greatest possible area?

Answer:
If length of rectangular region is a one-digit whole number of meters and breadth is 4.75 meters.
Smallest 1 digit whole number is 1
The least possible area is 1×4.75 =4.75 squaremeters
Largest 1 digit whole number is 9
The greatest possible area is 9×4.75
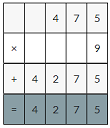
9×475=4275
4275×0.01=42.75 square meters decimal point moves two places to the left.
Therefore The least possible area and the greatest possible area is 4.75 and 42.75 square meters respectively.
Review & Refresh
Find the sum or difference.
Question 13.
0.83 – 0.14 = ______
Answer:
0.83 – 0.14=0.96
Explanation:
0.83‐0.14=
83‐14=69
69×0.01=0.69decimal point moves two places to the left.
So, 0.83 – 0.14=0.96
Question 14.
1.34 + 1.35 = _______
Answer:
1.34 + 1.35 =2.69
Explanation:
1.34 + 1.35
134+135=269
269×0.01=2.69decimal point moves two places to the left.
So, 1.34 + 1.35 =2.69
Lesson 5.5 Use Models to Multiply Decimals
Explore and Grow
A rectangle is 0.8 meter long and 0.7 meter wide.
Use a model to find the area of the rectangle.

Answer:
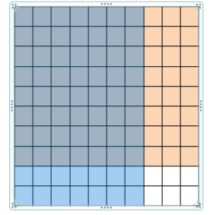
Use a model to find 0.8 × 0.7
Use a model. Shade 8 rows to represent 0.8 and shade 7 columns to represent 0.7
56 squares are shaded twice
So, 0.8 × 0.7=0.56
Use a model to find 0.8 × 1.7.
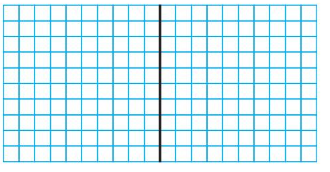
Answer:
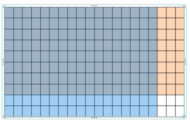
Use a model to find 0.8 × 1.7
Use a model. Shade 8 rows to represent 0.8 and shade 17 columns to represent 1.7
136 squares are shaded twice
So, 0.8 × 1.7 =1.36
Reasoning
When using a model to multiply decimals, how do you determine the number of rows and columns to shade?
Answer:
For a given multiplication of decimals. The multiplyer is used to determine the number of rows and the multiplicand is used to determine the number of columns.
Think and Grow: Use Models to Multiply Decimals
Example
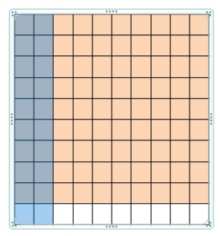
Use a model to find 0.4 × 0.6
Use a model. Shade 4 rows to represent 0.4 and shade 6 columns to represent 0.6.
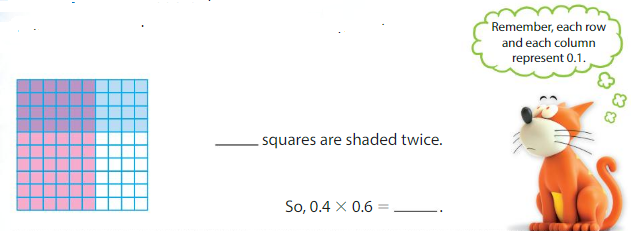
Example
Use a model to find 0.7 × 1.4.
Use a model. Shade 7 rows to represent 0.7 and shade 14 columns to represent 1.4.
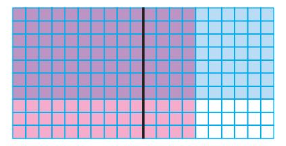
_____ squares are shaded twice.
So, 0.7 × 1.4 = ______.
Show and Grow
Use the model to find the product.
Question 1.
0.9 × 0.2 = _____

Answer:
Use a model to find 0.9 × 0.2
Use a model. Shade 9 rows to represent 0.9 and shade 2 columns to represent 0.2
18 squares are shaded twice
So, 0.9 × 0.2 =0.18
Question 2.
0.8 × 1.5 = ______

Answer:
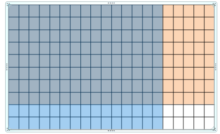
Use a model to find 0.8 × 1.5
Use a model. Shade 8 rows to represent 0.8 and shade 15 columns to represent 1.5
120 squares are shaded twice
So, 0.8 × 1.5 =1.2
Apply and Grow: Practice
Use the model to find the product.
Question 3.
0.4 × 0.4 = ______

Answer:
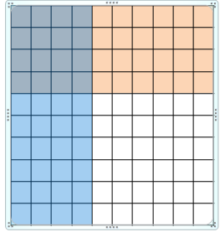
Use a model to find 0.4 × 0.4
Use a model. Shade 4 rows to represent 0.4 and shade 4 columns to represent 0.4
16 squares are shaded twice
So, 0.4 × 0.4 =0.16
Question 4.
0.9 × 0.9 = _______

Answer:
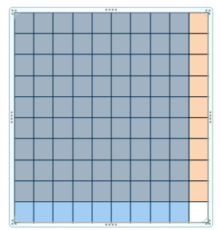
Use a model to find 0.9 × 0.9
Use a model. Shade 9 rows to represent 0.9 and shade 9 columns to represent 0.9
81 squares are shaded twice
So, 0.9 × 0.9 =0.81
Question 5.
0.2 × 1.7 = ____
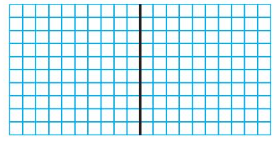
Answer:
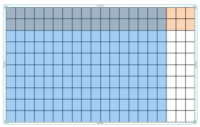
Use a model to find 0.2 × 1.7
Use a model. Shade 2 rows to represent 0.2 and shade 17 columns to represent 1.7
34 squares are shaded twice
So, 0.2 × 1.7 =0.34
Question 6.
0.6 × 1.6 = _______
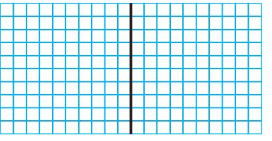
Answer:
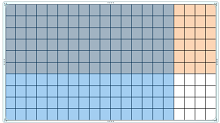
Use a model to find 0.6 × 1.6
Use a model. Shade 6 rows to represent 0.6 and shade 16 columns to represent 1.6
96 squares are shaded twice
So, 0.6× 1.6 =0.96
Question 7.
On Saturday, you ride your bike 1.5 miles. On Sunday, you ride your bike 0.7 times as far as you did on Saturday. How far do you ride your bike on Sunday?
Answer:
On saturday i rode my bike for 1.5 miles
On sunday i rode 0.7 times as far as i did on saturday
miles i rode bike on sunday =0.7×1.5=1.05
Therefore, 1.05miles far i rode my bike on sunday.
Question 8.
Reasoning
When multiplying 0.4 × 0.3, why is the product less than each of the factors?
Answer:
When we multiply 0.4 with 0.3 the product is less than each of their factors this is because we are finding a fractional amount of a quantity.
Question 9.
DIG DEEPER!
Shade the model to represent the product of 0.6 and 0. What is the product? Explain.

Answer:
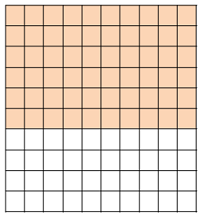
Use a model to find 0.6 × 0
Use a model. Shade 6 rows to represent 0.6 and shade 0 columns to represent 0
No squares are shaded twice
So, 0.6× 0=0
Think and Grow: Modeling Real Life
Example
A donkey is 0.9 meter tall. A horse is 1.7 times as tall as the donkey. How much taller is the horse than the donkey?

Multiply 0.9 by 1.7 to find the height of the horse.
Use a model. Shade 9 rows to represent 0.9 and shade 17 columns to represent 1.7.
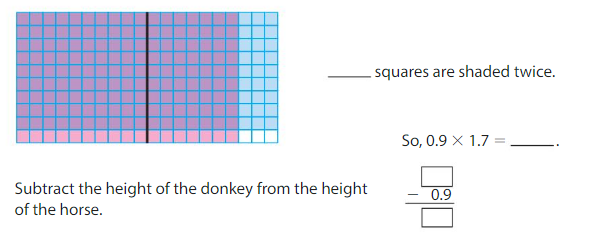
So, the horse is ______ meter taller than the donkey.
Answer:
0.9 × 1.7 = 1.53
1.53 squares are shaded twice.
1.53 – 0.9 = 0.63
So, the horse is 0.63 meter taller than the donkey.
Show and Grow
Question 10.
On Sunday, you run 0.6 mile. On Monday, you run 1.3 times as far as you run on Sunday. How many more miles do you run on Monday than on Sunday?
Answer:
Multiply 0.6 by 1.3 to find the number of miles i run on monday.
usinga model. Shade 6 rows to represent 0.6 and shade 13 columns to represent 1.3.
78 squares are shaded twice.
So, i ran 0.78 miles on monday.
Subtract the number of miles i ran on monday from the miles i ran on sunday.
0.78‐0.6=0.72
Therefore 0.72miles i ran on Monday than on Sunday
Question 11.
A candle burns 0.2 ounce of wax each hour. A candle with 14.5 ounces of wax burns for 2.5 hours. How much wax is left?
Answer:
A candle with 14.5 ounces of wax burns for 2.5 hours and a candle burns 0.2 ounce of wax each hour.
Ounces of wax burnt in 2.5 hours is
2.5 hours × ounces of wax burns in each hour.
2.5×0.2=0.5 ounces
Ounced of Wax left=14.5‐0.5=14 ounces.
Question 12.
DIG DEEPER!
You have a bottle that contains 1.5 liters of apple juice. You drink 0.2 of the bottle on Friday, and 0.3 of the juice remaining in the bottle on Saturday. How much apple juice do you have left?

Answer:
A bottle contains 1.5 liters of apple juice.
If i drink 0.2 of the bottle on Friday the amount of juice left is 1.5‐(1.5×0.2)=1.5 ‐ 0.3= 1.2
If i drink 0.3 of the juice remaining in the bottle on Saturday the amount of juice left is
=1.2‐(1.2×0.3)=1.2 ‐ 0.36= 0.84
Apple juice i have left id 0.84 liters.
Use Models to Multiply Decimals Homework & Practice 5.5
Use the model to find the product.
Question 1.
0.8 × 0.9 = ______

Answer:
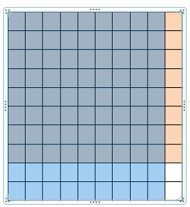
Use a model to find 0.8 × 0.9
Use a model. Shade 8 rows to represent 0.8 and shade 9 columns to represent 0.9
72 squares are shaded twice
So, 0.8 × 0.9 =0.72
Question 2.
0.4 × 0.2 = _____

Answer:
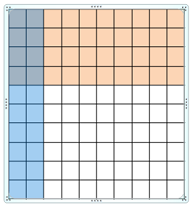
Use a model to find 0.4 × 0.2
Use a model. Shade 4 rows to represent 0.4 and shade 2 columns to represent 0.2
8 squares are shaded twice
So, 0.4 × 0.2 =0.08
Question 3.
0.6 × 1.9 = ______
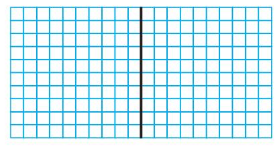
Answer:
Use a model to find 0.6 × 1.9
Use a model. Shade 6 rows to represent 0.6 and shade 19 columns to represent 1.9
114 squares are shaded twice
So, 0.6 × 1.9 =1.14
Question 4.
0.7 × 1.2 = ______
Answer:
Use a model to find 0.7 × 1.2
Use a model. Shade 7 rows to represent 0.7 and shade 12 columns to represent 1.2
84 squares are shaded twice
So, 0.7 × 1.2 =0.84
Question 5.
One banana contains 1.3 grams of protein. How much protein is in 0.5 of a banana?
Answer:
One banana contains 1.3 grams of protein
0.5 of a banana contains 1.3×0.5=0.65 grans of proteins.
Question 6.
Reasoning
When multiplying 0.6 and 1.2, why is the product less than only one of the factors?
Answer:
When multiplying 0.6 and 1.2, the product less than only one of the factors because we are finding a fractional amount of a quantity a part of the number.
Question 7.
YOU BE THE TEACHER
Newton says that 0.2 × 0.2 = 0.36, because there are 36 squares shaded. Is he correct? Explain.
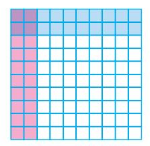
Answer:
No
Explanation:
No, Newton’s answer is not correct as the number of squares shaded twice are 4 so, the product will be 0.4 not 0.36.
Question 8.
Structure
Write a multiplication equation that is represented by the model.

Answer:
Number of rows shaded are 6 so, the decimal is 0.6
Number of columns shaded are 7 so, the decimal is 0.7
Number of squares shaded twice are 42 so, the product is 0.42
Therefore multiplication equation is 0.6×0.7=0.42.
Question 9.
Modeling Real Life
A pancake batter recipe calls for 0.5 cup of water. The recipe calls for 1.5 times as much pancake mix as water.How much more pancake mix is needed than water?

Answer:
A pancake batter recipe calls for 0.5 cup of water.
The recipe calls for 1.5 times as much pancake mix as water
Amount of pancake mix is 0.5×1.5=0.75 cups
Subtract the amount of pancake mix from the amount of water
0.75‐0.5=0.70 cups
Therefore 0.70 cups more pancake mix is needed than water.
Question 10.
DIG DEEPER!
To make crafts, you buy colored paper for $1.90. You buy a pack of googly eyes that costs 0.4 times as much as the colored paper. How much money do you spend in all?

Answer:
Cost of colored paper is $1.90
Cost of a pack of googly eyes is 0.4 times as much as the colored paper=0.4×1.90=$0.76
Add the money spent on colored paper and on googly eyes=$1.90+$0.76=$2.66
The money i spent in all is $2.66.
Review & Refresh
Write the value of the underlined digit.
Question 11.
5,120,379
Answer:
5,120,379
Value of 1 in the above number is 1 Hundred Thousands
Question 12.
400,681
Answer:
400,681
Value of 6 in the above number is 6 hundred.
Question 13.
7,245,819
Answer:
7,245,819
Value of 7 in the above number is 7 million.
Question 14.
23, 504
Answer:
23, 504
Value of 2 in the above number is 2 Ten Thousands
Lesson 5.6 Use Partial Products to Multiply Decimals
Explore and Grow
Use the area model and partial products to find 1.4 × 1.5.
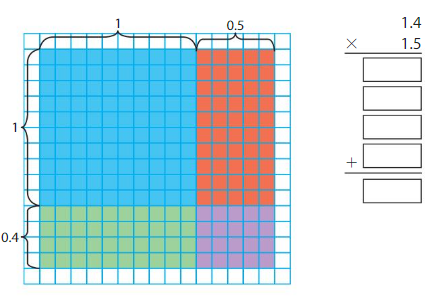
Answer:
From the above grid we can note down the following expressions
1×1
1×0.4
1×0.5
0.4×0.5
Find the product of the four equations and then add their products to find the area of the model
1×1=1
1×0.4=0.4
1×0.5=0.5
0.4×0.5=0.2
Add the products of the above four equations
1+0.4+0.5+0.2=2.1
Structure
How can you use partial products to multiply decimals?
Answer:
Breaking up the number to multiply into parts, multiplying the parts separately, and then adding is called partial product.we can use partial product strategy to find the product of decimals by breaking them into parts.
Think and Grow: Use Partial Products toMultiply
Example
Use partial products to find 3.2 × 4.8. Estimate ________

Show and Grow
Find the product. Check whether your answer is reasonable.
Question 1.
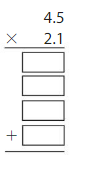
Answer:
4.5×2.1
1.Multiply the tenths by tenths =0.5×0.1=0.05
2.Multiply the ones by tenths = 0.5×2=1
3.Multiply the tenths by ones = 4×0.1=0.4
4.Multiply the ones by ones =4×2=8
Add all the partial products =0.05+1+0.4+8=9.45
Therefore 4.5×2.1=9.45
Question 2.
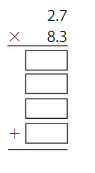
Answer:
2.7×5.3
1.Multiply the tenths by tenths =0.7×0.3=0.21
2.Multiply the ones by tenths = 0.3×2=0.6
3.Multiply the tenths by ones = 5×0.7=3.5
4.Multiply the ones by ones =5×2=10
Add all the partial products =0.21+0.6+3.5+10=14.31
Therefore 2.7×5.3=14.31
Question 3.
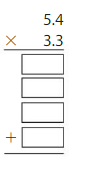
Answer:
5.4×3.3
1.Multiply the tenths by tenths =0.3×0.4=0.12
2.Multiply the ones by tenths = 0.3×5=1.5
3.Multiply the tenths by ones = 4×0.3=1.2
4.Multiply the ones by ones =5×3=15
Add all the partial products=0.12+1.5+1.2+15=17.82
Therefore 5.4×3.3=17.82
Apply and Grow: Practice
Find the product. Check whether your answer is reasonable.
Question 4.
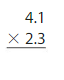
Answer:
4.1×2.3
1.Multiply the tenths by tenths =0.1×0.3=0.03
2.Multiply the ones by tenths = 0.1×2=0.2
3.Multiply the tenths by ones = 4×0.3=1.2
4.Multiply the ones by ones =4×2=8
Add all the partial products=0.03+0.2+1.2+8=9.43
Therefore 4.1×2.3=9.43
Question 5.
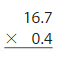
Answer:
16.7×0.4
1.Multiply the tenths by tenths =0.7×0.4=0.28
2.Multiply the ones by tenths = 0.7×0=0
3.Multiply the tenths by ones = 16×0.4=6.4
4.Multiply the ones by ones =16×0=0
Add all the partial products=0.28+6.4=6.68
Therefore 16.7×0.4=6.68
Question 6.
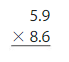
Answer:
5.9×8.6
1.Multiply the tenths by tenths =0.9×0.6=0.54
2.Multiply the ones by tenths = 0.9×8=7.23.
Multiply the tenths by ones = 5×0.6=3
4.Multiply the ones by ones =5×8=40
Add all the partial products=0.54+7.2+3+40=50.74
Therefore 5.9×8.6=50.74
Question 7.
23.7 × 3.5 = ______
Answer:
23.7×3.5
1.Multiply the tenths by tenths =0.7×0.5=0.35
2.Multiply the ones by tenths = 0.7×3=2.1
3.Multiply the tenths by ones = 23×0.5=11.5
4.Multiply the ones by ones =23×3=69
Add all the partial products=0.35+2.1+11.5+69=82.95
Therefore 23.7×3.5=82.95
Question 8.
10.6 × 14.7 = ______
Answer:
10.6×14.7
1.Multiply the tenths by tenths =0.6×0.7=0.42
2.Multiply the ones by tenths = 0.6×14=8.4
3.Multiply the tenths by ones = 10×0.7=7
4.Multiply the ones by ones =10×14=140
Add all the partial products=0.42+8.4+9.8+140=155.82
Therefore 10.6×14.7=155.82
Question 9.
1.2 × 3.71 = ______
Answer:
1.2×3.71
1.Multiply the tenths by tenths =0.2×0.71=0.142
2.Multiply the ones by tenths = 0.2×3=0.6
3.Multiply the tenths by ones = 1×0.71=0.71
4.Multiply the ones by ones =1×3=3
Add all the partial products=0.142+0.6+0.71+3=4.452
Therefore 1.2×3.71=4.452
Question 10.
A space probe travels 643.5 miles every minute. How far does it travel in 1.5 minutes?

Answer:
A space probe travels 643.5 miles every minute.
The distance it travel in 1.5 minutes is 643.5×1.5
643.5×1.5
1.Multiply the tenths by tenths =0.5×0.5=0.25
2.Multiply the ones by tenths = 0.5×1=0.5
3.Multiply the tenths by ones = 643×0.5=321.5
4.Multiply the ones by ones =643×1=643
Add all the partial products is=0.25+0.5+321.5+643=965.25
Therefore 643.5×1.5=965.25
Question 11.
Number Sense
Which products are greater than 20.4?
3.4 × 7.2
2.5 × 4.8
3.2 × 6.3
8.6 × 2.4
Answer:
3.4 × 7.2=24.48>20.4
2.5 × 4.8=12<20.4
3.2 × 6.3=20.16<20.4
8.6 × 2.4=2.64>20.4
The products of 3.4×7.2 and 8.6×2.4 are greater than 20.4.
Question 12.
Precision
How can you use estimation to help you place the decimal point in a product? Explain.
Answer:
You will need to multiply and then estimate the solution. Start by multiplying just as if you are multiplying whole numbers. Because the original numbers have 4 digits total after their decimal points , insert a decimal point into your answer so that it has 4 digits to its right.
Question 13.
DIG DEEPER!
Write a multiplication equation shown by the partial products.
0.14 + 0.2 + 2.1 + 3
Answer:
0.14 + 0.2 + 2.1 + 3 = 5.44
Think and Grow: Modeling Real Life
Example
A geologist has a blue geode that weighs 2.5 pounds. The geologist has a purple geode that weighs 1.6 times as much as the blue geode. What is the total weight of the geodes?
Find the weight of the purple geode by multiplying the weight of the blue geode by 1.6
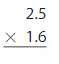
The weight of the purple geode is ______ pounds.
Add the weights of the blue geode and the purple geode.
The total weight of the geodes is ______ pounds.
Show and Grow
Question 14.
You buy 3.5 yards of yellow fabric to make a Chinese dragon. You buy 2.5 times as much red fabric as yellow fabric. How many yards of fabric do you buy in all?

Answer:
Find the yards of red fabric by multiplying the yards of yellow fabric by 2.5
3.5×2.5=8.75(0.25+1.5+1+6)
8.75 yards of red fabric is required to make a dragon.
Add the yards of yellow and red fabric
3.5+8.75=12.25
Total fabric i need to buy to make a dragon is 12.25 yards.
Question 15.
An employee cleans the surface of the rectangular ice rink. What is the area of the ice rink?
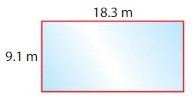
Answer:
Ice rink here is in rectangular shape.
Area of a rectangle is length × breadth
Length of ice rink is 18.3 m, breadth of ice rink is 9.1 m
18.3×9.1=0.03+2.7+1.8+162
Area of ice rink is 166.53 square meters
Question 16.
There are 89.1 milligrams of Vitamin C in 1 cup of strawberries. There are 83.2 milligrams of Vitamin C in 1 cup of orange slices. You eat2.5 cups of strawberries and 1.5 cups of orange slices. How much Vitamin C do you consume?
Answer:
Multiply vitamin C in 1 cup of strawberries with 2.5
89.1×2.5=222.75
Multiply vitamin C in 1 cup of orange slices with 1.5
83.2×1.5=124.8
Add both the quantities 222.75+124.8=347.55
Total vitamin c consumed by me is 347.55 milligrams.
Use Partial Products to Multiply Decimals Homework & Practice 5.6
Find the product. Check whether your answer is reasonable.
Question 1.

Answer:
2.4×1.2=
1.Multiply the tenths by tenths =0.4×0.2=0.08
2.Multiply the ones by tenths = 0.4×1=0.4
3.Multiply the tenths by ones = 2×0.2=0.4
4.Multiply the ones by ones =2×1=2
Add all the partial products =0.08+0.4+0.4+2=2.88
Therefore 2.4×1.2=2.88
Question 2.

Answer:
3.1×6.7
1.Multiply the tenths by tenths =0.1×0.7=0.07
2.Multiply the ones by tenths = 0.1×6=0.6
3.Multiply the tenths by ones = 3×0.7=2.1
4.Multiply the ones by ones =3×6=18
Add all the partial products =0.07+0.6+2.1+18=20.77
Therefore 3.1×6.7=20.77
Question 3.
Answer:
7.3×5.9=
1.Multiply the tenths by tenths =0.3×0.9=0.27
2.Multiply the ones by tenths = 0.3×5=1.5
3.Multiply the tenths by ones = 7×0.9=6.3
4.Multiply the ones by ones =7×5=35
Add all the partial products =0.27+1.5+6.3+35=42.07
Therefore 7.3×5.9=43.07
Find the product. Check whether your answer is reasonable.
Question 4.
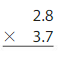
Answer:
2.8×3.7
1.Multiply the tenths by tenths =0.8×0.7=0.56
2.Multiply the ones by tenths = 0.8×3=2.4
3.Multiply the tenths by ones = 2×0.7=1.4
4.Multiply the ones by ones =2×3=6
Add all the partial products =0.56+2.4+1.4+6=10.36
Therefore 2.8×3.7=10.36
Question 5.
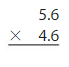
Answer:
5.6×4.6
1.Multiply the tenths by tenths =0.6×0.6=0.36
2.Multiply the ones by tenths =0.6×4=2.4
3.Multiply the tenths by ones =0.6×5=3
4.Multiply the ones by ones =5×4=20
Add all the partial products =0.36+2.4+3+20=25.76
Therefore 5.6×4.6=25.76
Question 6.
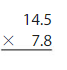
Answer:
14.5×7.8=
1.Multiply the tenths by tenths =0.5×0.8=0.4
2.Multiply the ones by tenths = 0.5×7=3.5
3.Multiply the tenths by ones = 14×0.8=11.2
4.Multiply the ones by ones =14×7=98
Add all the partial products =0.4+3.5+11.2+98=133.1
Therefore 14.5×7.8=113.1
Question 7.
21.4 × 9.3 = ______
Answer:
21.4×9.3=
1.Multiply the tenths by tenths =0.4×0.3=0.12
2.Multiply the ones by tenths = 0.4×9=3.6
3.Multiply the tenths by ones = 21×0.3=6.3
4.Multiply the ones by ones =21×9=189
Add all the partial products =0.12+3.6+6.3+189=199.02
Therefore 21.4×9.3=199.02
Question 8.
58.1 × 8.6 = ______
Answer:
58.1×8.6=
1.Multiply the tenths by tenths =0.1×0.6=0.06
2.Multiply the ones by tenths = 0.1×8=0.8
3.Multiply the tenths by ones = 58×0.6=34.8
4.Multiply the ones by ones =58×8=464
Add all the partial products =0.06+0.8+34.8+464=499.66
Therefore 58.1×8.6=499.66
Question 9.
0.6 × 1.45 = ______
Answer:
0.6×1.45=
1.Multiply the tenths by tenths =0.6×0.45=0.27
2.Multiply the ones by tenths = 0.6×1=0.6
3.Multiply the tenths by ones = 0×0.45=0
4.Multiply the ones by ones =0×1=0
Add all the partial products =0.27+0.6+0+0=0.87
Therefore 0.6×1.45=0.87
Question 10.
Writing
How is multiplying two decimals different than multiplying a whole number and a decimal?
Answer:
You have to line up the decimals in the two numbers with decimals, but the decimal and the whole numbers you don’t have to line up the decimals because there is only one number with a decimal.
Question 11.
DIG DEEPER!
Two numbers each have one decimal place. Is it possible for their product to be a whole number? Explain.
Answer:
No. When you multiply something by a decimal, you make it smaller. Since you’ve started with something smaller than a whole number, and then you make it smaller, the answer will always be less than a whole number, and thus never a whole number
Question 12.
Modeling Real Life
A red-bellied snake is 11.5 inches long. A ring-necked snake is 1.4 times as long as the red-bellied snake. How much longer is the ring-necked snake than the red-bellied snake?

Answer:
To find the length of a ring‐necked snake multiply the length of red‐bellied snake by 1.4
11.5×1.4=16.1
Length of ring‐necked snake is 16.1 inches.
Subtract 11.5 from 16.1=4.6 inches.
4.6 inches much longer is the ring-necked snake than the red-bellied snake.
Question 13.
Modeling Real Life
You use 2 cans of tomato sauce with mushrooms and 1.5 cans of plain tomato sauce to make lasagna. Each can contains 10.5 ounces. How many ounces of tomato sauce are in the lasagna?
Answer:
Each can contains 10.5 ounces of tomato sauce
2 cans contains 2×10.5=21 ounces
1.5 cans of plain sauce contains
1.5×10.5=15.75 ounces of sauce
Add 21 and 15.75 to find ounces of tomato sauce in the lasagna
21+15.75=36.75 ounces.
36.75 ounces of tomato sauce are in the lasagna.
Review & Refresh
Find the product.
Question 14.
24 × 104 = ______
Answer:
24×10000=240000
Question 15.
700 × 30 = ______
Answer:
700×30=21000
Question 16.
200 × 600 = _______
Answer:
200×600=120000
Lesson 5.7 Use Strategies to Multiply Decimals
Explore and Grow
Without multiplying, determine the pairs of expressions that have the same value. Explain your reasoning.

Answer:
Reasoning
How do you know how many decimal places are in each product? Explain.
Answer:
The number of decimal places in each product is the sum of decimal places in the multiplyer and the multiplicand.
Think and Grow: Use Strategies to Multiply
You can use estimation and place value, or multiplication properties to multiply.
Example
Find 3.84 × 2.1. Estimate _______
Multiply 384 by21. Then place the decimal point.
Because the product should be close to your estimate, place the decimal point after the ______.
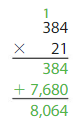
So, 3.84 × 2.1 = _____.
Example
Find 0.3 × 0.7.
You can use properties to multiply.

Show and Grow
Find the product. Explain the strategy you used.
Question 1.
4.91 × 0.8 = _____
Answer:
Estimate:4×1=4
Multiply 491×8=3928
Then place the decimal point.
Because the product should be close to your estimate, place the decimal point after one digit ie thousands place.
3.928
Question 2.
10.2 × 5.6 = ______
Answer
Estimate:10×6=60
Multiply 102×56=5712
Then place the decimal point.
Because the product should be close to your estimate, place the decimal point after one digit ie thousands place.
57.12
Question 3.
12.03 × 4.2 = ______
Answer:
Estimate:12×4=48
Multiply 1203×43=51729
Then place the decimal point.
Because the product should be close to your estimate, place the decimal point after two digits ie thousands place.
51.729
Apply and Grow: Practice
Find the product. Explain the strategy you used.
Question 4.
0.9 × 3.2 = _____
Answer:
Estimate:1×3=3
Multiply 9×32=288
Then place the decimal point.
Because the product should be close to your estimate, place the decimal point after one digit ie hundreds place.
2.88
Question 5.
1.7 × 0.84 = ______
Answer:
Estimate:2×1=2
Multiply 17×84=1428
Then place the decimal point.
Because the product should be close to your estimate, place the decimal point after one digit ie thousands place.
1.428
Question 6.
2.4 × 2.4 = ______
Answer:
Estimate:2×3=6
Multiply 24×24=576
Then place the decimal point.
Because the product should be close to your estimate, place the decimal point after one digit ie hundreds place.
5.76
Question 7.
12.1 × 0.8 = ______
Answer:
Estimate:12×1=12
Multiply 121×8=968
Then place the decimal point.
Because the product should be close to your estimate, place the decimal point after one digit ie hundreds place.
9.68
Question 8.
0.05 × 0.9 = ______
Answer:
Think: 0.05=5×0.01 and 0.9=9×0.1
Use properties to multiply (commutative property of multiplication and associative property of multiplication)
0.05×0.9=5×0.01×9×0.1
=(5×9)×(0.1×0.01)
=45(0.001)
=0.045
Multiplying 45 by 0.001 moves the decimal point three places to the left.
Therefore 0.05×0.9=0.045.
Question 9.
7.4 × 8.6 = ______
Answer:
Estimate:7×9=63
Multiply 74×86=6364
Then place the decimal point.
Because the product should be close to your estimate, place the decimal point after two digits ie hundreds place.
63.64
Question 10.
A newly hatched fish is 0.25 inch long. An adult fish is 7.6 times as long as the newly hatched fish. How long is the adult fish?

Answer:
A newly hatched fish is 0.25 inch long, An adult fish is 7.6 times as long as the newly hatched fish.
Multiply 7.6 by 0.25
7.6×0.25=(76×25)×(0.1×0.01)=1900×0.001=1.9Therefore the adult fish is 1.9 inches long.
Question 11.
Writing
Which strategy do you prefer to use to multiply decimals? Explain.
Answer:
I prefer estimate strategy as it is very easy find the product of decimals by estimating the product of their whole numbers and placing the decimal point.
Question 12.
Structure
Your friend multiplies two decimals by rewriting the product as (56 × 3) × (0.01 ×0.1). What two decimals could she be multiplying?
Answer:
My friend multiplies two decimals by rewriting the product as (56 × 3) × (0.01 ×0.1)
Use multiplication properties.
(56 × 3) × (0.01 ×0.1)=(56×0.01)×(3×0.1)=0.56×0.3
Therefore my friend multiplied 0.56 by 0.3.
Question 13.
Precision
How many decimal places are in the unknown factor? Explain
_____ × 2.8 = 4.48
Answer:
_____ × 2.8 = 4.48
In the above equation the multiplicand in the equation has one decimal place after decimal point.
As the product has two decimal places after the decimal point the multiplyer will also have 1 digit after decimal point.
Therefore there is one decimal place is in the unknown factor.
Think and Grow: Modeling Real Life
Example
You measure the distance between Los Angeles and Anaheim on a map. Each centimeter represents 2.5 kilometers. What is the actual distance between the cities?
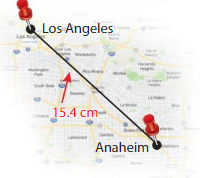
Because each centimeter represents 2.5 kilometers, multiply 15.4 and 2.5 to find the actual distance.
Multiply 154 by 25. Then place the decimal point. Estimate ______
Because the product should be close to your estimate, place the decimal point after the ______
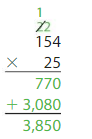
15.4 × 2.5 = _______
So, the actual distance between the cities is _________ kilometers.
Show and Grow
Question 14.
You measure the height of the replica of the Lincoln statue. Each centimeter represents 2.5 meters. What is the actual height of the Lincoln statue?

Answer:
Because each centimeter represents 2.5 meters, multiply 2.32 and 2.5 to find the actual height.
Multiply 232 by 25. Then place the decimal point. Estimate 232×25
Because the product should be close to your estimate, place the decimal point after the one digit ie 3 places from the left.
232×25=5800
2.32 × 2.5 = 5.800=5.8
So, the actual height is 5.8 meters
Therefore the actual height of the Lincoln statue is 5.8 meters.
Question 15.
DIG DEEPER!
How much does the bunch of bananas cost? Explain.

Answer:
The above picture tells us that there are 2.3 pounds of bananas.
Each pound of banana costs $0.59
To find the cost of 2.3 pounds of bananas
Multiply 2.3×0.59=
Estimate
Because the product should be close to your estimate, place the decimal point after the one digit ie 3 places from the left
23×59=1357
Therefore 2.3×0.59=1.357
Question 16.
DIG DEEPER!
Your friend has a digital photograph file that is 0.25 mega byte larger than 7.5 times the file size of your photograph. What is the file size of your friend’s photograph?
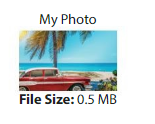
Answer:
File size of my photograph is 0.5 MB
My friend has a digital photograph file that is 0.25 mega byte larger than 7.5 times the file size of my photograph.
Estimate
Multiply 0.5×7.5
(5×75)×(0.1×0.1)=375×0.01=3.75 MB
Because the product should be close to your estimate, place the decimal point after the one digit ie 2 places from the left
Add 0.25 MB to 3.75 MB
=3.75+0.25=4 MB
The file size of my friend’s photograph is 4 MB.
Use Strategies to Multiply Decimals Homework & Practice 5.7
Find the product. Explain the strategy you used.
Question 1.
0.8 × 1.4 = ______
Answer:
Estimate:1×1=1
Multiply 8×14=112
Then place the decimal point.
Because the product should be close to your estimate, place the decimal point after one digit ie hundreds place.
1.12
Question 2.
1.3 × 2.9 = ______
Answer:
Estimate:1×3=3
Multiply 13×29=377
Then place the decimal point.
Because the product should be close to your estimate, place the decimal point after one digit ie hundreds place.
3.77
Question 3.
1.7 × 0.6 = ______
Answer:
Estimate:1×1=1
Multiply 17×6=102
Then place the decimal point.
Because the product should be close to your estimate, place the decimal point after one digit ie hundreds place.
1.02
Question 4.
3.86 × 2.8 = ______
Answer:
Estimate:3×3=9
Multiply 386×28=10808
Then place the decimal point.
Because the product should be close to your estimate, place the decimal point after two digits ie hundreds place.
10.808
Question 5.
0.07 × 4.5 = _______
Answer:
Estimate:0x4=0
Multiply 7×45=315
Then place the decimal point.
Because the product should be close to your estimate, place the decimal point before three digits ie hundreds
place.
0.315
Question 6.
2.56 × 6.25 = ______
Answer:
Estimate:3×6=18
Multiply 256×625=160000
Then place the decimal point.
Because the product should be close to your estimate, place the decimal point after two digits ie ten thousands place.
16.0000=16
Question 7.
1.18 × 0.8 = ______
Answer:
Estimate:1×1=1
Multiply 118×8=944
Then place the decimal point.
Because the product should be close to your estimate, place the decimal point before three digits ie hundreds place.
0.944
Question 8.
18.2 × 0.9 = ______
Answer:
Estimate:18×1=18
Multiply 182×9=1638
Then place the decimal point.
Because the product should be close to your estimate, place the decimal point after two digits ie hundreds place.
16.38
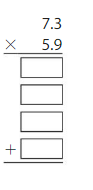
Question 9.
6.7 × 5.2 = ______
Answer:
Estimate:7×5=35
Multiply 67×52=3484
Then place the decimal point.
Because the product should be close to your estimate, place the decimal point after two digits ie hundreds place.
34.84
Question 10.
A beaker contains 0.75 liter of a solution. You use 0.1 of the solution for an experiment. How much of the solution do you use?

Answer:
To find the amount of solution used multiply 0.75 by 0.1
0.75×0.1=0.075
0.075 litrrs of solution is used.
Question 11.
Structure
Which expressions are equivalent to 0.6 × 0.3?
(6 × 3) × (0.1 × 0.1)
(6 × 3) × (0.01 × 0.01)
(6 × 3) × (\(\frac{1}{10}\) × \(\frac{1}{10}\))
(6 × 0.1) × (3× 0.1)
Answer:
(6 × 3) × (0.1 × 0.1), (6 × 0.1) × (3× 0.1) are equivalent to 0.6×0.3 as their product is equal to the product of 0.6×0.3.
Question 12.
Number Sense
Your friend finds 0.92 × 0.3 by multiplying 92 and 3. Explain how your friend will know where to place the decimal point in the product.
Answer:
My friend finds 0.92×0.3 by multiplying 92 and 3
In 0.92 there are two digits after decimal point and in 0.3 there are three digits after decimal point so the product should have 3 digits after decimal point.
When we multiply 92 by 3 the product is 276
Therefore the decimal point is placed before 3 digits from the left 0.276 will be the product.
Question 13.
Number Sense
When finding 75 × 0.01, where will the decimal point be placed? Explain.
Answer:
While finding the product of 75 and 0.01 the decimal point will be placed before two digits as the decimal point in 0.01 has two places after decimal.
Therefore 0.75 is the product and decimal point is placed two places from the left.
Question 14.
Modeling Real Life
A toy car designer measures the length of the actual car shown. A toy car is 0.05 times as long as the actual car. How long is the toy car?

Answer:
A toy car designer measures the length of the actual car shown.
Length of the actual car is 160.6 inches
A toy car is 0.05 times as long as the actual car
Multiply 160.6×0.05=8.03
Therefore Toy car is 8.03 inches long.
Question 15.
Modeling Real Life
A carpet installer measures 3 rectangular bedrooms for new carpeting. Which bedroom needs the most carpeting?
Bedroom A: 3.1 meters by3.1 meters
Bedroom B: 2.9 meters by3.2 meters
Bedroom C: 2.5 meters by3.4 meters160.6 inches
Answer:
Bedroom A: 3.1×3.1= (31×31)×(0.1×0.1)=961×0.01=9.61
Bedroom B: 2.9×3.2=(29×32)×(0.1×0.1)=928×0.01=9.28
Bedroom C: 2.5×3.4=(25×34)×(0.1×0.1)=850×0.01=8.50
Bedroom A needs the most carpeting.
Review & Refresh
Question 16.
Round 4.163
Nearest whole number: ______
Nearest tenth: ______
Nearest hundredth: ______
Answer:
Nearest whole number: 4
Nearest tenth: 4.2
Nearest hundredth: 4.16
Question 17.
Round 10.187.
Nearest whole number: ______
Nearest tenth: ______
Nearest hundredth: ______
Answer:
Nearest whole number:10
Nearest tenth: 10.2
Nearest hundredth: 10.19
Lesson 5.8 Multiply Decimals
Explore and Grow
Choose any strategy to find each product.

Answer:
0.8×0.4=
Estimate
=(8×4)×(0.1×0.1)
=32(0.01)
= 0.32
0.8×0.4=0.32
2.1×1.25=
Use partial products
2.1×1.25=
0 .1×0.25=0.025
0 .1×1=0.1
0 .25×2=0.5
2×1=2
2.1×1.25=0.025+0.1+0.5+2=2.625
0.22×4.5
Estimate and place value
22×45=990
There are 3 decimal places in the factors so place the decimal point before three digits ie hundreds place.
0.990=0.99
0.22×4.5=0.99
1.4×1.6
Think: 1.4=14×0.1 and 1.6=16×0.1
Use properties to multiply (commutative property of multiplication and associative property of multiplication
=1.4×1.6
=14×0.1×16×0.1
=(14×16)×(0.1×0.1)
=224(0.01)
= 2.24
Reasoning
How can you determine the number of decimal places a product will have before multiplying?
Answer:
The decimal places of the product is the sum of the decimal places of the factors.
Think and Grow: Multiply Decimals
Key Idea
To multiply decimals, multiply as you do with whole numbers. The number of decimal places in the product is equal to the sum of the number of decimal places in the factors.
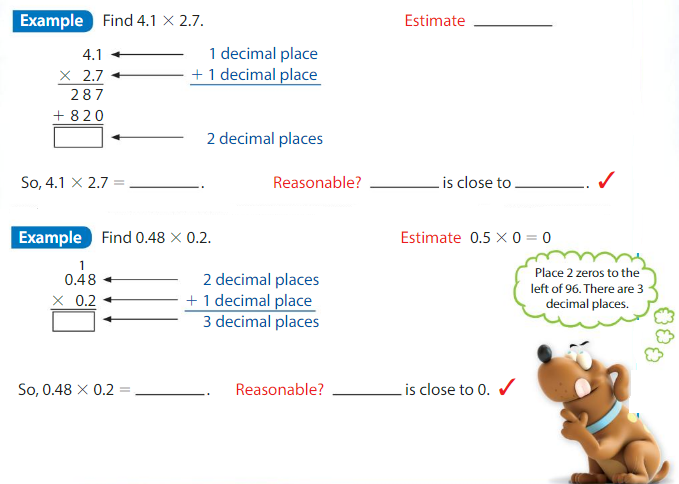
Show and Grow
Find the product.
Question 1.
Answer:
1.8×7.3
Multiply the whole numbers first and place the decimal points
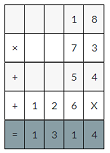
18×73=1314
There are 1 decimal place each in both the factors so the product will have 2 decimal places
Place the decimal point before 2 digits feom the left 13.14
Therefore 1.8×7.3=13.14
Question 2.
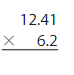
Answer:
12.41×62
Multiply the whole numbers first and place the decimal points
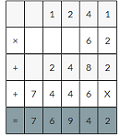
1241×62=76942
There are 2 decimal places and 1 decimal each in both the factors so the product will have 3 decimal
places
Place the decimal point before three digits from the left 76.942
Therefore 12.41×62=76.942
Question 3.
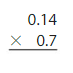
Answer:
0.14×0.7
Multiply the whole numbers first and place the decimal points
14×7=98
There are 2 decimal places and 1 decimal place each in both the factors so the product will have 3 decimal
places
Place the decimal point before three digits from the left 0.098
Therefore 0.14×0.7=0.098
Apply and Grow: Practice
Find the product.
Question 4.
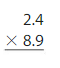
Answer:
2.4×8.9
Multiply the whole numbers first and place the decimal points
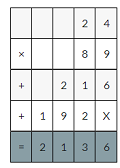
24×89=2136
There are 1 decimal places each in both the factors so the product will have 2 decimal places
Place the decimal point before two digits from the left 21.36
Therefore 2.4×8.9=21.36
Question 5.
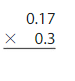
Answer:
0.17×0.3
Multiply the whole numbers first and place the decimal points
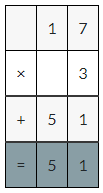
17×3=51
There are 2 decimal places and 1 decimal each in both the factors so the product will have 3 decimal
places
Place the decimal point before three digits from the left 0.051
Therefore 0.17×0.3=0.051
Question 6.
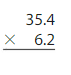
Answer:
35.4×6.2
Multiply the whole numbers first and place the decimal points
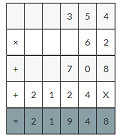
354×62=21948
There are 1 decimal place each in both the factors so the product will have 2 decimal places
Place the decimal point before two digits from the left 219.48
Therefore 35.4×62=219.48
Question 7.
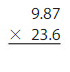
Answer:
9.87×23.6
Multiply the whole numbers first and place the decimal points
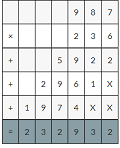
987×236=232932
There are 2 decimal places and 1 decimal each in both the factors so the product will have 3 decimal
places
Place the decimal point before three digits from the left 232.932
Therefore 9.87×23.6=232.932
Question 8.
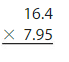
Answer:
16.4×7.95
Multiply the whole numbers first and place the decimal points
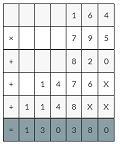
164×795=130380
There are 2 decimal places and 1 decimal each in both the factors so the product will have 3 decimal
places
Place the decimal point before three digits from the left 130.380
Therefore 16.4×79.5=130.380
Question 9.
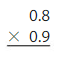
Answer:
0.8×0.9
Multiply the whole numbers first and place the decimal points
8×9=72
There are 1 decimal place each in both the factors so the product will have 2 decimal places
Place the decimal point before two digits from the left 0.72
Therefore 0.8×0.9=0.72
Question 10.
46.5 × 0.73 = ______
Answer:
46.5×0.73
Multiply the whole numbers first and place the decimal point
465×73=33945
There are 2 decimal places and 1 decimal each in both the factors so the product will have 3 decimal
places
Place the decimal point before three digits from the left 33.945
Therefore 46.5×0.73=33.945
Question 11.
14.8 × 9.3 = ________
Answer:
14.8×9.3
Multiply the whole numbers first and place the decimal points
148×93=13764
There are 1 decimal place each in both the factors so the product will have 2 decimal places
Place the decimal point before two digits from the left 137.64
Therefore 14.8×9.3×=137.64
Question 12.
1.54 × 2.6 = ______
Answer:
1.54×2.6
Multiply the whole numbers first and place the decimal points
154×26=4004
There are 2 decimal places and 1 decimal each in both the factors so the product will have 3 decimal
places
Place the decimal point before three digits from the left4.004
Therefore 1.54×2.6=4.004
Question 13.
A sugar glider weighs 0.35 times the weight of the pygmy slow loris. How much does the sugar glider weigh?

Answer:
A sugar glider weighs 0.35 times the weight of the pygmy slow loris
Weight of pygmy slow loris is 14.9 ounces
Multiply 14.9 by 0.35 to find the weight of sugar glider 14.9×0.35=
149×35
5215
There are 3 decimal places in the factors so the product will have 3 decimal places
Place the decimal point before 3 digits from the left. 5.215
Therefore 14.9×0.35=5.215
Question 14.
Structure
Use the equation to write two different multiplication expressions that have products of 28.34.
109 × 26 = 2,834
Answer:
Equation 1:10.9×2.6=28.34
Equation 2:109×26×0.1×0.1=28.34
Question 15.
DIG DEEPER!
Without calculating, explain how many decimal places are in the product 0.6 0.4 1.9. Rewrite the expression as the product of two decimals to support your answer.
Answer:
0.6 × 0.4 × 1.9
= 0.456
Think and Grow: Modeling Real Life
Example
Nutritionists recommend that fifth-graders should consume about 28 grams of fiber each day. One serving of broccoli contains 3.8 grams of fiber. You eat 4.5 servings of broccoli in 1 day. Do you consume enough fiber for the day by eating broccoli? Explain.

Multiply 3.8 by4.5 to find how many grams of fiber you consume by eating broccoli.
Compare the product to 28.
So, you ______ consume enough fiber for the day by eating broccoli.
Show and Grow
Question 16.
Your aunt drives a car from Cincinnati to Nashville. The car travels 30.4 miles using 1 gallon of gasoline. There are 6.5 gallons of gasoline in the tank. Can she drive the entire distance without adding more gas to the 6.5 gallons already in the tank? Explain.
Answer:
My aunt drives a car from Cincinnati to Nashville.
The distance from cincinnati to Nashville is 274 miles
The car travels 30.4 miles using 1 gallon of gasoline, There are 6.5 gallons of gasoline in the tank.
To find the total distance that my aunt can travel by using 6.5 gallons of gasoline
Multiply 6.5×30.4=65×304
65×304=19760
Place the decimal point before 2 digits from the left 197.60 miles
197.6<274 miles
So, my aunt cannot drive the entire distance without adding more gas to the 6.5 gallons already in the tank.
Question 17.
DIG DEEPER!
The equation shows how to convert a temperature C in degrees Celsius to a temperature F in degrees Fahrenheit. Convert the temperature shown to Fahrenheit.
1.8 × C + 32 = F

Answer:
Given 1.8×C+32=F
In the above picture the temperature is 37.1°C
To find degrees in Farenheit
Multiply 1.8 by 37.1 and add 32 to the product.
1.8×37.1=66.78+32=98.78°F
Therefore the temperature is 98.78°Farenheit.
Question 18.
DIG DEEPER!
Pennies dated 1982 or later contain about 0.06 gram of copper. Pennies dated prior to 1982 contain about 49.2 times as much copper as newer pennies. How many total grams of copper are in the pennies shown?

Answer:
Pennies dated 1982 or later contain about 0.06 gram of copper
There is 3 pennies which are dated after 1983
Multiply 3×0.06=0.18
Pennies dated prior to 1982 contain about 49.2 times as much copper as newer pennies
Multiply 49.2 by the copper in penny dated after 1982 ie 0.06
49.2×0.06=2.952
Multiply 49 by 6 and place the decimal point before 3 digits from the left
Add 0.18 to 2.952 to find the total amount of copper in all the coins
2.952+0.18=3.132 grams
The total amount of copper in all the coins is 3.132 grams.
Multiply Decimals Homework & Practice 5.8
Find the product.
Question 1.
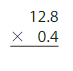
Answer:
12.8×0.4
Multiply the whole numbers first and place the decimal points
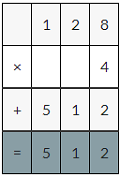
128×4=512
There are 1 decimal place each in both the factors so the product will have 2 decimal places
Place the decimal point before two digits from the left 5.12
Therefore 12.8×0.4=512
Question 2.
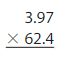
Answer:
3.97×62.4
Multiply the whole numbers first and place the decimal point
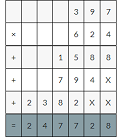
397×624=247728
There are 2 decimal places and 1 decimal each in both the factors so the product will have 3 decimal
places
Place the decimal point before three digits from the left 247.728
Therefore 3.97×62.4=247.728
Question 3.
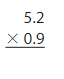
Answer:
5.2×0.9
Multiply the whole numbers first and place the decimal points
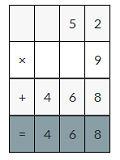
52×9=468
There are 1 decimal place each in both the factors so the product will have 2 decimal places
Place the decimal point before two digits from the left 4.68
Therefore 5.2×0.9=4.68
Question 4.
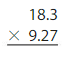
Answer:
18.3×9.27
Multiply the whole numbers first and place the decimal point
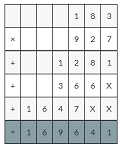
183×927=169641
There are 2 decimal places and 1 decimal each in both the factors so the product will have 3 decimal places
Place the decimal point before three digits from the left 169.641
Therefore 18.3×9.27=169.641
Question 5.
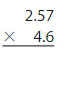
Answer:
2.57×4.6
Multiply the whole numbers first and place the decimal point
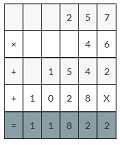
257×46=11822
There are 2 decimal places and 1 decimal each in both the factors so the product will have 3 decimal places
Place the decimal point before three digits from the left 11.822
Therefore 2.57×4.6=11.822
Question 6.
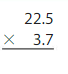
Answer:
22.5×3.7
Multiply the whole numbers first and place the decimal point
225×37=8325
There are 1 decimal place each in both the factors so the product will have 2 decimal places
Place the decimal point before 2 digits from the left 83.25
Therefore 22.5×3.7=83.25
Question 7.
0.89 × 0.3 = ______
Answer:
0.89×0.3
Multiply the whole numbers first and place the decimal point
89×3=267
There are 2 decimal places and 1 decimal each in both the factors so the product will have 3 decimal
places
Place the decimal point before three digits from the left 0.269
Therefore 0.89×0.3=0.269
Question 8.
7.1 × 5.6 = ______
Answer:
7.1×5.6
Multiply the whole numbers first and place the decimal points
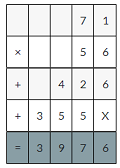
71×56=3976
There are 1 decimal place each in both the factors so the product will have 2 decimal places
Place the decimal point before two digits from the left 39.76
Therefore 7.1×5.6=39.76
Question 9.
13.63 × 9.2 = ______
Answer:
13.63×9.2
Multiply the whole numbers first and place the decimal point
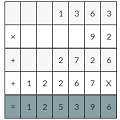
1363×92=125396
There are 2 decimal places and 1 decimal each in both the factors so the product will have 3 decimal
places
Place the decimal point before three digits from the left 125.396
Therefore 13.63×9.2=125.396
Question 10.
The Miniature pinscher weighs 0.12 times the weight of the Doberman pinscher. How much does the Miniature pinscher weigh?

Answer:
The Miniature pinscher weighs 0.12 times the weight of the Doberman pinscher
Weight of Doberman pinscher is 32.65 kilograms
Multiply 3265 by 12 and place the decimal point before 4 digits from the left.
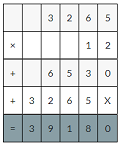
Weight of miniature pinscher is 32.65×0.12=3.918
Miniature pinscher weigh is 3.918 kilograms.
Question 11.
Reasoning
Explain how you can tell which product is greater without multiplying or estimating.
3.75 × 922 or 37.5 × 9.22
Answer:
Product of 3.75 × 922 is greater because the number contains bigger whole number when compared to the other product.
Question 12.
Modeling Real Life
Nutritionists recommend that fifth-graders should consume about 5 ounces of protein each day. One serving of yogurt contains 0.6 ounce of protein. You eat 2.5 servings of yogurt in 1 day. Do you consume enough protein for the day by eating yogurt? Explain.

Answer:
Nutritionists recommend that fifth-graders should consume about 5 ounces of protein each day.
One serving of yogurt contains 0.6 ounce of protein.
If i eat 2.5 servings of yogurt in 1 day then i consume 2.5×0.6 ounce sof protein per day
Multiply 25 by 6 and place the decimal point 2before 2 digitd from the left
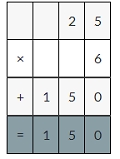
2.5×0.6=1.5 ounces of protein
Compare 1.5 with 5
1.5<5
So, i cannot consume enough protein for the day by eating yogurt.
Question 13.
DIG DEEPER!
Each 18-karat gold ring shown is a mixture of gold and other metals. One gram of 18-karat gold contains 0.75 gram of gold. How many total grams of gold are in the rings shown?

Answer:
Each 18-karat gold ring shown is a mixture of gold and other metals.
If one gram of 18-karat gold contains 0.75 gram of gold then
Multiply 18 by 75 and place the decimal point before 3 digits from the left
1.8 grams ring contains 1.8×0.75 grams of gold 1.8×0.75=1.35 grams of gold.
Multiply 19 by 75 and place the decimal point before 3 digits from the left
1.9 grams ring contains 1.9×0.75 grams of gold 1.9×0.75=1.425 grams of gold
Multiply 21 by 75 and place the decimal point before 3 digits from the left
2.1 grams ring contains 2.1×0.75 grams of gold 2.1×0.75=1.575 grams of gold
Add 1.35 , 1.425 and 1.575 to find the total grams of gold 1.35+1.425+1.575=4.35
Total 4.35 grams of gold are in the rings shown.
Review & Refresh
Write the words as an expression. Then interpret the expression.
Question 14.
Subtract 10 from 50, then divide by 5
Answer:
8
Explanation:
Subtract 10 from 50=50‐10=40
divide by 5=40÷5=8
Question 15.
Add the product of 12 and 6 to the product of 6 and 8.
Answer:
120
Explanation:
product of 12 and 6=12×6=72
product of 6 and 8=6×8=48
Add the product of 12 and 6 to the product of 6 and 8=72+48=120
Lesson 5.9 Problem Solving: Multiply with Money
Explore and Grow
Explain how you would estimate the cost of 1.9 pounds of ham, 0.8 pound of turkey, and 1 pound of cheese.

Answer:
At Descartes’s Deli the Ham costs $8.90;per pound , Turkey costs $9.80 per pound and Cheese costs $6.70 per pound
Estimated solution
Use rounding
Cost of ham is 9, cost of turkey is 10 and cost of cheese is 7 per pound
By using rounding to find
Cost of 2 pounds of ham=2×9=18
Cost of 1 pound of turkey=10
Cost of 1 pound of cheese=7
Total =18+10+7=35
Original solution
To find the cost of
1.9 pounds of ham, Multiply 1.9×$8.9=$16.91
0.8 pound of turkey, Multiply 0.8×$9.8=$7.84
1 pound of cheese , Multiply 1×$6.7=$6.7
Therefore Total cost is $16.91+$7.84+$6.7=$31.45.
Reasoning
Is your answer an overestimate or an underestimate? Explain.
Answer:
My answer is an overestimate as it is more than the actual cost.
Think and Grow: Problem Solving: Multiply with Money
Example
Carrots cost $0.90 per pound. You buy 2.6 pounds of carrots and give the cashier $5. How much change do you receive?

Understand the Problem
What do you know?
• Carrots cost $0.90 per pound.
• You buy 2.6 pounds of carrots.
• You pay with $5.
What do you need to find?
• You need to find the amount of change you receive.
Make a Plan
How will you solve?
Write and solve an equation: Multiply the number of pounds by the cost per pound, and subtract from $5.
Solve
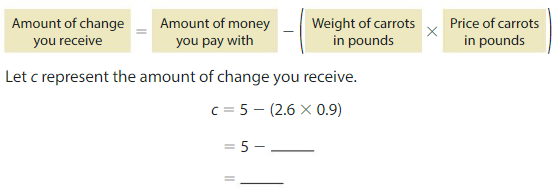
So, you receive $ ______ in change.
Show and Grow
Question 1.
Landscaping rocks cost $0.35 per pound. A landscaper buys 86.4 pounds of rocks with $40. How much change does she receive?
Answer:
What i know is
Cost of landscaping rocks per pound is $0.35
A landscaper buys 86.4 pounds of rocks with $40
What i need to find is the change landscaper receives.
The amount of change landscaper receives =Amount spent ‐cost of rock per pound × 86.4 pounds of rock
=($40)‐($0.35×86.4)=$40‐$30.24=$9.76
$9.76 is the change landscaper receives.
Apply and Grow: Practice
Understand the problem. What do you know? What do you need to find? Explain.
Question 2.
A gallon of milk cost $0.82 in 1960. In2015, it cost $0.03 more than 4 times the cost in 1960. How much did a gallon of milk cost in 2015?

Answer:
What we know is
The cost of gallon of milk in 1960 is $0.82
What we have find is
The Cost of gallon of milk in 2015 is
(4×$0.82)+$0.03=$3.28+$0.03=$3.31
A gallon of milk cost in 2015 is $3.31
Question 3.
A secretary earns $10.75 each hour. He works 8 hours each day,5 days each week. How much money does he earn in 1 week?
Answer:
What we know is
A secretary earns $10.75 each hour, he works 8 hours each day,5 days each week
What we have to find is
The amount he earns in a weekIf he works 8 hours each day and 5 days a week then he works for 40 hours in a week
The amount he earns in a week =Amount he earns per hour × Number of hours he work in a week.
=$10.75×40=$430
The money he earn in 1 week is $430.
Understand the problem. Then make a plan. How will you solve? Explain.
Question 4.
You download 8 songs for $1.29 each and 1 song for $0.99. How much do you pay for all of the songs?
Answer:
If i download 8 songs for $1.29 each then the money for 8 songs is number of songs multiplied by charges per
song
Ie 8×$1.29=$10.32
If i download another song for $0.99 then total charges i spent is charges of 8 songs plus charges of 1 song
$10.32+$0.99=$11.31
Therefore i pay $11.31 for all the songs.
Question 5.
Your friend buys a snack for $2.75, and a book that costs 5 times as much as the snack. He also buys a poster that costs $3.50 less than the book. How much does the poster cost?
Answer:
Cost of snack is $2.75
Book costs 5 times as much as the snack
The cost of book = 5×cost of snack
=5×$2.75=13.75
poster costs $3.50 less than the book
The cost of the poster = cost of book‐$3.50
=$13.75‐3.50=$10.25
Therefore cost of the poster is $10.25
Question 6.
A pair of shoes costs $35. Newton has a coupon topay 0.8 of the price.Descartes has a $10 off coupon. Who will pay more for the shoes?
Answer:
A pair of shoes costs $35
Newton has a coupon topay 0.8 of the price
=0.8×$35=28
Newton pays $28
Descartes has a $10 off coupon
=$35‐$10=$25
Descartes pay $25
28>25 so, Newton pays more for the pair of shoes.
Question 7.
Two friends eat at a restaurant for $34. They calculate the tip by multiplying $34 by 0.18. How much do they pay for the meal, including the tip?

Answer:
Two friends eat at a restaurant for $34
If they calculate the tip by multiplying $34 by 0.18
Amount of tip =0.18×$34=$6.12
The money they pay for the meal, including the tip =$34+$6.12=$40.12
Therefore the money they paid is $40.12.
Think and Grow: Modeling Real Life
Example
A traveler gives a cashier 100 U.S. dollars to exchange for European euros. A $7.50 service fee is deducted from the amount given. How many European euros does the traveler receive?
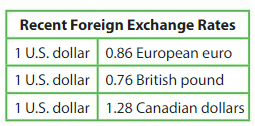
Think: What do you know? What do you need to find? How will you solve?

Answer:
m = (100 – 7.5) × 0.86
92.5 × 0.86
= 79.55
Show and Grow
Use the table above.
Question 8.
DIG DEEPER!
You need 50 Canadian dollars. You give a cashier 50 U.S. dollars to exchange for Canadian dollars. A $9.50 service fee is deducted from the amount given. Do you have enough Canadian dollars? Explain.
Answer:
I need 50 canadian dollars
I gave 50 U.S. dollars for exchange and the service fee is $9.50
Exchange rate for US dollar to canadian dollar is 1.28
So, 50 US dollars ×1.28=64 canadian dollars
64>50
Therefore i have enough Canadian dollars.
Question 9.
DIG DEEPER!
In the example, the traveler decides to exchange the same number of U.S. dollars for British pounds. Without calculating, determine whether the traveler receives more European euros or British pounds. Explain.
Answer:
The traveler receives more European euros because the exchange rate of European euros ia more than the
exchange rate of British pounds.
Problem Solving: Multiply with Money Homework & Practice 5.9
Understand the problem. Then make a plan. How will you solve? Explain.
Question 1.
One gallon of gasoline costs $2.75. Your cousin fills his car with 10 gallons of gasoline each week. How much money does he spend on gasoline in 1 year?
Answer:
One gallon of gasoline costs $2.75
My friend fills his car with 10 gallons of gasoline each week
We have to find the money he spend on gasoline for a year.
An year consists of 52 weeks
So, multiply 52 by 10 to find number of gallons used in a year
52×10=520
If Cost of a gallon of gasoline is $2.75 then cost of 52p gallons is $2.75×520=$1430
$1430 is the money spend by my cousin on gasoline in 1 year.
Question 2.
Newton buys a guitar for $46 and a guitar amplifier. The amplifier costs $1.54 more than 1.26 times the cost of the guitar. How much does the amplifier cost?
Answer:
Cost of guitar is $46
The amplifier costs $1.54 more than 1.26 times the cost of the guitar
Cost of amplifier = ($46×1.26)+$1.54
=$57.96+$1.54
$59.5
Therefore the amplifier costs $59.5.
Question 3.
One pound of cheese costs $3.98. You buy a box of crackers for $3.37 and 2.5 pounds of cheese. How much do you spend in all?
Answer:
One pound of cheese costs $3.98
Cost of 2.5 pounds of cheese =2.25×$3.98=$8.955
If i buy a box of crackers for $3.37 and 2.5 pounds of cheese
The money is spent =$3.37+$8.955=$12.325
$12.325 is the money i spend in all.
Question 4.
Writing
Write and solve a two-step word problem involving money.
Answer:
A boy buys a toy car for $3 and also a toy bike for 2.4 times as much as the cost of the toy car. Find the money spend by the boy in all.
Solution:
The cost of toy car is $3
Cost of toy bike is 2.4 × cost of toy car
=2.4×$3=$7.2
Add cost of toy car and toy bike =$3+$7.2=$10.2
The money spent by the boy in all is $10.2
Question 5.Modeling Real Life
You buy 2.75 pounds of pistachios and 2 pounds of cashews. Do you pay more for the pistachios or for the cashews? How much more?
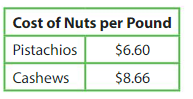
Answer:
Cost of pistachios per pound is $6.60
If i buy 2.75 pounds of pistachios then the money spend is 2.75×$6.60=$18.15
Cost of cashews per pound is $8.66
If i buy 2 pounds of cashews then the money spend is 2×$8.66=$17.32
18.15>17.32
So, i pay more for the pistachios.
Question 6.
Modeling Real Life
You, Newton, and Descartes sell items at a craft show. You earn $34.50. Newton earns 5 times as much as you do. Descartes earns 0.1 times as much as Newton does. How much do the three of you earn in all?
Answer:
You, Newton, and Descartes sell items at a craft show
Money i earned is $34.50
Newton earns 5 times as much as i do
Money earned by Newton is 5×$34.50=$172.5
Descartes earns 0.1 times as much as Newton does
Money earned by descartes is 0.1×$172.5=$17.25
Sum of $34.5, $172.5 and $17.25 is 224.25.
$22425 is the money the three earn in all.
Question 7.
DIG DEEPER!
A daycare employee earns $10.90 per hour for the first works in 1 week. He is paid 1.5 times that rate for each additional hour that he works. How much money does he earn working for 43 hours in 1 week?
Answer:
Given,
A daycare employee earns $10.90 per hour for the first works in 1 week.
He is paid 1.5 times that rate for each additional hour that he works.
10.90 × 1.5 = 16.35
16.35 × 43 = 703.05
Review & Refresh
Find the sum. Check whether your answer is reasonable.
Question 8.
24.93 + 3.86 = ______
Answer:
24.93 + 3.86 = 28.79
Explanation:
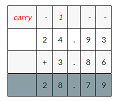
Question 9.
105.6 + 37.1 = _____
Answer:
105.6 + 37.1 = 142.7
Explanation:
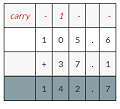
Multiply Decimals Performance Task
You study the different parts of a corn plant in science class.
Question 1.
You have a corn root sample and a corn stem sample on microscope slides. When you view the samples through a microscope, the magnification number tells you how many times larger the image will be than the actual size.You see only a portion of the enlarged image.
a. The corn root sample is 0.6 millimeter wide. You magnify the image by400. What is the width of the magnifiedCorn root corn root image?
b. You magnify the corn root sample by1,200. How much wider is the image when magnified by 1,200 than by 400?
c. You have a sample of a corn stem. The corn stem sample is 9.6 times wider than the corn root sample. What is the width of the corn stem sample?
Answer:
a.The corn root sample is 0.6 millimeter wide
If i magnify the image by 400 then the magnifird width =0.6×400=240 millimeters.
b.The corn root sample is 0.6 millimeter wide
If i magnify the image by 1200 then the magnifird width =0.6×1200=720 millimeters
Subtract 240 millimeters from 720 millimeters
480 millimeters wider is the image when magnified by 1,200 than by 400.
c.Given that the corn stem sample is 9.6 times wider than the corn root sample
The corn root sample is 0.6 millimeter wide
Width of corn stem =9.6 × width of corn root
=9.6×0.6=5.76 millimeters.
Question 3.
An ear of corn has about 16 rows of kernels. Each row has about 50 kernels of corn.
a. About 0.2 of the kernels are white and the rest are yellow. How many kernels are yellow?

b. Each ear of corn has about 0.25 pound of corn kernels. How many pounds of kernels are in a dozen ears of corn?
Answer:
a.An ear of corn contains 16×50=800kernels of corn
0.2 of corn are white 0.2×800=160
Subtract 160 from total number of kernels of corn =800‐160=640
Therefore number of yellow kernels of corn are 640.
b.Each ear of corn has about 0.25 pound of corn kernels.
Dozen corn ears contains 12×0.25 =3 pounds of corn kernels
3 pounds of kernels are in a dozen ears of corn.
Question 3.
You measure the growth of a corn stalk. The corn stalk grows about 1.75 inches each day.About how many inches does the plant growin 1 month? Justify your answer.
Answer:
The corn stalk grows about 1.75 inches each day.
If there are 30 days in a month then the length of corn stalk after month is 1.75 inches ×30=52.5 inches
Therefore, the plant grow 52.5 inches in 1 month.
Multiply Decimals Activity
Race Around the world: Multiplication
Directions:
1. Players take turns.
2. On your turn, flip a RaceAround the World: Multiplication Card and find the product.
3. Move your piece to the next number on the board that is highlighted in the product.
4. The first player to make it back to North America wins!

Multiply Decimals Chapter Practice
5.1 Multiplication Patterns with Decimals
Find the product.
Question 1.
0.9 ×103 = ______
Answer:
0.9×103 =900
Explanation:
0.9×1=0.9
0.9×10=9
0.9×100=90
0.9×1000=900
So, 0.9×103 =900
When we multiply 0.9 by 1000 the number of places of decimal point moves to the right is same as the exponent ie 3.
Question 2.
612.5 × 0.1 2 = ______
Answer:
612.5 × 0.1 2 =73.5
Multiply 6125 by 12 and place the decimal places before three places from the left.
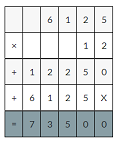
So, 612.5×0.12=73.5
Question 3.
30.1 × 102 = _____
Answer:
30.1×100=3010
Explanation:
30.1×1=30.1
30.1×10=301
30.1×100=3010
When we multiply 30.1 by 100 the number of places of decimal point moves to the right is same as the exponent ie 2.
So, 30.1×100=3010.
Question 4.
45.7 × 0.01 = ______
Answer:
45.7×0.01=0.457
Explanation:
45.7×1=45.7
45.7×0.1=4.57
45.7×0.01=0.457
When we multiply 45.7 by 0.01 the decimal point moves two places to the left
So, 45.7×0.01=0.457
Question 5.
8.6 × 10 = ______
Answer:
8.6×10=86
Explanation:
8.6×1=8.6
8.6×10=86
When we multiply 8.6 by 10 the decimal point moves 1 place to the right.
So, 8.6×10=86
Question 6.
5.24 × 0.1 = _______
Answer:
5.24×0.1=0.524
Explanation:
5.24×1=5.24
5.24×0.1=0.524
When we multiply 5.24 by 0.1 the decimal point moves one places to the left
So, 5.24×0.1=0.524
5.2 Estimate Products of Decimals and Whole Numbers
Estimate the product.
Question 7
0.99 × 45
Answer:
Use Rounding
1×45=45
0.99×45 is about 45
Question 8.
3.15 × 8
Answer:
Use Rounding
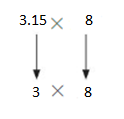
3×8=24
3.15×8 is about 24
Question 9.
17 × 1.68
Answer:
Use Rounding
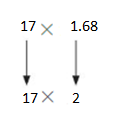
17×2=34
17×1.68 is about 34
Question 10.
95 × 5.02
Answer:
Use Rounding
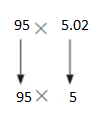
95×5=475
95×5.02 is about 475
5.3 Use Models to Multiply Decimals and Whole Numbers
Find the product.
Question 11.
0.3 × 3 = _____

Answer:
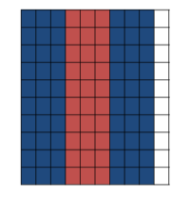
0.3+0.3+0.3 =0.9
Therefore 0.3×3=0.9
Question 12..
0.17 × 8 = _____

Answer:
0.17+0.17+0.17+0.17+0.17+0.17+0.17+0.17=1.36
Question 13.
Structure
Write an equation represented by the model.

Answer:
0.29×8=2.32
5.4 Multiply Decimals and Whole Numbers
Find the product.
Question 14.
3 × 1.64 = ______
Answer:
3×1.64=3×164
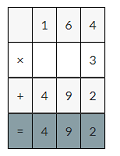
=492
Place the decimal point before 2 places from the left
4.92
Therefore 3 × 1.64 =4.92
Question 15.
2.3 × 8 = ______
Answer:
2.3×8=23×8
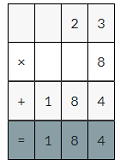
=184
Place the decimal point before 1 place from the left
18.4
Therefore 2.3×8=18.4
Question 16.
9 × 10.7 = ______
Answer:
9×10.7=9×107
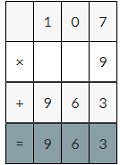
=963
Place the decimal point before 1 place from the left
96.3
Therefore 9×10.7=96.3
Question 17.
18.65 × 6 = _____
Answer:
18.65×6=1865×6
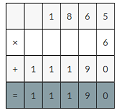
=11190
Place the decimal point before 2 places from the left
111.90
Therefore 18.65×6=111.90
5.5 Use Models to Multiply Decimals
Use the Models to find the product.
Question 18.
0.5 × 0.6 = ______

Answer:
Shade 5 rows to represent 0.5 and 6 column to represent 0.6
30 squares are shaded twice
So, 0.5×0.6=0.30
Question 19.
1.8 × 0.9 = _____
Answer:
Shade 9 rows to represent 0.9 and 18 columns to represent 1.8
162 squares are shaded twice
So, 1.8 × 0.9= 1.62
5.6 Use Partial Products to Multiply Decimals
Find the product. Check whether your answer is reasonable.
Question 20.
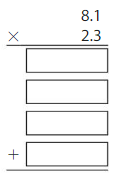
Answer:
Step 1:0.1×0.3=0.03
Step 2:0.1×2=0.2
Step 3:8×0.3=2.4
Step 4:8×2=16
Add 0.03+0.2+2.4+16=18.63
Question 21.
Answer:Step 1:0.2×0.5=0.10
Step 2:
.2×9=1.8
Step 3:4×0.5=2
Step 4:4×9=36
Add 0.10+1.8+2+36=39.9
Question 22.
Answer:
Step1:0.6×0.8=0.48
Step2:0.6×6=3.6
Step3:7×0.8=5.6
Step4:7×6=42
Add 0.48+3.6+5.6+42=51.68
7.6×6.8=51.68
Question 23.
0.7 × 6.5 = ______
Answer:
Step1:0.7×0.5=0.35
Step2:0.7×6=4.2
Step3:0×0.5=0
Step4:0×6=0
Add 0.35+4.2=4.55
Therefore 0.7×6.5=4.55
Question 24.
25.6 × 16.9 = ______
Answer:
Step1:0.6×0.9=0.54
step2:0.6×16=9.6
Step3:25×0.9=22.5
Step4:25×16=400
Add 0.54+9.6+22.5+400=432.64
Therefore 25.6×16.9=432.64
Question 25.
2.5 × 6.81 = _____
Answer:
Step1:0.5×0.81=0.405
Step2:0.5×6=3
Step3:2×0.81=1.62
Step4:2×6=12
Add 0.405+3+1.62+12=17.025
Therefore 2.5×6.81=17.025
5.7 Use Strategies to Multiply Decimals
Find the product. Explain the strategy you used.
Question 26.
0.4 × 0.16 = ______
Answer:
Estimate
4×16
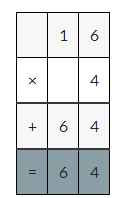
=64 place the decimal point before three places from the left
0.064
Therefore 0.4×0.16=0.064
Question 27.
0.2 × 0.8 = _______
Answer:
Estimate
2×8=16 and place the decimal point before two places from the left
0.16
Therefore 0.2×0.6=0.16
Question 28.
2.5 × 0.3 = ______
Answer:
Estimate
25×3
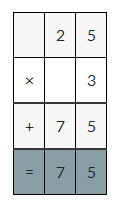
=74 and place the decimal point before two places from the left
0.74
Therefore 2.5×0.3=0.74
Question 29.
Structure
Your friend multiplies two decimals by rewriting the product as (8 × 3) × (0.1 × 0.1). What two decimals is she multiplying?
Answer:
(8×3)×(0.1×0.1)
(8×0.1)×(3×0.1)
0.8×0.3
The two decimals she is multiplying are 0.8 and 0.3
5.8 Multiply Decimals
Find the product.
Question 30.
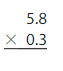
Answer:
Multiply 58 by 3 and place the decimal point
58×3
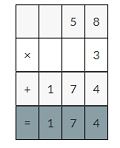
=174
Place the decimal point before two places from the left.
1.74
Therefore 5.8×0.3=1.74
Question 31.
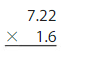
Answer:
Multiply 722 by 16 and place the decimal point
722×16
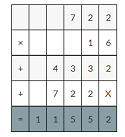
=11552
Place the decimal point before three places from the left
11.552
Therefore 7.22×1.6=11.552
Question 32.
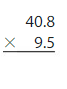
Answer:
Multiply 408 by 95 and place the decimal point
408×95
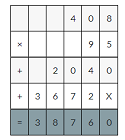
=38760
Place the decimal point before two places from the left
387.60
Therefore 40.8×9.5=387.60
5.9 Problem Solving: Multiply with Money
Question 33.
Your friend buys 4 glow sticks for $0.99 each. She pays with a $10 bill. How much change does she receive?
Answer:
My friend buys 4 glow sticks for $0.99 each
Total cost =4×$0.99=$3.96
Subtract cost from $10
$10‐$3.96=$6.04
change she receives is $6.04
Question 34.
Modeling Real Life
Descartes parks in the parking garage for 3 hours on Monday, 5 hours on Tuesday, and 10 hours on Wednesday. How much does he pay altogether?

Answer:
Descartes parks in the parking garage for 3 hours on Monday, 5 hours on Tuesday, and 10 hours on Wednesday.
parking garage rates are $4.50 per hour and $10.00 for more than 8 hours
charges on monday =3hoursx$4.50=$13.5
charges on tuesday =5hoursx$4.5=$22.5
on wednesday deacartes parks his car for more than 8 hours so, charges on wednesday are $10
Add 13.5+22.5+10=$46
Therefore Descartes pay $46 altogether.
Conclusion:
Take the help from the direct links available below and solve the problems covered in Big Ideas Math Answers Grade 5 Chapter 5 Multiply Decimals. Test your knowledge by solving the questions given at the end of the chapter. If you have any doubts regarding the concepts post the comments in the below attached comment box.