Have a glance at the Step by Step Big Ideas Math Book 4th Grade Chapter 12 Use Perimeter and Area Formulas Answer Key and get Homework help that you might need. Make the most out of the Big Ideas Math Answers Grade 4 Chapter 12 Use Perimeter and Area Formulas organized efficiently and clear all your queries during practice. We have provided the solution key of Big Ideas Math Grade 4 Chapter 12 Use Perimeter and Area Formulas in the pdf format so that you can prepare offline.
Big Ideas Math Book 4th Grade Answer Key Chapter 12 Use Perimeter and Area Formulas
Check out the topics covered in this chapter before you start your preparation. We provide simple methods to solve the problems in Big Ideas Math Book 4th Grade Answer Key Chapter 12 Use Perimeter and Area Formulas. If you stuck at some point you can go through the Bigideas Math Grade 4 Chapter 12 Use Perimeter and Area Formulas Solution Key. Just hit the links and clarify your doubts.
Lesson: 1 Perimeter Formula for a Rectangle
- Lesson 12.1 Perimeter Formula for a Rectangle
- Perimeter Formula for a Rectangle Homework & Practice 12.1
Lesson: 2 Area Formula for a Rectangle
Lesson: 3 Find Unknown Measures
Lesson: 4 Problem Solving: Perimeter and Area
- Lesson 12.4 Problem Solving: Perimeter and Area
- Problem Solving: Perimeter and Area Homework & Practice 12.4
Performance Task
- Use Perimeter and Area Formulas Performance Task 12
- Use Perimeter and Area Formulas Activity
- Use Perimeter and Area Formulas Chapter Practice
Lesson 12.1 Perimeter Formula for a Rectangle
Explore and Grow
Use color tiles to create a rectangle with a perimeter of 12 units. Compare your rectangle to your partner’s. How are they the same? How are they different?

How do you know that the perimeter of your rectangle is 12 units?
Answer:

The perimeter (P) of a rectangle = P=2l+2w( length=l ; width = w)
GIVEN: Perimeter of rectangle =12
P =2l + 2w
12= 2 (l + w)
12/2=l + w
6= l + w
Hence, the rectangle of my friend and mine are going to be same because perimeter given above is same for both the rectangle of us both.
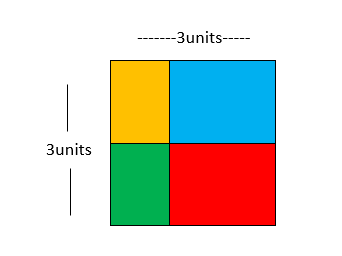
The rectangle of mine is having a length of 3 units and width of 3 units.
Perimeter of my rectangle= (2 x l) + (2 x w)
P=(2 x 3) + (2 x 3)
P= 6 + 6
P= 12 units.
Here, my rectangle has 12 units perimeter. This is how I know my rectangle is having 12 units as its perimeter.
Structure
How is the perimeter of a rectangle related to its length and width?
Answer:
The perimeter (P) of a rectangle is given by the formula, P=2l+2w , where “l” is the length and “w” is the width of the rectangle.
Think and Grow: Use a Formula for Perimeter
Perimeter is the distance around a figure. A formula is an equation that uses letters and numbers to show how quantities are related. You can use a formula to show how the length, width, and perimeter of a rectangle are related.
Example
Find the perimeter of the rectangle.
The length is ___ feet and the width is __ feet.
P = (2 × l) + (2 × W) Formula for perimeter of a rectangle
= (2 × ___) + (2 × ___)
= __ + __
= ___
The perimeter is ___ feet.
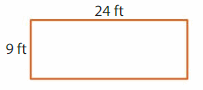
ANSWER:

Given: Length of Rectangle = 24 feet
Width of Rectangle = 9 feet
FORMULA: Perimeter = (2 x l) + (2 x w)
P = (2 x 24) + (2 x 9)
P = 48 + 18
P = 66 feet.
Hence, the Perimeter of the rectangle = 66 feet.
Show and Grow
Find the perimeter of the rectangle.
Question 1.
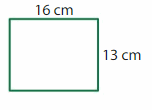
Answer:
GIVEN: Length of rectangle = 16cm
Width of rectangle = 13 cm
Perimeter of the rectangle = (2 x l) + (2 x w)
P = ( 2 x 16) + ( 2 x 13 )
P = 32 + 26
P = 58 cm.
Hence, the perimeter of the rectangle = 58 cm.
Question 2.
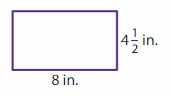
Answer:
GIVEN: Length of the rectangle = 8 inches
Width of the rectangle = 4 (1/2) inches =9/2 = 4.5 inches
Perimeter of the rectangle = (2 x l) + (2 x w) = 2( l + w)
P = 2( 8 + 4.5 )
P = 2(12.5 )
P = 25 inches.
Hence, the perimeter of the rectangle = 25 inches.
Apply and Grow: Practice
Find the perimeter of the rectangle.
Question 3.
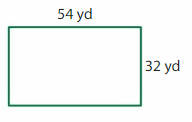
Answer:
GIVEN: Length of the rectangle = 54 yards
Width of the rectangle = 32 yards
Perimeter of the rectangle = (2 x l) + (2 x w) = 2( l + w)
P = 2(54+32)
P= 2 x 86
P= 172 yards.
Hence, the perimeter of the rectangle =172 yards.
Question 4.
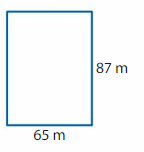
Answer:
GIVEN: Length of the rectangle =87 m
Width of the rectangle = 65 m
Perimeter of the rectangle = (2 x l) + (2 x w) = 2( l + w)
P= 2(87+65)
P= 2 x 153
P= 306 m.
Hence, the perimeter of the rectangle = 306 m.
Question 5.

Answer:
GIVEN: Length of the rectangle = 49 inches
Width of the rectangle = 18 inches
Perimeter of the rectangle = (2 x l) + (2 x w) = 2( l + w)
P = 2(49+18)
P =2 x 67
P =134 inches.
Hence, the perimeter of the rectangle = 134 inches.
Question 6.
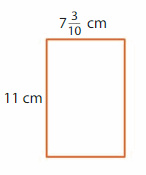
Answer:
GIVEN: Length of the rectangle =11 cm
Width of the rectangle = 7 (3/10) cm = 73/10 cm =7.3 cm
Perimeter of the rectangle = (2 x l) + (2 x w) = 2( l + w)
P = 2(11+7.3)
P = 2 x 18.3
P = 36.6 cm.
Hence, the perimeter of the rectangle = 36.6 cm.
Question 7.
You want to string lights around a rectangular room that is 12 feet long and 10 feet wide. How many feet of lights do you need?
Answer:
GIVEN: Length of the rectangle = 12 feet
Width of the rectangle = 10 feet
Perimeter of the rectangle = (2 x l) + (2 x w) = 2( l + w)
P = 2(12+10)
P = 2 x 22
P = 44 feet
Hence, 44 feet of light is needed..
Question 8.
YOU BE THE TEACHER
Your friend finds the perimeter of the rectangle. Is your friend correct? Explain.

p = (2 × 13) × (2 × 5)
= 26 × 10
= 260 ft
Answer: GIVEN: Length of the rectangle = 13 feet
Width of the rectangle = 5 feet
Perimeter of the rectangle = (2 x l) + (2 x w) = 2( l + w)
P = 2(13+5)
P = 2 x 18
P = 36 feet.
Hence, the perimeter of the rectangle = 36 feet.
Therefore my friend is wrong because his formula for finding perimeter of rectangle is wrong.
Perimeter of the rectangle = (2 x l) + (2 x w) = 2( l + w)
Question 9.
DIG DEEPER!
You can use the formula for the perimeter of a rectangle to find the perimeter of the square. What other formula can you use to find the perimeter of the square?

Answer:
The perimeter of a square is the total length of the four equal sides of the square.
Perimeter of the square = 4 × s = 4 s
The perimeter of a rectangle is the total length of the two lengths and two widths of the rectangle.
If the length and width of a rectangle are l and w, then its perimeter = 2(l + w) units.
We cannot equate the perimeter of a rectangle to find the perimeter of the square because rectangle has length and width whereas square has four sides.
No, other ways are there find the perimeter of the square.
Think and Grow: Modeling Real Life
Example
In a video game, you make a rectangular castle that is 4 times longer than it is wide. What is the perimeter of the castle?

Multiply 4 and the width of the castle to find the length.
4 × 25 = ___
The length of the castle is ___ yards.

Answer:
GIVEN: Width of the rectangular castle = 25 yards
Length of the rectangular castle = 4 times longer than it is wide =4 x 25 yards = 100 yards
Perimeter of the rectangle castle = (2 x l) + (2 x w) = 2( l + w)
P = 2 (100+25)
P = 2 x 125
P = 250 yards
Hence, Perimeter of the rectangle castle= 250 yards.
Show and Grow
Question 10.
A teacher wants to put a border around a rectangular whiteboard. The whiteboard is 2 times longer than it is wide. What is the perimeter of the whiteboard?

Answer:
GIVEN: Width of the rectangular castle = 1 m
Length of the rectangular castle = 2 times longer than it is wide = 2 x 1 m = 2 m
Perimeter of the rectangle castle= (2 x l) + (2 x w) = 2( l + w)
P = 2(2+1)
P = 2 x 3
P = 6 m
Hence, Perimeter of the rectangle castle = 6 m.
Question 11.
You want to put a ribbon border around each rectangular card. Which card requires more ribbon? How much more ribbon?

Answer:
GIVEN: FIRST RECTANGULAR CARD
Width of the rectangular card = 18 cm
Length of the rectangular card = 18 cm
Perimeter of the rectangle card= (2 x l) + (2 x w) = 2( l + w)
P = 2(18+18)
P = 2 x 36
P = 72 cm.
SECOND RECTANGULAR CARD
Width of the rectangular card = 14cm
Length of the rectangular card = 21 cm
Perimeter of the rectangle = (2 x l) + (2 x w) = 2( l + w)
P = 2(21+14)
P = 2 x 35
P = 70 cm.
The FIRST RECTANGULAR CARD needs the more ribbon than SECOND RECTANGULAR CARD because FIRST RECTANGULAR CARD Perimeter = 72 cm and SECOND RECTANGULAR CARD Perimeter = 70 cm.
That means difference in perimeter of FIRST RECTANGULAR CARD and the perimeter of SECOND RECTANGULAR CARD.
=72 cm – 70 cm
= 2 cm.
Question 12.
DIG DEEPER!
A rectangular flower bed has a length of 6 feet. The width is 48 inches shorter than the length. What is the perimeter of the flower bed?
Answer:
GIVEN:
Length of the rectangular bed = 6 feet
Width of the rectangular bed = 48 inches shorter than the length.
1 inch = 0.08333 feet
48inches = 48 x 0.0833 = 4 feet
Width of the rectangular bed = 4 feet
The perimeter of the rectangular flower bed = (2 x l) + (2 x w) = 2( l + w)
P = 2(6+4)
P = 2 x 10
P = 20 feet.
Hence, the perimeter of the rectangular flower bed = 20 feet.
Perimeter Formula for a Rectangle Homework & Practice 12.1
Find the perimeter of the rectangle.
Question 1.
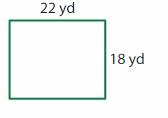
Answer:
GIVEN: Length of the rectangle = 22 yards
Width of the rectangle = 18 yards
Perimeter of the rectangle = (2 x l) + (2 x w) = 2( l + w)
P = 2(22+18)
P = 2 x 40
P = 80 yards.
Hence, the Perimeter of the rectangle = 80 yards.
Question 2.
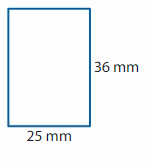
Answer:
GIVEN: Length of the rectangle = 36 mm
Width of the rectangle = 25 mm
Perimeter of the rectangle = (2 x l) + (2 x w) = 2( l + w)
P = 2(36+25)
P = 2 x 61
P =122 mm
Hence, the Perimeter of the rectangle = 122 mm.
Question 3.
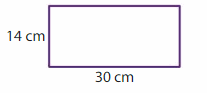
Answer:
GIVEN: Length of the rectangle = 30 cm
Width of the rectangle = 14 cm
Perimeter of the rectangle = (2 x l) + (2 x w) = 2( l + w)
P = 2(30+14)
P = 2 x 44
P = 88 cm
Hence, the Perimeter of the rectangle = 88 cm.
Question 4.
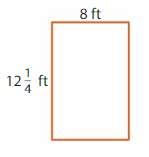
Answer:
GIVEN: Length of the rectangle = 12 (1/4) feet = 49/4 feet = 12.25 feet
Width of the rectangle = 8 feet
Perimeter of the rectangle = (2 x l) + (2 x w) = 2( l + w)
P = 2(12.25 + 8)
P = 2 x 20.25
P = 40.5 feet
Hence, the Perimeter of the rectangle = 40.5feet.
Question 5.
Number Sense
What is the perimeter of a square tabletop with side lengths of 48 inches?
Answer:
GIVEN: Side of the square tabletop = 48 inches
Perimeter of the square = 4 x sides
P = 4 x 48
P = 192 inches.
Hence, Perimeter of the square tabletop = 192 inches.
Question 6.
Structure
Use the Distributive Property to write P = (2 × l) + (2 × w) another way.
Answer:
According to the distributive property, multiplying the sum of two or more addends by a number will give the same result as multiplying each addend individually by the number and then adding the products together.
Perimeter of rectangle = (2 × l) + (2 × w)
P = 2(l + w)
Hence, According to distributive property, the another way of the Perimeter of rectangle = 2(l + w).
Question 7.
Open-Ended
Draw a rectangle that has the same perimeter as the one shown, but different dimensions.

Answer:
GIVEN: Length of the rectangle = 50 m
Width of the rectangle = 25 m
Perimeter of the rectangle = (2 x l) + (2 x w) = 2( l + w)
P = 2( 50+25)
P = 2 x 75
P = 150 m.
MY FIGURE:
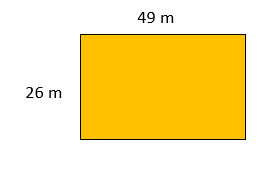
Length of the rectangle = 49m
Width of the rectangle = 26 m
Perimeter of the rectangle = (2 x l) + (2 x w) = 2( l + w)
P = 2( 49+26)
P = 2 x 75
P = 150 m.
Hence, the given rectangle Perimeter and my figure Perimeter are the same of 150 m.
Question 8.
Modeling Real Life
A worker places tape around a rectangular shipping label that is 2 times longer than it is wide. How much tape does the worker need?

Answer:
GIVEN:
Width of the rectangle shipping label = 74 mm
Length of the rectangle shipping label = 2 times longer than it is wide = 2 x 74mm = 148mm
Perimeter of the rectangle = (2 x l) + (2 x w) = 2( l + w)
P = 2(148+74)
P = 2 x 222
P = 444 mm.
Hence, Perimeter of the rectangle shipping label = 444 mm.
Question 9.
Modeling Real Life
A coach is painting lines around the perimeter of two rectangular fields. Which field requires more paint?

Answer:
GIVEN: FIRST A COACH
Length of the rectangle field A = 100yards
Width of the rectangle field A =65 yards
Perimeter of the rectangle field A= (2 x l) + (2 x w) = 2( l + w)
P = 2( 100+65)
P =2 x 165
P = 230 yards
Length of the rectangle field B = 120yards
Width of the rectangle field B =53 1/3 yards = 160/3 = 53.3 yards
P = (2 x l) + (2 x w) = 2( l + w)
P = 2( 120+53.3)
P = 2 x 173.3
P = 346.6 yards
Hence, Perimeter of the rectangle field B is more than Perimeter of the rectangle field A
=346.6 – 230 = 116.6 yards.
Therefore, Perimeter of the rectangle field A requires more 116.6 square yards than Perimeter of the rectangle field B.
Review & Refresh
Write the first six numbers in the pattern. Then describe another feature of the pattern.
Question 10.
Rule: Subtract 11.
First number: 99
Answer:
Rule: Subtract 11.
GIVEN: First number = 99 in the pattern
Second number = 99-11= 88
Third number = 88-11= 77
Fourth number = 77-11 = 66
Fifth number = 66-11 = 55
Sixth number = 55-11 =44
Another feature of this pattern is that all the numbers are multiples of table 11.
Question 11.
Rule: Multiply by 5.
First number: 5
Answer: Rule: Multiply by 5.
GIVEN: First number = 5 in the pattern
Second number = 5 x5 =25
Third number = 25 x 5 = 125
Fourth number = 125 x 5= 625
Fifth number = 625 x 5 = 3125
Sixth number = 3125 x 5 = 15625
Another feature of this pattern is that all the numbers are multiples of table 5.
Lesson 12.2 Area Formula for a Rectangle
Explore and Grow
Use color tiles to create a rectangle with an area of 12 square units. Compare your rectangle to your partner’s. How are they the same? How are they different?

How do you know that the area of your rectangle is 12 square units?
Answer:

Hence, the rectangle of my friend and mine are going to be same because area = 12 square units given above is same for both the rectangle of us both.
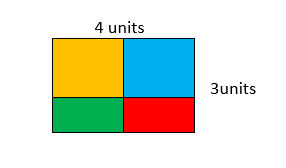
Area of the rectangle =l x w , where “l” is the length and “w” is the width.
Length of the rectangle = 4units
Width of the rectangle = 3units
A = l x w
A = 4 x 3
A = 12 square units.
Hence, the Area of the rectangle = 12 square units.
Structure
How is the area of a rectangle related to its length and width?
Answer:
The area “A” of a rectangle is given by the formula, A=l x w , where “l” is the length and “w” is the width.
Think and Grow: Use a Formula for Area
Area is the amount of surface a figure covers. You can use a formula to show how the length, width, and area of a rectangle are related.
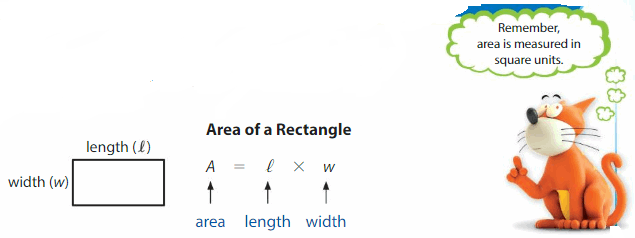
Example
Find the area of the rectangle.
The length is ___ inches and the width is ___ inches.
A = l × w Formula for area of a rectangle
= ___ × ___
= ___
The area is ___ square inches.

Answer:
GIVEN:
Length of the rectangle = 19 inches
Width of the rectangle = 14 inches
Area of the rectangle = l x w
A = 19 x 14
A = 266 square inches
Hence, the Area of the rectangle = 266 square inches.
Show and Grow
Find the area of the rectangle
Question 1.
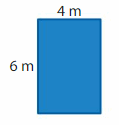
Answer:
GIVEN:
Length of the rectangle = 6 m
Width of the rectangle = 4 m
Area of the rectangle = l x w
A = 6 x 4
A = 24 square m.
Hence, the are of the rectangle = 24 square m.
Question 2.
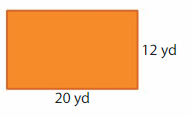
Answer:
GIVEN:
Length of the rectangle = 20 yards
Width of the rectangle = 12 yards
Area of the rectangle = l x w
A = 20 x 12
A = 240 square yards
Hence, the area of the rectangle = 240 square yards.
Question 3.
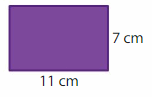
Answer:
GIVEN:
Length of the rectangle = 11 cm
Width of the rectangle = 7cm
Area of the rectangle = l x w
A = 11 x 7
A = 77 square cm
Hence, the area of the rectangle = 77 square cm.
Question 4.

Answer:
GIVEN:
Length of the rectangle = 5 feet
Width of the rectangle = 1 (1/2) feet = 3/2 feet = 1.5 feet
Area of the rectangle = l x w
A = 5 x 1.5
A = 7.5 square feet
Hence, the area of the rectangle = 7.5 square feet.
Apply and Grow: Practice
Find the area of the rectangle.
Question 5.
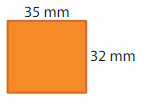
Answer:
GIVEN:
Length of the rectangle = 35 mm
Width of the rectangle = 32 mm
Area of the rectangle = l x w
A = 35 x 32
A = 1120 mm
Hence, the area of the rectangle = 1120 mm.
Question 6.

Answer:
GIVEN:
Length of the rectangle = 9 inches
Width of the rectangle = 4 (2/8) inches = 34/8 = 4.25 inches
Area of the rectangle = l x w
A = 9 x 4.25
A = 38.25 square inches
Hence, the area of the rectangle = 38.25 square inches.
Question 7.

Answer:
GIVEN:
Length of the rectangle = 8 feet
Width of the rectangle = 5 (1/2) feet =11/2 = 5.5 feet
Area of the rectangle = l x w
A = 8 x 5.5
A = 44 square feet
Hence, the area of the rectangle = 44 square feet.
Question 8.
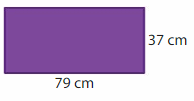
Answer:
GIVEN:
Length of the rectangle = 79 cm
Width of the rectangle = 37 cm
Area of the rectangle = l x w
A = 79 x 37
A = 2923 square cm
Hence, the area of the rectangle = 2923 square cm.
Question 9.
You are installing wall-to-wall carpet in a rectangular bedroom that is 10 feet long and 9 feet wide. How many square feet of carpet do you need?
Answer:
GIVEN:
Length of the wall-to-wall carpet in a rectangular bedroom = 10 feet
Width of the wall-to-wall carpet in a rectangular bedroom = 9 feet
Area of the rectangle = l x w
A = 10 x 9
A = 90 square feet.
Hence, the area of the wall-to-wall carpet in a rectangular bedroom = 90 square feet
Therefore, 90 square feet of carpet is need.
Question 10.
YOU BE THE TEACHER
Newton says the area of the rectangle is 33 square meters. Descartes says the area is 33 meters. Who is correct? Explain.

Answer:
Length of the rectangle = 11 m
Width of the rectangle = 3 m
Area of the rectangle = l x w
A = 11 x 3
A = 33 square m
The area of the rectangle is 33 square meters.
Hence, Newton says correct not Descartes.
Question 11.
DIG DEEPER!
Write a formula for the area of a square that has a side length of s. Then use your formula to find the area of the square shown.

Answer:
Area of the square = 4 x sides = 4 x s
Given : side of the square = 12 yards
Area of the square = 4 x sides = 4 x s
A= 4 x 12
A = 48 square yards
Hence, the Area of the square = 48 square yards.
Think and Grow: Modeling Real Life
Example
The length of the rectangular dance floor is 6 feet longer than the width. What is the area of the dance floor?
Add 6 feet to the width to find the length.

Answer:
GIVEN: Width of rectangular dance floor = 24 feet
Length of the rectangular dance floor = 6 feet longer than the width = 24 +6 = 30 feet
Area of the rectangular dance floor = l x w
A = 30 X 24
A = 720 square feet
Hence, the Area of the rectangular dance floor = 720 square feet.
Show and Grow
Question 12.
A designer creates a rectangular advertisement for a website. The length of the advertisement is 1\(\frac{1}{2}\) centimeters longer than the width. What is the area of the advertisement?

Answer:
Length of the rectangular advertisement = 1\(\ frac {1}{2}\) centimeters longer than the width= 1(1 /2) cm + 7 cm = =3 / 2 cm + 7 cm = (1.5 + 7 )cm =8.5 cm
Width of the rectangular advertisement = 7 cm
Area of the rectangular advertisement = l x w
A = 8.5 x 7
A = 59.5 cm
Hence, the Area of the rectangular advertisement = 59.5 cm.
Question 13.
You create a mural using 4 rectangular posters that are each 4\(\frac{1}{4}\) feet long and 2 feet wide. You put the posters next to each other with no gaps or overlaps. What is the area of the mural?
Answer:
GIVEN:
Width of the rectangular posters= 2 feet
Length of the rectangular posters= 4\(\frac{1}{4}\) feet = 4 (1/4) feet = 17/4 feet = 4.25 feet
Area of the mural = l x w
A = 4.25 x 2
A = 8.5 square feet
Hence, the Area of the mural = 8.5 square feet.
Question 14.
DIG DEEPER!
Two rolls of wrapping paper have the same piece. The red roll is 3 feet wide and is 10 yards long when unrolled. The striped roll is 3\(\frac{1}{2}\) feet wide and 8 yards long when unrolled. Which roll is the better buy? Explain.
Answer:
GIVEN:
Width of Red roll =3 feet
CONVERTION : 1 YARD = 3 FEET
Width of Red roll =3 feet = 1 yard
Length of the red roll = 10 yards
Area of the red roll = l x w
A = 10 x 1
A = 10 square yards.
Area of the red roll = 10 square yards.
Width of striped roll = 3\(\frac{1}{2}\) feet = 3 1/2 feet = 3.5 feet.
CONVERTION : 1 YARD = 3 FEET
Width of striped roll = 3.5 feet
I yard = 3.5 feet
Width of striped roll = yard = 3.5 / 1 feet
Width of striped roll = 3.5 yard
Length of striped roll = 8 yards
Area of the striped roll = l x w
A = 3.5 x 8
A = 28 square yards.
Area of the striped roll = 28 square yards.
Its better to buy striped roll than red roll because u are going to get more.
Area Formula for a Rectangle Homework & Practice 12.2
Find the area of the rectangle
Question 1.
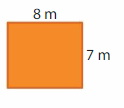
Answer:
GIVEN: Length of the rectangle = 8 m
Width of the rectangle = 7 m
Area of the rectangle = l x w
A = 8 x 7
A = 42 square m
Hence, Area of the rectangle = 42 square m.
Question 2.
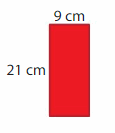
Answer:
GIVEN: Length of the rectangle = 21 cm
Width of the rectangle = 9 cm
Area of the rectangle = l x w
A = 21 x 9
A = 189 square cm
Hence, Area of the rectangle = 189 square cm.
Question 3.

Answer:
GIVEN: Length of the rectangle = 56 yards
Width of the rectangle = 12 yards
Area of the rectangle = l x w
A = 56 x 12
A = 672 square yards
Hence, Area of the rectangle = 672 square yards.
Question 4.
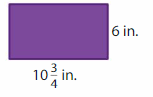
Answer:
GIVEN:
Length of the rectangle = 10 (3/4) inches = 43/4 = 10.75 inches
Width of the rectangle = 6 inches
Area of the rectangle = l x w
A = 10.75 x 6
A = 64.5 square inches
Hence, Area of the rectangle = 64.5 square inches.
Question 5.
What is the area of the window?

Answer:
GIVEN:
Length of the window = 48 inches
Width of the window = 18 inches
Area of the window = l x w
A = 48 x 18
A = 864 square inches
Hence, the Area of the window = 864 square inches.
Question 6.
Structure
A rectangle has an area of 40 square feet. The dimensions are whole numbers. What are all of the possible dimensions of the rectangle?
Answer:
GIVEN:
Area of the rectangle = 40 square feet.
The whole numbers are the part of the number system in which it includes all the positive integers from 0 to infinity. These numbers exist in the number line.
Area of the rectangle = l x w
All of the possible dimensions of the rectangle =
40 =1 × 40
40 = 2 × 20
40 = 4 × 10
40 = 5 × 8.
Question 7.
Open-Ended
Draw a rectangle that has the same area as the one shown, but different dimensions.
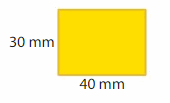
Answer:
GIVEN:
Length of the rectangle = 40 mm
Width of the rectangle = 30 mm
Area of the rectangle = l x w
A = 40 x30
A = 1200 mm
Area of the rectangle = 1200 mm.
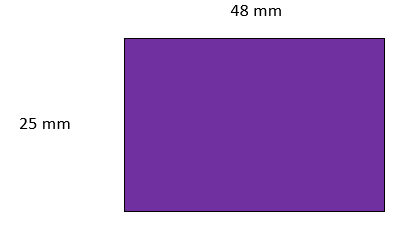
Length of my rectangle = 48 mm
Width of my rectangle = 25 mm
Area of my rectangle = l x w
A = 48 x 25
A = 1200 mm
Hence, the Area of my rectangle = 1200 mm.
Question 8.
Modeling Real Life
An interior designer says that a rug under a dining room table should be 4 feet longer and 4 feet wider than the table. What is the area of a rug a customer should buy for under the table?
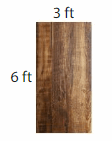
Answer:
GIVEN:
Length of the dinning table = 6 feet
Width of the dinning table = 3feet
AS PER DESIGNER THE DINNING TABLE REQUIRED DIMENSIONS ARE AS BELOW:
Length should be 4 feet longer than table.
Length of the dinning table= 6 feet
Length of the rug = 6 feet + 4 feet = 10 feet
Width should be 4 feet wider than the table.
Width of the dinning table = 3feet
Width of the rug = 3 feet + 4 feet = 7 feet
Area of the rug = l x w
A = 10 x 7
A = 70 square feet.
Hence, the Area of the rug = 70 square feet.
Question 9.
DIG DEEPER!
A wolf hunts within a rectangular area that is 10 miles long and 5 miles wide. A cougar hunts within a rectangular area that is 8 miles long and 6 miles wide. Which animal hunts within a greater area? How much more area does the animal hunt in?
Answer:
GIVEN:
Length of the wolf hunts rectangular area=10 miles
Width of the wolf hunts rectangular area=5 miles
Area the wolf hunts rectangular area= l x w
A = 10 x 5
A = 50 square miles.
Area the wolf hunts rectangular area= 50 square miles.
Length of the cougar hunts rectangular area= 8 miles
Width of the cougar hunts rectangular area= 6 miles
Area of the cougar hunts rectangular area= l x w
A = 8 x 6
A = 48 square miles
Area of the cougar hunts rectangular area= 48 square miles.
Hence, wolf hunts within a greater area than the cougar hunts.
Area the wolf hunts rectangular area= 50 square miles.
Area of the cougar hunts rectangular area= 48 square miles.
DIFFERENCE:
Area the wolf hunts rectangular area – Area of the cougar hunts rectangular area
= 50 square miles – 48 square miles
= 2 miles.
Therefore, Wolf hunts more of 2 square miles area than the cougar hunts.
Review & Refresh
Find the quotient.
Question 10.
70 ÷ 7 = __
Answer:
70 ÷ 7 = 10.
The quotient of 70 ÷ 7 = 10.
Question 11.
420 ÷ 6 = ___
Answer:
420 ÷ 6 = 70.
The quotient of 420 ÷ 6 = 70.
Question 12.
2,400 ÷ 8 = ___
Answer:
2,400 ÷ 8 = 300.
The quotient of 2,400 ÷ 8 = 300.
Lesson 12.3 Find Unknown Measures
Explore and Grow
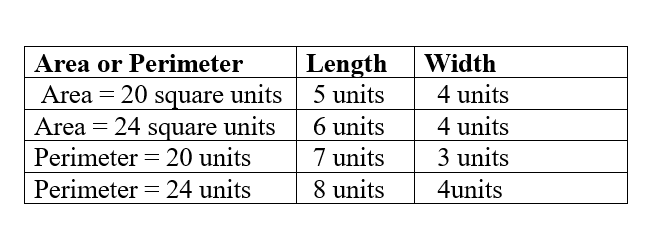
For each row of the table, use color tiles to create the rectangle described. Then complete the table.
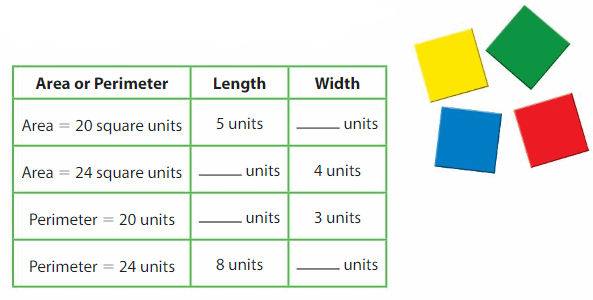
Answer:
GIVEN:

Area of the rectangle = 20 square units
length of the rectangle = 5 units
Width of the rectangle = ??
Let the Width of the rectangle be W
Area of the rectangle = l x w
=> 20 square units = 5units x W
=> 20 / 5 = W
=> 4 units =W
Width of the rectangle = 4 units
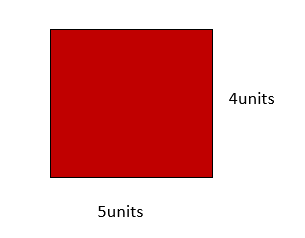
GIVEN:
Area of the rectangle = 24 square units
Length of the rectangle = ??
Let the Length of the rectangle = l
Width of the rectangle = 4 units
Area of the rectangle = l x w
=> 24 square units = l x 4units
=> 24 / 4= l
=> 6 units =l
Length of the rectangle = 6 units
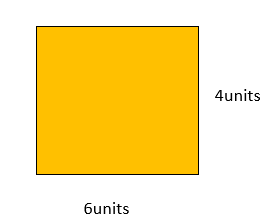
GIVEN:
Perimeter of the rectangle = 20 units
Length of the rectangle = ??
Let the length of the rectangle be l
Width of the rectangle = 3 units
Perimeter of the rectangle = 2l x 2w = 2 (l + w)
20 = 2(l+ 3)
20 / 2= L + 3
10 = l + 3
10 – 3 =l
l =7 units.
The Length of the rectangle = 7 units.
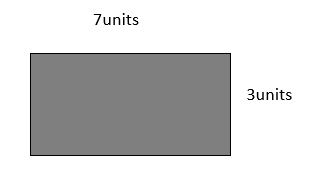
GIVEN:
Perimeter of the rectangle = 24 units
Length of the rectangle = 8 units
Width of the rectangle = ??
Let the Width of the rectangle = w
Perimeter of the rectangle = 2l x 2w = 2 (l + w)
24 = 2 ( 8 + w)
24/2 =8 + w
12 = 8 + w
12 – 8 = w
w = 4units
Width of the rectangle = 4units.

The required table is as below:
Reasoning
Compare your strategy to your partner’s. How are they the same or different?
Answer:
The strategy of mine and my partner does not vary as both the required answers value is same.
Think and Grow : Find Unknown Measures
Example
The area of the rectangle is 36 square feet. Find the length.

Answer:
GIVEN:
Area of the rectangle = 36 square feet.
Length of the rectangle = l feet
Width of the rectangle = 3 feet
Area of the rectangle = l x w
36 = l x 3
36/3 = l
12 feet = l
Hence, the Length of the rectangle =12 feet
Example
The perimeter of the rectangle is 30 centimeters. Find the width.

Answer:
GIVEN:
Perimeter of the rectangle = 30 centimeters.
Length of the rectangle = 8 cm
Width of the rectangle = w cm
Perimeter of the rectangle = (2 x l) + ( 2 x w )
30 = ( 2 x 8) + (2 x w)
30 = 16 + 2w
30 – 16 = 2w
14 = 2w
14/2 = w
7 = w
Hence, the Width of the rectangle = 7 cm.
Show and Grow
Question 1.
Area = 75 square meters

Answer:
GIVEN:
Area of the rectangle = 75 square meters
Length of the rectangle = l m
Width of the rectangle = 5 m
Area of the rectangle = l x w
75 = l x 5
75/5 = l
15 = l
Hence, the length of the rectangle = 15 m.
Question 2.
Perimeter = 42 inches
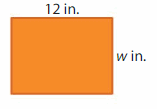
Answer:
GIVEN:
Perimeter of the rectangle = 42 inches
Length of the rectangle = 12 inches
Width of the rectangle = w inches
Perimeter of the rectangle = (2 x l) + ( 2 x w ) = 2 ( l + w )
Hence, the Width of the rectangle = 3.5 inches.
Apply and Grow: Practice
Find the unknown measure of the rectangle.
Question 3.
Area = 50 square millimeters

Answer:
GIVEN:
Area of the rectangle = 50 square millimeters
Length of the rectangle = l mm
Width of the rectangle = 2 mm
Area of the rectangle = l x w
50 = l x 2
50/2 = l
25 = l
Hence, the length of the rectangle = 25 mm.
Question 4.
Perimeter = 30 centimeters
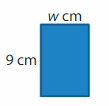
Answer:
GIVEN:
Perimeter of the rectangle = 30 centimeters
Length of the rectangle = 9 cm
Width of the rectangle = w cm
Perimeter of the rectangle = (2 x l) + ( 2 x w ) = 2 ( l + w )
30 = 2( 9+w )
30/2 = 9 + w
15 = 9 + w
15 – 9 = w
6 = w
Hence, the width of the rectangle = 6 cm.
Question 5.
Area = 240 square meters
![]()
Answer:
GIVEN:
Area of the rectangle = 240 square meters
Length of the rectangle = 80 m
Width of the rectangle = w m
Area of the rectangle = l x w
240 = 80 x w
240/80 = w
3 = w
Hence, the Width of the rectangle = 3 m.
Question 6.
Perimeter = 86 yards
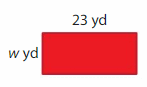
Answer:
GIVEN:
Perimeter of the rectangle = 86 yards
Length of the rectangle = 23 yards
Width of the rectangle = w yards
Perimeter of the rectangle = (2 x l) + ( 2 x w ) = 2 ( l + w )
86 = 2( 23 + w)
86/2 = 23 +w
43 = 23 + w
43 – 23 = w
20 = w
Hence, the Width of the rectangle = 20 yards.
Question 7.
Perimeter 44 2/4 inches

Answer:
GIVEN:
Perimeter of the rectangle = 44 (2/4) inches = 90/4 = 22.5 inches
Length of the rectangle = l inches
Width of the rectangle = 8 (1/4) inches = 33/4 = 8.25 inches
Perimeter of the rectangle = (2 x l) + ( 2 x w ) = 2 ( l + w )
22.5 = 2( l+ 8.25)
22.5/2 = l + 8.25
11.25 = l + 8.25
11.25 – 8.25 = l
3.00 = l
Hence, the Length of the rectangle = 3 inches.
Question 8.
Area = 108 square feet
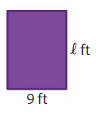
Answer:
GIVEN:
Area of the rectangle = 108 square feet
Length of the rectangle = l feet
Width of the rectangle = 9 feet
Area of the rectangle = l x w
108 = l x 9
108/9 = l
12 = l
Hence, the Length of the rectangle = 12 feet.
Question 9.
DIG DEEPER!
What are the dimensions of Newton’s rectangle?

Answer:
Area of the Newton’s rectangle = 24 square meters
Let the Width of the Newton’s rectangle be w m.
Length of the Newton’s rectangle = 2 meters longer than the width = 2 + w
Area of the Newton’s rectangle = l x w
Factors of 24:
1 x 24 = 24 => 1 x ( 1 + 2 ) = 1 x 3= 3
2 x 12 = 24 =>2 x (2+2) =2 x 4 =8
3 x 8 = 24 =>3 x (3+2) = 3 x 5 = 15
4 x 6 = 24 => 4 x (4+2) = 4 x 6 = 24
The dimensions of Newton’s rectangle:
Width of the Newton’s rectangle = 4 m
Length of Newton’s rectangle = 4 + 2= 6 m
CHECK:
Area of of Newton’s rectangle =l x w
A = 4 x 6
A = 24 square meters.
Hence , the The dimensions of Newton’s rectangle = 4 m and 6 m.
Question 10.
DIG DEEPER!
The area of a square is 81 square centimeters. What is the perimeter of the square?
Answer:
GIVEN:
Area of a square = 81 square centimeters.
Area of a square =s2
81 = s2
√ 81 = s
9 = s
Side of the square = 9 cm
Perimeter of the square = 4x s
P= 4 x 9
P = 36 cm.
Hence, Perimeter of the square = 36 cm.
Think and Grow: Modeling Real Life
Example
The rectangular park has an area of 200 square yards. You kick a soccer ball straight across the width of the park. How far did you kick the soccer ball?
Use a formula to find the width.

Answer:
GIVEN:
Area of the rectangular park =200 square yards
Length of the rectangular park = 25 yards
Width of the rectangular park =w yards
Area of the rectangular park = l x w
200 = 25 x w
200/25 = w
8 = w
Hence, the Width of the rectangular park =9 yards.
Therefore, the soccer kicks the ball 8 yards far in the rectangular park.
Show and Grow
Question 11.
The rectangular parking spot has an area of 220 square feet. What is the length of the longest car that can fit in the parking spot?
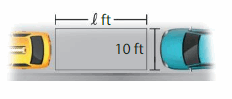
Answer:
GIVEN:
Area of the rectangular parking spot = 220 square feet
Width of the rectangular parking spot = 10 feet
Length of the rectangular parking spot = l feet
Area of the rectangular parking spot = l x w
220 = l x 10
220/10 = l
22 = l
Hence, the Length of the rectangular parking spot = 22 feet.
Therefore , the length of the longest car that can fit in the parking spot is 22 feet.
Question 12.
You want to put a frame around the rectangular painting. The painting has a perimeter of 50 inches. How wide should the frame be?
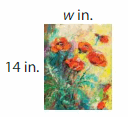
Answer:
GIVEN:
Perimeter of the rectangular painting frame= 50 inches
Length of the rectangular painting frame= 14 inches
Width of the rectangular painting frame= w inches
Perimeter of the rectangular painting = 2l + 2w = 2( l + w)
50 = 2(14+w)
50/2 = 14 + w
25 = 14 + w
25 – 14 =w
11 = w
Hence, the Width of the rectangular painting frame= 11 inches.
Question 13.
A rectangular zoo enclosure for a red panda has a perimeter of 116 meters. The length is 50 meters. What is the area of the enclosure?
Answer:
GIVEN:
Perimeter of the rectangular zoo = 116 meters
Length of the rectangular zoo = 50 meters
Width of the rectangular zoo = ??
Let the Width of the rectangular zoo = w meters
Perimeter of the rectangular painting = 2l + 2w = 2( l + w)
116 = 2( 50+ w)
116/2 = 50 + w
58 = 50 + w
58 – 50 = w
8 = w
Hence, the Width of the rectangular zoo = 8 meters
Area of the rectangular zoo =??
Area of the rectangular zoo = l x w
A = 50 x 8
A = 400 square meters
Therefore, the Area of the rectangular zoo = 400 square meters.
Question 14.
DIG DEEPER!
A rectangular patio at a restaurant has an area of 98 square feet. The dimensions of the patio are whole numbers. The length of the patio is 2 times the width. What are the dimensions of the patio?
Answer:
GIVEN:
Area of the rectangular patio = 98 square feet.
The dimensions of the patio are whole numbers.
The length of the patio is 2 times the width.
Let the Width of the rectangular patio be w feet.
=> Length of the the rectangular patio = 2 x w = 2w
Area of the rectangular patio = l x w
98 = (2w) x w
98 = 2w2
98/2 = w2
49 = w2
√ 49 = w
7 = w
Hence, the Width of the rectangular patio = 7 feet.
Length of the the rectangular patio = 2 x w = 2w= 2 x 7 = 14 feet
Therefore, the dimensions of the patio are 14 feet and 7 feet.
Find Unknown Measures Homework & Practice 12.3
Find the unknown measures of the rectangle.
Question 1.
Area = 63 square feet
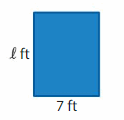
Answer:
GIVEN:
Area of the rectangle = 63 square feet
Length of the rectangle = l feet
Width of the rectangle = 7 feet
Area of the rectangle = l x w
63 = l x 7
63/7 = l
9 = l
Hence, the Length of the rectangle = 9 feet.
Question 2.
Perimeter = 26 yards

Answer:
GIVEN:
Perimeter of the rectangle = 26 yards
Length of the rectangle = l yard
Width of the rectangle = 1 yard
Perimeter of the rectangle = 2l + 2w = 2 ( l + w)
26 = 2( l + 1)
26/2 = l +1
13 = l + 1
13 – 1 = l
12 = l
Hence, the Length of the rectangle = 12 yards.
Find the unknown measure of the rectangle.
Question 3.
Perimeter = 40 centimeters
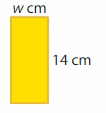
Answer:
GIVEN:
Perimeter of the rectangle = 40 centimeters
Length of the rectangle =14 cm
Width of the rectangle = w cm
Perimeter of the rectangle = 2l + 2w = 2 ( l + w)
40 = 2( 14 + w)
40/2 =14 + w
20 = 14 + w
20 – 14= w
6 = w
Hence, the Width of the rectangle = 6 cm.
Question 4.
Area = 88 square millimeters
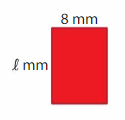
Answer:
GIVEN:
Area of the rectangle = 88 square millimeters
Length of the rectangle = l mm
Width of the rectangle = 8 mm
Area of the rectangle = l x w
88 = l x 8
88/8 = l
11 = l
Hence , the Length of the rectangle = 11 mm.
Question 5.
Area = 2,800 square meters
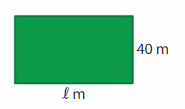
Answer:
GIVEN:
Area of the rectangle = 2,800 square meters
Length of the rectangle = l m
Width of the rectangle = 40 m
Area of the rectangle = l x w
2800 = l x 40
2800/40 = l
70 = l
Hence, the Length of the rectangle = 70 m.
Question 6.
Perimeter = 41 inches
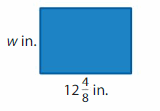
Answer:
GIVEN:
Perimeter of the rectangle = 41 inches
Length of the rectangle =12 (4/8) inches = 100/8 = 12.5 inches
Width of the rectangle = w inches
Perimeter of the rectangle = 2l + 2w = 2 ( l + w)
41 = 2( 12.5 +w)
41/2 =12.5 + w
20.5 = 12.5 + w
20.5 – 12.5 = w
8 = w
Hence, the Width of the rectangle = 8 inches.
Question 7.
Structure
A rectangle has an area of 18 square inches and a perimeter of 18 inches. What are the dimensions of the rectangle?
Answer:
GIVEN:
Area of the rectangle = 18 square inches
Perimeter of the rectangle =18 inches.
LET, the Length of the rectangle be l inches
The Width of the rectangle be w inches.
FORMULA:
Area of the rectangle = l x w
18 = l x w
The dimensions of the rectangle :
18 = 1 x 18
18 = 2 x 9
18 = 3 x 6
Hence, the dimensions of the rectangle are (1,18);(2,9);(3,6) inches.
Question 8.
Modeling Real Life
The rectangular fire pit has a perimeter of 176 inches. What is the width of the fire pit?

Answer:
GIVEN :
Perimeter of the rectangular fire pit = 176 inches
Length of the rectangular fire pit = 50 inches
Width of the rectangular fire pit = ??
Let the Width of the rectangular fire pit be w inches.
Perimeter of the rectangular fire pit = 2l + 2w = 2(l + w)
176 = 2( 50 + w)
176/2 = 50 + w
88 = 50 + w
88 – 50 = w
35 = w
Hence, the Width of the rectangular fire pit = 35 inches.
Question 9.
A painting canvas has an area of 384 square inches. The length and width of the canvas are whole numbers. The length of the canvas is 8 inches greater than the width. What are the dimensions of the canvas?
Answer:
GIVEN:
Area of the painting canvas = 384 square inches.
The length of the canvas is 8 inches greater than the width.
Let the Width of the painting canvas be w inches.
Area of the painting canvas = l x w => 384 = l x w
384 = 1x 384 =>1 x (1 + 8) = 1 x 9 = 9
384 = 2 x 192 =>2 x (2+8) = 2 x 10 = 20
384 = 3 x 128 => 3 x (3 + 8) = 3 x 11 = 33
384 = 4 x 96 => 4 x (4 + 8) = 4 x 12 = 48
384= 6 x 64 => 6 x (6 + 8) = 6 x 14 = 84
384 = 8 x 48 => 8 x (8 + 8) =8 x 16 = 128
384 =12 x 32 =>12 x (12 + 8) = 12 x 20 = 240
384 =16 x 24 => 16 x (16 +8) = 16 x 24 = 384
Hence, The dimensions of the canvas= (24,16) inches
Length of the canvas = 24 inches
Width of the canvas = 16 inches
Review & Refresh
Find the equivalent length.
Question 10.
35 ft = __ in.
Answer:
CONVERTION: 1 feet = 12 inches
35 feet = ?? inches
Let the unknown value be Y inches.
=>35 x 12 = 1 x Y
=>420 = 1 x Y
=> 420/1 = Y
=> 420 = Y
Hence, the unknown value = 420 inches.
35 feet = _420_ inches.
Question 11.
6 mi = __ yd
Answer:
CONVERTION: 1 mile =1760 yard
6 miles = ?? yard
Let the unknown value be X yards.
=> 1 x X = 1760 x 6
=> 1X = 10560
=> X = 10560/1
=> X = 10560
Hence, the unknown value be 10560 yards.
6 mi = _10560_ yd
Question 12.
17 yd = __ ft
Answer:
CONVERTION:
1 yard = 3 feet
17 yd = ?? feet
Let the unknown value be X feet.
=>1 x X = 3 x 17
=>1X = 51
=>X = 51/1
=> X = 51 feet
Hence, the unknown value be 51 feet.
17 yd = _51_ ft
Question 13.
4 yd = __ in.
Answer:
CONVERTION:
1 yard = 36 inches
4 yards = ?? inches
Let the unknown value be Y inches.
=> 1 x Y = 36 x 4
=> 1Y = 144
=> Y = 144/1
=> Y = 144
Hence, the unknown value be 144 inches.
4 yd = _144_ in.
Lesson 12.4 Problem Solving: Perimeter and Area
Explore and Grow
An office has a large rectangular window overlooking a city. Describe two methods for finding the area of the rectangular wall around the window.

Answer:
GIVEN:
Area of the inside window = l x w
Area of the outside wall = l x w
Area of the rectangular wall around the window = area of the outside wall – Area of the inside window
Hence, there is only one way to find the Area of the rectangular wall around the window.
Make Sense of Problems
Use one of your methods to estimate the area of a wall with a window.
Answer:
The area of the wall can be estimated to be twice the area of the window.
Think and Grow: Problem Solving: Perimeter and Area
Example
A rectangular board has an area of 1,700 square inches. You cut out a rectangular piece that is 10 inches long and 9 inches wide to make a carnival prop similar to the one shown. What is

Answer:
GIVEN:
Area of rectangular board =1,700 square inches
Length of the rectangular piece cut = 10 inches
Width of the rectangular piece cut = 9 inches
Area of the rectangular piece cut = l x w
=>A = 10 X 9
=> A = 90 square inches
Area of the rectangular piece cut = 90 square inches.
Subtract Area of the cut out piece you cut out from the original area.
= 1700 square inches – 90 square inches
= 1610 square inches.
Hence, the Area of the area of the prop = 1610 square inches.
Understand the Problem
What do you know?
- The original board has an area of 1,700 square inches.
- The piece you cut out is 10 inches long and 9 inches wide.
What do you need to find?
- You need to find the area of the carnival prop.
Make a Plan
How will you solve?
- Find the area of the piece you cut out.
- Subtract the area of the piece you cut out from the original area.
Solve
Step 1: Find the area of the piece you cut out.
Step 2: Subtract the area of the you cut out piece you cut out from the original area.
![]()
The area of the prop is __ square inches.
Answer:
Area of rectangular board =1,700 square inches
Length of the rectangular piece cut = 10 inches
Width of the rectangular piece cut = 9 inches
Area of the rectangular piece cut = l x w
=>A = 10 X 9
=> A = 90 square inches
Area of the rectangular piece cut = 90 square inches.
Subtract Area of the cut out piece you cut out from the original area.
= 1700 square inches – 90 square inches
= 1610 square inches.
Hence, the Area of the area of the prop = 1610 square inches
Show and Grow
Question 1.
Explain how you can check whether your answer above is reasonable.
Answer:
My above answer is reasonable because it satisfies.
Area of the area of the prop + Area of the cut out piece =The Area of the outside rectangular
=>1610 square inches + 90 square inches
=>1700 square inches.
Hence, proved my answer is reasonable and correct.
Apply and Grow: Practice
Understand the problem. What do you know? What do you need to find? Explain.
Answer:
GIVEN:
Area of rectangular board =1,700 square inches
Length of the rectangular piece cut = 10 inches
Width of the rectangular piece cut = 9 inches
This is known in the problem.
You need to find the area of the carnival prop.
Question 2.
A construction worker has 40 feet of caution tape. Is this enough tape to surround a rectangular region that is 120 inches long and 90 inches wide?
Answer:
GIVEN:
A construction worker has 40 feet of caution tape.
Length of the rectangular region = 120 inches
Width of the rectangular region = 90 inches
Perimeter of the rectangular region = 2l + 2 w = 2( l + w)
P = 2( 120 + 90)
P = 2 x 210
P = 420 inches.
CONVERTION: 1 inch = 0.8333 feet or (1/12) feet
420 inches = ??
Let the unknown value be X feet
=> 1 x X = 420 x 1/12
=> 1X = 420/12
=> 1X = 35 feet.
The required tape to surround the rectangular region = 35 feet.
A construction worker has 40 feet of caution tape.
Therefore, the tape of construction worker bought will be enough to surround a rectangular region that is 120 inches long and 90 inches wide.
Question 3.
One ton of salt de-ices a rectangular section of a road that is 10,500 meters long and 3 meters wide. How many square meters does 6 tons of salt de-ice?
Answer:
GIVEN:
One ton of salt de-ices a rectangular section of a road
Length of the One ton of salt de-ices rectangular section of a road = 10500 meters
Width of the One ton of salt de-ices rectangular section of a road = 3 meters
Area of the One ton of salt de-ices rectangular section of a road = l x w
A = l x w
A = 10500 x 3
A = 31500 square meters
Area of the One ton of salt de-ices rectangular section of a road = 31500 square meters.
Area of the 6 ton of salt de-ices rectangular section of a road = ??
Area of the 6 ton of salt de-ices rectangular section of a road = (Area of the one ton of salt de-ices rectangular section of a road) x 6
=> 31500 x 6
=> 189000 square feet.
Therefore, Area of the 6 ton of salt de-ices rectangular section of a road = 189000 square feet.
Understand the problem. Then make a plan. How will you solve? Explain.
Question 4.
A worker installs fencing around two rectangular properties. One is 99 feet long and 80 feet wide. The other is95 feet long and 83 feet wide. Which property requires more fencing? How much more?
Answer:
GIVEN:
A worker installs fencing around two rectangular properties.
ONE RECTANGULAR PROPERTY
Length of the one rectangular property = 99 feet
Width of the one rectangular property = 80 feet
Perimeter of the one rectangular property = 2l + 2w = 2( l + w)
P = 2 ( 99+ 80 )
P = 2 x 179
P = 358 feet
Perimeter of the one rectangular property = 358 feet.
OTHER RECTANGULAR PROPERTY
Length of the other rectangular property = 95 feet
Width of the other rectangular property = 83 feet
Perimeter of the other rectangular property = 2l + 2w = 2( l + w)
P = 2 ( 95 + 83 )
P = 2 x 178
P = 356 feet
Perimeter of the other rectangular property = 356 feet
DIFFERENCE:
Perimeter of the one rectangular property – Perimeter of the other rectangular property
=> 358 – 356
=> 2 feet.
One rectangular property requires more fencing than the other rectangular property.
Therefore, 2 feet more it requires than the one rectangular property than the other rectangular property.
Question 5.
A roofer covers the rectangular roof with shingles. A chimney occupies a rectangular area that is 4 feet long and 2 feet wide. How many square feet of the roof are with shingles?

Answer:
GIVEN:
A roofer covers the rectangular roof with shingles.
Length of the rectangular area of chimney = 4 feet
Width of the rectangular area of chimney = 2 feet
Area of the rectangular area of chimney = l x w
A = 4 x 2
A = 8 square feet
Area of the rectangular area of chimney = 8 square feet.
Length of the rectangular roof = 60 feet
Width of the rectangular roof= 30 feet
Area of the rectangular roof = l x w
A = 60 x 30
A = 1800 square feet
Area of the rectangular roof = 1800 square feet.
Area of the roof are with shingles = Area of the rectangular roof – Area of the rectangular area of chimney
=> 1800 square feet – 8 square feet
=> 1792 square feet.
Area of the roof are with shingles = 1792 square feet.
Question 6.
You want to buy a cover for the lid of your laptop. Your laptop is 1\(\frac{1}{3}\) feet long and 1 foot wide. Which cover will fit best on your laptop?
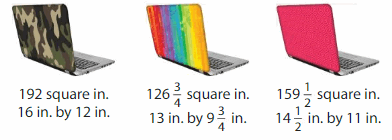
Answer:
GIVEN:
Length of the Laptop = 1\(\frac{1}{3}\) feet long =1 (1/3) feet = 4/3 feet = 1. 33 feet.
Width of the laptop = 1 feet
Perimeter of the laptop =2l + 2w = 2( l + w)
P = 2( 1.33 + 1)
P =2 x 2.33
P = 4.66 feet
Perimeter of the laptop =4.66 feet.
CONVERTION:
1 feet = 12 inches
4.66 feet =??
=> 4.66 x 12
=> 55.92 inches
Hence, the perimeter of the laptop = 55.92 inches.
FIRST LAPTOP COVER :
Length of the first Laptop cover = 16 inches
Width of the first Laptop cover = 12 inches
Area of the first Laptop cover = 192 square inches
Perimeter of the first Laptop cover = 2l + 2w = 2( l + w)
P = 2( 16 + 12)
P = 2 x 28
P = 56 inches.
Perimeter of the first Laptop cover = 56 inches.
SECOND LAPTOP COVER :
Length of the second Laptop cover = 13 inches
Width of the second Laptop cover = 9 (3/4)inches = 39/4 inches = 9.75 inches
Area of the second Laptop cover = 126 (3/4) square inches
Perimeter of the second Laptop cover = 2l + 2w = 2( l + w)
P = 2( 13 +9.75 )
P = 2 x 22.75
P = 45.5 inches.
Perimeter of the second Laptop cover = 45.5 inches.
THIRD LAPTOP COVER
Length of the third Laptop cover = 14 (1/2) inches = 29/2 inches= 14.5 inches
Width of the third Laptop cover = 11 inches
Area of the third Laptop cover = 159 (1/2) square inches
Perimeter of the third Laptop cover = 2l + 2w = 2( l + w)
P = 2( 14.5 + 11 )
P = 2 x 25.5
P = 51 inches.
Perimeter of the third Laptop cover = 51 inches.
Therefore, first laptop cover will fit correctly to the laptop because cover size is more accurate size of 56 inches than other two laptop covers are lesser in size of the laptop size 55.92 inches.
Think and Grow: Modeling Real Life
Example
A worker wants to cover the miniature golf putting surface with artificial turf. The putting surface is in the shape of two rectangles. How much turf does the worker need?
Think: What do you know? What do you need to find? How will you solve?
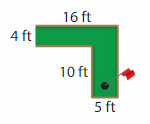
Step 1: Divide the surface into two rectangles. Then find the area of each rectangle.
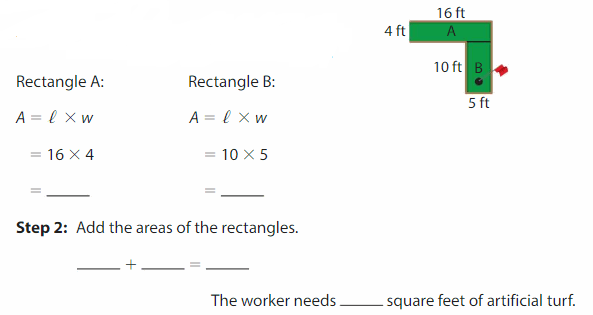
Answer:
GIVEN:

Divide the surface into two rectangles. Then find the area of each rectangle.
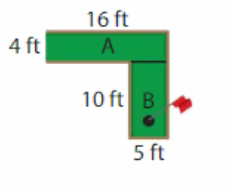
Length of the Rectangle A = 16 feet
Width of the Rectangle A = `4 feet
Area of the Rectangle A = l x w
A =16 x 4
A = 64 square feet
Area of the Rectangle A = 64 square feet.
Length of the Rectangle B = `10 feet
Width of the Rectangle B = `5 feet
Area of the Rectangle B = l x w
A = 10 x 5
A = 50 square feet
Area of the Rectangle B = 50 square feet.
ADDITION:
Area of the Rectangle A + Area of the Rectangle B
=> 64 square feet + 50 square feet
=> 114 square feet.
Hence, the workers need 114 square feet for artificial turf.
Question 7.
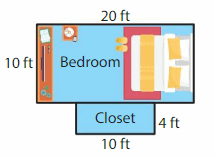
You want to install new carpet in the rectangular bedroom and the rectangular closet. How much carpet do you need to cover the floor?
Answer:
GIVEN:

Length of the rectangular bedroom = 20 feet
Width of the rectangular bedroom = 10 feet
Area of the rectangular bedroom = l x w
A = 20 x 10
A = 200 square feet
Area of the rectangular bedroom = 200 square feet.
Length of the rectangular closet = 10 feet
Width of the rectangular closet= 4 feet
Area of the rectangular closet = l x w
A = 10 x 4
A = 40 square feet
Area of the rectangular closet = 40 square feet.
ADDITION:
Carpet needed to cover the floor = Area of the rectangular bedroom + Area of the rectangular closet.
=> 200 square feet + 40 square feet
=> 240 square feet.
Hence, the Carpet needed to cover the floor = 240 square feet.
Question 8.
A gardener wants to enclose the garden with fencing. The garden is in the shape of two rectangles. How much fencing does the gardener need?

Answer:

Divide the surface into two rectangles.

Length of the Rectangle A = 8 yard
Width of the Rectangle A = 6 yard
Perimeter of the Rectangle A = 2l x 2w = 2( l + w)
P = 2( 8 + 6 )
P = 2 x 14
P = 28 yards
Perimeter of the Rectangle A = 28 yards.
Length of the Rectangle B = 10 yard
Width of the Rectangle B = 3 yard
Perimeter of the Rectangle B = 2l x 2w = 2( l + w)
P = 2( 10 + 3 )
P = 2 x 13
P = 26 yards
Perimeter of the Rectangle B = 26 yards.
Fencing the gardener needed = Perimeter of the Rectangle A + Perimeter of the Rectangle B
=> 28 yards + 26 yards
=> 54 yards.
Hence, the Fencing the gardener needed = 54 yards.
Problem Solving: Perimeter and Area Homework & Practice 12.4
Understand the problem. Then make a plan. How will you solve? Explain.
Question 1.
An indoor dog park has an area of 50,000 square feet. The owner creates a square welcome center inside the park that is 100 feet long. What is the area of the section that dogs can play in?
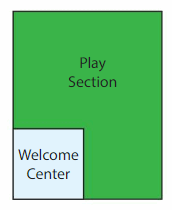
Answer:
GIVEN:

Area of the indoor dog park = 50,000 square feet.
The owner creates a square welcome center inside the park that is 100 feet long.
=> side of the square welcome center inside the park = 100 feet
Area of the square welcome center inside the park = s x s
A = 100 x 100
A = 10,000 square feet
Area of the square welcome center inside the park = 10,000 square feet.
Area of the section that dogs can play in = Area of the indoor dog park – Area of the square welcome center inside the park
=> 50,000 square feet – 10,000 square feet
=> 40,000 square feet.
Hence, the Area of the section that dogs can play in = 40,000 square feet.
Question 2.
You tile a hallway with square tiles that are 12 inches wide. You completely cover the hallway with 3 rows of 5 tiles. What is the area of the hallway?
Answer:
GIVEN:
Side of the square tiles = 12 inches
The hallway completely covered with 3 rows of 5 tiles.
Area of the square tiles hallway= s x s
A = 12 x 12
A = 144 square inches.
Hence, the Area of the square tiles hallway= 144 square inches.
Question 3.
Your friend makes a rectangular poster for a school play. The poster is 4 feet long and 3 feet wide. Ribbon costs $1 per foot. How much does it cost to add a ribbon border to the poster?
Answer:
GIVEN:
Length of the rectangular poster = 4 feet
Width of the rectangular poster = 3 feet
Perimeter of the rectangular poster = 2l +2w = 2(l + w)
P = 2 ( 4 + 3 )
P = 2 x 7
P = 14 feet
Perimeter of the rectangular poster = 14 feet.
Ribbon costs $1 per foot
Cost of the ribbon border to the poster = 14 feet x $1= $14
Therefore, the Cost of the ribbon border to the poster = $14.
Question 4.
Writing
Explain how you know when you need to find the perimeter or the area of a rectangle when solving a word problem.
Answer:
GIVEN:
Perimeter can be thought as the length of the outline of a shape.
Area can be defined as the space occupied by a flat shape or the surface of an object.
On the above referred points, I try to calculate the perimeter or the area of the rectangle when solving a word problem.
Question 5.
Modeling Real Life
Your teacher joins two rectangular tables for students to complete a craft. How much newspaper does your teacher need to cover the tops of the tables with no overlap and no paper hanging over the sides?
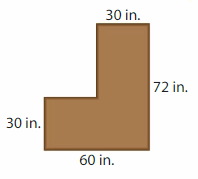
Answer:
GIVEN:

Divide the surface into two rectangles.
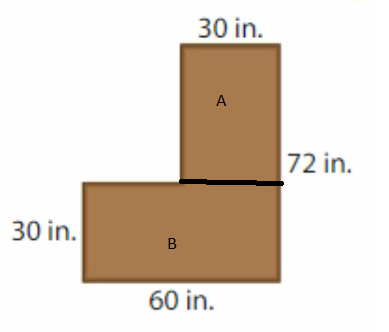
Length of the rectangle A = 72 inches
Width of the of the rectangle A = 30 inches
Perimeter of the rectangle A = 2l + 2w = 2( l + w)
P = 2( 72 + 30 )
P = 2 x 102
P = 204 inches
Perimeter of the rectangle A = 204 inches.
Length of the rectangle B = 60 inches
Width of the of the rectangle B = 30 inches
Perimeter of the rectangle B = 2l + 2w = 2( l + w)
P = 2( 60 + 30 )
P = 2 x 90
P = 180 inches
Perimeter of the rectangle B = 180 inches.
Newspaper needed to cover the tops of the tables with no overlap and no paper hanging over the sides = Perimeter of the rectangle A + Perimeter of the rectangle B
= 204 inches + 180 inches
= 384 inches.
Hence, the newspaper needed to cover the tables = 384 inches.
Question 6.
Modeling Real Life
A landscaper buys 2 bags of grass seed. Each bag covers 5,000 square feet. A rectangular lawn is 200 feet long and 40 feet wide. Does the landscaper have enough seed to cover the lawn once? twice? Explain.
Answer:
GIVEN:
A landscaper buys 2 bags of grass seed.
Area of the bags seed covers = 5000 square feet.
Length of the rectangular lawn = 200 feet
Width of the rectangular lawn = 40 feet
Area of the rectangular lawn = l x w
A = 200 x 40
A = 8000 square feet.
Area of the rectangular lawn = 8000 square feet.
The landscaper have enough seed to cover the lawn once only not twice because he has bags which can cover only 5000 square feet not 8000 square feet rectangular lawn completely.
Review & Refresh
Multiply
Question 7.
![]()
Answer:
GIVEN:
![]() = 2 x 1/4
= 2 x 1/4
= 1 x 1/2
= 1/2
= 0.5
Hence, 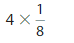 = 0.5.
= 0.5.
Question 8.
![]()
Answer:
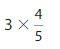 = 12/5
= 12/5
= 2.4.
Hence, 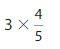 = 2.4.
= 2.4.
Question 9.
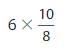
Answer:
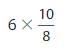 = 6 x 5/4
= 6 x 5/4
= 3 x 5/2
=15/2
= 7.5.
Hence, 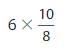 = 7.5.
= 7.5.
Use Perimeter and Area Formulas Performance Task 12
Stop-motion animation videos are made by taking multiple photographs of an object. Each photograph shows the object in a slightly different position. When all of the photographs are combined into a video, the object appears to be moving.

1. You decide to make a stop-motion video. You make a background with an area of 12 square feet and a perimeter of 14 feet.
a. What are the dimensions of your background?
b. The part of the background in each photograph is 45 inches long and 30 inches wide. What is the perimeter of the background in each photograph?
c. What is the area of the background that is not in each photograph?
2. You take photographs for your video. Your video shows 15 photographs each second. How many photographs are in a 24-second video?
3. You start working on your animation at 3:05 P.M. and finish at 5:20 P.M. You spend equal amounts of time creating your background, taking photographs, and editing your video. How much time do you spend on each activity?
Answer:
GIVEN:
Area of the rectangular background= 12 square feet.
Perimeter of the rectangular background = 14 feet.
1. a) All dimensions of the rectangular background =
Area of the rectangle = l x w
1 × 12 = 12.
2 × 6 = 12.
3 × 4 = 12.
The dimensions of the rectangular background = (1,12); (2,6);(3,4).
b) The Length of the background in each photograph = 45 inches The Width of the background in each photograph =30 inches The perimeter of the background in each photograph = 2l + 2w = 2(l + w)
P = 2 (45 + 30)
P = 2 x 75
P = 150 inches.
Hence, the perimeter of the background in each photograph = 150 inches.
2)
GIVEN:
15 photograph taken in 1 second
=> ?? in 24 seconds
=> 24 x 15 = photographs taken in 24 seconds
=> 360 = photographs taken in 24 seconds
Hence, photographs taken in 24 seconds = 360.
3)
GIVEN:
Starting time on animation at 3:05 P.M.
Finishing time on animation at 5:20 P.M.
Time taken on each activity = Finishing time on animation – Starting time on animation
=> 5:20 P.M – 3:05 P.M
=> 2: 15 Hours
Hence, Time taken on each activity =2:15 Hours.
Use Perimeter and Area Formulas Activity
Area Roll and Conquer
Directions:
- Players take turns rolling two dice.
- On your turn, create a rectangle with the numbers on the dice as the length and width. Your rectangle cannot cover another rectangle.
- Shade the rectangle in your color. Record the multiplication equation for the rectangle.
- If you cannot create a rectangle on the board, then you lose your turn. Play 10 rounds, if possible.
- The player with the greatest area covered wins!
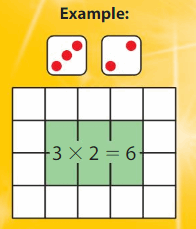

Answer:
GIVEN:
- Players take turns rolling two dice.
1) 
2)

Length of the rectangle = 4 units
Width of the rectangle = 3 units.
3) 
Equation of the rectangle = 4 x 3 = 12 square units.
4)
 5)
5)
The player with the greatest area covered wins!
Given Equation Area = 3 x 2 = 6 square units
My Equation Area= 4 x 3 =12 square units
Use Perimeter and Area Formulas Chapter Practice
12.1 Perimeter Formula for a Rectangle
Find the perimeter of the rectangle.
Question 1.
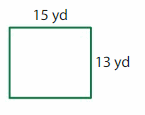
Answer:
GIVEN:
Length of the rectangle = 15 yard
Width of the rectangle = 13 yard
Perimeter of the rectangle = 2l + 2w = 2( l + w)
P = 2 (15 + 13)
P = 2 x 28
P = 56 yards
Hence, the Perimeter of the rectangle = 56 yards.
Question 2.
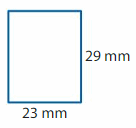
Answer:
GIVEN:
Length of the rectangle = 29 mm
Width of the rectangle = 23 mm
Perimeter of the rectangle = 2l + 2w = 2( l + w)
P = 2 ( 29 + 23)
P = 2 x 52
P = 104 mm
Hence, the Perimeter of the rectangle = 104 mm.
Question 3.
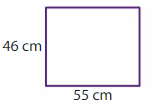
Answer:
GIVEN:
Length of the rectangle = 55 cm
Width of the rectangle = 46 cm
Perimeter of the rectangle = 2l + 2w = 2( l + w)
P = 2( 55 + 46)
P = 2 x 101
P = 202 cm
Hence, the Perimeter of the rectangle = 202 cm.
Question 4.
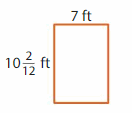
Answer:
GIVEN:
Length of the rectangle = 10 (2/12) feet = 20/12 = 1.67 feet
Width of the rectangle = 7 feet
Perimeter of the rectangle = 2l + 2w = 2( l + w)
P = 2(1.67 + 7)
P = 2 x 7.67
P = 15.34 feet
Hence, the Perimeter of the rectangle = 15.34 feet.
12.2 Area Formula for a Rectangle
Find the area of the rectangle.
Question 5.
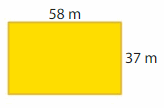
Answer:
GIVEN:
Length of the rectangle = 58 m
Width of the rectangle = 37 m
Area of the rectangle = l x w
A = 58 x 37
A = 2146 square m.
Hence, the Area of the rectangle = 2146 square m.
Question 6.
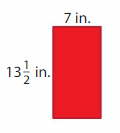
Answer:
GIVEN:
Length of the rectangle = 13 (1/2) inches = 27/2 = 13.5 inches
Width of the rectangle = 7 inches
Area of the rectangle = l x w
A = 13.5 x 7
A = 94.5 square inches
Hence, the Area of the rectangle = 94.5 square inches.
Question 7.
A rectangle has an area of 60 square feet. The dimensions are whole numbers. What are all of the possible dimensions of the rectangle?
Answer:
GIVEN:
Length of the rectangle = l feet
Width of the rectangle = w feet
Area of the rectangle = 60 square feet
Area of the rectangle = l x w
All possible dimensions of rectangle =
60 = 1 x 60,
60 = 2 x 30,
60 = 3 x 20,
60 = 4 x 15
60 = 5 x 12,
60 = 6 x 10.
All possible dimensions of rectangle =(1,60);(2,30);(3,20);(4,15);(5,12);(6,10).
12.3 Find Unknown Measures
Find the unknown measure of the rectangle.
Question 8.
Area = 48 square yards
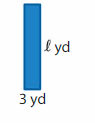
Answer:
GIVEN:
Area of the rectangle = 48 square yards
Length of the rectangle = l yards
Width of the rectangle = 3 yards
Area of the rectangle = l x w
48 = l x 3
48/3 = l
16 = l
Hence, the Length of the rectangle = 16 yards.
Question 9.
Perimeter = 90 centimeters
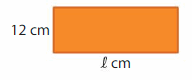
Answer:
GIVEN:
Perimeter of the rectangle = 90 centimeters
Length of the rectangle = l cm
Width of the rectangle = 12 cm
Perimeter of the rectangle = 2l + 2w = 2( l + w)
90 = 2( l + 12)
90/2 = l + 12
45 = l + 12
45 – 12 = l
33 = l
Hence, the Length of the rectangle = 33 cm.
Question 10.
Logic
What are the dimensions of Descartes’s rectangle?

Answer:
GIVEN:
Perimeter of the rectangle = 10 meters
Length and Width have a product = 6 square meters
=> l x w = 6 square meters
=> Area of the rectangle = l x w = 6 square meters.
All possible dimensions of the rectangle =
6 = 1 x 6
6 = 2 x 3.
Hence, All possible dimensions of the rectangle =(1,6);(2,3).
12.4 Problem Solving: Perimeter and Area
Question 11.
Modeling Real Life
You want to paint the wall. What is the area of the wall you will paint?
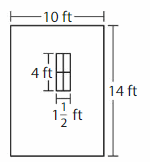
Answer:
GIVEN:
Length of the outer rectangle = 14 feet
Width of the outer rectangle = 10 feet
Area of the outer rectangle = l x w
A = 14 x 10
A = 140 square feet.
Area of the outer rectangle = 140 square feet.
Length of the inside rectangle = 4 feet
Width of the inside rectangle = 1(1/2) feet = 3/2 = 1.5 feet
Area of the inside rectangle = l x w
A = 4 x 1.5
A = 6 square feet.
Area of the inside rectangle = 6 square feet.
SUBTRACTION:
Area of the wall for paint = Area of the outer rectangle – Area of the inside rectangle
= 140 square feet – 6 square feet.
= 134 square feet.
Hence, the Area of the wall for paint = 134 square feet.
Question 12.
A park director orders 360 feet of fencing. Does he have enough to surround the tennis court?
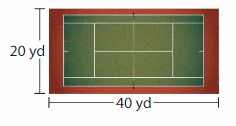
Answer:
GIVEN:
Fencing length park director ordered = 360 feet.
Length of the rectangle = 40 yards
Width of the rectangle = 20 yards
Perimeter of the rectangle = 2l + 2w = 2 ( l + w)
P= 2( 40 + 20)
P = 2 x 60
P = 120 yards
CONVERTION:
1 yard = 3 feet
120 yards = ??
=> 120 x 3
=> 360 feet.
Hence, the director ordered fencing 360 feet is enough for fencing the tennis court because the required court perimeter is same 360 feet.
Conclusion:
I wish the information provided in the Big Ideas Math Answers Grade 4 Chapter 12 Use Perimeter and Area Formulas is helpful for you all. Share the pdf links with your friends and help them to overcome the difficulties in maths. If you any doubts feel free to post the comments in the below-mentioned comment box. Bookmark our page to get the updates of Big Ideas Math Grade 4 Answer Key for all Chapters.