Quick and easy learning of measurements in maths is possible with our ccss math answers. You can get the best study material on this page. Download Big Ideas Math Answers Grade 4 Chapter 11 Understand Measurement Equivalence for free of cost. You can learn the metric units of length, mass, capacity, units of times, customary units of length, capacity here.
Big Ideas Math Book 4th Grade Answer Key Chapter 11 Understand Measurement Equivalence
The students who are in search of solutions of 4th std can get them on Big Ideas Math Answers Grade 4 Chapter 11 Understand Measurement Equivalence. Learn the different methods to solve the problems in Big Ideas Math Book 4th Grade Answer Key Chapter 11 Understand Measurement Equivalence. We have provided the solutions as per the topics in the below sections. Hence click on the links and kickstart your preparation.
Lesson: 1 Length in Metric Units
Lesson: 2 Mass and Capacity in Metric Units
- Lesson 11.2 Mass and Capacity in Metric Units
- Mass and Capacity in Metric Units Homework & Practice 11.2
Lesson: 3 Length in Customary Units
Lesson: 4 Weight in Customary Units
Lesson: 5 Capacity in Customary Units
Lesson: 6 Make and Interpret Line Plots
Lesson: 7 Units of Time
Lesson: 8 Problem Solving: Elapsed Time
Lesson: 9 Mixed Measures
Performance Task
- Understand Measurement Equivalence Performance Task
- Understand Measurement Equivalence Activity
- Understand Measurement Equivalence Chapter Practice
- Understand Measurement Equivalence STEAM Performance Task
Lesson 11.1 Length in Metric Units
Explore and Grow
Work with a partner. Find 3 objects in your classroom, and use a meter stick to measure them. One of you measure in centimeters, and the other measure in millimeters. Think: What do you notice about the pairs of measurements? How does each measurement compare to1 meter?
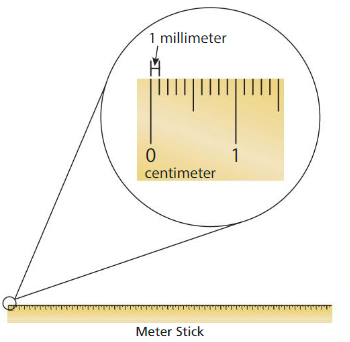
1 centimeter is 10 times as long as 1 millimeter.
1 meter is 100 times as long as 1 centimeter.
1 meter is 1000 times as long as 1 millimeter.
Structure
You know the length of an object in centimeters. Without measuring, how can you find its length in millimeters?
Answer:
Think and Grow: Find Equivalent Metric Lengths
Metric units of length include, centimeters, meters, millimeters and kilometers.

Example
Find the number of meters in 3 kilometers.
There are 1000 meters in 1 kilometer.
3 ×1000 =3000
So, there are meters in 3 kilometers.
Example
Find the number of millimeters in 9 meters.

There are 100 centimeters in 1 meter.
9 ×100 = 9 centimeters
There are 10 millimeters in 1 centimeter.
900 × 10= 9000 millimeters
So, there are 9000 millimeters in 9 meters..
Show and Grow
Find the equivalent length.
Question 1.
8 km = ________ m
Answer:
8 km = 8000 m
Explanation:
one kilometer is 1000 times as long as 1 meter
8 x 1000 m = 8000 m
So, there are 8000 meters in 8 km.
Question 2.
7 m = ________ cm
Answer:
7 m= 700 cm
Explanation:
The meter is unit of length in the metric system equivalent to one hundred centimeters.
7×100 = 700cm
so, there are 700 cm in 7 m.
Question 3.
5 cm = ________mm
Answer:
5 cm = 50 mm
Explanation:
The centimeter is unit of length in the metric system equivalent to 10 millimeters.
5×10 =50 mm
so, there are 50 mm in 5 cm.
Question 4.
6 km = ________cm
Answer:
6 km = 600000 cm
Explanation:
1 km is equal to 1000 meters and one meter is equal to100 centimeters.
step 1: 6×1000=6000
step 2: 6000×100=600000
Apply and Grow: Practice
Find the equivalent length.
Question 5.
3 cm =_______mm
Answer:
3 cm = 30mm
Explanation:
The centimeter is unit of length in the metric system equivalent to ten millimeters.
3 x 10=30mm
Question 6.
8 m = _______cm
Answer :
8 m = 800cm
Explanation:
The meter is unit length in the metric system equivalent to 100 centimeters.
8×100=800cm
Question 7.
9 cm = ______mm
Answer:
9 cm = 90mm
Explanation:
The centimeter is unit of length in the metric system equivalent to 10 millimeters.
9×10=90mm
Question 8.
4 m = _______ cm
Answer:
4 m = 400 cm
Explanation :
one meter is equal to 100 centimeter
4×100=400cm.
so, there are 400cm in 4m.
Question 9.
11 km = ________m
Answer:
11 km = 11000m
Explanation:
one kilometer is equal to 1000 meters
11×1000=11000m
so, there are 11000 m in 11 km.
Question 10.
2 km = ________ cm
Answer:
2 km = 200000 cm
Explanation:
one kilometer is equal to 1000 meters and one meter is equal to 100centimeters
2×1000=2000m
2000×100=200000cm
Question 11.
3 m = ______mm
Answer:
3 m = 3000mm
Explanation:
one meter is equal to 100 centimeter and one centimeter is equal to 10 millimeters
3×100=300
300×10=300mm.
Question 12.
5 km = ______m
Answer:
5 km = 5000m
Explanation:
one kilometer is equal to 1000 meters
5×1000=5000m.
Question 13.
A pencil is 19 centimeters long. How many millimeters long is the pencil?
Answer:
The centimeter is unit of length in the metric system equivalent to 10 millimeters.
19×10=190mm long pencil.
Question 14.
Number Sense
How does the meaning of each prefix relate to the metric units of length in this lesson?
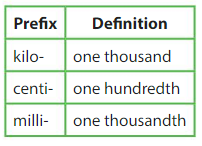
Answer:
one kilo is equal to one thousand meter
one centi is equal to hundredth of a meter
one milli is equal to thousandth of a meter.
DIG DEEPER!
Compare.
Question 15.

Answer:
4 meters is equal to 400 cm
Explanation:
one meter is equal to 100 cm
4 x 100 =400cm
Question 16.

Answer:
5000mm is not equal to 50m
Explanation:
5000mm is equal to 5m.
Think and Grow: Modeling Real Life
Example
During 1 day of swim practice, your friend swam12,600 meters. Your friend’s goal was to swim 2\(\frac{1}{2}\) kilometers. Did he reach his goal?

Make a table that shows the relationship between kilometers and meters.
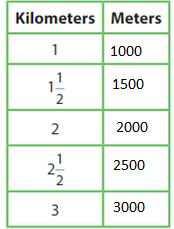
Compare 2,600 meters to 2 \(\frac{1}{2}\) kilometers.
Answer:
2×1/2=2500
Your friend did not reach his goal.
Show and Grow
Question 17.
You have 42 millimeters of wire. You need 4\(\frac{1}{2}\) centimeters of wire to make an earring. Do you have enough wire to make the earring?
Answer: Yes,
Explanation:
The wire is 42 mm, we needed the wire for making earrings which is in cm we have to convert that in to mm.
one cm =10 mm
1cm =10mm
4 ×1/2 =9/2
= 4.5 ×10
=45 centimeters
Question 18.
Which insect’s wingspan is longer? How much longer is it?
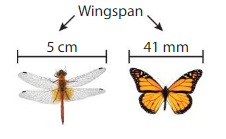
Answer:
5cm wing span is longer because 1 cm =10mm
Question 19.
DIG DEEPER!
There are signs posted every 500 meters along a 5-kilometer race. How many signs are posted?

Answer:
10 signs
Explanation:
1 signs are posted for every 500 meters
1 km=1000m
so, there are 10 signs for 5 km.
Length in Metric Units Homework & Practice 11.1
Find the equivalent length.
Question 1.
3 km = ___ m
Answer:
3 km = 8000 m
Explanation:
one kilometer is 1000 times as long as 1 meter
3 x 1000 m = 3000 m
So, there are 3000 meters in 8 km.
Question 2.
5 m = _____ mm
Answer:
5 m = 5000mm
Explanation:
one meter is 1000 times as long as 1000 millimeter
5 x 1000 m = 5000 mm
So, there are 5000millimeters in 5 m.
Question 3.
12 km = ____ m
Answer:
12 km = 12000 m
Explanation:
one kilometer is 1000 times as long as 1 meter
12 x 1000 m = 12000 m
So, there are 12000 meters in 12 km.
Question 4.
8 m = _____ cm
Answer:
8 meters is equal to 400 cm
Explanation:
one meter is equal to 100 cm
8 x 100 =800cm
Question 5.
9 km = ____ cm
Answer:
9 km = 900000 cm
Explanation:
one kilometer is equal to 1000 meters and one meter is equal to 100centimeters
9×1000=9000m
9000×100=900000cm
Question 6.
6m = _____ mm
Answer:
6 m=6000mm
Explanation:
one meter is equal to 100 cm
one cm is equal to 10 millimeter
6m x 100 =600cm
600×10=6000mm
Question 7.
7 m = ____ cm
Answer:
7 m=700cm
Explanation:
one meter is equal to 100cm
7 x 100= 700cm
Question 8.
4 m = ____ mm
Answer:
4m = 4000mm
Explanation:
one meter is equal to 100 centimeter
one centimeter is equal to 10 mm
4 x 100 = 400cm
400 x 10 = 4000mm.
Question 9.
A basketball player is 2 meters tall. How tall is the player in centimeters?
Answer:
200cm
Explanation:
The basketball player is 2m tall,one meter is equal to 100 cm
2 x 100 =200cm
so, the player is 200cm.
Question 10.
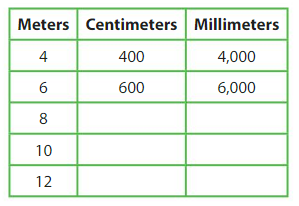
Which One Doesn’t Belong?
Which measurement does not belong with the other three?
50 m
500 km
5,000 cm
50,000 mm
Answer:
500 km
Question 11.
Patterns
Describe and complete the pattern.
Answer:
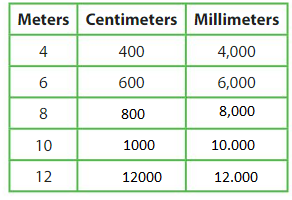
Explanation:
one meter is equal to 100 cm and that is equal to 100mm.
Question 12.
Modeling Real Life
A pencil is 190 millimeters long. A pencil box 1is 20\(\frac{1}{2}\) centimeters long. Will the pencil fit inside the pencil box?
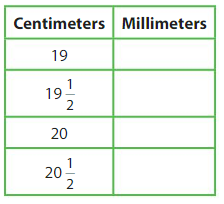
Answer:
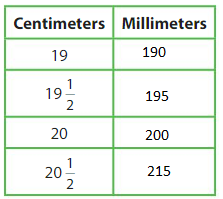
215 m long.
Explanation:
one centimeter is equal to 10mm, A pencil is 190 cm is long and the pencil box is 215 cm long it can easily fit in the box.
Question 13.
DIG DEEPER!
An airplane runway is 4 kilometers long. An airplane starts at one end and travels 2,044 meters. How many more meters can the airplane travel before reaching the end of the runway?

Answer:
1956meters
Explanation:
The airplane started and travelled 2044 m
total it has to travel is 4 km
one kilometer is equal to 1000m
4000-2044 =1956m
Review & Refresh
Find the factor pairs for the number.
Question 14.
11
Answer: 1,11
One of two or more numbers or expressions that are multiplied to obtain a given product
Question 15.
25
Answer: 1,5,25
One of two or more numbers or expressions that are multiplied to obtain a given product
Question 16.
12
Answer: 1,3,4,12.
One of two or more numbers or expressions that are multiplied to obtain a given product
Lesson 11.2 Mass and Capacity in Metric Units
Explore and Grow
Use a balance and weights to help you complete the statement.
1 kilogram is 1000 times as much as 1 gram.
Use a 1-liter beaker to help you complete the statement.
1 liter is 1000 times as much as 1 milliliter.

Structure
You know the mass of an object in kilograms. Without using a scale, how can you find its mass in grams?
Answer with the help of :weighing machine
Think and Grow: Find Equivalent Metric Measures
Metric units of mass include grams and kilograms.

Metric units of capacity include liters and milliliters.

Example
Find the number of grams in 3 kilograms.
There are 1000 grams in 1 kilogram.
3 ×1000 = 3000
So, there are 3000 grams in 3 kilograms.
Example
The container holds 5 liters of water. How many milliliters of water does the container hold?

There are 1000 milliliters in 1 liter.
5 ×1000= 5000
So, the container holds 5000 milliliters of water.
Show and Grow
Find the equivalent mass.
Question 1.
6 kg = _______g
Answer:
6 kg = 6000g
Explanation:
There are 1000 grams in 1 kilogram.
6 ×1000 = 6000
So, there are 6000 grams in 6 kilograms.
Question 2.
9 kg = _______g
Answer:
9 kg = 9000g
Explanation:
There are 1000 grams in 1 kilogram.
9 ×1000 = 3000
So, there are 9000 grams in 9 kilograms.
Find the equivalent capacity
Question 3.
7 L =_________ mL
Answer:
7 l = 1000ml
Explanation:
There are 1000 milliliters in 1 liter.
7 ×1000= 7000
So, 7l is equal to 7000 milliliters of water.
Question 4.
10 L = ____ mL
Answer:
10l = 10000ml
Explanation:
There are 1000 milliliters in 1 liter.
10 ×1000= 10000
So, 10l has 10000 milliliters of water.
Apply and Grow: Practice
Find the equivalent mass.
Question 5.
8 kg = 8000 g
Answer:
There are 1000 grams in 1 kilogram.
8 ×1000 = 8000
So, there are 8000 grams in 8 kilograms.
Question 6.
7 kg = 7000g
Answer:
There are 1000 grams in 1 kilogram.
7×1000 = 7000
So, there are 7000 grams in 7 kilograms.
Question 7.
4 kg = 4000g
Answer:
There are 1000 grams in 1 kilogram.
4 ×1000 = 4000
So, there are 4000 grams in 4 kilograms.
Question 8.
67 kg = 67000 g
Answer:
There are 1000 grams in 1 kilogram.
67 ×1000 = 3000
So, there are 67000 grams in 67 kilograms.
Find the equivalent capacity.
Question 9.
9 L = _____ mL
Answer:
9 l = 9000 ml
Explanation:
one liter is equal to 1000ml
9 x 1000 =9000ml
Question 10.
3 L = _____ mL
Answer:
3 l = 3000ml
Explanation:
one liter is equal to 1000ml
3 x 1000 =3000ml.
Question 11.
23 L = ____ mL
Answer:
23l = 23000ml
explanation:
one liter is equal to 1000ml
23 x 1000= 23000ml
Question 12.
40 L = _____ mL
Answer:
40 l = 40000ml
explanation:
one liter is equal to 1000ml
40 x 1000= 40000ml
Question 13.
What is the mass of the bag of apples in grams?

Answer:
2000g
Explanation:
There are 1000 grams in 1 kilogram.
2 ×1000 = 2000
So, there are 2000 grams of apples in bag.
Question 14.
YOU BE THE TEACHER
Your friend says that 4 liters is greater than 4,500 milliliters. Is your friend correct? Explain.
Answer:
one liter is equal to 1000m
4 l = 4000ml
my friend is not correct4 liters is less than 4500ml.
Question 15.
Writing
Compare the relationship between kilograms and grams to the relationship between liters and milliliters.
Answer:
one kilogram is equal to 1000g
one liter is equal to 1000ml
kilograms and grams are used measure solids
liters and milliliters are used to measure liquids.
Think and Grow: Modeling Real Life
Example
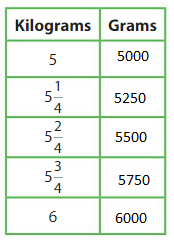
A restaurant chef has 5\(\frac{3}{4}\) kilograms of rice. A recipe uses 5,875 grams of rice. Does the chef have enough rice to follow the recipe?

Make a table that shows the relationship between kilograms and grams.
Compare 5\(\frac{3}{4}\) kilograms to 5,875 grams.
The chef _____ have enough rice to follow the recipe.
Answer:
No, The chef doesnot have enough rice to follow the recipe
Show and Grow
Question 16.
Your goal is to drink 1,500 milliliters of water each day. Yesterday, you drank 2\(\frac{1}{2}\) liters of water. Did you reach your goal?
Answer:
Goal=1500 ml
drank water = 2 x 1/2 =5/2= 2.5
2.5 x 1000 =2500ml
yes, I reached the goal.
Question 17.
Which egg has a greater mass? How much greater?

Answer:
ostrich egg
Explanation:
There are 1000 grams in 1 kilogram.
1 x 1/4 = 5/4 = 1.25kgs
but chicken egg is 581grams so ostrich egg is bigger
Question 18.
DIG DEEPER!
A scientist has 3 liters, 818 milliliters, and 410 milliliters of a solution in each of 3 beakers. The scientist wants to divide the solution equally among 7 beakers. How much of the solution should the scientist put into each beaker?
Answer:
In three beakers 1 has 3 liters, 2 has 818, 3 has 410.
he has to divide them to 7 beakers equally
3 x 1000 = 3000 + 818 + 410 = 4228
the total solution is 4228 ml is divided by 7 = 604
Mass and Capacity in Metric Units Homework & Practice 11.2
Find the equivalent mass.
Question 1.
2 kg = _________ g
Answer:
2 kg = 1000 g
Explanation:
There are 1000 grams in 1 kilogram.
2 ×1000 = 2000
So, there are 2000 grams in 2 kilograms.
Question 2.
10 kg = ________g
Answer:
10 kg = 10000 g
Explanation:
There are 1000 grams in 1 kilogram.
10×1000 = 10000
So, there are 10000 grams in 10 kilograms.
Question 3.
50 kg =_________g
Answer:
50 kg =50000g
Explanation:
There are 1000 grams in 1 kilogram.
50 ×1000 = 50000
So, there are 50000 grams in 50 kilograms.
Question 4.
31 kg = _________ g
Answer:
50 kg =50000g
Explanation:
There are 1000 grams in 1 kilogram.
51 ×1000 = 51000
So, there are 51000 grams in 51 kilograms.
Find the equivalent capacity.
Question 5.
7 L = _____ mL
Answer:
7l = 7000 ml
Explanation:
There are 1000 milliliters in 1 liter.
7 ×1000= 7000
So, 7l is equal to 7000 milliliters.
Question 6.
4 L = ____ mL
Answer:
4 l =4000 ml
Explanation:
There are 1000 milliliters in 1 liter.
4 ×1000= 4000
So, 4l has 4000 milliliters.
Question 7.
8 L = ____ mL
Answer:
8 l = 8000ml
Explanation:
There are 1000 milliliters in 1 liter.
8 ×1000= 8000
So, 8l has 8000 milliliters.
Question 8.
11 L = ____ mL
Answer:
11 l = 11000ml
Explanation:
There are 1000 milliliters in 1 liter.
11 ×1000= 11000
So, 8l has 11000 milliliters.
Question 9.
A pitcher contains 3 liters of iced tea. How many milliliters of iced tea does the pitcher contain?
Answer:
3000mm
Explanation:
There are 1000 milliliters in 1 liter.
3 ×1000= 3000
So, the container holds 3000 milliliters of iced tea the pitcher.
Question 10.
Number Sense
The prefix “kilo-” means one thousand. The prefix “milli-” means one-thousandth. How does the meaning of each prefix relate to the metric units of mass and capacity in this lesson?
Answer:
meter
Explanation:
The prefix “kilo-” means one thousand. The prefix “milli-” means one-thousandth. To measure the values of the meaning of each prefix relate to the metric units of mass and capacity in this lesson
Question 11.
Number Sense
When measuring the mass of a chair, how will the size of the unit affect the size of the measurement?
Answer:
Dimensions are physical qualities one relates the other in the size of measurement.
Question 12.
Modeling Real Life
To cook a pound of pasta, you need1toboil 4,700 milliliters of water. You fill a pot with 4\(\frac{1}{4}\) liters of water. Is there enough water in your pot?
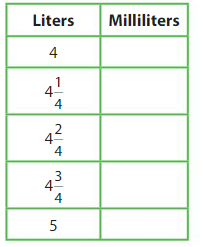
Answer:
not enough
Explanation:
To cook a pound of pasta, you need1toboil 4,700 milliliters of water. You fill a pot with 4250 is not enough.
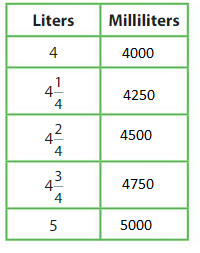
Question 13.
DIG DEEPER!
A 4,500-gram bag of soil costs $3, and an 18-kilogram bag of soil costs $10. Which is the less expensive way to buy 18,000 grams of soil? Explain.

Answer:
18kg bag
Explanation:
one kg is equal to 1000grams
18kg= 18000grams which costs of 10$
4500 g =3$
Review & Refresh
Find the difference. Then check your answer.
Question 14.
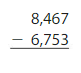
Answer: 1714
Question 15.
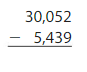
Answer: 24613
Question 16.
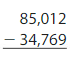
Answer: 50243
Lesson 11.3 Length in Customary Units
Explore and Grow
Work with a partner. Use a yardstick todraw3 lines on a whiteboard that are 1 yard,2 yards, and 3 yards in length. Then measure the lengths of the lines in feet and in inches. Think: How do the lengths, in inches, compare to the lengths in feet? How does each length compare to 1 yard?
1 foot is ____ times as long as 1 inch.
1 yard is _____ times as long as 1 foot.
1 yard is _____ times as long as 1 inch.
Answer:
1 foot is 12 times as long as 1 inch.
1 yard is 3 times as long as 1 foot.
1 yard is 36 times as long as 1 inch.
Structure
You know the length of an object in feet. Without measuring, how can you find its length in inches?
Answer:
consider the length of an object is x
if we that in inches we have to multiply with 12
so, the answer is 12x
Think and Grow: Find Equivalent Customary Lengths
Customary units of length include inches, feet, yards, and miles.

Example
Find the number of yards in 2 miles.
There are _____ yards in 1 mile.
2 × _____ = _____
So, there are _____ yards in 2 miles.
Answer:
There are 1760 yards in 1 mile.
2 × 1760 = 3250
So, there are 3520 yards in 2 miles.
Example
Find the number of inches in 7 yards.

There are _____ feet in 1 yard.
7 × _____ = _____ feet
There are ______ inches in 1 foot.
21 × ____ = ____ inches
So, there are ________ inches in 7 yards.
answer:
There are 3 feet in 1 yard.
7 × 3 = 21 feet
There are 12 inches in 1 foot.
21 × 12 = 252 inches
So, there are 252 inches in 7 yards.
Show and Grow
Find the equivalent length.
Question 1.
6 mi= _____ yd
Answer:
6 mi =10560yd
explanation:
Answer:
There are 1760 yards in 1 mile.
6 × 1760 =10560
So, there are 10560 yards in 6 miles.
Question 2.
4 ft = _____ in.
Answer:
4 ft = 48 in
Answer:
There are 12 inches in 1 feet.
12 × 4 = 48
So, there are 48 inches in 4 ft.
Question 3.
11 yd = _____ ft
Answer:
11yd = 33 ft.
Explanation:
one yard is equal to 3 feet
11x 3= 33ft
Question 4.
3 mi = _____ ft
Answer:
3 mi = 15840 ft
Explanation:
one mile is equal 5280 feet
3 x 5280 = 15840ft
Apply and Grow: Practice
Find the equivalent length.
Question 5.
10 ft = ______ in.
Answer:
10 ft = 120 in
Explanation:
one feet is equal to 12 inch
10 x 12= 120in
so, there are 120 in in 10 ft.
Question 6.
8 yd = ______ in.
Answer:
8 yards = 288 in.
Explanation:
one yard is equal to 36 inches
8 x 36 = 288in
Question 7.
2 mi = ______ ft
Answer:
2mi = 10560 ft
Explanation:
one mile is equal to 5280 ft
2 x 5280 = 10560.
Question 8.
9 mi = ______ yd
Answer:
9 mi = 15840yd
Explanation:
Answer:
There are 1760 yards in 1 mile.
9 × 1760 = 15840
So, there are 15840 yards in 9 miles.
Question 9.
4 yd = ______ in.
Answer:
4 yd = 144 in
Explanation:
one yard is equal to 36 inch
4 x 36 = 144in
Question 10.
20 ft = ______ in.
Answer:
20ft = 240 in
Explanation:
one ft is equal to 36 inch
20 x 36 = 240in
Question 11.
7 mi = ______ yd
Answer:
7 mi = 12320yd
Explanation:
Answer:
There are 1760 yards in 1 mile.
7 × 1760 = 12320
So, there are 12320 yards in 7 miles.
Question 12.
5 mi = ______ ft
Answer:
5mi = 26400 ft
Explanation:
one mile is equal to 5280 feet.
5 x 5280 = 26400 ft.
Question 13.
You ran 54 yards. How many feet did you run?
Answer:
one yard is equal to 3 feet
54 x 3=162 ft
I need to run 162 feet in 54 yards
Question 14.
Precision
Three students measure the height of a bookshelf. Student A measures 72 units, Student B measures 2 units, and Student C measures 6 units. The teacher says all three students are correct. What units did each student use?
Answer:
1 feet = 12 inch
1 yard = 3 feet
1 yard = 36 inch
student A measures in inch
student B measures in yards
student c measures in feet.
Question 15.
Reasoning
What is one way you can check whether an answer is reasonable when converting from larger units to smaller units?
Answer:
converting from yards to feet
Think and Grow: Modeling Real Life
Example
A football player needs to run 6\(\frac{1}{3}\) yards to score. The player runs 17 feet. Does the player score?
Make a table that shows the relationship between yards and feet.
Compare 6\(\frac{1}{2}\) yards to 17 feet.
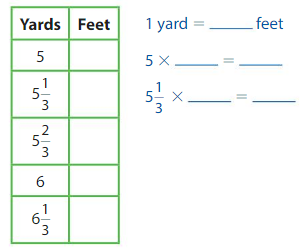
The player _____ score

Answer: 19
Show and Grow
Question 16.
You have 3\(\frac{1}{4}\) feet of string. You need 36 inches of string to make a necklace. Do you have enough string to make the necklace?
Answer: 9 inches
Question 17.
Which snake is longer? How much longer?

Answer: green anaconda
one yard is equal to 3 feet
green anaconda 28/3 = 9.33 x 3= 27.99feet
Question 18.
DIG DEEPER!
You have 6 yards of ribbon. You wrap 3 feet of ribbon around a present. You wrap 16 inches of ribbon around another present. How many inches of ribbon do you have left?
Answer:
one yard is equal to 3 feet
6 x 3 =18
I have 18 feet of ribbon in total
3 feet for gift wrapping
18-3= 15
one feet is equal to 12 inch
12 inch ribbon for the 2 nd present
15-12 =3
so, the remaining ribbon is 3 inch.
Length in Customary Units Homework & Practice 11.3
Find the equivalent length.
Question 1.
25 ft = _____ in.
Answer:
300 in
Explanation:
one feet is equal to 12 inch
25 x 12 = 300in
there are 300 inches in 25 feet.
Question 2.
3 mi = _____ yd
Answer:
3mi = 5280yd
Explanation:
There are 1760 yards in 1 mile.
3 × 1760 = 5280
So, there are 5280 yards in 3 miles.
Question 3.
7 yd = _____ ft
Answer:
21 feet
Explanation:
one yard is equal to 3 feet.
7 x 3 = 21ft
there are 21 feet in 7 yards.
Question 4.
9 yd = _____ in.
Answer:
324
Explanation:
one yard is equal to 36 inch
9 x 36=324.
so, there are 324 inch in 9 yards
Question 5.
5 mi = _____ yd
Answer:
5 mi =8800 yd
Explanation:
There are 1760 yards in 1 mile.
5 × 1760 = 8800
So, there are 8800 yards in 5 miles.
Question 6.
6 mi = _____ ft
Answer:
31680
Explanation:
one mile is equal to 5280 ft
6 x 5280 = 31680
so there are 5280 feet in 6 miles
Question 7.
\(\frac{1}{4}\)mi = _____ yd
Answer:
440yd
Explanation:
There are 1760 yards in 1 mile.
1760/4 = 440
So, there are 440 yards.
Question 8.
\(\frac{1}{3}\) yd = ____ ft
Answer:
1 feet
one yard is equal to 3 feet
1/3 x 3 = 1
Question 9.
A street is 2 miles long. How long is the street in yards?
Answer:
3520yd
Explanation:
There are 1760 yards in 1 mile.
2 × 1760 = 3250
So, there are 3520 yards in 2 miles.
Question 10.
Number Sense
Does it take more miles or more yards to equal a given length? Explain.
Answer:
when it is measured in miles 1 mile =1760 yd
as the miles contains less units it is easy to calculate.
Question 11.
YOU BE THE TEACHER
Your friend says 1 inch is \(\frac{1}{12}\) of a foot. Is your friend correct? Explain.
Answer:
he is correct
explanation:
one feet is equal to 12 inch
Question 12.
Number Sense
Which lengths are equivalent?

Answer:
15 yards = 45 feet, 540 inch
540 inch = 45 feet
Question 13.
Modeling Real Life
A plumber has 6\(\frac{1}{3}\) feet of piping. She needs inches of piping. Does she have enough piping?
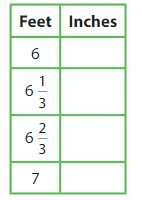
Answer:
A plumber has 6\(\frac{1}{3}\) feet of piping. she needs 38 inches of piping.
Question 14.
Modeling Real Life
A teacher has 12 yards of string for her class to make balloon zip lines. Each zipline needs 8 feet of string. How many zip lines can the class make?

Answer:
The teacher has 12 yards of string for her class to make balloon zip lines. Each zipline needs 8 feet of string
1 yard is equal to 3 feet
12 x 3 = 36
36/8 = 4
so they can make 4 zip lines of 8 feets each.
Review & Refresh
Divide. Then check your answer.
Question 15.
\(\sqrt [ 3 ]{ 501 } \)
Answer:
67.14
Question 16.
\(\sqrt [ 2 ]{ 4,237 } \)
Answer:
130.18
Question 17.
\(\sqrt [ 5 ]{ 6,049 } \)
Answer:
388.87
Lesson 11.4 Weight in Customary Units
Explore and Grow
Use a platform scale to help you complete the statement.
1 pound is ______ times as heavy as 1 ounce.

1 pound is 16 times as heavy as 1 ounce.
How can you use the number line to complete the statement?

1 ton is ________times as heavy as 1 pound.
Answer:
1 ton is 2240 times as heavy as 1 pound.
Structure
You know the weight of an object in pounds. Without measuring, how can you find its weight in ounces?
Answer:
one pound is equal to 16 times of a ounce by multiplying with the number.
Think and Grow: Find Equivalent Customary Weights
Customary units of weight include ounces, pounds, and tons.

Example
Find the number of ounces in 6 pounds.
There are ______ ounces in 1 pound.
6 × _____ = ____
So, there are _______ ounces in 6 pounds.
Answer:
There are 16 ounces in 1 pound.
6 × 16 = 96
So, there are 96 ounces in 6 pounds..
Example
The vehicle shown weighs 8 tons. What is the weight in pounds?

There are ______ pounds in 1 ton.
8 × _____ = _____
So, the vehicle weighs ______ pounds.
Answer:
There are 2000 pounds in 1 ton.
8 × 2000 = 16000
So, the vehicle weighs 16000 pounds.
Show and Grow
Find the equivalent weight.
Question 1.
5 T = ____ lb
Answer:
5 t = 10000 lb
Explanation:
There are 2000 pounds in 1 ton.
5 × 2000 = 10000
So, it weighs 10000 pounds.
Question 2.
9 lb = _____ oz
Answer:
9 lb = 144 oz
Explanation:
There are 16 ounces in 1 pound.
9 × 16 = 144
So, there are 144 ounces in 9 pounds..
Question 3.
15 lb = ____ oz
Answer:
15 lb = oz240
Explanation:
There are 16 ounces in 1 pound.
15 × 16 = 144
So, there are 240 ounces in 15 pounds..
Question 4.
7 T = _____ lb
Answer:
7 t = 14000 lb
Explanation:
There are 2000 pounds in 1 ton.
7 × 2000 = 14000
So, it weighs 14000 pounds.
Apply and Grow: Practice
Find the equivalent weight.
Question 5.
6 T = _____ lb
Answer:
6 t = 12000 lb
Explanation:
There are 2000 pounds in 1 ton.
6 × 2000 = 12000
So, it weighs 12000 pounds.
Question 6.
20 lb = ____ oz
Answer:
20 lb = oz
Explanation:
There are 16 ounces in 1 pound.
9 × 16 = 320
So, there are 320 ounces in 16 pounds..
Question 7.
12 lb = _____ oz
Answer:
12 lb = 192 oz
Explanation:
There are 16 ounces in 1 pound.
12 × 16 = 192
So, there are 192 ounces in 12 pounds..
Question 8.
2 T = _____ lb
Answer:
2 t = 4000 lb
Explanation:
There are 2000 pounds in 1 ton.
2 × 2000 = 4000
So, it weighs 4000 pounds.
Question 9.
4 T = ______ lb
Answer:
4 t = 8000 lb
Explanation:
There are 2000 pounds in 1 ton.
4 × 2000 = 8000
So, it weighs 8000 pounds.
Question 10.
11 lb = _____ oz
Answer:
11 lb = 176 oz
Explanation:
There are 16 ounces in 1 pound.
11 × 16 = 176
So, there are 176 ounces in 11 pounds..
Question 11.
15 lb = _____ oz
Answer:
15 lb = 240oz
Explanation:
There are 16 ounces in 1 pound.
15 × 16 = 240
So, there are 240 ounces in 15 pounds..
Question 12.
10 T = _____ lb
Answer:
10 t = 20000 lb
Explanation:
There are 2000 pounds in 1 ton.
10 × 2000 = 20000
So, it weighs 20000 pounds.
Question 13.
A bag of flour weighs 5 pounds. What is the weight of the bag of flour in ounces?
Answer:
5 lb = 80 oz
Explanation:
There are 16 ounces in 1 pound.
5 × 16 = 80
So, there are 80 ounces in 5 pounds.
Open-Ended Complete the statement.
Question 14.
54 ounces > _____ pounds
Answer: 54 ounces > 3.375
Question 15.
5,500 pounds < ______ tons
Answer:
5,500 pounds < 3 tons
DIG DEEPER!
Compare
Question 16.
![]()
Answer: 2 lb > 25 oz
Question 17.
![]()
Answer:6,500 < 7 t
Think and Grow: Modeling Real Life
Example
A river otter eats 64 ounces of food each day. A zookeeper has 3\(\frac{1}{2}\) pounds of fish to feed the otter. Does the zookeeper have enough food to feed the otter for 1 day?

Make a table that shows the relationship between pounds and ounces.
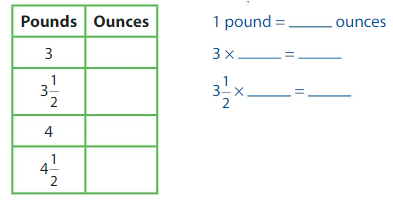
Compare 64 ounces to 3\(\frac{1}{2}\) pounds.
The zookeeper ______ have enough food to feed the otter for 1 day.
Answer:
A river otter eats 64 ounces of food each day. A zookeeper has 3\(\frac{1}{2}\) pounds of fish to feed the otter. The zookeeper does not have enough food to feed the otter for 1 day
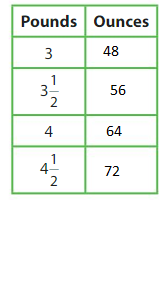
Show and Grow
Question 18.
The weight limit of a bridge is10,000 pounds. Can the van cross the bridge?

Answer:
4.25 t = 8500 lb
Explanation:
There are 2000 pounds in 1 ton.
4.25 × 2000 = 8500
So, it weighs 8500 pounds.
Question 19.
Your backpack weighs 3\(\frac{1}{2}\) pounds. You take a 4-ounce book out of your backpack. How many ounces does your backpack weigh now?
Answer:
3.5 lb x 16 = 56
Explanation:
There are 16 ounces in 1 pound.
3.5 × 16 = 56
So, there are 56 ounces in 3.5 pounds. The bag pack weighs 56-4 = 52 oz.
Question 20.
DIG DEEPER!
A 195-pound man has twenty-five 40-pound packages to deliver. Can he bring all of the packages on the elevator at once? Explain.

Answer:
2 t = 2000 lb
Explanation:
There are 2000 pounds in 1 ton.
25 x 40 = 1000
so he can easily take it once in the elevator.
Weight in Customary Units Homework & Practice 11.4
Find the equivalent weight.
Question 1.
3 T = _____ lb
Answer:
3 t = 6000 lb
Explanation:
There are 2000 pounds in 1 ton.
3 × 2000 = 6000
So, it weighs 6000 pounds.
Question 2.
13 lb = ____ oz
Answer:
13 lb = 208 oz
Explanation:
There are 16 ounces in 1 pound.
13 × 16 = 208
So, there are 208 ounces in 13 pounds.
Question 3.
22 lb = ____ oz
Answer:
22 lb = 352 oz
Explanation:
There are 16 ounces in 1 pound.
22 × 16 = 352
So, there are 352 ounces in 22 pounds.
Question 4.
8 T = _____ lb
Answer:
8 t = 16000 lb
Explanation:
There are 2000 pounds in 1 ton.
8 × 2000 = 16000
So, it weighs 16000 pounds.
Question 5.
2 T = ____ lb
Answer:
2 t = 4000 lb
Explanation:
There are 2000 pounds in 1 ton.
2 × 2000 = 4000
So, it weighs 4000 pounds.
Question 6.
20 lb = ______ oz
Answer:
20 lb = 320 oz
Explanation:
There are 16 ounces in 1 pound.
20 × 16 = 320
So, there are 320 ounces in 16 pounds.
Question 7.
5\(\frac{3}{4}\) lb = _____ oz
Answer:
5.75 lb = 93 oz
Explanation:
There are 16 ounces in 1 pound.
5.75 × 16 = 93
So, there are 93 ounces in 5.75 pounds.
Question 8.
6\(\frac{1}{4}\) T = _____ lb
Answer:
6.25 t = 12500 lb
Explanation:
There are 2000 pounds in 1 ton.
6.25 × 12500 = 10000
So, it weighs 12500 pounds.
Question 9.
A hippopotamus weighs 4 tons. What is the weight of the hippopotamus in pounds?

Answer:
4 t = 8000 lb
Explanation:
There are 2000 pounds in 1 ton.
4 × 2000 = 8000
So, hippo weighs 8000 pounds.
Question 10.
Writing
Explain how to compare tons to ounces.
Answer:
calculate to pounds and then to ounces
Question 11.
Modeling Real Life
Workers need 20,000 pounds of concrete to create a driveway. The boss orders 10\(\frac{3}{4}\) tons of concrete.Does he order enough?
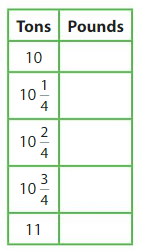
Answer:
43/4t = 21500 lb
Explanation:
There are 2000 pounds in 1 ton.
43/4 × 2000 = 21500
So, it weighs 21500 pounds yes he ordered enough concrete.
Question 12.
Modeling Real Life
You buy crushed tomatoes in 6-ounce cans. You want to1make a recipe that calls for 1\(\frac{1}{2}\) pounds of crushed tomatoes. How many cans do you need to make the recipe?
Answer:
6 ounce cans are there
1.5 pounds of crushed tomatoes
1.5 x 16= 24 ounce
one pound is equal to 16 ounce
we need 3 cans
Question 13.
DIG DEEPER!
How many more ounces does the heaviest puppy weigh than the lightest puppy?
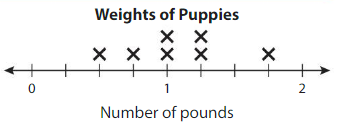
Answer: 3/4 is the lightest puppy
7/4 is the heaviest puppy
Review & Refresh
Find the sum
Question 14.
\(\frac{2}{8}+\frac{4}{8}\) = _______
Answer: 6
Question 15.
\(\frac{1}{2}+\frac{4}{2}\) = _______
Answer: 2.5
Question 16.
\(\frac{5}{12}+\frac{3}{12}+\frac{1}{12}\) = ______
Answer:
0.41+4+0.8
=5
Lesson 11.5 Capacity in Customary Units
Explore and Grow
Use the diagram to complete each statement. Then check your answers using a gallon measurement set.
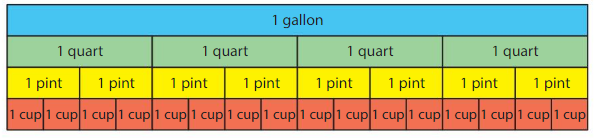
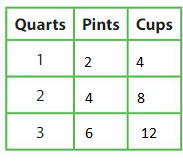
1 gallon is _____ times as much as 1 quart.
1 quart is _______ times as much as 1 pint.
1 pint is ______ times as much as 1 cup.
1 gallon is _____ times as much as 1 cup.
Answer:
1 gallon is 4 times as much as 1 quart.
1 quart is 2 times as much as 1 pint.
1 pint is 2 times as much as 1 cup.
1 gallon is 16 times as much as 1 cup.
Structure
You know the capacity of a container in pints. Without measuring, how can you find its capacity in cups?
Answer: multiplying with 2
Think and Grow: Find Equivalent Customary Capacities
Customary units of capacity include cups, pints, quarts, and gallons.

Example
Find the number of quarts in 15 gallons.
There are ______ quarts in 1 gallon.
15 × _____ = _____
So, there are ______ quarts in 15 gallons.
Answer:
There are 4 quarts in 1 gallon.
15 × 4 = 60
So, there are 60 quarts in 15 gallons.
Example
Find the number of cups in 7 quarts.

There are _____ pints in 1 quart.
7 × ____ = ____ pints
There are ______ cups in 1 pint.
14 × _____ = _____ cups
So, there are ______ cups in 7 quarts.
Answer:
There are 2 pints in 1 quart.
7 × 2 = 14 pints
There are 2 cups in 1 pint.
14 ×2 =28cups
So, there are 28 cups in 7 quarts.
Show and Grow
Find the equivalent capacity.
Question 1.
4 pt = _____ c
Answer:
4 pt = 8 c
Explanation:
There are 2 pints in one cup
4 x 2 = 8.
so, there are 8 cups in 4 pints
Question 2.
6 qt = _____ pt
Answer:
6 qt =24 pt
Explanation:
There are 2 pints in 1 quart.
6 × 2 = 12 pints
There are 2 cups in 1 pint.
12 ×2 =24cups
So, there are 24 cups in 6 quarts.
Question 3.
9 gal = ____ qt
Answer:
9 gal =36 qt
Explanation:
one gallon is equal to 4 quarts
9x 4 = 36 qt
Question 4.
12 gal = _____ pt
Answer:
12 qt =48 pt
Explanation:
There are 2 pints in 1 quart.
12 × 2 = 24 pints
There are 2 cups in 1 pint.
24 ×2 =48cups
So, there are 48 cups in 24 quarts.
Apply and Grow: Practice
Find the equivalent capacity.
Question 5.
30 qt = ____ pt
Answer:
30 qt =120 pt
Explanation:
There are 2 pints in 1 quart.
30 × 2 = 60 pints
There are 2 cups in 1 pint.
60 ×2 =120cups
So, there are 120cups in 30 quarts.
Question 6.
5 gal = ____ pt
Answer:
5 gal = 40 pt
Explanation:
one gallon is equal to 4 quarts
5 x 4 = 20 qt
one quart is equal to 2 pints
20 x 2 =40
Question 7.
9 qt = _____ c
Answer:
9 qt = 36 c
Explanation:
one quart is equal to 4 cups
9 x 4 = 36 cups
Question 8.
8 gal = _____ qt
Answer:
8 gal = 32 qt
Explanation:
one gal is equal to 4 quarts
8 x 4 = 32.
Question 9.
25 pt = _____ c
Answer:
25 pt = 50 c
Explanation:
There are 2 pints in one cup
25 x 2 = 50.
so, there are 50 cups in 25 pints
Question 10.
11 gal = _____ pt
Answer:
11 gal = 88 pt
Explanation:
one gallon is equal to 4 quarts
11 x 4 = 44
one quart is equal to 2 pints
44 x 2 = 88
so, there are 88 pints in 11 gal.
Question 11.
18 gal = ____ qt
Answer:
18 gal = 106 qt
Explanation:
one gal is equal to 4 quarts
18 x 4 =106
Question 12.
16 qt = _____ c
Answer:
one quart is equal to 4 cups
Question 13.
You have a 10-gallon fish tank. How many quarts of water does it take to fill your fish tank?
Answer: 10 x 4 = 40 qt
40 quarts of water takes to fill the fish tank.
Question 14.
DIG DEEPER!
Which measurements are greater than 5 gallons?

Answer: 10 gallons 92 cups
Think and Grow: Modeling Real Life
Example
A berry salad uses 6 pints of blackberries, 2 quarts of strawberries, and 7 cups of blueberries. Which fruit do you use the greatest amount of?

Make a table that shows the relationship between quarts, pints, and cups.
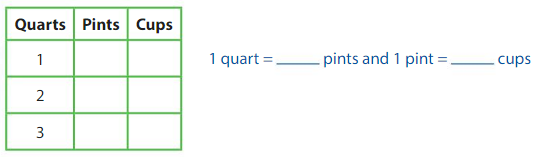
Compare 6 pints, 2 quarts, and 7 cups.
You use the greatest amount as quarts.
Show and Grow
Question 15.
A caterer buys 2 gallons of milk, 12 quarts of lemonade, and 32 pints of apple juice. Which drink does the caterer buy the least amount of?
Answer: pints
Question 16.
You make 4 quarts of soup. You and your friend each eat 1 pint of soup. Will the leftover soup fit into a 10-cup container? Explain.
Answer: 3 pints
Question 17.
DIG DEEPER!
You use 16 gallons of water while taking a shower. Your friend uses 288 cups. Who uses less water? How much less?
Answer: 16 x 4 = 64 quarts
64 x 2 = 128 pints
128 x 2 = 236
288 – 236 = 52.
Capacity in Customary Units Homework & Practice 11.5
Find the equivalent capacity.
Question 1.
7 pt = _____ c
Answer:
7 pt = 14 c
Explanation:
There are 2 pints in one cup
7 x 2 = 14.
so, there are 14 cups in 7 pints
Question 2.
10 qt = _____ pt
Answer:
10 qt =40 pt
Explanation:
There are 2 pints in 1 quart.
10 × 2 = 20 pints
There are 2 cups in 1 pint.
20 ×2 =40cups
So, there are 40 cups in 10 quarts.
Question 3.
8 gal = ______ qt
Answer:
8 x 4 = 36 qt
one gal is equal to 4 quarts.
Question 4.
4 gal = _____ pt
Answer:
4 gal = 36 pt
Question 5.
12 qt = _____ c
Answer:
1 qt = 2 cups
12 x 2 = 24 cups
Question 6.
6 gal = ______ qt
Answer:
6 gal = 28 qt
Explanation:
one gal is equal to 4 qt
6 x 4 = 28 qt
Question 17.
3\(\frac{1}{4}\) gal = _____ pt
Answer:
3.5 x 4 = 13
13 x 2 = 26
Question 8.
4 \(\frac{1}{2}\) pt = _____ c
Answer:
9/2 pt = 9 c
Explanation:
There are 2 pints in one cup
9/2 x 2 = 9.
so, there are 9 cups in 4.5 pints
Question 9.
A bottle holds \(\frac{1}{2}\) quart of liquid. How many cups of water does the bottle hold?
Answer:1 cups of water
Question 10.
Writing
Compare the relationship between pints and cups to the relationship between quarts and pints.
Answer:
1 pint = 2 cups
one quart = 2 pints
Question 11.
Logic
Your friend makes a table of equivalent capacities. What are the labels for the columns?
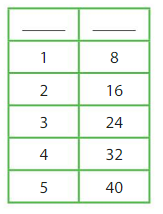
Answer: cups to quarts
Question 12.
Modeling Real Life
Turning off the faucet while brushing your teeth can conserve 32 quarts of water. Using a low-flow shower head can conserve15 gallons of water. Using a dishwasher can conserve112 pints of water. Which activity conserves the greatest amount of water?
Answer:
Explanation:
There are 2 pints in 1 quart.
52× 2 = 104 pints
Question 13.
Modeling Real Life
Some pitcher plants are large enough to hold 2 gallons of water. A household pitcher holds 16 cups of water. How much more water can a pitcher plant hold than the household pitcher?

Answer:
one gallon equal to 4 parts
2 x 4 = 8
8 quarts are needed.
Review & Refresh
Question 14.
A car dealership owner needs to transport 150 cars and 95 trucks to an island. A ferry can hold 8 vehicles. How many trips with vehicles will the ferry need to make?
Answer: 150 + 95 = 245
245/8 = 30. 8
it has to make almost 30 trips.
Lesson 11.6 Make and Interpret Line Plots
Explore and Grow
Measure your hand length with a ruler. Record the length to the nearest half-inch. Collect the hand lengths of all the students in your class, including yourself. Create a line plot of the results.
Think: How will you label the scale? What title will you give your line plot?

Construct Arguments
What conclusions can you make from the line plot?
Answer:
Teacher length is high when compared to kids
but the difference between the kids are less
Think and Grow: Make Line Plots
Example
You plant 10 seeds. After 6 days, you measure the height of each plant. Make a line plot to display the data.
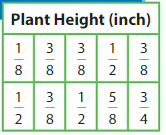
Step 1: Write the data values as fractions with the same denominator.
The denominators of the data values are 2, 4, and 8. Because 2 and 4 are factors of 8, use a denominator of 8.

Step 2: Use a scale on a number line that shows all of the data values.
Step 3: Mark an X for each data value.
Answer: 3/8
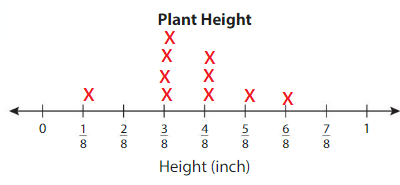
3/8 plant height is most common.
Show and Grow
Question 1.
You survey 10 people about the amount of water each person drinks in 1 day. Make a line plot to display the data.

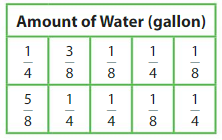
Which amount of water consumed is the most common?
Answer:
2/8

Explanation:
to make this make the denominator to equal
Apply and Grow: Practice
Question 2.
The table shows the lengths of 10 chameleons in a pet store. Make a line plot to display the data.
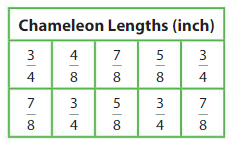
Which is most common chameleon length?
Answer:
6/8
Question 3.
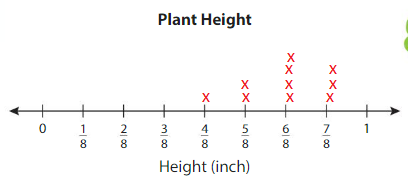
A scientist is studying the weights of 15 sugar gliders. Make a line plot to display the data.
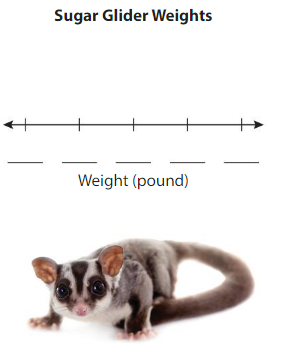
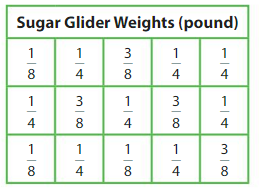
How many sugar gliders weigh more than \(\frac{1}{8}\) pound?
Answer:
Question 4.
DIG DEEPER!
Use your line plot from Exercise 3. How many times as many \(\frac{2}{3}\) pound sugar gliders are there as \(\frac{3}{8}[/latex] pound sugar gliders? Explain.
Answer:
2/8
Explanation:
denominator is equalized and the factors are multiplied.
Think and Grow: Modeling Real Life
Example
You record the distances you rode your bike for 10 days. What is the difference in the length of your longest ride and the length of your shortest ride?
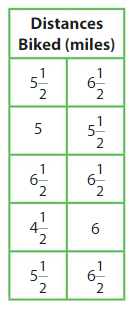
Make a line plot. Use a scale that shows all of the data values.
Subtract the shortest ride from the longest ride.
5 − 6 = 1.
The difference in the length of your longest ride and the length of your shortest ride is 1 miles.
Show and Grow
Question 5.
You record the total monthly rainfall for 10 months. What is the difference of the greatest monthly rainfall and the least monthly rainfall?
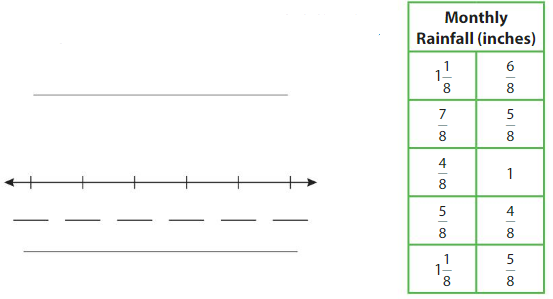
How much did it rain during the 10 months in all?
Answer:
the total rain fall during all the 10 months is 62/8
Make and Interpret Line Plots Homework & Practice 11.6
Question 1.
The table shows the thicknesses of 10 books in a series. Make a line plot to display the data.
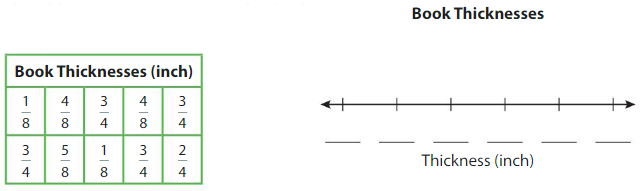
The least common thickness is ______ inch.
There are ______ books that are less than [latex]\frac{5}{8}\) inch thick.
Answer:

The least common thickness is 6/8 inch.
There are 4 books that are less than \(\frac{5}{8}\) inch thick.
Question 2.
DIG DEEPER!
Use your line plot from Exercise 1. How many times as many \(\frac{3}{4}\) inch thick books are there as \(\frac{1}{8}\)-inch thick books?

Answer:
6/8 are more

Question 3.
A zoologist is studying the weights of 15 skinks. Make a line plot to display the data.
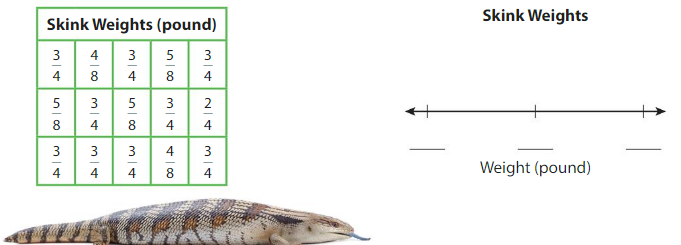
Answer:

Question 4.
Reasoning
In Exercise 3, do most of the skinks weigh more than \(\frac{5}{8}\) pound?
Answer:
yes most of the skinks weigh more than \(\frac{5}{8}\) pound.
Question 5.
Modeling Real Life
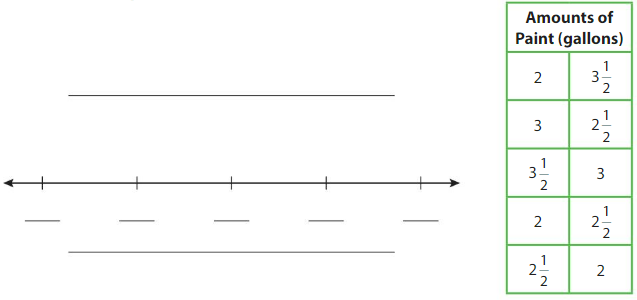
A painter records the amounts of paint he uses in 10 different rooms. What is the difference of the greatest amount of paint used and the least amount of paint used?
How many gallons of paint were used in all 10 rooms combined?
Answer:
4/2 is least paint used
7/2 is the greatest paint used
Review & Refresh
Write the fraction as a sum of unit fractions.
Question 6.
\(\frac{5}{6}\)
Answer:
0.83
Question 7.
\(\frac{8}{3}\)
Answer:
2.6
Lesson 11.7 Units of Time
Explore and Grow
Use a clock or a stopwatch to help you complete the statements.

1 minute is ______ times as long as 1 second.
1 hour is _______ times as long as 1 minute.
Answer:
1 minute is 60 times as long as 1 second.
1 hour is 60 times as long as 1 minute.
Structure
You know an amount of time in minutes. Without using a clock or a stopwatch, how can you find the amount of time in seconds?
Answer: multiply with 60.
Think and Grow: Find Equivalent Amounts of Time
Units of time include seconds, minutes, hours, days, weeks, months, and years.

Example
Find the number of minutes in 6 hours.
There are ______ minutes in 1 hour.
6 × _____ = _____
So, there are _____ minutes in 6 hours.
answer:
There are 60 minutes in 1 hour.
6 × 60 =120_
So, there are 120 minutes in 6 hours.
Example
Find the number of hours in 4 weeks.

There are ______ days in 1 week.
4 × _____ = ____ days
There are ______ hours in 1 day.
28 × _____ = ______
So, there are ____ hours in 4 weeks.
Answer:
There are 7 days in 1 week.
4 × 7 = 28 days
There are 24 hours in 1 day.
28 × 24 = 672
So, there are 672 hours in 4 weeks.
Show and Grow
Find the equivalent amount of time.
Question 1.
10 min = ______ sec
Answer:
one minute is equal to 60 seconds
10 x 60 = 600 seconds
Question 2.
5 d = _____ h
Answer:
5d = 120 h
Explanation:
one day is equal to 24 hours
5 x 24 = 120 h.
Question 3.
8 wk = _____ d
Answer:
8 wk = 56 days
Explanation:
one week is equal to 7 days
8 x 7 = 56 days
Question 4.
2 d = _____ sec
Answer:
2 d = sec
Explanation:
one day is equal to 24 hours
one hour is equal to 60 seconds
24 x 60 = 2880 sec
Apply and Grow: Practice
Find the equivalent amount of time.
Question 5.
7 yr = ____ wk
Answer:
7yr = 364 wk
Explanation:
one year is equal to 56 weeks
7 x 52 = 364 wk
q6.
4 d = _____ min
Answer:
4 d = 240 min
Explanation:
one day is equal to 60 minutes
4 x 60 = 240 min
Question 7.
3 wk = _____ d
Answer:
3 wk = 21 d
Explanation:
one week is equal to 7 days
3 x 7 = 21 days
Question 8.
6 h = _____ sec
Answer:
6 h = 360 sec
Explanation:
one hour is equal to 60 sec
6 x 60 = 360 sec
Question 9.
2 yr = _____ mo
Answer:
2 yr = 24 months
Explanation:
one year is equal to 12 months
2 x 12 = 24 months
Question 10.
1 wk = _____ h
Answer:
1 wk = 168 hours
Explanation:
one week is equal to 7 days
one day is equal to 24 hours
7 x 24 = 168 hours
Question 11.
24 h = _____ min
Answer:
24 h = 1440 min
Explanation:
one hour is equal to 60 minutes
24 x 60 = 1440 min
Question 12.
10 yr = _____ d
Answer:
10 yr = 3650 d
Explanation:
one year is equal 365 days
365 x 10 = 3650 days
Question 13.
Your friend turns 8 years old today. How many months old is your friend?
Answer:
8 y = 96 months
Explanation:
one year is equal to 12 months
8 x 12 = 96 months
my friend is 96 months old
Question 14.
Writing
Explain how you can show that 3,000 seconds is less than 1 hour.
Answer:
one min is equal to 60 sec
one hour is equal to 60 minutes
60 x 60 = 3600
3600- 3000 = 600 sec
one hour is equal to 3600 minutes
600 sec lesser.
Question 15.
Structure
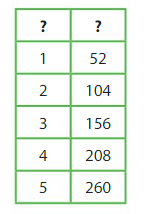
The number pairs describe the relationship between which two units of time? Explain.
2 and 104
3 and 156
4 and 208
Answer:
2 years is equal to 104 weeks
3 years is equal to 156 weeks
4 years is equal to 208 weeks
year and week relation ship
Think and Grow: Modeling Real Life
Example
Your cousin makes a 3\(\frac{1}{2}\) minute long music video. Your friend makes a 200-second long music video. Who records a longer music video?
Make a table that shows the relationship between minutes and seconds.
Compare 3\(\frac{1}{2}\) minutes to 200 seconds.
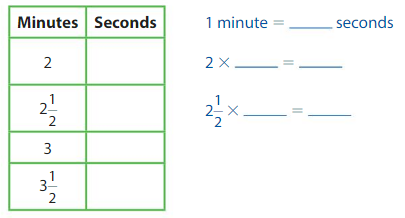
Your friend records a longer music video.
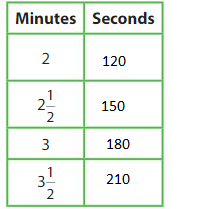
Show and Grow
Question 16.
You put a puzzle together in 150 minutes. Your friend puts the same puzzle together in 1hours. Who put the puzzle 2\(\frac{1}{4}\) together faster?
Answer:
one hour is equal to 60 min
You put a puzzle together in 150 minutes
2 x 1/ 4 = 2.25 x 60
= 135 min
Question 17.
In the wild, a California sea lion can live to be 20 years old. In captivity, it can live to be 360 months old. Does a California sea lion live longer in the wild or in captivity? How much longer?

Answer:
one year is equal to 12 months
20 x 12 = 240 months
360 is higher than 240 so in captivity.
Question 18.
Movie A is 98 minutes long. Movie B is 1\(\frac{1}{2}\) hours long. Movie C is 1\(\frac{3}{4}\) hours long. Order the movies from longest to shortest.
Answer:
movie a = 98 min
movie b = 90 min
movie c = 105 min
movies c is longest
Units of Time Homework & Practice 11.7
Find the equivalent amount of time.
Question 1.
9 yr = _____ wk
Answer:
9 yr = 468 wk
Explanation:
one year is equal to 52 week
9 x 52= 468 wk
Question 2.
10 min = _____ sec
Answer:
10 min = 600 sec
Explanation:
one minute is equal to 60 sec
10 x 60 =600 sec
Question 3.
1 wk = _____ h
Answer:
1 wk = 168 hours
Explanation:
one week is equal to 7 days
7 x 24 = 168 hours.
Question 4.
6 yr = _____ mo
Answer:
6 yr = months
Explanation:
one year is equal to 12 months
6 x 12 = 72 months
Question 5.
3 yr = _____ d
Answer:
3 yr = 1095 d
Explanation:
one year is equal to 365 days
3 x 365 = 1095 days
Question 6.
2 d = ______ min
Answer:
2 d =
Explanation:
one day is equal to 24 hours
one hour is equal to 60 min
2 x 24 = 48 hours
48 x 60 = 2880 min
Question 7.
\(\frac{1}{3}\) d = _____ h
Answer:
8 hours
Question 8.
2\(\frac{3}{4}\) yr = ______ wk
Answer:
2. 75 yr
one year is equal 52 week
2. 75 = 143 week
Question 9.
How many hours are in 1 week?
Answer:
one week is equal to 7 days
one day is equal to 24 hours
7 x 24 = 168 hours
Question 10.
YOU BE THE TEACHER
Your friend labels the first column Weeks and the second column Years. Is your friend correct? Explain.
Answer:
yes , my friend is correct the table discribes years and weeks.
Question 11.
DIG DEEPER!
How many days is Newton thinking of?

Answer:
one week is equal to 7 days
one day is equal to 24 hours
7 x 2 = 14
14 x 24 = 336 hours
yes newton is correct.
Question 12.
Modeling Real Life
You have 1\(\frac{1}{2}\) hours before dinner. You want to watch a movie that is 118 minutes long. Do you have enough time to watch the entire movie?
Answer: no
Question 13
DIG DEEPER!
The world record for holding a person vertically overhead with one hand is 1\(\frac{1}{12}\) minutes. The world record for holding a person horizontally overhead with one hand is 76 seconds. Which world record is longer? How much longer?
Answer:
one minute is equal to 60 sec
13/ 12 = 1.08
1. 08 x 60 = 65 sec
The world record for holding a person horizontally overhead with one hand is 76 seconds.
is longer
Review & Refresh
Find the product. Check whether your answer is reasonable.
Question 14.
Estimate: _____
418 × 3 = _____
Answer:
1254
Question 15.
Estimate: _____
729 × 5 = _____
Answer:
3645
Question 16.
Estimate: _____
9 × 3,026 = _____
Answer:
27234
Lesson 11.8 Problem Solving: Elapsed Time
Explore and Grow
Use a clock to help answer each question.
How much time has passed since you woke up?

How much time has passed since school started?
Answer:
If my school started at 9 o’ clock and now it is 3 o’ clock then the time passed is 6 hours
Construct Arguments
Explain to a partner how you found your answers.
Answer:
The time which had passed away we have to calculate that.
Think and Grow: Problem Solving: Time Intervals
Example
A dinosaur museum closes in 1\(\frac{1}{2}\) hours. Do you have enough time to spend 20 minutes at each of 4 exhibits in the museum?
Understand the Problem
What do you know?
• The museum closes in 1\(\frac{1}{2}\) hours.
• You want to spend 20 minutes at at each of 4 exhibits.
What do you need to find?
• You need to find whether you have enough time to spend 20 minutes at the each of 4 exhibits.museum closes.
Answers:
a. 1 x 1/2 = 3/ 2
1.5
one hour is equal to 60 min
1.5 x 60 = 90 min
b. there are 4 exhibits each takes 20 min
4 x 20 = 80 mins
90 – 80 = 10
c. so the time is sufficient
Make a Plan
How will you solve?
• Find the number of minutes until the museum closes.
• Find the total number of minutes it takes to visit the exhibits.
Solve
Step 1: Find the number of minutes until the museum closes.
There are ______ minutes in 1 hour.
1\(\frac{1}{2}\) × ____ = ______
There are _____ minutes until the museum closes.
Step 2: Find how many minutes it takes to visit the exhibits.
It takes _____ minutes to visit the exhibits, which is ______ than 90 minutes.
You ______ have enough time to visit the exhibits.
Show and Grow
Question 1.
You have a total of 9\(\frac{1}{2}\) minutes to complete 4 tasks in a video game. Do you have enough time to spend 150 seconds on each task?
Answer:
total time is 9 x1/2
19 / 2
= 9.5 min
9.5 x 60 = 570 sec
there are 570 sec in total
we have 4 tasks 150 s each
4 x 150= 600
600 – 570 = 30
we want more thirty sec to finish the task.
Apply and Grow: Practice
Understand the problem. What do you know? What do you need to find? Explain.
Question 2.
You spend 1\(\frac{1}{4}\) hours exploring the woods. Then you spend 25 minutes sitting at a campfire. How many total minutes do you spend exploring the woods and sitting at the campfire?
Answer:
my spend time is 1 x 1/4 = 5/4
=1.25
one hour is equal to 60 minutes 25 minutes sitting at a campfire.
1.25 x 60 = 75
Total minutes do me spend exploring the woods and sitting at the campfire is 75 minutes
Question 3.
A bodybuilder spends 2\(\frac{1}{2}\) hours lifting weights. She spends 20 minutes running. How many more minutes does she spend lifting weights than running?

Answer:
lifting weights is 2 x 1/2
3/2 = 1.5
1.5 x 60 = 90 min
running = 20
90 – 20= 70
she spend lifting weighs than running is 70 minutes.
Understand the problem. Then make a plan. How will you solve? Explain.
Question 4.
You visit an animal shelter for 1\(\frac{3}{4}\) hours. You spend an equal amount of time with each of the 7 animals. How many minutes do you spend with each animal?
Answer:
The animal shelter visiting time is 1 x 3/4 =
7 / 4 = 1.75
one hour is equal to 60 minutes
1.75 x 60= 105 minutes
an equal amount of time with each of the 7 animals
105 / 7
= 15minutes is the time me spend with each animal
Question 5.
A skate park closes in 3\(\frac{1}{4}\) hours. Do you have enough time to spend 15 minutes practicing each of 13 different skateboard tricks?
Answer:
A skate park closes at 13/4
3.25
one hour is equal to 60 minutes
3.25 x 60 = 195 min
15 x 13 =195
yes I have enough time to spend 15 minutes practicing each of 13 different skateboard tricks.
Question 6.
A basketball team practices drills for 20 minutes and then scrimmages for 40 minutes. The overall practice time is divided evenly into3 sessions. How many minutes is each session?
Answer:
drills = 20 min
scrimmages= 40 mins
drills + scrimmages
20 + 40 =60min
the total time is 60 min
it is divided to 3 equal parts that is 60/ 3 = 20 mins
Question 7.
A high school music concert is 55 minutes long. The band plays25 minutes to start the concert. The rest of the concert time is divided equally among the choir, band, orchestra, and jazz ensemble. For how many minutes does the orchestra play?
Answer:
Total time is 55 mins
25 mins to start the the concert
55-25= 30
there are 4 types
choir, band, orchestra, and jazz ensemble
orchestra plays 7.5 mins long
Think and Grow: Modeling Real Life
Example
Field day starts at 12:15 .. and ends at 3:30 ..You spend an equal amount of time at each activity.How much time do you spend at each activity?

Think: What do you know? What do you need to find? How will you solve?
Step 1: How long is field day?

Step 2: How many minutes long is field day?
There are ______ minutes in 1 hour. _____ × _____ = _____
____ + 15 = ______ Add 15 minutes.
Field day is ______ minutes long.
Step 3: Divide the total amount of time by the number of field day activities.
You spend _____ minutes at each activity.
Answer:
The field day is 3 hours 15 mins long
There are 60 minutes in 1 hour. 60 × 60 x 60 = 180
180+ 15 = Add 15 minutes.
Field day is 195 minutes long.
Divided the total amount of time by the number of field day activities.
Show and Grow
Question 8.
You start exercising at 6:30 A.M. and finish at 7:45 A.M. You spend an equal amount of time stretching, walking, and running. How much time do you spend doing each exercise?
Answer:
The total exercise time is 6:30 – 7.45 = 1hr 15 min
1 hr = 60 min
60 + 15 = 75/3 = 25 mins
time do you spend doing each exercise is 25 mins
Problem Solving: Elapsed Time Homework & Practice 11.8
Understand the problem. Then make a plan. How will you solve? Explain.
Question 1.
It takes Descartes 1\(\frac{1}{4}\) minutes to run 3 laps around his house. Each lap takes him the same amount of time. How many seconds does it take him to run each lap?

Answer:
5/4 = 1.25 x 60 = 75sec
one minute is equal to 60 sec
Each lap takes him the same amount of time 75 seconds it take him to run each lap.
Question 2.
You watch television for 60 minutes. There are 18 minutes of commercials. The rest of the time is divided evenly between 2 shows. How many minutes long is each show?
Answer:
Total watching time is 60m
18 mins for commercial 60 – 18 = 42
The rest of the time is divided evenly between 2 shows 42/2 = 24 minutes long is each show.
Question 3.
You spend 5\(\frac{1}{2}\) hours at the park this week. You spend 210 fewer minutes at the library than you do at the park. How many minutes do you spend at the library?
Answer:
hours at the park this week is 11/2 = 5.5
5.5 x 60 = 330
330 – 210 = 120 minutes.
Question 4.
Your class spends \(\frac{1}{4}\) hour setting up an experiment. You spend 55 more minutes recording data than you do setting up the experiment. For how many minutes do you record data?
Answer:
1/4 of hour is 60/4 =15min
You spend 55 more minutes recording data than you do setting up the experiment.
55-15 = 40 minutes you record data.
Question 5.
You have 7\(\frac{1}{2}\) minutes left to successfully complete 3 rock climbing walls. It normally takes 155 seconds to climb each wall. Do you have enough time to climb all three walls?

Answer:
15/2 = 7.5
=450 one min is equal to 60 sec
It normally takes 155 seconds to climb each wall 155 x 3 = 465
time to climb all three walls 465 – 450 = 15 sec less time.
The time does not enough to climb all the three walls
Question 6.
Writing
Write and solve a two-step word problem involving elapsed time.
Answer :
Sam and his mom arrive at the doctor’s office at 2:30 p.m. They see the doctor at 3:10 p.m. How long was their wait?
40 mins
Question 7.
Modeling Real Life
A family attends a family expo from 1:30 P.M. to 5:15 P.M. They spend an equal amount of time at each activity. How many minutes do they spend at each activity?

Answer:
There are 5 family expo activities timing from 1:30 to 5:30 is 4 hours
4 x 60 = 240 min
240/5 = 48 min they spend an equal amount of time at each activity.
Review & Refresh
Find the product.
Question 8.
20 × 50
Answer:
100
Question 9.
38 × 30
Answer:
1140
Question 10.
60 × 82
Answer:
4920
Lesson 11.9 Mixed Measures
Explore and Grow
Measure your height, the height of a classmate, and the height of your teacher. Write each height in the table.
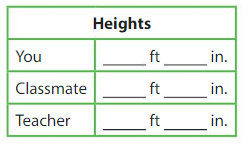
Who is taller, you or your classmate? How much taller?
Who is taller, you or your teacher? How much taller?
Answer:

Structure
Without measuring, how can you find each height in inches?
Answer:
by multiplying with 12
Think and Grow: Adding and Subtracting Mixed Measures
Example
Add 3 feet 4 inches and 2 feet 5 inches.

The differences is ____ hours ____ minutes
Answer:
The differences is 2 hours 48 minutes
Show and Grow
Add or Subtract
Question 1.
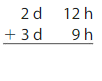
Answer:
5 days 21 hours
Question 2.

Answer:
3 T 1500 lb
Question 3.

Answer:
2 gal 14 c
Apply and Grow: Practice
Add or Subtract
Question 4.
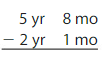
Answer:
3 yr 7 mon
Question 5.

Answer:
8 lb 11 oz
Question 6.
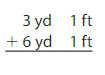
Answer:
9 yd 2 ft
Question 7.

Answer:
12 gal 3 qt
Question 8.
Answer:
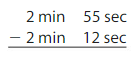
43 sec
Question 9.

Answer:
16 mi 591 yd
Question 10.
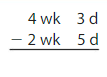
Answer:
1 wk 5 d
Question 11.
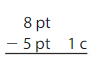
Answer:
2 pt 1 c
Question 12.
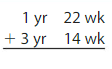
Answer:
4 yr 36 wk
Question 13.
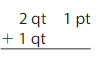
Answer:
3 qt 1 pt
Question 14.

Answer:
3 mi 4851ft
Question 15.

Answer:
12 gal 9 pt
Question 16.
A truck driver transports new vehicles. The total weight of the cargo is 14 tons 1,544 pounds. The truck driver drops off 1 car that weighs 1 ton1,693 pounds. What is the weight of the cargo now?

Answer:
12 ton 1851 pounds
Question 17.
DIG DEEPER!
Find the unknown numbers.

Answer:
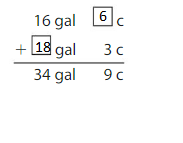
Question 18.
YOU BE THE TEACHER
Newton finds the difference between 5 yards 1 foot and 2 yards 2 feet. Is Newton correct? Explain.
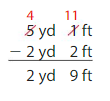
Think and Grow: Modeling Real Life
A commercial airplane is 121 feet 6 inches shorter than Air Force One. How long is the commercial airplane?

Subtract 121 feet 6 inches from the length of Air Force One.
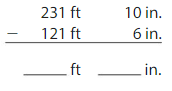
The commercial airplane is ______ feet ______ inches long.
Answer:
The commercial airplane is 110 feet 4 inches long.
Show and Grow
Question 19.
An art teacher has 3 quarts 1 pint of yellow paint. The teacher has 1 quart 2 pints less red paint than yellow paint. How much red paint does the teacher have?
Answer: 1 quart 3 pints
Question 20.
A 1-month-old puppy weighs 7 pounds 3 ounces. How much does the puppy weigh after 3 months?
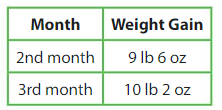
Answer:
10 lb 2 oz
Question 21.
DIG DEEPER!
How long do you work on your science fair project in all?

Answer: each part is raising by hundred
Mixed Measures Homework & Practice 11.9
Add or Subtract
Question 1.
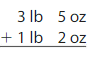
Answer:
4 lb 7 oz
Question 2.

Answer:
2 min 5 sec
Question 3.

Answer:
3 mi 825 ft
Question 4.

Answer:
1 t
Question 5.

Answer:
6 gal 2 qt
Question 6.

Answer:
5 hr 47 min
Question 7.
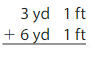
ans:
9 yd 2 ft
Question 8.

Answer:
6 pt
Question 9.
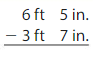
Answer:
2 ft 10 in
Question 10.
You are making punch. You use 3 quarts 1 pint of pineapple juice and 2 quarts 1 pint of orange juice.How much juice do you use?
Answer:
5 quart 2 pints
Question 11.
Writing
Explain when you need to regroup when subtracting mixed measures.
Answer:
To find out the lengths
Question 12.
Modeling Real Life
How much longer did it take one person to cycle the length of South America than a two-person team?
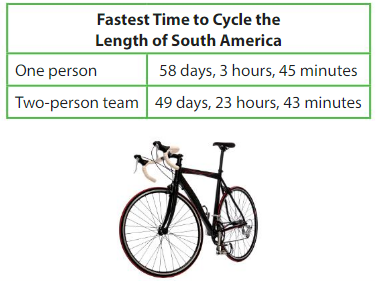
Answer:
8 days 4 hours 2 minutes
Question 13.
DIG DEEPER!
It rains 1 inch each day for 3 days. A meteorologist says that if the rain had been snow,each inch of rain would have been 1 foot 1 inch of snow. What would have been the total snowfall for the 3 days?

Answer:
3 foot 3 inch
Review & Refresh
Subtract
Question 14.
\(\frac{5}{10}-\frac{1}{10}\) = ______
Answer:
0.5 -0.1
= 0.4
Question 15.
\(\frac{9}{5}-\frac{4}{5}\) = ______
Answer:
1.8-0.8=
1
Question 16.
\(\frac{11}{12}-\frac{7}{12}\) = _____
Answer:
0.91-0.58=
0.33
Understand Measurement Equivalence Performance Task
You and a friend make a gravity-powered racer for an upcoming race.

Question 1.
The rules state that the racer must be less than 40 inches wide and less than 96 inches long. The weight of the racer must be less than 70 pounds.
a. Your racer is 2 feet wide and 1 yardlong. Does your racer meet the size requirements? Explain.
b. Your racer weighs 65 pounds without wheels, and each wheel weighs 22 ounces. Is your racer under the weight limit? Explain.
Answer:
a) one feet is equal to 12 inch
2 x 12 = 24
the required measurement is 40 inch
the racer does not met the requirments.
b) one pound equal to 16 ounce
so the racer original weight is 64 pounds 4 ounce
the required weight is 70 pounds /
so he is qualified
Question 2.
You test your racer on a track. The length of the track is \(\frac{1}{2}\) mile. What is the length of the track in feet?
Answer:
one mile is equal 5280 feet
5280/ 2 = 2640 feet
the track length is 2640
Question 3.
The table shows the race times for all of the teams.
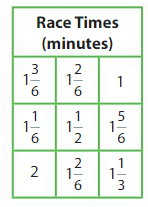
a. Make a line plot to display the data.
b. How many seconds later did the last team finish than the first team?
Answer: after one minute
Question 4.
After the race, you drink 5 cups of water and your friend drinks 3 pints of water. Who drinks more water? How much more?
Answer:
my friend drank the more water
one pint is equal to 2 cups
3 x 2 = 6
I drank 5 cups my friend drink 6 cups
Understand Measurement Equivalence Activity
Conversion Flip and Find
Directions:
1. Choose which conversion cards you will play with.
2. Place the cards face down on the board.
3. Players take turns flipping two cards.
4. If your two cards show equivalent measures, keep the cards. If your cards show different measures, flip the cards back over.
5. The player with the most matches wins!

Understand Measurement Equivalence Chapter Practice
11.1 Length in Metric Units
Find the equivalent length.
Question 1.
7 km = _____ m
Answer:
7 km = 7000m
Explanation:
one kilometer is equal to 1000m
7 x 1000= 7000m
so there are 7000 meter in 7 km
Question 2.
9 m = _____ mm
Answer:
9 m = 9000mm
Explanation:
one meter is equal to 1000 millimeter
9 x 1000 = 9000
so there are 9000 mm in 9 m.
Question 3.
3 cm = _____ mm
Answer:
3 cm = 30 mm
Explanation:
one cm is equal to 10 mm
3 x 10 = 30mm
so there are 30mm in 3 cm
Question 4.
5 km = _____ cm
Answer:
5 km = 500000 cm
Explanation:
one kilometer is equal to 1000 m
5 x 1000 = 5000m
one meter is equal to 100 cm
5000 x 100 = 500000cm.
11.2 Mass and Capacity in Metric Units
Find the equivalent mass.
Question 5.
3 kg = _____ g
Answer:
3 kg = 3000g
Explanation:
one kg is equal to 1000 g
3 x 1000 = 3000g
so there are 3000g in 3 kg.
Question 6.
7 kg = _____ g
Answer:
7 kg = 7000g
Explanation:
one kg is equal to 1000g
7 x 1000 = 7000g
so there are 7000 g in 7 kg
Question 7.
8 kg = _____ g
Answer:
8 kg = 8000g
Explanation:
one kg is equal to 1000 grams
8 x 1000 = 8000g
so there are 8000g in 8 kg
Question 8.
46 kg = ____ g
Answer:
46 kg = 46000g
Explanation:
one kg is equal to 1000 g
46 x 1000= 46000g
so there are 46000 g in 46kgs
Find the equivalent capacity.
Question 9.
2 L = _____ mL
Answer:
2 L = 2000ml
Explanation:
one liter is equal to 1000ml
2 x 1000 = 2000l
so there are 2000 ml in 2L
Question 10.
10 L = _____ mL
Answer:
10 L = 10000ml
Explanation:
one liter is equal to 1000ml
10 x 1000 = 10000l
so there are 10000 ml in 10L
Question 11.
4 L = ____ mL
Answer:
4 L = 4000ml
Explanation:
one liter is equal to 1000ml
4 x 1000 = 4000l
so there are 4000 ml in 4L
Question 12.
98 L = ____ mL
Answer:
98 L = 98000ml
Explanation:
one liter is equal to 1000ml
98 x 1000 = 98000l
so there are 98000 ml in 98L
Question 13.
What is the mass of the potatoes in grams?

Answer:
5 kg = 5000g
Explanation:
one 1 kg is equal to 1000g
5 x 1000 g = 5000g
11.3 Length in Customary Units
Find the equivalent length.
Question 14.
8 ft = ___ in.
Answer:
one feet is equal to 12 inch
8 x 12 = 96inch
Question 15.
10 yd = _____ ft
Answer:
10 yd = 30 ft
Explanation:
one yard is equal to 3 feet
10 x 3 = 30 feet
Question 16.
12 yd = _____ in.
Answer:
12 yd = 432 in.
Explanation:
one yard is equal to 3 feet
12 x 3 =36 feet
one feet is equal to 12 inch
36 x 12 = 432inch.
Question 17.
\(\frac{3}{4}\) mi = _____ yd
Answer:
one mile is equal to 1760 yard
3/ 4 of 1760 is 1320
Question 18.
Modeling Real Life
You have a 4-foot-long roll of magnetic tape. You use 2 inches for each picture you hang on the refrigerator. How many pictures can you hang?

Answer:
I have 4 foot of magnetic tape
one foot is equal to 12 inch
4 x 12 = 48
48/2 = 24 pictures i can paste
11.4 Weight in Customary Units
Find the equivalent weight.
Question 19.
4 T = ______ lb
Answer:
4 t = 8000lb
Explanation
one ton is equal to 2000 pounds
4 x 2000 = 8000 pounds
Question 20.
15 lb = _____ oz
Answer:
15 lb = 240 oz
Explanation:
one pound is equal to 16 ounce
15 x 16 = 240 ounce
there are 240 ounce in 15 pounds
Question 21.
12 lb = _____ oz
Answer:
12 lb = 192 oz
Explanation:
one pound is equal to 16 ounce
12 x 16 = 192 ounce
there are 192 ounce in 12 pounds
Question 22.
15 T = ______ lb
Answer:
15 t = 30000lb
Explanation
one ton is equal to 2000 pounds
15 x 2000 = 30000 pounds
Question 23.
2\(\frac{1}{2}\) lb = _____ oz
Answer:
one pound is equal to 16 ounce
2. 5 pound is equal to 40 ounce
Question 24.
\(\frac{3}{4}\) T = _____ lb
Answer:
1500 pounds
11.5 Capacity in Customary Units
Find the equivalent capacity.
Question 25.
6 pt = _____ c
Answer:
6 pt = 12 cups
Explanation:
one pint is equal to 2 cups
6 x 2 = 12 cups
so there are 12 cups in 6 pints
Question 26.
3 qt = ______ pt
Answer:
3 qt = 6 pt
Explanation:
one quart is equal to 2 pints
3 x2 = 6 pints
so there are 6 pints 3 quarts
Question 27.
9 gal = ______ qt
Answer:
9 gal = 36 quarts
Explanation:
one gallon is equal to 4 quarts
9 x 4 = 36 quarts
so there are 36 quarts in 9 gal
Question 28.
2 gal = ______ pt
Answer:
2 gal = 16 pt
Explanation:
one galllon is equal to 4 quarts
one quart is equal to 2 pints
2 x 4 = 8 quarts
8 x 2 = 16 pints
Question 29.
10\(\frac{3}{4}\) gal = ______ pt
Answer:
3 / 4 of one gallon
10. 75 gal is equal to 86 pints
Question 30.
6\(\frac{1}{2}\) pt = _____ c
Answer:
6 x 0.5= 6.5
6.5 x 2= 13 cups
11.6 Make and Interpret Line Plots
Question 31.
A scientist is studying the lengths of 15 sea horses. Make a line plot to display the data.
Answer:
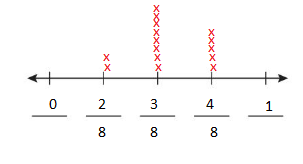
Question 32.
Precision
Use the line plot in Exercise 31. How many times as many \(\frac{3}{8}\)-inch sea horses are there as \(\frac{1}{4}\)-inch sea horses? Explain.

Answer: 8 times of 3/8 sea horses are there.
Question 33.
Reasoning
In Exercise 31, are most of the sea horses less than \(\frac{5}{8}\) inch long? Explain.
Answer:
each sea horse is greater than 5/8.
according to the table
11.7 Units of Time
Find the equivalent amount of time.
Question 34.
5 yr = _____ wk
Answer:
one year is equal to 52 week
5 x 52 = 260wk
Question 35.
15 min = _____ sec
Answer:
one minute is equal to 60 sec
15 x 60 = 900 sec
Question 36.
\(\frac{1}{3}\) d = _____ h
Answer:
one day is equal to 24 hours
24/ 3 = 8 hours.
Question 37.
1\(\frac{1}{2}\) yr = _____ wk
Answer:
one year is equal to 52 week
one and half year is equal to 76 wk
11.8 Problem Solving: Elapsed Time
Question 38.
A gymnastics competition is 2\(\frac{3}{4}\) hours long. The competition time is divided equally among 5 age groups. For how many minutes does each age group perform?

Answer:
each team participates 41 minutes long
11.9 Mixed Measures
Add or subtract
Question 39.
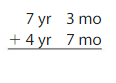
Answer:
11 yr 10 mo
Question 40.

Answer:
8 gal 1 qt
Question 41.

Answer:
11 pints 1 cup
Question 42.
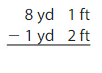
Answer:
6 yd 2 feet
one yard is equal to 3 feet.
Question 43.
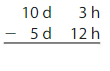
Answer: 4 days 15 h.
one day is equal to 24 hours
Question 44.

Answer:
8 miles 1651 yd
one mile is equal to 1760 yards
Understand Measurement Equivalence Cumulative Practice
Question 1.
Four laps around a track is equal to1 mile. You run 3 laps around the track. Which number line show show many miles you run?
Answer:
option b
Question 2.
When estimating to find the product of 25 and 32, which expressions will give an estimate that is greater than the product of 25 and 32?

Answer:
option a
Question 3.
A bottle of sand art is \(\frac{3}{8}\) full of purple sand and \(\frac{3}{8}\) full of blue sand. The rest of the bottle is full of green sand. How much of the bottle is filled with both purple sand and blue sand?

Answer:
option c
is true
Question 4.
Which statements are true?

Answer:
option c is wrong
Question 5.
Compare the fractions using benchmarks. Which comparisons are true?

Answer:
option b is wrong statement
Question 6.
What number is shown by the model?

Answer:
option c
5/10 = 0.5
Question 7.
Which fraction cannot be written as a mixed number?

Answer:
option d
Question 8.
What is the missing number in _____ ÷ 2 = 400?
A. 200
B. 800
C. 8,000
D. 600
Answer:
option b
800/ 2 = 400.
Question 9.
Which statements are true?

Answer:
option c
1000 m is equal to 1 kilometer
Question 10.
Multiply 2 × 3\(\frac{5}{6}\).
A. 6\(\frac{5}{6}\)
B. 7\(\frac{4}{6}\)
C. 5
D. \(\frac{5}{36}\)
Answer:
option a
Question 11.
Which one does not belong?
A. \(\frac{3}{10}\)
B. 0.30
C. 0.03
D. \(\frac{30}{100}\)
Answer:
option d
Question 12.
Which expression shows \(\frac{4}{3}\) as a sum of unit fractions?
Answer:
option d
4 / 3 is represented as 1 / 3 + 1 / 3 + 1/ 3 + 1 / 3.
Question 13.
Look at the dot pattern below. How many dots are in the 112th figure?

Answer: 448 dots
Question 14.
Which show 5 hundredths?

Answer:
option a 5/100
Question 15.
A child ticket costs $12 less than an adult ticket. In 1 day, 25 adult tickets and 34 child tickets are sold.

Part A How much money was raised from adult tickets?
Part B How much money was raised from child tickets?
Part C How much more money was raised from child tickets than from adult tickets? Explain.
Answer:
a. $65
b. $12
c. $ 53
Question 16.
Which measures are equivalent to8 gallons?

Answer:
32 quarts
Question 17.
You want to find 4 × 598 using the Distributive Property. You begin solving as shown. What is your next step?
4 × 598 = 4 × (600 – 2)
A. 4 × 600 × 2
B. (4 × 600) + (4 × 2)
C. (4 × 600) – (4 × 2)
D. (4 × 600) – 2
Answer:
option c
formula: a x (b – c)
4 (600-2)
4 x 600 – 4 x2
Question 18.
A recipe calls for \(\frac{3}{4}\) cup of peanut butter. You make 3 batches of the recipe. Which expressions show how many cups of peanut butter you use?

Answer:
3 x 3/4
option c
Understand Measurement Equivalence STEAM Performance Task
An electrical circuit is a pathway of wires that electricity can flow through. Many homes have an electrical panel that provides power to electrical circuits. The circuits are connected to electrical outlets throughout the home.
Question 1.
Watts are the measure of how much power a circuit can provide. Every electrical current has two components: volts and amps.
Watts = volts × amps

a. For a wire that carries 120 volts and 20 amps, how many watts of power are available?
b. For a wire that carries 240 volts and 15 amps, how many watts of power are available?
Answer:
a. watts = volts x amps
120 x 20 = 2400
2400 watts of power are available
b. watts = volts x amps
240 x 15= 3600
for a wire that carries 240 v and 15 a the power of watts available are 3600.
Question 2.
An electrician checks the circuits in your house.
a. One of the circuits has a maximum capacity of 15 amps. The electrician recommends that you only use \(\frac{4}{5}\) of the total amps on the circuit. How many amps should be used?
b. The wire from this 15-amp circuit carries 120 volts. How many watts should be used on this circuit?
c. Your toaster is plugged in to the 15-amp circuit. Use the table to find another appliance that can be used on the same circuit and stay within the recommended amount of amps.

d.Can you run the microwave and the refrigerator on the15-amp circuit? Explain.
Answer:
yes by the above table recordings
Question 3.
You are decorating for a party at your house.
a. There are 15 bulbs on a string of lights. Each bulb uses 12 watts of energy. How many watts of energy does one string of lights use?

b. You connect 7 strings of lights together. Can the lights be plugged into a 15-amp circuit, or is a 20-amp circuit needed? Explain.
c. The length of each string is 20\(\frac{3}{4}\) feet. What is the total length of all 7 strings of lights?
d. Five of the bulbs burn out. Of the bulbs that are lit, \(\frac{2}{10}\)are purple, \(\frac{1}{10}\) are blue, \(\frac{2}{10}\) are green, and the rest are red.What fraction of the bulbs are red?
e. How many more bulbs are purple than blue?
f. The lights are plugged in from 4:35 P.M. until 9:35 P.M. Each hour that the lights are on costs about $0.18 in electricity.What is the total cost to have the lights on for the party?
Answer:
a. one bulb = 8 watts
one string = 15 bulbs
8 x 15 = 120 watts
b. 7 x 120 = 840 watts make an ampire 15 amp wire is enough
1 amp = 120 watt
15 amp 15 x 120 = 1800 watt capacity circuit
c. 145
d. 0.2 are purple
0.1 is blue
0.2 are red
the fraction of the bulbs are red
e. 0.1bulbs are purple than blue
f. 5 x 0.18
= 5.08
is the total cost to have the lights on for the party
Conclusion:
We wish the information provided in this article regarding the Big Ideas Math Answers Grade 4 Chapter 11 Understand Measurement Equivalence Circumference, Area, and Volume is beneficial for all the students. Make use of the given links and practice well for the exams. If you have any queries about Big Ideas Math Answers Grade 4 Chapter 11 Understand Measurement Equivalence you can post your comments in the below section.