Looking for online help regarding the concepts of Big Ideas Math Algebra 2 Chapter 9 Trigonometric Ratios and Functions? Don’t Panic and we are with you in this and created Trigonometric Ratios and Functions Big Ideas Math Book Algebra 2 Ch 9 Solution Key aligned as per the BIM Algebra 2 Textbooks. Practice the Questions available here from Exercises, Chapter Tests, Cumulative Assessments, Review Tests, etc., and become pro in the subject.
Trigonometric Ratios and Functions Big Ideas Math Algebra 2 Answers for Ch 9 available helps you to be prepared for the exam. Solving the Big Ideas Math Algebra 2 Chapter 9 Answer Key regularly improves your level of understanding of the related concepts. In fact, your speed and accuracy will be improvised which in turn helps you to stand out from the crowd and clear the final exams with higher scores.
Big Ideas Math Book Algebra 2 Answer Key Chapter 9 Trigonometric Ratios and Functions
Improve your subject knowledge that you have always dreamt of by referring to our Big Ideas Math Book Algebra 2 Ch 9 Trigonometric Ratios and Functions Answers. Enhance your math proficiency by taking the help of the BIM Algebra 2 Chapter 9 Trigonometric Ratios and Functions Solution Key. Kick start your preparation using the preparation guide BIM Algebra 2 Chapter 9 Answers and improve your overall knowledge. You can access the Topicwise Big Ideas Math Algebra 2 Chapter 9 Solutions without paying a single penny through the below available quick links. All you have to do is tap on them to learn about the respective topic in detail.
- Trigonometric Ratios and Functions Maintaining Mathematical Proficiency – Page 459
- Trigonometric Ratios and Functions Mathematical Practices – Page 460
- Lesson 9.1 Right Triangle Trigonometry – Page(461-468)
- Right Triangle Trigonometry 9.1 Exercises – Page(466-468)
- Lesson 9.2 Angles and Radian Measure – Page(469-476)
- Angles and Radian Measure 9.2 Exercises – Page(474-476)
- Lesson 9.3 Trigonometric Functions of Any Angle – Page(477-484)
- Trigonometric Functions of Any Angle 9.3 Exercises – Page(482-484)
- Lesson 9.4 Graphing Sine and Cosine Functions – Page(485-494)
- Graphing Sine and Cosine Functions 9.4 Exercises – Page(491-494)
- Trigonometric Ratios and Functions Study Skills: Form a Final Exam Study Group – Page 495
- Trigonometric Ratios and Functions 9.1–9.4 Quiz – Page 496
- Lesson 9.5 Graphing Other Trigonometric Functions – Page(497-504)
- Graphing Other Trigonometric Functions 9.5 Exercises – Page(502-504)
- Lesson 9.6 Modeling with Trigonometric Functions – Page(505-512)
- Modeling with Trigonometric Functions 9.6 Exercises – Page(510-512)
- Lesson 9.7 Using Trigonometric Identities – Page(513-518)
- Using Trigonometric Identities 9.7 Exercises – Page(517-518)
- Lesson 9.8 Using Sum and Difference Formulas – Page(519-524)
- Using Sum and Difference Formulas 9.8 Exercises – Page(523-524)
- Trigonometric Ratios and Functions Performance Task: Lightening the Load – Page 525
- Trigonometric Ratios and Functions Chapter Review – Page(526-530)
- Trigonometric Ratios and Functions Chapter Test – Page 531
- Trigonometric Ratios and Functions Cumulative Assessment – Page(532 – 533)
Trigonometric Ratios and Functions Maintaining Mathematical Proficiency
Order the expressions by value from least to greatest.
Question 1.
∣4∣, |2 − 9∣, ∣6 + 4∣, − ∣7∣
Answer:
− ∣7∣, ∣4∣, |2 − 9∣, ∣6 + 4∣
Explanation:
∣4∣ = 4
|2 − 9∣ = |-7| = 7
∣6 + 4∣ = 10
− ∣7∣ = -7
Question 2.
∣9 − 3∣, ∣0∣, ∣−4∣, \(\frac{|-5|}{|2|}\)
Answer:
∣0∣, \(\frac{|-5|}{|2|}\), ∣−4∣, ∣9 − 3∣
Explanation:
∣9 − 3∣ = 6
∣0∣ = 0
∣−4∣ = 4
\(\frac{|-5|}{|2|}\) = 2.5
Question 3.
∣−83∣,∣−2 • 8 ∣, ∣9 − 1∣, ∣9∣ + ∣−2∣ − ∣1 ∣
Answer:
∣9 − 1∣, ∣9∣ + ∣−2∣ − ∣1 ∣, ∣−2 • 8 ∣, ∣−83∣
Explanation:
∣−83∣ = 512
∣−2 • 8 ∣ = 16
∣9 − 1∣ = 8
∣9∣ + ∣−2∣ − ∣1 ∣ = 9 + 2 – 1 = 10
Question 4.
∣−4 + 20∣, −∣42∣, ∣5∣−∣3 • 2 ∣, ∣−15∣
Answer:
−∣42∣, ∣5∣−∣3 • 2 ∣ , ∣−15∣, ∣−4 + 20∣
Explanation:
∣−4 + 20∣ = 16
−∣42∣ = -16
∣5∣−∣3 • 2 ∣ = 5 – 6 = -1
∣−15∣ = 15
Find the missing side length of the triangle.
Question 5.

Answer:
c = 13
Explanation:
c² = 5² + 12²
c² = 25 + 144
c = 13
Question 6.
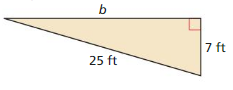
Answer:
b = 24
Explanation:
25² = b² + 7²
625 – 49 = b²
b = 24
Question 7.
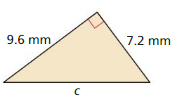
Answer:
c = 12
Explanation:
c² = 7.2² + 9.6²
c² = 51.84 + 92.16
c = 12
Question 8.
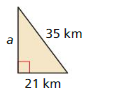
Answer:
a = 28
Explanation:
35² = a² + 21²
a² = 1225 – 441
a = 28
Question 9.

Answer:
a = 11.66
Explanation:
(12.3)² = a² + 4²
a² = 136.11
a = 11.66
Question 10.
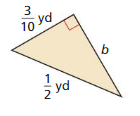
Answer:
b = 0.4
Explanation:
0.5² = 0.3² +b²
b² = 0.25 – 0.09
b = 0.4
Question 11.
ABSTRACT REASONING
The line segments connecting the points (x1, y1), (x2, y1), and (x2, y2) form a triangle. Is the triangle a right triangle? Justify your answer.
Answer:
AB = (x₂ – x₁)
BC = (y₂ – y₁)
AC = √(x₂ – x₁)² + (y₂ – y₁)²
AC² = (x₂ – x₁)² + (y₂ – y₁)² = AB² + BC²
So the points form a right triangle.
Trigonometric Ratios and Functions Mathematical Practices
Mathematically proficient students reason quantitatively by creating valid representations of problems.
Monitoring Progress
Find the exact coordinates of the point (x, y) on the unit circle.
Question 1.
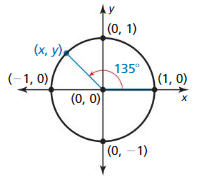
Answer:
(x, y) = (-0.707, 0.707)
Explanation:
A = 135
(x, y) = (cos A, sin A)
= (cos 135, sin 135)
= (-0.707, 0.707)
Question 2.
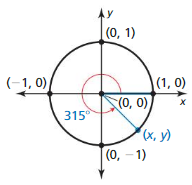
Answer:
(x, y) = (0.707, -0.707)
Explanation:
A = 315
(x, y) = (cos A, sin A)
= (cos 315, sin 315)
= (0.707, -0.707)
Question 3.
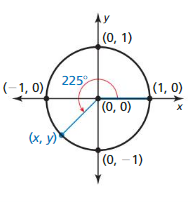
Answer:
(x, y) = (-0.707, 0.707)
Explanation:
A = 225
(x, y) = (cos A, sin A)
= (cos 225, sin 225)
= (-0.707, 0.707)
Lesson 9.1 Right Triangle Trigonometry
Essential Question How can you find a trigonometric function of an acute angle θ?
Consider one of the acute angles θ of a right triangle. Ratios of a right triangle’s side lengths are used to define the six trigonometric functions, as shown.

EXPLORATION 1
Trigonometric Functions of Special Angles
Work with a partner. Find the exact values of the sine, cosine, and tangent functions for the angles 30°, 45°, and 60° in the right triangles shown.

EXPLORATION 2
Exploring Trigonometric Identities
Work with a partner.

Use the definitions of the trigonometric functions to explain why each trigonometric identity is true.
a. sin θ = cos(90° − θ)
b. cos θ = sin(90° − θ)
c. sin θ =\(\frac{1}{\csc \theta}\)
d. tan θ = \(\frac{1}{\cot \theta}\)
Use the definitions of the trigonometric functions to complete each trigonometric identity.
![]()
Communicate Your Answer
Question 3.
How can you find a trigonometric function of an acute angle θ?
Answer:
Question 4.
Use a calculator to find the lengths x and y of the legs of the right triangle shown.
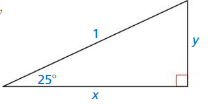
Answer:
sin 25 = y
y = 0.422
cos 25 = x
x = 0.906
Monitoring Progress
Evaluate the six trigonometric functions of the angle θ.
Question 1.
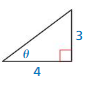
Answer:
sin θ = \(\frac { 3 }{ 5 } \)
cos θ = \(\frac { 4 }{ 5 } \)
tan θ = \(\frac { 3 }{ 4 } \)
cot θ = \(\frac { 4 }{ 3 } \)
sec θ = \(\frac { 5 }{ 3 } \)
csc θ = \(\frac { 5 }{ 4 } \)
Explanation:
hypotenuse = √4² + 3² = 5
opposite side = 3
adjacent side = 4
sin θ = \(\frac { opposite side }{ hypotenuse } \) = \(\frac { 3 }{ 5 } \)
cos θ = \(\frac { adjacent side }{ hypotenuse } \) = \(\frac { 4 }{ 5 } \)
tan θ = \(\frac { opposite side }{ adjacent side } \) = \(\frac { 3 }{ 4 } \)
cot θ = \(\frac { adjacent side }{ opposite side } \) = \(\frac { 4 }{ 3 } \)
sec θ = \(\frac { hypotenuse }{ adjacent side } \) = \(\frac { 5 }{ 3 } \)
csc θ = \(\frac { hypotenuse }{ opposite side } \) = \(\frac { 5 }{ 4 } \)
Question 2.

Answer:
sin θ = \(\frac { 15 }{ 17 } \)
cos θ = \(\frac { 8 }{ 17 } \)
tan θ = \(\frac { 15 }{ 8 } \)
cot θ = \(\frac { 8 }{ 15 } \)
sec θ = \(\frac { 17 }{ 8 } \)
csc θ = \(\frac { 17 }{ 15 } \)
Explanation:
hypotenuse = 17
opposite side = 15
17² = 15² + x²
x = 8
adjacent side = 8
sin θ = \(\frac { opposite side }{ hypotenuse } \) = \(\frac { 15 }{ 17 } \)
cos θ = \(\frac { adjacent side }{ hypotenuse } \) = \(\frac { 8 }{ 17 } \)
tan θ = \(\frac { opposite side }{ adjacent side } \) = \(\frac { 15 }{ 8 } \)
cot θ = \(\frac { adjacent side }{ opposite side } \) = \(\frac { 8 }{ 15 } \)
sec θ = \(\frac { hypotenuse }{ adjacent side } \) = \(\frac { 17 }{ 8 } \)
csc θ = \(\frac { hypotenuse }{ opposite side } \) = \(\frac { 17 }{ 15 } \)
Question 3.
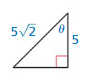
Answer:
sin θ = \(\frac { 1 }{ √2 } \)
cos θ = \(\frac { 1 }{ √2 } \)
tan θ = 1
cot θ = 1
sec θ = √2
csc θ = √2
Explanation:
hypotenuse = 5√2
opposite side = 5
adjacent side = 5
50 = x² + 25
x = 5
sin θ = \(\frac { opposite side }{ hypotenuse } \) = \(\frac { 5 }{ 5√2 } \)
= \(\frac { 1 }{ √2 } \)
cos θ = \(\frac { adjacent side }{ hypotenuse } \) = \(\frac { 5 }{ 5√2 } \)
= \(\frac { 1 }{ √2 } \)
tan θ = \(\frac { opposite side }{ adjacent side } \) = \(\frac { 5 }{ 5 } \) = 1
cot θ = \(\frac { adjacent side }{ opposite side } \) = \(\frac { 5 }{ 5 } \) = 1
sec θ = \(\frac { hypotenuse }{ adjacent side } \) = \(\frac { 5√2 }{ 5 } \) = √2
csc θ = \(\frac { hypotenuse }{ opposite side } \) = \(\frac { 5√2 }{ 5 } \) = √2
Question 4.
In a right triangle, θ is an acute angle and cos θ = \(\frac{7}{10}\). Evaluate the other five trigonometric functions of θ.
Answer:
sin θ = \(\frac { √51 }{ 10 } \)
tan θ = \(\frac { √51 }{ 7 } \)
cot θ = \(\frac { 7 }{ √51 } \)
sec θ = \(\frac { 10 }{ 7 } \)
csc θ = \(\frac { 10 }{ √51 } \)
Explanation:
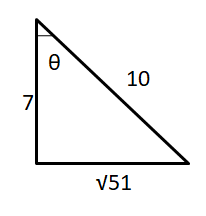
10² = 7² + x²
x² = 100 – 49 = 51
x = √51
adjacent side = 7
hypotenuse = 10
opposite side = √51
cos θ = \(\frac{7}{10}\)
So, sec θ = \(\frac { hypotenuse }{ adjacent side } \) = \(\frac{10}{7}\)
sin θ = \(\frac { opposite side }{ hypotenuse } \) = \(\frac { √51 }{ 10 } \)
tan θ = \(\frac { opposite side }{ adjacent side } \) = \(\frac { √51 }{ 7 } \)
cot θ = \(\frac { adjacent side }{ opposite side } \) = \(\frac { 7 }{ √51 } \)
csc θ = \(\frac { hypotenuse }{ opposite side } \) = \(\frac { 10 }{ √51 } \)
Question 5.
Find the value of x for the right triangle shown.
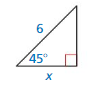
Answer:
x = 3√2
Explanation:
cos 45° = \(\frac { x }{ 6 } \)
\(\frac { √2 }{ 2 } \) = \(\frac { x }{ 6 } \)
x = 3√2
Solve △ABC using the diagram at the left and the given measurements.
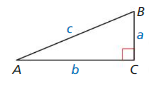
Question 6.
B = 45°, c = 5
Answer:
b = \(\frac { 5√2 }{ 2 } \), a = \(\frac { 5√2 }{ 2 } \), A = 45°
Explanation:
sin 45° = \(\frac { b }{ c } \)
\(\frac { √2 }{ 2 } \) = \(\frac { b }{ 5 } \)
b = \(\frac { 5√2 }{ 2 } \)
cos 45° = \(\frac { a }{ c } \)
\(\frac { √2 }{ 2 } \) = \(\frac { a }{ 5 } \)
a = \(\frac { 5√2 }{ 2 } \)
A = 180 – (90 + 45)
A = 45
Question 7.
A = 32°, b = 10
Answer:
a = 6.23, c = 11.79, B = 58°
Explanation:
cos 32° = \(\frac { b }{ c } \)
0.848 = \(\frac { 10 }{ c } \)
c = 11.79
sin 32° = \(\frac { a }{ c } \)
0.529 = \(\frac { a }{ 11.79 } \)
a = 6.23
B = 180 – (90 + 32)
B = 58
Question 8.
A = 71°, c = 20
Answer:
a = 6.5, B = 19°, b = 18.9
Explanation:
B = 180 – (90 + 71)
= 19°
sin 19° = \(\frac { a }{ c } \)
0.325 = \(\frac { a }{ 20 } \)
a = 6.5
cos 19° = \(\frac { b }{ c } \)
0.945 = \(\frac { b }{ 20 } \)
b = 18.9
Question 9.
B = 60°, a = 7
Answer:
A = 30°, b = 4.04, c = 8.08
Explanation:
A = 180 – (90 + 60)
A = 30°
sin 60° = \(\frac { a }{ c } \)
0.866 = \(\frac { 7 }{ c } \)
c = 8.08
cos 60° = \(\frac { b }{ c } \)
0.5 = \(\frac { b }{ 8.08 } \)
b = 4.04
Question 10.
In Example 5, find the distance between B and C.
Answer:
BC = 2√17
Explanation:
Given that
AB = 2 mi
AC = 8 mi
BC² = AB² + AC²
= 2² + 8² = 4 + 64
BC = 2√17
Question 11.
WHAT IF?
In Example 6, estimate the height of the parasailer above the boat when the angle of elevation is 38°.
Answer:
The height of the parasailer is 44.28 ft.
Explanation:
sin 38° = \(\frac { h }{ 72 } \)
0.615 = \(\frac { h }{ 72 } \)
h = 44.28
Right Triangle Trigonometry 9.1 Exercises
Vocabulary and Core Concept Check
Question 1.
COMPLETE THE SENTENCE
In a right triangle, the two trigonometric functions of θ that are defined using the lengths of the hypotenuse and the side adjacent to θ are __________ and __________.
Answer:

Question 2.
VOCABULARY
Compare an angle of elevation to an angle of depression.
Answer:
An angle of elevation is the angle between the horizontal line of sight and the object. Angle of depression is the angle between the horizontal line of sight and the object.
Question 3.
WRITING
Explain what it means to solve a right triangle.
Answer:
Question 4.
DIFFERENT WORDS, SAME QUESTION
Which is different? Find “both” answers.

Answer:
What is the ratio of the side opposite θ to the hypotenuse?
Explanation:
csc θ = \(\frac { hypotenuse }{ opposite side } \) = \(\frac { 6 }{ 4 } \)
sin θ = \(\frac { Opposite side }{ hypotenuse } \) = \(\frac { 4 }{ 6 } \)
\(\frac { 1 }{ sin θ} \) = \(\frac { 3}{ 2 } \)
The ratio of side opposite θ to hypotenuse is sinθ
the ratio of hypotenuse to the side opposite θ is cscθ
Monitoring Progress and Modeling with Mathematics
In Exercises 5–10, evaluate the six trigonometric functions of the angle θ.
Question 5.

Answer:

Question 6.
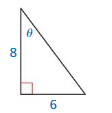
Answer:
sin θ = \(\frac { 3 }{ 5 } \)
cos θ = \(\frac { 4 }{ 5 } \)
tan θ = \(\frac { 3 }{ 4 } \)
cot θ = \(\frac { 4 }{ 3 } \)
sec θ = \(\frac { 5 }{ 4 } \)
csc θ = \(\frac { 5 }{ 3 } \)
Explanation:
x² = 8² + 6²
x = 10
hypotenuse = 10
opposite side = 6
adjacent side = 8
sin θ = \(\frac { opposite side }{ hypotenuse } \) = \(\frac { 6 }{ 10 } \)
cos θ = \(\frac { adjacent side }{ hypotenuse } \) = \(\frac { 8 }{ 10 } \)
tan θ = \(\frac { opposite side }{ adjacent side } \) = \(\frac { 6 }{ 8 } \)
cot θ = \(\frac { adjacent side }{ opposite side } \) = \(\frac { 8 }{ 6 } \)
sec θ = \(\frac { hypotenuse }{ adjacent side } \) = \(\frac { 10 }{ 8 } \)
csc θ = \(\frac { hypotenuse }{ opposite side } \) = \(\frac { 10 }{ 6 } \)
Question 7.
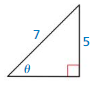
Answer:

Question 8.
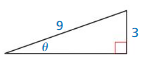
Answer:
sin θ = \(\frac { 1 }{ 3 } \)
cos θ = \(\frac { 2√2 }{ 3 } \)
tan θ = \(\frac { √2 }{ 4 } \)
cot θ = \(\frac { 4 }{ √2 } \)
sec θ = \(\frac { 3 }{ 2√2 } \)
csc θ = 3
Explanation:
hypotenuse = 9
opposite side = 3
9² = 3² + x²
x = 6√2
adjacent side = 6√2
sin θ = \(\frac { opposite side }{ hypotenuse } \) = \(\frac { 3 }{ 9 } \)
cos θ = \(\frac { adjacent side }{ hypotenuse } \) = \(\frac { 6√2 }{ 9 } \)
tan θ = \(\frac { opposite side }{ adjacent side } \) = \(\frac { 3 }{ 6√2 } \)
cot θ = \(\frac { adjacent side }{ opposite side } \) = \(\frac { 6√2 }{ 3 } \)
sec θ = \(\frac { hypotenuse }{ adjacent side } \) = \(\frac { 9 }{ 6√2 } \)
csc θ = \(\frac { hypotenuse }{ opposite side } \) = \(\frac { 9 }{ 3 } \)
Question 9.
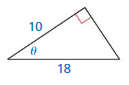
Answer:

Question 10.
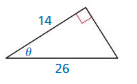
Answer:
sin θ = \(\frac { 2√30 }{ 13 } \)
cos θ = \(\frac { 7 }{ 13 } \)
tan θ = \(\frac { 2√30 }{ 7 } \)
cot θ = \(\frac { 7 }{ 2√30 } \)
sec θ = \(\frac { 13 }{ 7 } \)
csc θ = \(\frac { 13 }{ 2√30 } \)
Explanation:
hypotenuse = 26
26² = 14² + x²
x = 4√30
adjacent side = 14
opposite side = 4√30
sin θ = \(\frac { opposite side }{ hypotenuse } \) = \(\frac { 4√30 }{ 26 } \)
cos θ = \(\frac { adjacent side }{ hypotenuse } \) = \(\frac { 14 }{ 26 } \)
tan θ = \(\frac { opposite side }{ adjacent side } \) = \(\frac { 4√30 }{ 14 } \)
cot θ = \(\frac { adjacent side }{ opposite side } \) = \(\frac { 14 }{ 4√30 } \)
sec θ = \(\frac { hypotenuse }{ adjacent side } \) = \(\frac { 26 }{ 14 } \)
csc θ = \(\frac { hypotenuse }{ opposite side } \) = \(\frac { 26 }{ 4√30 } \)
Question 11.
REASONING
Let θ be an acute angle of a right triangle. Use the two trigonometric functions tan θ = \(\frac{4}{9}\) and sec θ = \(\frac{\sqrt{97}}{9}\) to sketch and label the right triangle. Then evaluate the other four trigonometric functions of θ.
Answer:
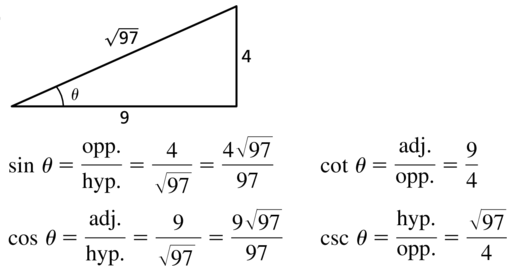
Question 12.
ANALYZING RELATIONSHIPS
Evaluate the six trigonometric functions of the 90° − θ angle in Exercises 5–10. Describe the relationships you notice.
Answer:
sin( 90° − θ) = cosθ
cos( 90° − θ) = sinθ
tan( 90° − θ) = cotθ
cot( 90° − θ) = tanθ
sec( 90° − θ) = cscθ
csc( 90° − θ) = secθ
In Exercises 13–18, let θ be an acute angle of a right triangle. Evaluate the other five trigonometric functions of θ.
Question 13.
sin θ = \(\frac{7}{11}\)
Answer:


Question 14.
cos θ = \(\frac{5}{12}\)
Answer:
sin θ = \(\frac{√119}{12}\)
tan θ = \(\frac{√119}{5}\)
cot θ = \(\frac{5}{√119}\)
sec θ = \(\frac{12}{5}\)
csc θ = \(\frac{12}{√119}\)
Explanation:
cos θ = \(\frac{5}{12}\)
sec θ = \(\frac{12}{5}\)
hypotenuse = 12, adjacent side = 5
12² = 5² + x²
x = √119
opposite side = √119
sin θ = \(\frac{√119}{12}\)
tan θ = \(\frac{√119}{5}\)
cot θ = \(\frac{5}{√119}\)
csc θ = \(\frac{12}{√119}\)
Question 15.
tan θ = \(\frac{7}{6}\)
Answer:


Question 16.
csc θ = \(\frac{15}{8}\)
Answer:
sin θ = \(\frac{8}{15}\)
cos θ = \(\frac{√161}{15}\)
tan θ = \(\frac{8}{√161}\)
cot θ = \(\frac{√161}{8}\)
sec θ = \(\frac{15}{√161}\)
Explanation:
csc θ = \(\frac{15}{8}\)
sin θ = \(\frac{8}{15}\)
hypotenuse = 15, opposite side = 8
x² = 15² – 8²
x = √161
cos θ = \(\frac{√161}{15}\)
tan θ = \(\frac{8}{√161}\)
cot θ = \(\frac{√161}{8}\)
sec θ = \(\frac{15}{√161}\)
Question 17.
sec θ = \(\frac{14}{9}\)
Answer:

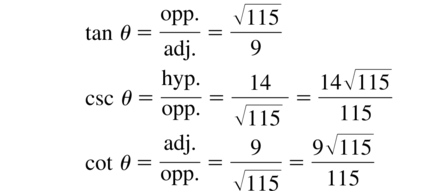
Question 18.
cot θ = \(\frac{16}{11}\)
Answer:
sin θ = \(\frac{11}{√377}\)
cos θ = \(\frac{16}{√377}\)
sec θ = \(\frac{√377}{16}\)
csc θ = \(\frac{√377}{11}\)
tan θ = \(\frac{11}{16}\)
Explanation:
cot θ = \(\frac{16}{11}\)
tan θ = \(\frac{11}{16}\)
Opposite side = 11, adjacent side = 16
x² = 11² + 16²
x = √377
hypotenuse = √377
sin θ = \(\frac{11}{√377}\)
cos θ = \(\frac{16}{√377}\)
sec θ = \(\frac{√377}{16}\)
csc θ = \(\frac{√377}{11}\)
Question 19.
ERROR ANALYSIS
Describe and correct the error in finding sin θ of the triangle below.
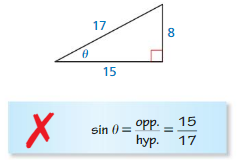
Answer:

Question 20.
ERROR ANALYSIS
Describe and correct the error in finding csc θ, given that θ is an acute angle of a right triangle and cos θ = \(\frac{7}{11}\).

Answer:
adjacent side = 7, hypotenuse = 11
opposite side = √(11² – 7²) = 6√2
sin θ = \(\frac{6√2}{11}[/latex
csc θ = [latex]\frac{1}{sin θ}\)
= \(\frac{11}{6√2}\)
In Exercises 21–26, find the value of x for the right triangle.
Question 21.
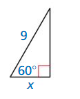
Answer:

Question 22.

Answer:
x = 3
Explanation:
cos 60° = \(\frac{x}{6}\)
0.5 = \(\frac{x}{6}\)
x = 3
Question 23.
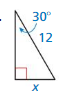
Answer:

Question 24.
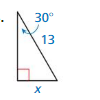
Answer:
x = 6.5
Explanation:
sin 30° = \(\frac{x}{13}\)
0.5 = \(\frac{x}{13}\)
x = 6.5
Question 25.
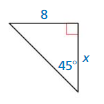
Answer:

Question 26.
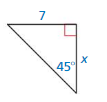
Answer:
x = 7
Explanation:
tan 45° = \(\frac{7}{x}\)
1 = \(\frac{7}{x}\)
x = 7
USING TOOLS In Exercises 27–32, evaluate the trigonometric function using a calculator. Round your answer to four decimal places.
Question 27.
cos 14°
Answer:
![]()
Question 28.
tan 31°
Answer:
tan 31° = 0.6008
Question 29.
csc 59°
Answer:

Question 30.
sin 23°
Answer:
sin 23° = 0.3907
Question 31.
cot 6°
Answer:
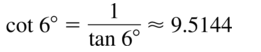
Question 32.
sec 11°
Answer:
sec 11° = 1.0187
In Exercises 33–40, solve △ABC using the diagram and the given measurements.
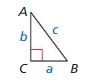
Question 33.
B = 36°, a = 23
Answer:

Question 34.
A = 27°, b = 9
Answer:
B = 63°, a = 4.59, c = 10.11
Explanation:
B = 180 – (90 + 27) = 63
tan 63° = \(\frac { 9 }{ a } \)
1.96 = \(\frac { 9 }{ a } \)
a = 4.59
sec 63° = \(\frac { c }{ 4.59 } \)
2.203 = \(\frac { c }{ 4.59 } \)
c = 10.11
Question 35.
A = 55°, a = 17
Answer:

Question 36.
B = 16°, b = 14
Answer:
A = 74°, a = 48.95, c = 50.93
Explanation:
A = 180 – (90 + 16) = 74
tan 16° = \(\frac { b }{ a } \)
0.286 = \(\frac { 14 }{ a } \)
a = 48.95
sec 16° = \(\frac { c }{ a} \)
1.04 = \(\frac { c }{ 48.95 } \)
c = 50.93
Question 37.
A = 43°, b = 31
Answer:

Question 38.
B = 31°, a = 23
Answer:
b = 13.8, c = 26.83, A = 59°
Explanation:
A = 180 – (90 + 31) = 59
tan 31° = \(\frac { b }{ a } \)
0.6 = \(\frac { b }{ 23 } \)
b = 13.8
sec 31° = \(\frac { c }{ a} \)
1.166 = \(\frac { c }{ 23 } \)
c = 26.83
Question 39.
B = 72°, c = 12.8
Answer:

Question 40.
A = 64°, a = 7.4
Answer:
B = 26°, c = 8.24, b = 3.552
Explanation:
B = 180 – (90 + 64) = 26
sec 26° = \(\frac { c }{ a} \)
sec 26° = \(\frac { c }{ 7.4} \)
1.11 = \(\frac { c }{ 7.4} \)
c = 8.24
tan 26° = \(\frac { b }{ a } \)
0.48 = \(\frac { b }{ 7.4 } \)
b = 3.552
Question 41.
MODELING WITH MATHEMATICS
To measure the width of a river, you plant a stake on one side of the river, directly across from a boulder. You then walk 100 meters to the right of the stake and measure a 79° angle between the stake and the boulder. What is the width w of the river?
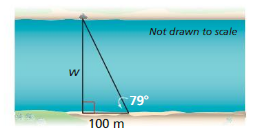
Answer:

Question 42.
MODELING WITH MATHEMATICS
Katoomba Scenic Railway in Australia is the steepest railway in the world. The railway makes an angle of about 52° with the ground. The railway extends horizontally about 458 feet. What is the height of the railway?
Answer:
The height of the railway is 581.66 ft
Explanation:

tan 52 = \(\frac { h }{ 458 } \)
1.27 = \(\frac { h }{ 458 } \)
h = 581.66
The height of the railway is 581.66 ft
Question 43.
MODELING WITH MATHEMATICS
A person whose eye level is 1.5 meters above the ground is standing 75 meters from the base of the Jin Mao Building in Shanghai, China. The person estimates the angle of elevation to the top of the building is about 80°. What is the approximate height of the building?
Answer:

Question 44.
MODELING WITH MATHEMATICS
The Duquesne Incline in Pittsburgh, Pennsylvania, has an angle of elevation of 30°. The track has a length of about 800 feet. Find the height of the incline.
Answer:
The height of the incline is 400 ft.
Explanation:
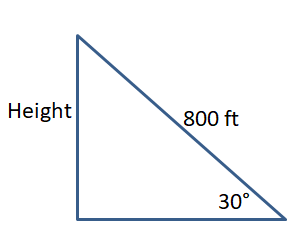
sin 30° = \(\frac { h }{ 800 } \)
0.5 = \(\frac { h }{ 800 } \)
h = 400
Question 45.
MODELING WITH MATHEMATICS
You are standing on the Grand View Terrace viewing platform at Mount Rushmore, 1000 feet from the base of the monument.

a. You look up at the top of Mount Rushmore at an angle of 24°. How high is the top of the monument from where you are standing? Assume your eye level is 5.5 feet above the platform.
b. The elevation of the Grand View Terrace is 5280 feet. Use your answer in part (a) to find the elevation of the top of Mount Rushmore.
Answer:

Question 46.
WRITING
Write a real-life problem that can be solved using a right triangle. Then solve your problem.
Answer:
Question 47.
MATHEMATICAL CONNECTIONS
The Tropic of Cancer is the circle of latitude farthest north of the equator where the Sun can appear directly overhead. It lies 23.5° north of the equator, as shown.
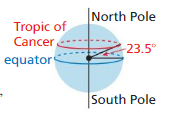
a. Find the circumference of the Tropic of Cancer using 3960 miles as the approximate radius of Earth.
b. What is the distance between two points on the Tropic of Cancer that lie directly across from each other?
Answer:

Question 48.
HOW DO YOU SEE IT?
Use the figure to answer each question.
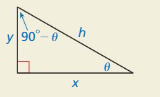
a. Which side is adjacent to θ?
b. Which side is opposite of θ?
c. Does cos θ = sin(90° − θ)? Explain.
Answer:
a. The side adjacent to θ is x
b. The side opposite to θ is y
c. Yes, cos θ = sin(90° − θ)
Because cos θ = \(\frac { x }{ h } \)
sin(90° − θ) = \(\frac { x }{ h } \)
Question 49.
PROBLEM SOLVING
A passenger in an airplane sees two towns directly to the left of the plane.
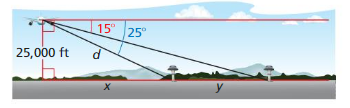
a. What is the distance d from the airplane to the first town?
b. What is the horizontal distance x from the airplane to the first town?
c. What is the distance y between the two towns? Explain the process you used to find your answer.
Answer:

Question 50.
PROBLEM SOLVING
You measure the angle of elevation from the ground to the top of a building as 32°. When you move 50 meters closer to the building, the angle of elevation is 53°. What is the height of the building?
Answer:
The height of the building is 59 m
Explanation:
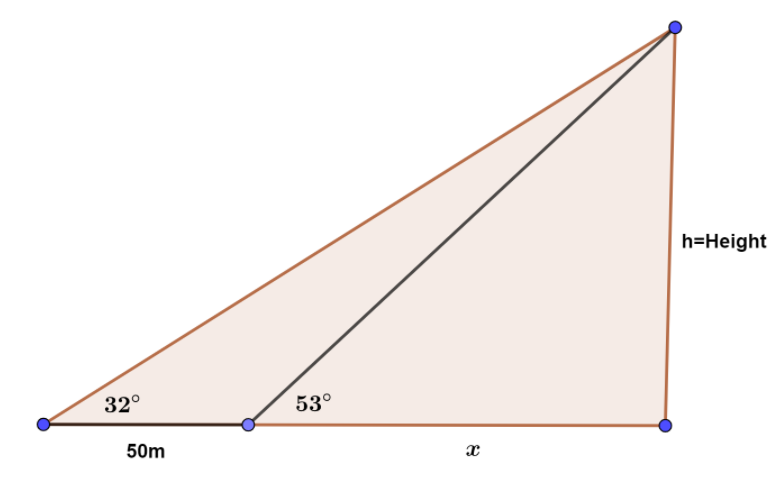
tan 32° = \(\frac { h }{ x + 50 } \) — (1)
tan 53° =
\(\frac { h }{ x } \)
1.327 = \(\frac { h }{ x } \)
1.327x = h
Substitute 1.327x = h in (1)
0.624 = \(\frac { 1.327x }{ x + 50 } \)
(x + 50) x 0.624 = 1.327x
x = 44.49
h = 1.327 x 44.49 = 59.04
The height of the building is 59 m
Question 51.
MAKING AN ARGUMENT
Your friend claims it is possible to draw a right triangle so the values of the cosine function of the acute angles are equal. Is your friend correct? Explain your reasoning.
Answer:
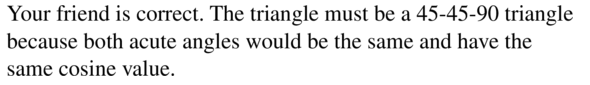
Question 52.
THOUGHT PROVOKING
Consider a semicircle with a radius of 1 unit, as shown below. Write the values of the six trigonometric functions of the angle θ. Explain your reasoning.
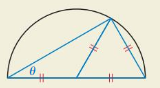
Answer:
Question 53.
CRITICAL THINKING
A procedure for approximating π based on the work of Archimedes is to inscribe a regular hexagon in a circle.

a. Use the diagram to solve for x. What is the perimeter of the hexagon?
b. Show that a regular n-sided polygon inscribed in acircle of radius 1 has a perimeter of 2n • sin (\(\frac{180}{n}\))°.
c. Use the result from part (b) to find an expression in terms of n that approximates π. Then evaluate the expression when n= 50.
Answer:

Maintaining Mathematical Proficiency.
Perform the indicated conversion.
Question 54.
5 years to seconds
Answer:
5 years = 5 x 365 x 24 x 60 x 60 = 157680000 seconds
Question 55.
12 pints to gallons
Answer:
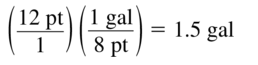
Question 56.
5.6 meters to millimeters
Answer:
5.6 x 1000 = 5600 millimeters
Find the circumference and area of the circle with the given radius or diameter.
Question 57.
r = 6 centimeters
Answer:
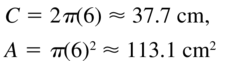
Question 58.
r = 11 inches
Answer:
Circumference is 69.11 in
Area is 380.132 in²
Explanation:
r = 11
C = 2π(11) = 69.11
A = π(11)² = 380.132
Question 59.
d = 14 feet
Answer:
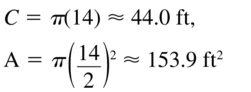
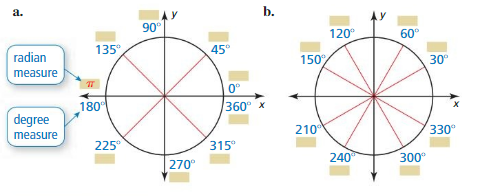
Lesson 9.2 Angles and Radian Measure
Essential Question How can you find the measure of an angle in radians?
Let the vertex of an angle be at the origin, with one side of the angle on the positive x-axis. The radian measure of the angle is a measure of the intercepted arc length on a circle of radius 1. To convert between degree and radian measure, use the fact that \(\frac{\pi \text { radians }}{180^{\circ}}\) = 1.
EXPLORATION 1
Writing Radian Measures of Angles
Work with a partner. Write the radian measure of each angle with the given degree measure. Explain your reasoning.
EXPLORATION 2
Writing Degree Measures of Angles
Work with a partner. Write the degree measure of each angle with the given radian measure. Explain your reasoning.

Communicate Your Answer
Question 3.
How can you find the measure of an angle in radians?
Answer:
Question 4.
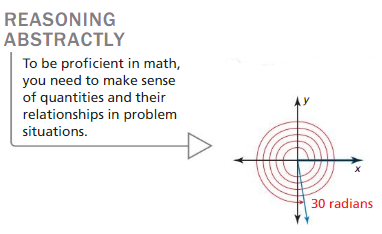
The figure shows an angle whose measure is 30 radians. What is the measure of the angle in degrees? How many times greater is 30 radians than 30 degrees? Justify your answers.
Answer:
Monitoring Progress
Draw an angle with the given measure in standard position.
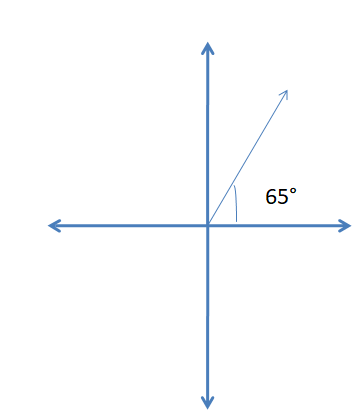
Question 1.
65°
Answer:
Question 2.
300°
Answer:
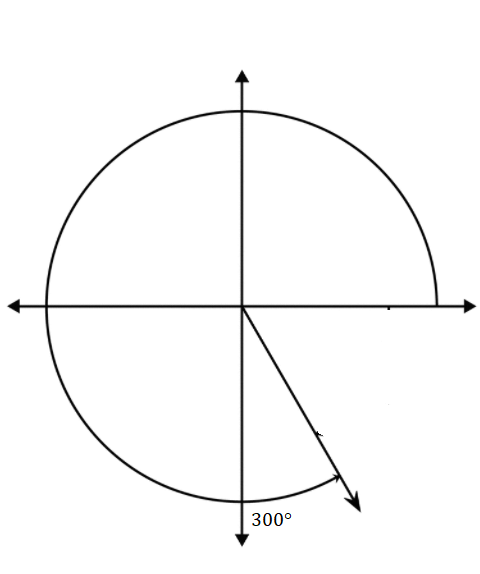
Question 3.
−120°
Answer:
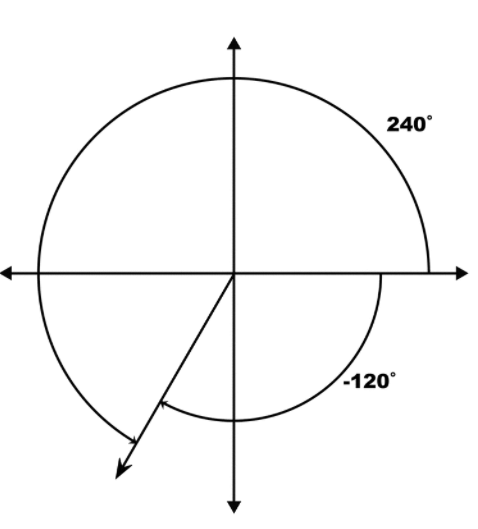
Question 4.
−450°
Answer:

Find one positive angle and one negative angle that are coterminal with the given angle.
Question 5.
80°
Answer:
positive angle = 80 + 360 = 440°
80 – 360 = -280°
Question 6.
230°
Answer:
230 + 360 = 590°
230 – 360 = -130°
Question 7.
740°
Answer:
740 + 360 = 1100°
740 – 360 = 380°
Question 8.
−135°
Answer:
-135 + 360 = -225°
-135 – 360 = 495°
Convert the degree measure to radians or the radian measure to degrees.
Question 9.
135°
Answer:
135° = 135 x \(\frac { π }{ 180° } \)
= \(\frac { 3π }{ 4 } \)
Question 10.
−40°
Answer:
−40° = -40 x \(\frac { π }{ 180° } \)
= \(\frac { -2π }{ 9 } \)
Question 11.
\(\frac{5 \pi}{4}\)
Answer:
\(\frac{5 \pi}{4}\) = \(\frac{5 \pi}{4}\) x \(\frac { 180° }{ π } \)
= 225°
Question 12.
−6.28
Answer:
−6.28 = −6.28 x \(\frac { 180° }{ π } \)
= -359.81°
Question 13.
WHAT IF?
In Example 4, the outfield fence is 220 feet from home plate. Estimate the length of the outfield fence and the area of the field.
Answer:
The length of outfield fence is 140.05 ft
The area of the field is 15406.19 ft²
Explanation:
θ = \(\frac { π }{ 2 } \)
s = 220
Arc lenth s = rθ
220 = r x \(\frac { π }{ 2 } \)
r = 140.05
Area A = 0.5r²θ
A = 0.5 x (140.05)² x \(\frac { π }{ 2 } \)
A = 15406.19
Angles and Radian Measure 9.2 Exercises
Vocabulary and Core Concept Check
Question 1.
COMPLETE THE SENTENCE
An angle is in standard position when its vertex is at the __________ and its __________ lies on the positive x-axis.
Answer:

Question 2.
WRITING
Explain how the sign of an angle measure determines its direction of rotation.
Answer:
If the sign of an angle’s measure is positive, the direction of rotation of its terminal side will be counter clock wise from the positive x-axis.
If the sign of angle’s measure is negative, the direction of rotation of its terminal side will be clockwise from the positive x-axis.
Question 3.
VOCABULARY
In your own words, define a radian.
Answer:
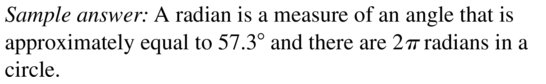
Question 4.
WHICH ONE DOESN’T BELONG?
Which angle does not belong with the other three? Explain your reasoning.

Answer:
450° does not belong with other three. Because it is beyond 360°.
Monitoring Progress and Modeling with Mathematics
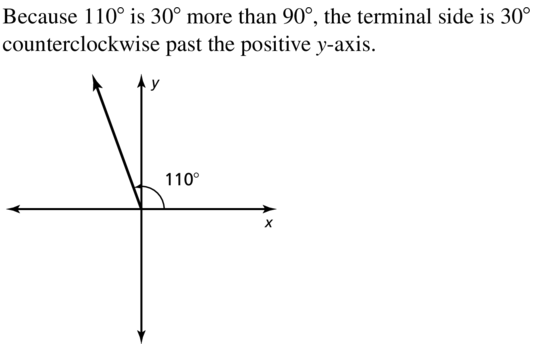
In Exercises 5–8, draw an angle with the given measure in standard position.
Question 5.
110°
Answer:
Question 6.
450°
Answer:
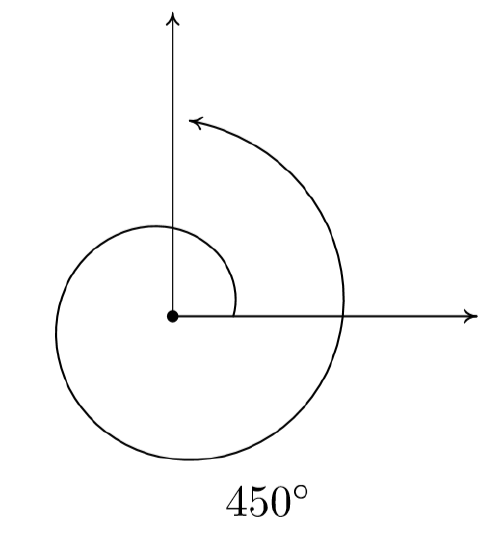
Question 7.
−900°
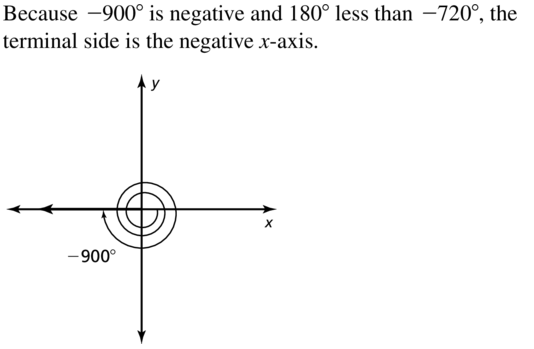
Answer:
Question 8.
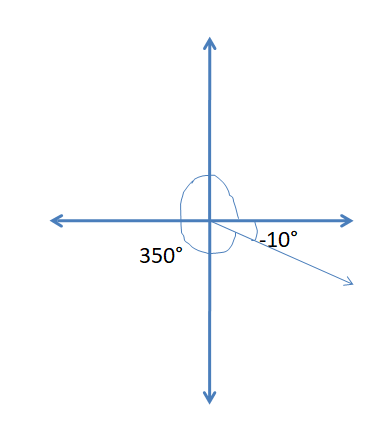
−10°
Answer:
In Exercises 9–12, find one positive angle and one negative angle that are coterminal with the given angle.
Question 9.
70°
Answer:
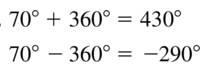
Question 10.
255°
Answer:
225 + 360 = 585°
225 – 360 = -135°
Question 11.
−125°
Answer:
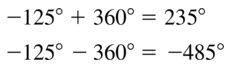
Question 12.
−800°
Answer:
-800 + 360 = -440°
-800 – 360 = -1160°
In Exercises 13–20, convert the degree measure to radians or the radian measure to degrees.
Question 13.
40°
Answer:
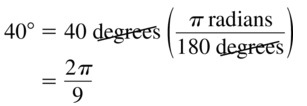
Question 14.
315°
Answer:
315° = 315° x \(\frac { π }{ 180° } \)
= \(\frac { 7π }{ 4 } \)
Question 15.
−260°
Answer:
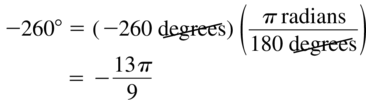
Question 16.
−500°
Answer:
-500° = -500° x \(\frac { π }{ 180° } \)
= \(\frac { 25π }{ 9 } \)
Question 17.
\(\frac{\pi}{9}\)
Answer:
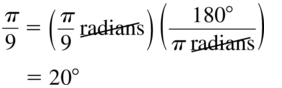
Question 18.
\(\frac{3 \pi}{4}\)
Answer:
\(\frac{3 \pi}{4}\) = \(\frac{3 \pi}{4}\) x \(\frac { 180° }{ π } \)
= 135°
Question 19.
−5
Answer:
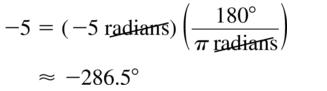
Question 20.
12
Answer:
12 = 12 x \(\frac { 180° }{ π } \)
= 687.54
Question 21.
WRITING
The terminal side of an angle in standard position rotates one-sixth of a revolution counterclockwise from the positive x-axis. Describe how to find the measure of the angle in both degree and radian measures.
Answer:

Question 22.
OPEN-ENDED
Using radian measure, give one positive angle and one negative angle that are coterminal with the angle shown. Justify your answers.

Answer:
315 + 360 = 675°
315 – 360 = -45°
ANALYZING RELATIONSHIPS In Exercises 23–26, match the angle measure with the angle.
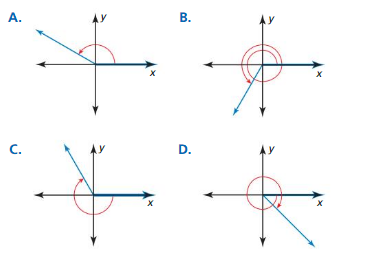
Question 23.
600°
Answer:
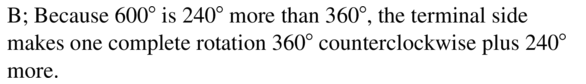
Question 24.
\(-\frac{9 \pi}{4}\)
Answer:
\(-\frac{9 \pi}{4}\) = \(-\frac{9 \pi}{4}\) x \(\frac { 180° }{ π } \) = -405° is 45° more than -360°. The terminal side is 45° anticlockwise past to y-axis.
Question 25.
\(\frac{5 \pi}{6}\)
Answer:

Question 26.
−240°
Answer:
Question 27.
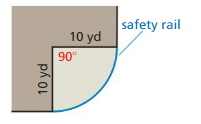
MODELING WITH MATHEMATICS
The observation deck of a building forms a sector with the dimensions shown. Find the length of the safety rail and the area of the deck.
Answer:

Question 28.
MODELING WITH MATHEMATICS
In the men’s shot put event at the 2012 Summer Olympic Games, the length of the winning shot was 21.89 meters. A shot put must land within a sector having a central angle of 34.92° to be considered fair.

a. The officials draw an arc across the fair landing area, marking the farthest throw. Find the length of the arc.
b. All fair throws in the 2012 Olympics landed within a sector bounded by the arc in part (a). What is the area of this sector?
Answer:
Question 29.
ERROR ANALYSIS
Describe and correct the error in converting the degree measure to radians.

Answer:

Question 30.
ERROR ANALYSIS
Describe and correct the error in finding the area of a sector with a radius of 6 centimeters and a central angle of 40°.

Answer:
A = 0.5 x 6² x \(\frac { 40 }{ 360 } \)
A = 2
Question 31.
PROBLEM SOLVING
When a CD player reads information from the outer edge of a CD, the CD spins about 200 revolutions per minute. At that speed, through what angle does a point on the CD spin in oneminute? Give your answer in both degree and radian measures.
Answer:

Question 32.
PROBLEM SOLVING
You work every Saturday from 9:00 A.M. to 5:00 P.M. Draw a diagram that shows the rotation completed by the hour hand of a clock during this time. Find the measure of the angle generated by the hour hand in both degrees and radians. Compare this angle with the angle generated by the minute hand from 9:00 A.M. to 5:00 P.M.
Answer:
The angle that makes hour hand is 240° = \(\frac { 4π }{ 3 } \)
The angle that makes minute hand is 2880° = 16π
Explanation:

1 hour = \(\frac { 360 }{ 12 } \) = 30 degrees
1 hour = \(\frac { 2π }{ 12 } \) = \(\frac { π }{ 6 } \)
Thus, the 8 hours which represents the length of working time, in the radians and degrees are
8 hour = 8 x 30 = 240
8 hour = 8 x \(\frac { π }{ 6 } \) = \(\frac { 4π }{ 3 } \)
By using the part above and by using the hour has 60 minutes the angle generated by the minute hand
8 x 360 = 2880
8 x 2π = 16π
USING TOOLS In Exercises 33–38, use a calculator to evaluate the trigonometric function.
Question 33.
cos \(\frac{4 \pi}{3}\)
Answer:
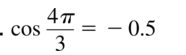
Question 34.
sin \(\frac{7 \pi}{8}\)
Answer:
sin \(\frac{7 \pi}{8}\) = 0.656
Question 35.
csc \(\frac{10 \pi}{11}\)
Answer:
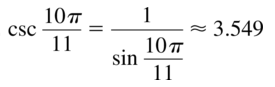
Question 36.
cot (− \(\frac{6 \pi}{5}\))
Answer:
cot (− \(\frac{6 \pi}{5}\)) = 3.43
Question 37.
cot(−14)
Answer:
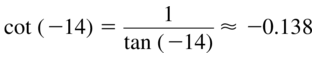
Question 38.
cos 6
Answer:
cos 6 = 0.96
Question 39.
MODELING WITH MATHEMATICS
The rear windshield wiper of a car rotates 120°, as shown. Find the area cleared by the wiper.
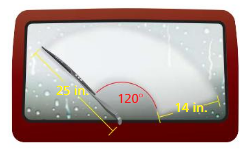
Answer:

Question 40.
MODELING WITH MATHEMATICS
A scientist performed an experiment to study the effects of gravitational force on humans. In order for humans to experience twice Earth’s gravity, they were placed in a centrifuge 58 feet long and spun at a rate of about 15 revolutions per minute.

a. Through how many radians did the people rotate each second?
b. Find the length of the arc through which the people rotated each second.
Answer:
a. The people are rotated each second for \(\frac { π }{ 2 } \) radians
b. The arc length is 45.6 ft.
Explanation:
a. From the given data, the centrifuge has a length of 58 ft and spins at a rate of about 15 revolutions per minute. Thus the radius of the centrifuge will be
r = \(\frac { 58 }{ 2 } \) – 29
Now, since the minute has 60 seconds, then we have
\(\frac { 15 }{ 60 } \) = \(\frac { 1 }{ 4 } \)
which implies that we have \(\frac { 1 }{ 4 } \) revolution per second. Now, since the revolution has 2π radians, humans are rotated per second for the following angle θ
θ = \(\frac { 1 }{ 4 } \) x 2π = \(\frac { π }{ 2 } \)
b. Arc length s = rθ
r = 29 and θ = \(\frac { π }{ 2 } \)
s = 29 x \(\frac { π }{ 2 } \)
= 45.6
Question 41.
REASONING
In astronomy, the terminator is the day-night line on a planet that divides the planet into daytime and nighttime regions. The terminator moves across the surface of a planet as the planet rotates. It takes about 4 hours for Earth’s terminator to move across the continental United States. Through what angle has Earth rotated during this time? Give your answer in both degree and radian measures.
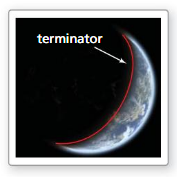
Answer:

Question 42.
HOW DO YOU SEE IT?
Use the graph to find the measure of θ. Explain your reasoning.

Answer:
Question 43.
MODELING WITH MATHEMATICS
A dartboard is divided into 20 sectors. Each sector is worth a point value from 1 to 20 and has shaded regions that double or triple this value. A sector is shown below. Find the areas of the entire sector, the double region, and the triple region.
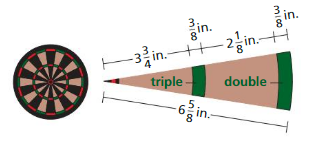
Answer:

Question 44.
THOUGHT PROVOKING
π is an irrational number, which means that it cannot be written as the ratio of two whole numbers. π can, however, be written exactly as a continued fraction, as follows.
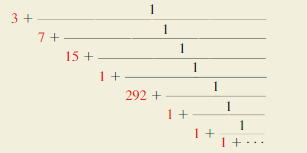
Answer:
Continued fraction converges to π.
Explanation:
Now let’s prove that last continued fraction converges to π = 3.14159
By direct calculation, we get
3 + \(\frac { 1 }{ 7 } \) = 3 + 0.1428 = 3.1428
3 + \(\frac { 1 }{ 7 + 1/15 } \) = 3 + \(\frac { 1 }{ 7 + 0.066 } \) = 3 + 0.141 = 3.141
3 + \(\frac { 1 }{ 7 + 1/15 + 1 } \) = 3 + \(\frac { 1 }{ 7.0625 } \) = 3 + 0.14159
= 3.14159
From the following above, when we continue with the last computation, we can notice that in each row we estimate the number π with greater precision each time. Thus, we can claim that the continued fraction converges to the number π.
Question 45.
MAKING AN ARGUMENT
Your friend claims that when the arc length of a sector equals the radius, the area can be given by A = \(\frac{s^{2}}{2}\). Is your friend correct? Explain.
Answer:
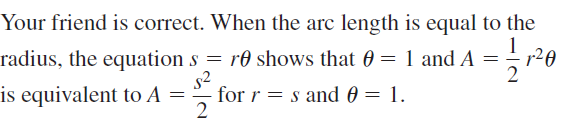
Question 46.
PROBLEM SOLVING
A spiral staircase has 15 steps. Each step is a sector with a radius of 42 inches and a central angle of \(\frac{\pi}{8}\).
a. What is the length of the arc formed by the outer edge of a step?
b. Through what angle would you rotate by climbing the stairs?
c. How many square inches of carpeting would you need to cover the 15 steps?
Answer:
a. Arc length s = 16.49
b. Angle of rotation is \(\frac { 15π }{ 8 } \)
c. Area A = 5195.4
Explanation:
a. Arc length s = rθ
r = 42 and θ = \(\frac { π }{ 8 } \)
s = 42 x \(\frac { π }{ 8 } \) = 16.49
b. A spiral staircase that has 15 steps and in each step has an angle of rotation of \(\frac { π }{ 8 } \). Thus by climbing the stairs we rotatte for angle
15 x \(\frac { π }{ 8 } \) = \(\frac { 15π }{ 8 } \)
c. A = 0.5 x r²θ
A1 = 0.5 x 42θ x \(\frac { π }{ 8 } \) = 346.361
Hence, the area of the 15 stairs will be A = 15 x A1 = 15 x 346.36 = 5195.4
Question 47.
MULTIPLE REPRESENTATIONS
There are 60 minutes in 1 degree of arc, and 60 seconds in 1 minute of arc. The notation 50° 30′ 10″ represents an angle with a measure of 50 degrees, 30 minutes, and 10 seconds.
a. Write the angle measure 70.55° using the notation above.
b. Write the angle measure 110° 45′ 30″ to the nearest hundredth of a degree. Justify your answer.
Answer:
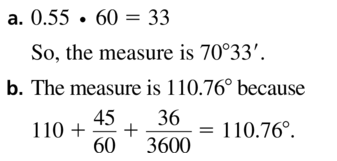
Maintaining Mathematical Proficiency
Find the distance between the two points.
Question 48.
(1, 4), (3, 6)
Answer:
The distance is 2.828
Explanation:
d = √(3 – 1)² + (6 – 4)²
= √4+ 4 = √8
= 2.828
Question 49.
(−7, −13), (10, 8)
Answer:
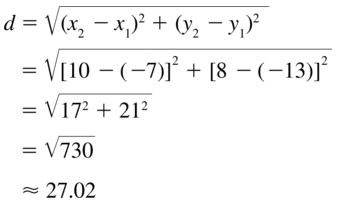
Question 50.
(−3, 9), (−3, 16)
Answer:
The distance is 5
Explanation:
d = √(-3 + 3)² + (16 – 9)²
= √0+ 25 = 5
Question 51.
(2, 12), (8, −5)
Answer:
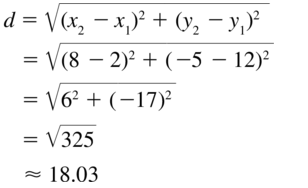
Question 52.
(−14, −22), (−20, −32)
Answer:
The distance is 11.66
Explanation:
d = √(-20 + 14)² + (-32 + 22)²
= √36+ 100 = √136
= 11.66
Question 53.
(4, 16), (−1, 34)
Answer:
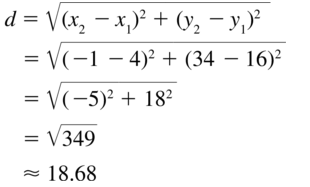
Lesson 9.3 Trigonometric Functions of Any Angle
Essential Question How can you use the unit circle to define the trigonometric functions of any angle?
Let θ be an angle in standard position with (x, y) a point on the terminal side of θ and r = \(\sqrt{x^{2}+y^{2}}\) ≠ 0. The six trigonometric functions of θ are defined as shown.
EXPLORATION 1
Writing Trigonometric Functions
Work with a partner. Find the sine, cosine, and tangent of the angle θ in standard position whose terminal side intersects the unit circle at the point (x, y) shown.
Communicate Your Answer
Question 2.
How can you use the unit circle to define the trigonometric functions of any angle?
Answer:
Question 3.
For which angles are each function undefined? Explain your reasoning.

a. tangent
b. cotangent
c. secant
d. cosecant
Answer:
Monitoring Progress
Evaluate the six trigonometric functions of θ.
Question 1.
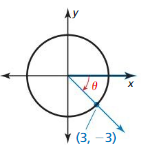
Answer:
sin θ = \(\frac { -1 }{ √2 } \)
cos θ = \(\frac { 1 }{ √2 } \)
tan θ = -1
cot θ = -1
sec θ = √2
csc θ = -√2
Explanation:
r = √3² + (-3)² = 3√2
x = 3, y = -3
sin θ = \(\frac { y }{ r } \) = \(\frac { -3 }{ 3√2 } \)
cos θ = \(\frac { x }{ r } \) = \(\frac { 3 }{ 3√2 } \)
tan θ = \(\frac { y }{ x } \) = \(\frac { -3 }{ 3 } \)
cot θ = \(\frac { x }{ y } \) = \(\frac { 3 }{ -3 } \)
sec θ = \(\frac { r }{ x } \) = \(\frac { 3√2 }{ 3 } \)
csc θ = \(\frac { r }{ y } \) = \(\frac { 3√2 }{ -3 } \)
Question 2.
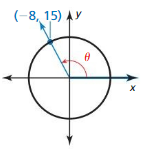
Answer:
sin θ = \(\frac { -1 }{ √2 } \)
cos θ = \(\frac { 1 }{ √2 } \)
tan θ = -1
cot θ = -1
sec θ = √2
csc θ = -√2
Explanation:
r = √3² + (-3)² = 3√2
x = 3, y = -3
sin θ = \(\frac { y }{ r } \) = \(\frac { -3 }{ 3√2 } \)
cos θ = \(\frac { x }{ r } \) = \(\frac { 3 }{ 3√2 } \)
tan θ = \(\frac { y }{ x } \) = \(\frac { -3 }{ 3 } \)
cot θ = \(\frac { x }{ y } \) = \(\frac { 3 }{ -3 } \)
sec θ = \(\frac { r }{ x } \) = \(\frac { 3√2 }{ 3 } \)
csc θ = \(\frac { r }{ y } \) = \(\frac { 3√2 }{ -3 } \)
Question 3.
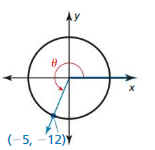
Answer:
sin θ = \(\frac { -12 }{ 13 } \)
cos θ = \(\frac { -5 }{ 13 } \)
tan θ = \(\frac { 12 }{ 5 } \)
cot θ = \(\frac { 5 }{ 12 } \)
sec θ = \(\frac { -13 }{ 5 } \)
csc θ = \(\frac { -13 }{ 12 } \)
Explanation:
r = √(-5)² + (-12)² = 13
x = -5, y = -12
sin θ = \(\frac { y }{ r } \) = \(\frac { -12 }{ 13 } \)
cos θ = \(\frac { x }{ r } \) = \(\frac { -5 }{ 13 } \)
tan θ = \(\frac { y }{ x } \) = \(\frac { 12 }{ 5 } \)
cot θ = \(\frac { x }{ y } \) = \(\frac { 5 }{ 12 } \)
sec θ = \(\frac { r }{ x } \) = \(\frac { -13 }{ 5 } \)
csc θ = \(\frac { r }{ y } \) = \(\frac { -13}{ 12 } \)
Question 4.
Use the unit circle to evaluate the six trigonometric functions of θ = 180º.
Answer:
sin θ = 0
cos θ = -1
tan θ = 0
cot θ = undefined
sec θ = -1
csc θ = undefined
Explanation:
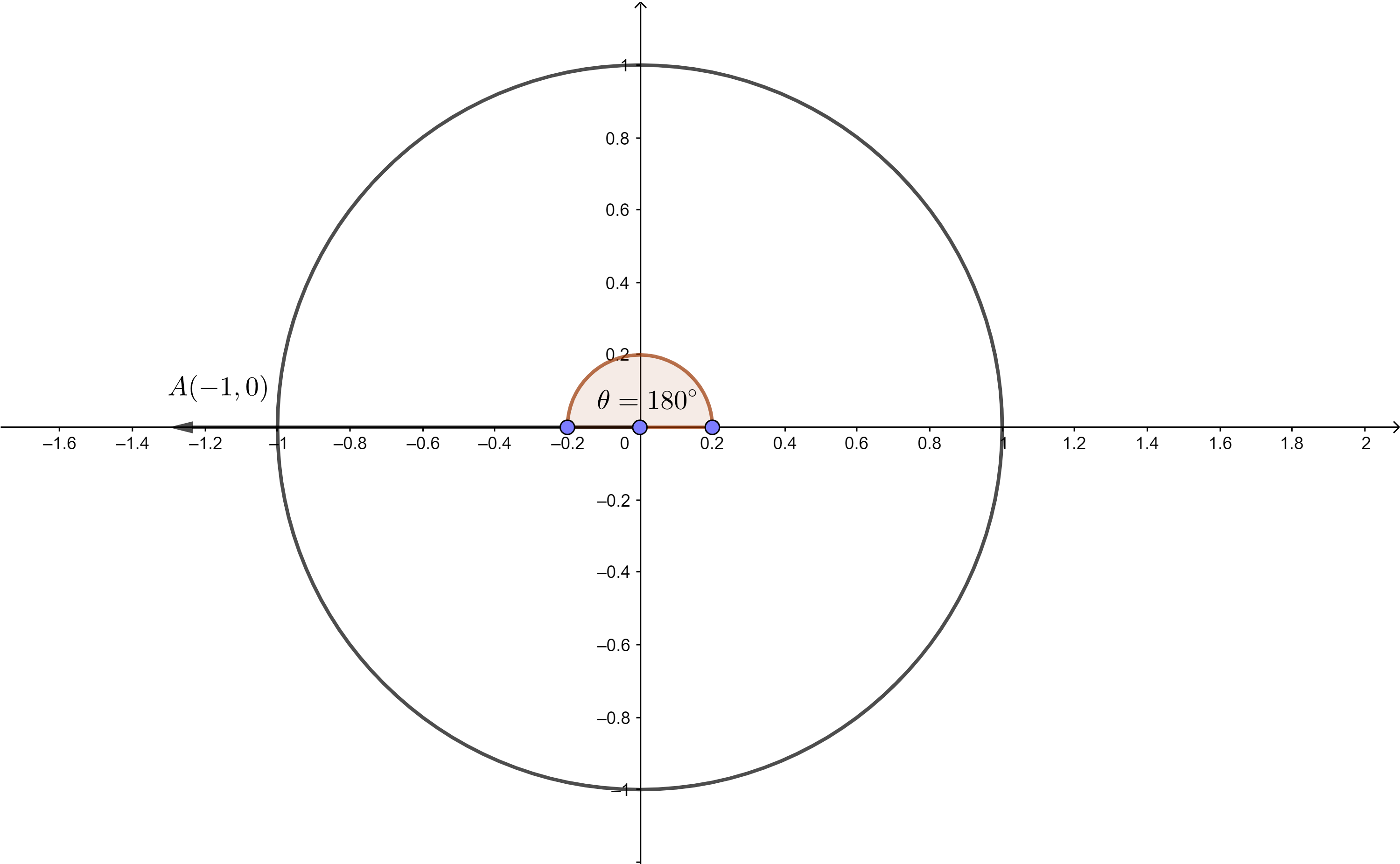
r = 1
x = -1, y = 0
sin θ = \(\frac { y }{ r } \) = \(\frac { 0 }{ 1 } \) = 0
cos θ = \(\frac { x }{ r } \) = \(\frac { -1 }{ 1 } \) = -1
tan θ = \(\frac { y }{ x } \) = \(\frac { 0 }{ -1 } \) = 0
cot θ = \(\frac { x }{ y } \) = \(\frac { -1 }{ 0 } \) = undefined
sec θ = \(\frac { r }{ x } \) = \(\frac { 1 }{ -1 } \) = -1
csc θ = \(\frac { r }{ y } \) = \(\frac { 1}{ 0 } \) = undefined
Sketch the angle. Then find its reference angle.
Question 5.
210°
Answer:
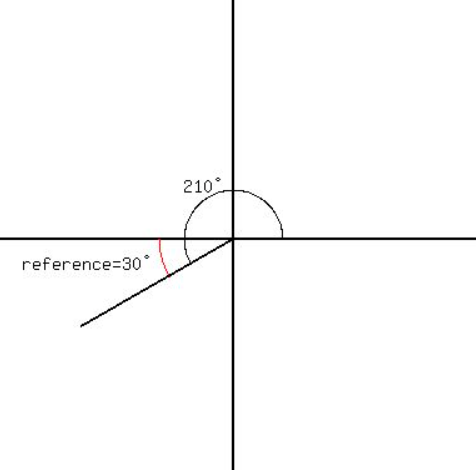
Reference angle = 30°
Question 6.
−260°
Answer:
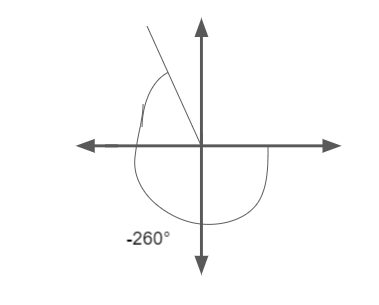
Reference angle = 10°
Question 7.
\(\frac{-7 \pi}{9}\)
Answer:
\(\frac{-7 \pi}{9}\) = \(\frac{-7 \pi}{9}\) x \(\frac { 180 }{ π } \)
= -140°
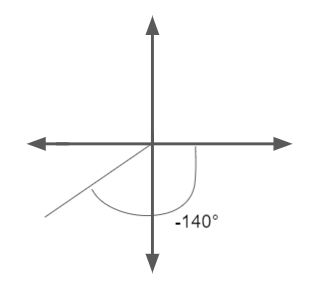
Reference angle = 40°
Question 8.
\(\frac{15 \pi}{4}\)
Answer:
\(\frac{15 \pi}{4}\) = \(\frac{15 \pi}{4}\) x \(\frac { 180 }{ π } \)
= 675°
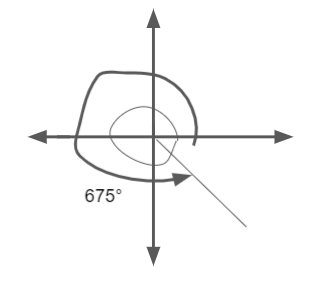
Reference angle = 45°
Evaluate the function without using a calculator.
Question 9.
cos(−210º)
Answer:
cos(−210º) = –\(\frac { √3 }{ 2 } \)
Explanation:
cos(−210º) = cos(210º)
cos(180º + θ) = – cosθ
cos(180º + 30º) = – cos 30º
= –\(\frac { √3 }{ 2 } \)
Question 10.
sec \(\frac{11 \pi}{4}\)
Answer:
sec \(\frac{11 \pi}{4}\) = -√2
Explanation:
sec \(\frac{11 \pi}{4}\) = sec \(\frac{3 \pi}{4}\)
= – sec \(\frac{\pi}{4}\) = -√2
Question 11.
Use the model given in Example 5 to estimate the horizontal distance traveled by a track and field long jumper who jumps at an angle of 20° and with an initial speed of 27 feet per second.
Answer:
The horizontal distance traveled by a track and field longer jumper is 14.62 sq ft
Explanation:
d = \(\frac { v² }{ 32 } \) sin 2θ
θ = 20°, v = 27
d = \(\frac { 27² }{ 32 } \) sin 2(20°)
= 22.78 x sin 40°
= 14.62
Trigonometric Functions of Any Angle 9.3 Exercises
Vocabulary and Core Concept Check
Question 1.
COMPLETE THE SENTENCE
A(n) ___________ is an angle in standard position whose terminal side lies on an axis.
Answer:
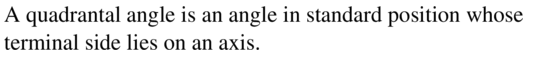
Question 2.
WRITING
Given an angle θ in standard position with its terminal side in Quadrant III, explain how you can use a reference angle to find cos θ.
Answer:
cos θ = – cos θ’
Monitoring Progress and Modeling with Mathematics
In Exercises 3–8, evaluate the six trigonometric functions of θ.
Question 3.
Answer:

Question 4.
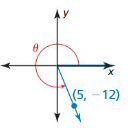
Answer:
sin θ = \(\frac { -12 }{ 13 } \)
cos θ = \(\frac { 5 }{ 13 } \)
tan θ = \(\frac { -12 }{ 5 } \)
cot θ = \(\frac { -5 }{ 12 } \)
sec θ = \(\frac { 13 }{ 5 } \)
csc θ = \(\frac { -13 }{ 12 } \)
Explanation:
r = √(5)² + (-12)² = 13
x = 5, y = -12
sin θ = \(\frac { y }{ r } \) = \(\frac { -12 }{ 13 } \)
cos θ = \(\frac { x }{ r } \) = \(\frac { 5 }{ 13 } \)
tan θ = \(\frac { y }{ x } \) = \(\frac { -12 }{ 5 } \)
cot θ = \(\frac { x }{ y } \) = \(\frac { 5 }{ -12 } \)
sec θ = \(\frac { r }{ x } \) = \(\frac { 13 }{ 5 } \)
csc θ = \(\frac { r }{ y } \) = \(\frac { -13}{ 12 } \)
Question 5.
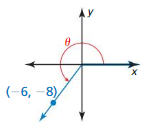
Answer:

Question 6.

Answer:
sin θ = \(\frac { 1 }{ √10 } \)
cos θ = \(\frac { 3 }{ √10 } \)
tan θ = \(\frac { 1 }{ 3 } \)
cot θ = 3
sec θ = \(\frac { √10 }{ 3 } \)
csc θ = √10
Explanation:
r = √3² + 1² = √10
x = 3, y = 1
sin θ = \(\frac { y }{ r } \) = \(\frac { 1 }{ √10 } \)
cos θ = \(\frac { x }{ r } \) = \(\frac { 3 }{ √10 } \)
tan θ = \(\frac { y }{ x } \) = \(\frac { 1 }{ 3 } \)
cot θ = \(\frac { x }{ y } \) = \(\frac { 3 }{ 1 } \)
sec θ = \(\frac { r }{ x } \) = \(\frac { √10 }{ 3 } \)
csc θ = \(\frac { r }{ y } \) = \(\frac { √10}{ 1 } \)
Question 7.
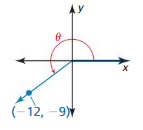
Answer:

Question 8.
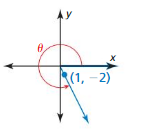
Answer:
sin θ = \(\frac { -2 }{ √5 } \)
cos θ = \(\frac { 1 }{ √5 } \)
tan θ =-2
cot θ = \(\frac { -1 }{ 2 } \)
sec θ = √5
csc θ = \(\frac { -√5 }{ 2 } \)
Explanation:
r = √(1)² + (-2)² = √5
x = 1, y = -2
sin θ = \(\frac { y }{ r } \) = \(\frac { -2 }{ √5 } \)
cos θ = \(\frac { x }{ r } \) = \(\frac { 1 }{√5 } \)
tan θ = \(\frac { y }{ x } \) = \(\frac { -2 }{ 1 } \)
cot θ = \(\frac { x }{ y } \) = \(\frac { 1 }{ -2 } \)
sec θ = \(\frac { r }{ x } \) = \(\frac { √5 }{ 1 } \)
csc θ = \(\frac { r }{ y } \) = \(\frac { -√5 }{ 2 } \)
In Exercises 9–14, use the unit circle to evaluate the six trigonometric functions of θ.
Question 9.
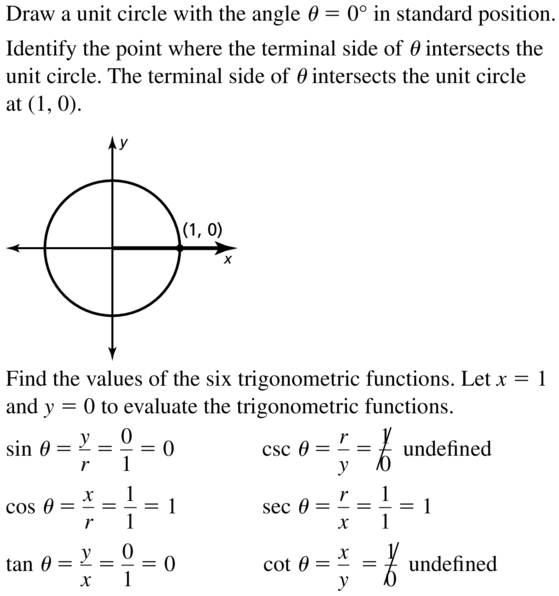
θ = 0°
Answer:
Question 10.
θ = 540°
Answer:
sin θ = 0
cos θ = -1
tan θ = 0
cot θ = undefined
sec θ = -1
csc θ = undefined
Explanation:
θ = 540° = 180°
The point A = (-1, 0)
x = -1, y = 0 and r = 1
sin θ = \(\frac { y }{ r } \) = \(\frac { 0 }{ 1 } \)
cos θ = \(\frac { x }{ r } \) = \(\frac { -1 }{1 } \)
tan θ = \(\frac { y }{ x } \) = \(\frac { 0 }{ -1 } \)
cot θ = \(\frac { x }{ y } \) = \(\frac { -1 }{ 0 } \)
sec θ = \(\frac { r }{ x } \) = \(\frac { 1 }{ -1 } \)
csc θ = \(\frac { r }{ y } \) = \(\frac { 1 }{ 0 } \)
Question 11.
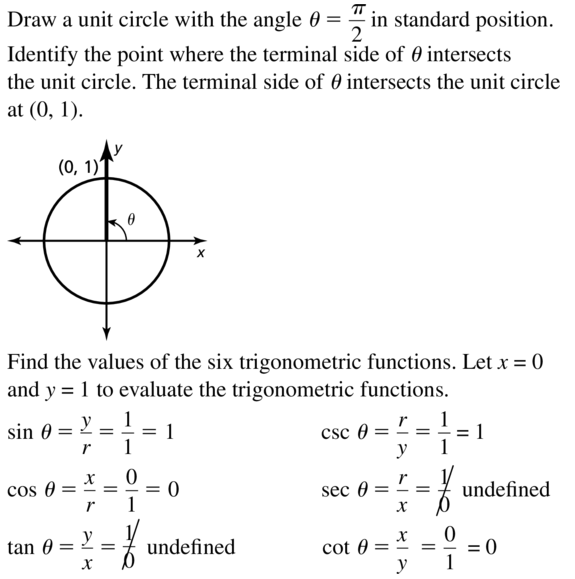
θ = \(\frac{\pi}{2}\)
Answer:
Question 12.
θ = \(\frac{7 \pi}{2}\)
Answer:
sin θ = -1
cos θ = 0
tan θ = undefined
cot θ = 0
sec θ = undefined
csc θ = -1
Explanation:
θ = \(\frac{7 \pi}{2}\)
The point A = (0, -1)
x = 0, y = -1 and r = 1
sin θ = \(\frac { y }{ r } \) = \(\frac { -1 }{ 1 } \)
cos θ = \(\frac { x }{ r } \) = \(\frac { 0 }{1 } \)
tan θ = \(\frac { y }{ x } \) = \(\frac { -1 }{ 0 } \)
cot θ = \(\frac { x }{ y } \) = \(\frac { 0 }{ -1 } \)
sec θ = \(\frac { r }{ x } \) = \(\frac { 1 }{ 0 } \)
csc θ = \(\frac { r }{ y } \) = \(\frac { 1 }{ -1 } \)
Question 13.
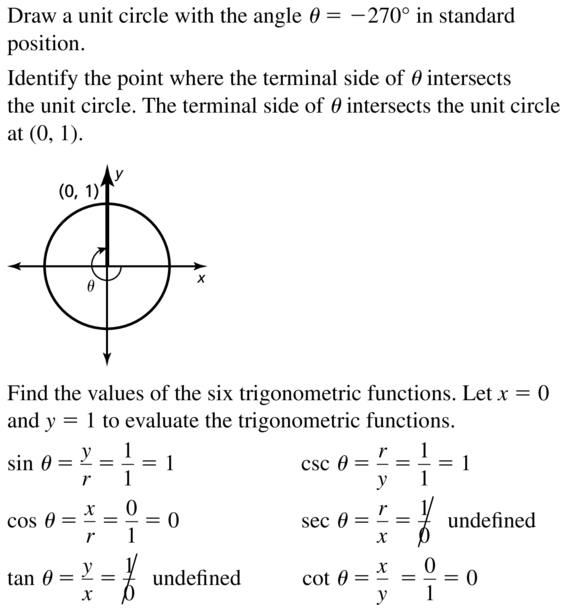
θ = −270°
Answer:
Question 14.
θ = −2π
Answer:
sin θ = 0
cos θ = 1
tan θ = 0
cot θ = undefined
sec θ = 1
csc θ = undefined
Explanation:
θ = −2π
The point A = (1, 0)
x = 1, y = 0 and r = 1
sin θ = \(\frac { y }{ r } \) = \(\frac { 0 }{ 1 } \)
cos θ = \(\frac { x }{ r } \) = \(\frac { 1 }{1 } \)
tan θ = \(\frac { y }{ x } \) = \(\frac { 0 }{ 1 } \)
cot θ = \(\frac { x }{ y } \) = \(\frac { 1 }{ 0 } \)
sec θ = \(\frac { r }{ x } \) = \(\frac { 1 }{ 1 } \)
csc θ = \(\frac { r }{ y } \) = \(\frac { 1 }{ 0 } \)
In Exercises 15–22, sketch the angle. Then find its reference angle.
Question 15.
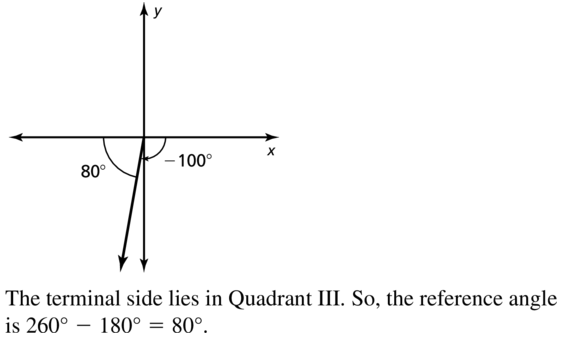
−100°
Answer:
Question 16.
150°
Answer:
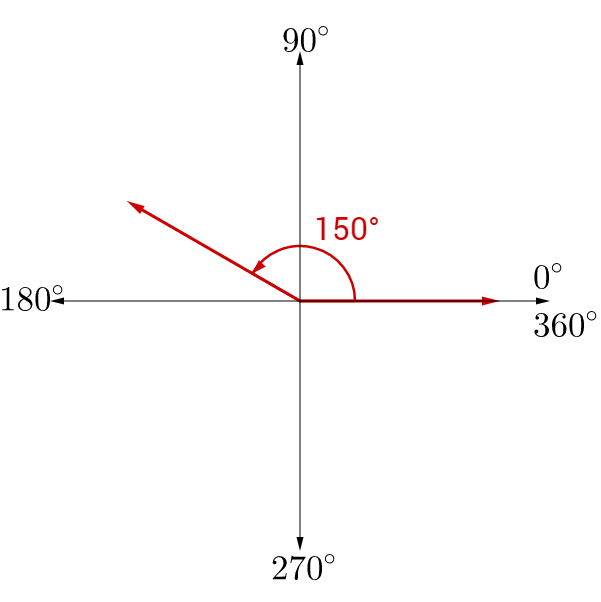
The teriminal side lies in Q2. So the reference angle is 180 – 150 = 30°
Question 17.
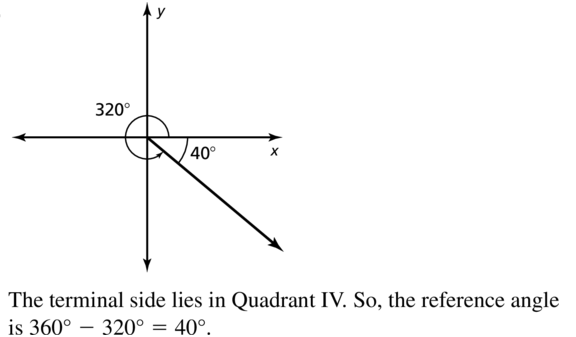
320°
Answer:
Question 18.
−370°
Answer:
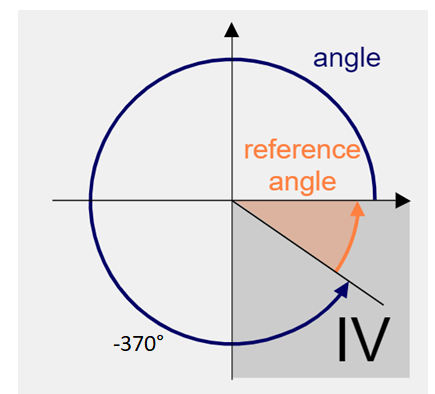
Reference angle = 10°
Question 19.
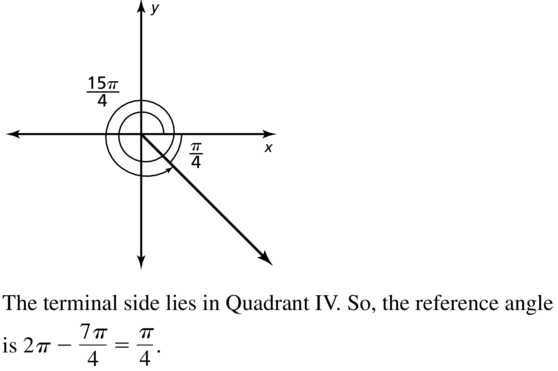
\(\frac{15 \pi}{4}\)
Answer:
Question 20.
\(\frac{8 \pi}{3}\)
Answer:
Question 21.
−\(\frac{5 \pi}{6}\)
Answer:
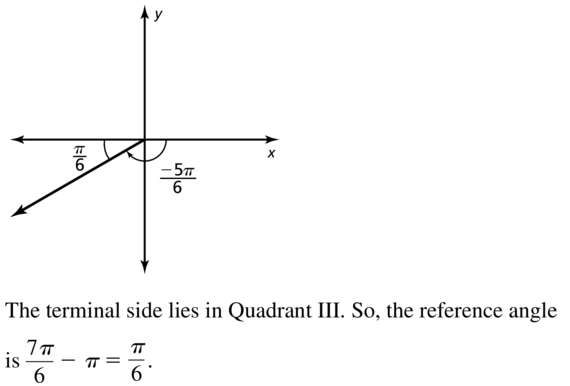
Question 22.
−\(\frac{13 \pi}{6}\)
Answer:
Question 23.
ERROR ANALYSIS
Let (−3, 2) be a point on the terminal side of an angle θ in standard position. Describe and correct the error in finding tan θ.

Answer:
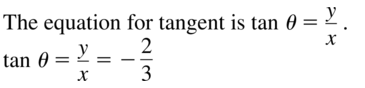
Question 24.
ERROR ANALYSIS
Describe and correct the error in finding a reference angle θ′ for θ = 650°.
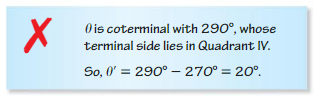
Answer:
In Exercises 25–32, evaluate the function without using a calculator.
Question 25.
sec 135°
Answer:
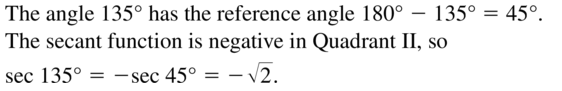
Question 26.
tan 240°
Answer:
The angle 240° has the refence angle 270 – 240 = 30°. The tan function is positive in QIII.
So, tan 240° = tan 30° = 0.577
Question 27.
sin(−150°)
Answer:
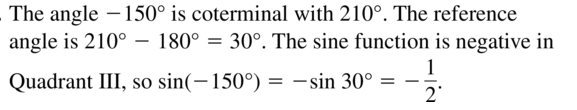
Question 28.
csc(−420°)
Answer:
The angle −420° is coterminal with -60°.
The cosec(-420°) = cosec(-60°) = -1.154
Question 29.
tan (−\(\frac{3 \pi}{4}\))
Answer:

Question 30.
cot (\(\frac{-8 \pi}{3}\))
Answer:
The angle \(\frac{-8 \pi}{3}\) is coterminal with \(\frac{4 \pi}{3}\). The reference angle is \(\frac{4 \pi}{3}\) – π = π/4
Cot function is positive in QIII. So, cot (\(\frac{-8 \pi}{3}\)) = cot (\(\frac{ \pi}{4}\)) = 1
Question 31.
cos \(\frac{7 \pi}{4}\)
Answer:
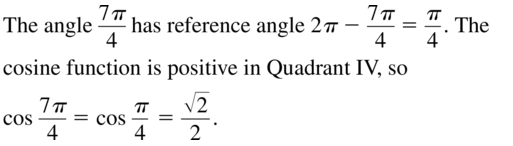
Question 32.
sec \(\frac{11 \pi}{6}\)
Answer:
In Exercises 33–36, use the model for horizontal distance given in Example 5.
Question 33.
You kick a football at an angle of 60° with an initial speed of 49 feet per second. Estimate the horizontal distance traveled by the football.
Answer:

Question 34.
The “frogbot” is a robot designed for exploring rough terrain on other planets. It can jump at a 45° angle with an initial speed of 14 feet per second. Estimate the horizontal distance the frogbot can jump on Earth.

Answer:
Question 35.
At what speed must the in-line skater launch himself off the ramp in order to land on the other side of the ramp?

Answer:

Question 36.
To win a javelin throwing competition, your last throw must travel a horizontal distance of at least 100 feet. You release the javelin at a 40° angle with an initial speed of 71 feet per second. Do you win the competition? Justify your answer.
Answer:
Question 37.
MODELING WITH MATHEMATICS
A rock climber is using a rock climbing treadmill that is 10 feet long. The climber begins by lying horizontally on the treadmill, which is then rotated about its midpoint by 110° so that the rock climber is climbing toward the top. If the midpoint of the treadmill is 6 feet above the ground, how high above the ground is the top of the treadmill?
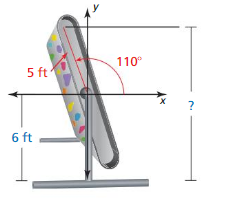
Answer:

Question 38.
REASONING
A Ferris wheel has a radius of 75 feet. You board a car at the bottom of the Ferris wheel, which is 10 feet above the ground, and rotate 255°counterclockwise before the ride temporarily stops. How high above the ground are you when the ride stops? If the radius of the Ferris wheel is doubled, is your height above the ground doubled? Explain your reasoning.
Answer:
104.41 ft
Explanation:
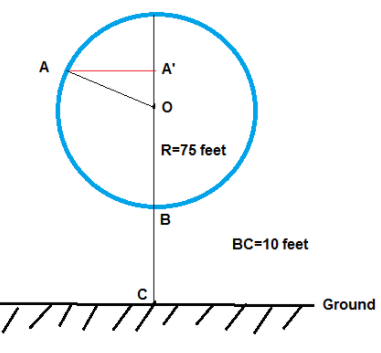
AC’ = A’O + OB + BC = A’O + 75 + 10 = A’O + 85
So we need to calculate A’O
sin (A’AO) = \(\frac { A’O }{ AO } \) = \(\frac { A’O }{ R } \)
A’O = Rsin(A’AO)
∠A’AO = 360 – 225 – 90 = 15
A’O = Rsin(A’AO) = 75 sin(15) = 19.41
A’C = A’O + 85
= 19.41 + 85 = 104.41
If the radius doubled, then
A’C = A’O + OB + BC
= Rsin(A’AO) + R + Bc = 2 x 75 sin(15) + 2 x 75 + 10 = 198.82
So we conclude the height won’t double.
Question 39.
DRAWING CONCLUSIONS
A sprinkler at ground level is used to water a garden. The water leaving the sprinkler has an initial speed of 25 feet per second.
a. Use the model for horizontal distance given in Example 5 to complete the table.

b. Which value of θ appears to maximize the horizontal distance traveled by the water? Use the model for horizontal distance and the unit circle to explain why your answer makes sense.
c. Compare the horizontal distance traveled by the water when θ = (45 − k)° with the distance when θ = (45 + k)°, for 0 < k < 45.
Answer:
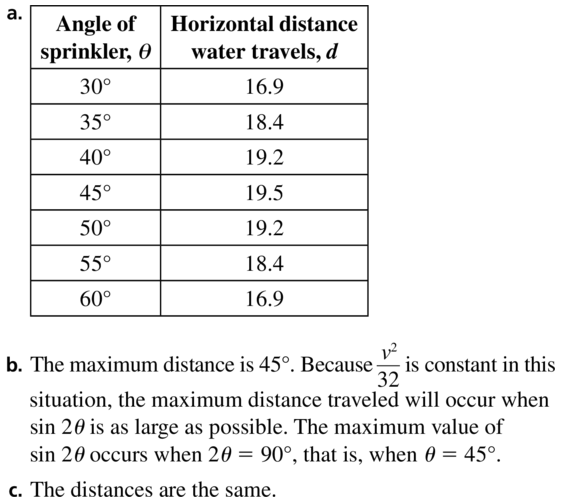
Question 40.
MODELING WITH MATHEMATICS
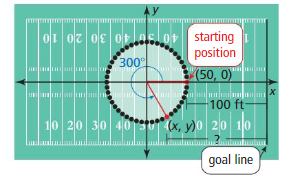
Your school’s marching band is performing at halftime during a football game. In the last formation, the band members form a circle 100 feet wide in the center of the field. You start at a point on the circle 100 feet from the goal line, march 300° around the circle, and then walk toward the goal line to exit the field. How far from the goal line are you at the point where you leave the circle?
Answer:
Question 41.
ANALYZING RELATIONSHIPS
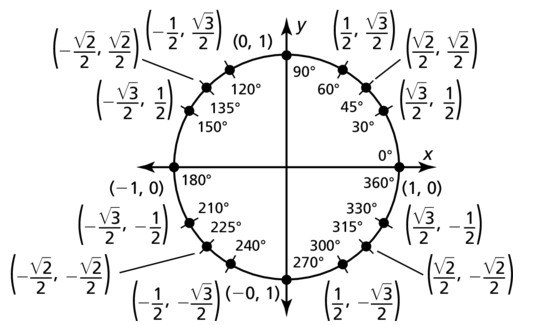
Use symmetry and the given information to label the coordinates of the other points corresponding to special angles on the unit circle.
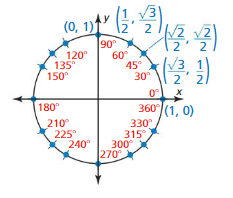
Answer:
Question 42.
THOUGHT PROVOKING
Use the interactive unit circle tool at BigIdeasMath.com to describe all values of θ for each situation.
a. sin θ > 0, cos θ < 0, and tan θ > 0
b. sin θ > 0, cos θ < 0, and tan θ < 0
Answer:
a) Not possible
b) The angle θ must be from the second quadrant, 90° < θ < 180°
Explanation:
a) If we consider that funtion sin θ is positive and the funtion cos θ is negative implies that the angle θ belongs to the second quadrant. Thus, in the second quadrant, tan θ is negative which implies that the following situation
sin θ > 0, cos θ < 0, tan θ > 0 is not possible
b. Now by using the part a), in the second quadrant, for θ belongs to (90, 180) the functions are
sin θ > 0, cos θ < 0, tan θ < 0
From the above, the angle θ must stand 90 < θ < 180
Question 43.
CRITICAL THINKING
Write tan θ as the ratio of two other trigonometric functions. Use this ratio to explain why tan 90° is undefined but cot 90° = 0.
Answer:

Question 44.
HOW DO YOU SEE IT?
Determine whether each of the six trigonometric functions of θ is positive, negative, or zero. Explain your reasoning.
Answer:
Question 45.
USING STRUCTURE
A line with slope m passes through the origin. An angle θ in standard position has a terminal side that coincides with the line. Use a trigonometric function to relate the slope of the line to the angle.
Answer:

Question 46.
MAKING AN ARGUMENT
Your friend claims that the only solution to the trigonometric equation tan θ = \(\sqrt{3}\) is θ= 60°. Is your friend correct? Explain your reasoning.
Answer:
Friend is not correct.
Explanation:
No, he is not correct. Any angle which is coterminal with the angle θ = 60° is the solution for the equation.
Question 47.
PROBLEM SOLVING
When two atoms in a molecule are bonded to a common atom, chemists are interested in both the bond angle and the lengths of the bonds. An ozone molecule is made up of two oxygen atoms bonded to a third oxygen atom, as shown.
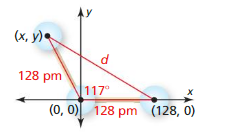
a. In the diagram, coordinates are given in picometers (pm). (Note: 1 pm = 10−12 m) Find the coordinates (x, y) of the center of the oxygen atom in Quadrant II.
b. Find the distance d (in picometers) between the centers of the two unbonded oxygen atoms.
Answer:

Question 48.
MATHEMATICAL CONNECTIONS
The latitude of a point on Earth is the degree measure of the shortest arc from that point to the equator. For example, the latitude of point P in the diagram equals the degree measure of arc PE. At what latitude θ is the circumference of the circle of latitude at P half the distance around the equator?
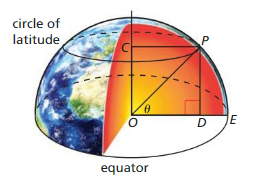
Answer:
Maintaining Mathematical Proficiency
Find all real zeros of the polynomial function.
Question 49.
f (x) = x4 + 2x3 + x2 + 8x − 12
Answer:

Question 50.
f(x) = x5 + 4x4 − 14x3 − 14x2 − 15x− 18
Answer:
Graph the function.
Question 51.
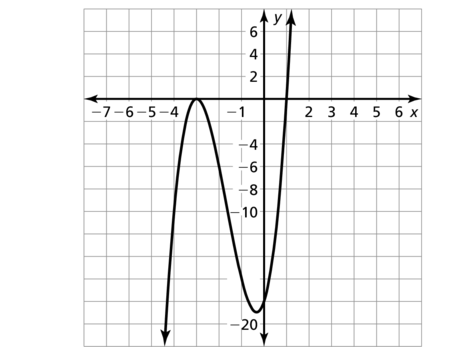
f(x) = 2(x+ 3)2 (x − 1)
Answer:

Question 52.
f(x) = \(\frac{1}{2}\) (x − 4)(x + 5)(x + 9)
Answer:
Question 53.
f(x) = x2(x + 1)3 (x − 2)
Answer:

Lesson 9.4 Graphing Sine and Cosine Functions
Essential Question What are the characteristics of the graphs of the sine and cosine functions?
EXPLORATION 1
Graphing the Sine FunctionWork with a partner.
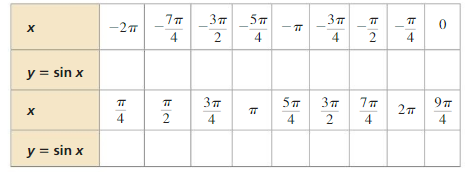
a. Complete the table for y= sin x, where x is an angle measure in radians.
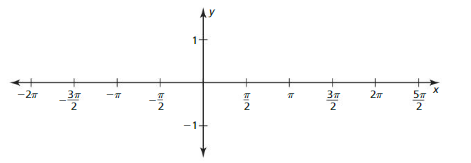
b. Plot the points (x, y) from part (a). Draw a smooth curve through the points to sketch the graph of y = sin x.
c. Use the graph to identify the x-intercepts, the x-values where the local maximums and minimums occur, and the intervals for which the function is increasing or decreasing over −2π ≤ x ≤ 2π. Is the sine function even, odd, or neither?
EXPLORATION 2
Graphing the Cosine Function
Work with a partner.
a. Complete a table for y= cos x using the same values of x as those used in Exploration 1.
b. Plot the points (x, y) from part (a) and sketch the graph of y= cos x.
c. Use the graph to identify the x-intercepts, the x-values where the local maximums and minimums occur, and the intervals for which the function is increasing or decreasing over −2π ≤ x ≤ 2π. Is the cosine function even, odd, or neither?
Communicate Your Answer
Question 3.
What are the characteristics of the graphs of the sine and cosine functions?
Answer:
Question 4.
Describe the end behavior of the graph of y = sin x

Answer:
Monitoring Progress
Identify the amplitude and period of the function. Then graph the function and describe the graph of g as a transformation of the graph of its parent function.
Question 1.
g(x) = \(\frac{1}{4}\)sin x
Answer:
Amplitude = \(\frac{1}{4}\)
Period = 2π
Explanation:
The function is in the form of y = a sinbx
So, a = \(\frac{1}{4}\), b = 1
Ampliute = |a| = | \(\frac{1}{4}\)| = \(\frac{1}{4}\)
Period = \(\frac{2π}{b}\) = 2π

Question 2.
g(x) = cos 2x
Answer:
Amplitude = 1
Period = π
Explanation:
The function is in the form of y = a cosbx
So, a = 1, b = 2
Ampliute = |a| = 1
Period = \(\frac{2π}{b}\) = \(\frac{2π}{2}\) = π
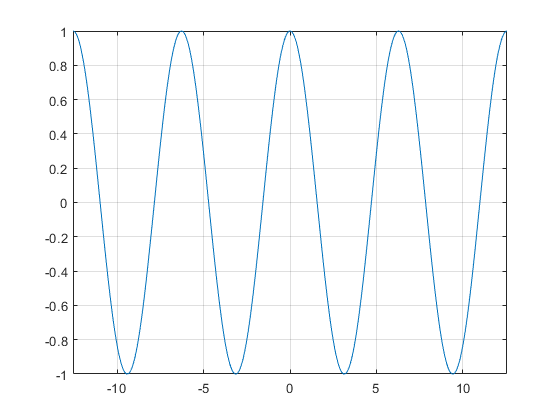
Question 3.
g(x) = 2 sin πx
Answer:
Amplitude = 2
Period = 2
Explanation:
The function is in the form of y = a sinbx
So, a = 2, b = π
Ampliute = |a| = 2
Period = \(\frac{2π}{b}\) = \(\frac{2π}{π}\) = 2

Question 4.
g(x) = \(\frac{1}{3}\) cos \(\frac{1}{2}\)x
Answer:
Amplitude = \(\frac{1}{3}\)
Period = 4π
Explanation:
The function is in the form of y = a cosbx
So, a = \(\frac{1}{3}\), b = \(\frac{1}{2}\)
Ampliute = |a| = \(\frac{1}{3}\)
Period = \(\frac{2π}{b}\) = \(\frac{2π}{[latex]\frac{1}{2}\)}[/latex] = 4π

Graph the function.
Question 5.
g(x) = cos x+ 4
Answer:
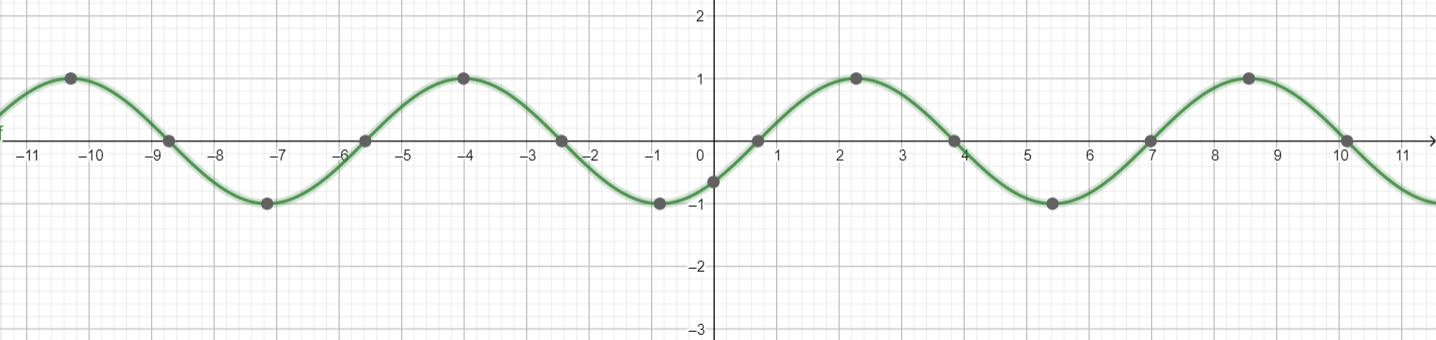
Explanation:
amplitude = 1
Question 6.
g(x) = \(\frac{1}{2}\)sin (x − \(\left.\frac{\pi}{2}\right\))
Answer:

Explanation:
amplitude = 1/2
Question 7.
g(x) = sin(x + π) − 1
Answer:

Explanation:
amplitude = -1
Period = 2π
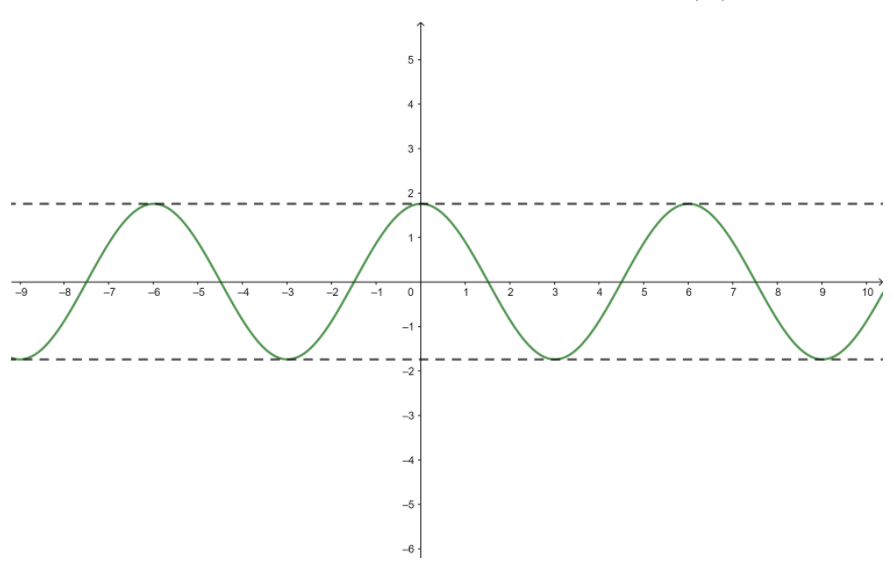
Midline y = -1
Horizontal shift = π
Vertical shift = -1
Midline intercepts (0 – π, -1) = (-π, -1)
Maximum = (\(\frac { 1 }{ 4 } \) . \(\frac { 2π }{ b } \) – π, k + a) = (\(\frac { -π }{ 2 } \), 0)
Minimum = (\(\frac { 3 }{ 4 } \) . \(\frac { 2π }{ b } \) = (\(\frac { 3π }{ 2 } \), -2)
Graph the function.
Question 8.
g(x) = −cos (x + \(\left.\frac{\pi}{2}\right\))
Answer:

Question 9.
g(x) = −3 sin \(\frac{1}{2}\)x + 2
Answer:
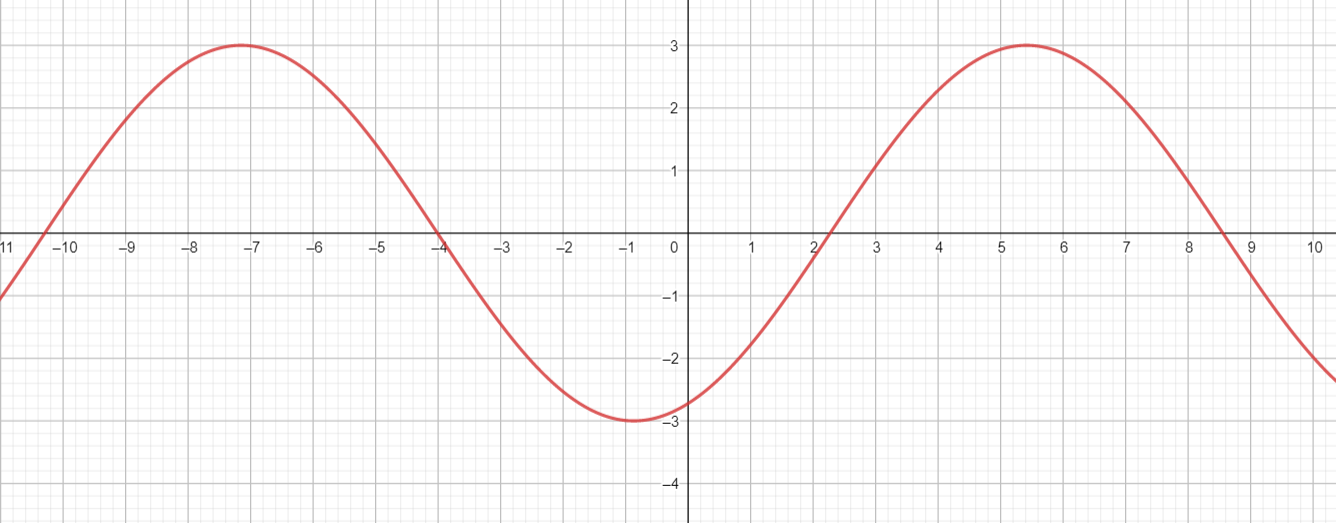
Explanation:
Given that,
g(x) = −3 sin \(\frac{1}{2}\)x + 2
a = -3, b = \(\frac { 1 }{ 2 } \), h = 0, k = 2
Amplitude = |a| = |-3| = 3
Period = \(\frac { 2π }{ b } \) = \(\frac { 2π }{ 0.5 } \) = 4π
midline y = 2
vertical shift = 2
horizontal shift = 0
midline intercepts (\(\frac { π }{ b } \), k) = (\(\frac { π }{ 2 . 0.5 } \), 2 + 3) = (π, 5)
Maximum = (\(\frac { 1 }{ 4 } \) . \(\frac { 2π }{ b } \), k + a) = (\(\frac { π }{ 2 . 0.5 } \), 2 + 3) = (π, 5)
Minimum = (\(\frac { 3 }{ 4 } \) . \(\frac { 2π }{ b } \), k – a) = (\(\frac { 3π }{ 2 . 0.5 } [/latex } , 2 – 3) = (3π, -1)
Question 10.
g(x) = −2 cos 4x − 1
Answer:
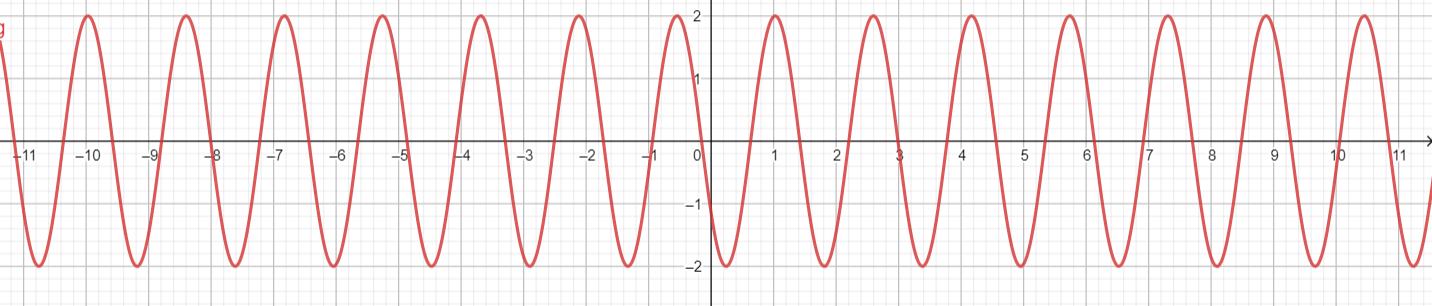
Explanation:
Given that,
g(x) = −2 cos 4x − 1
a = -2, b = 4, h = 0, k = -1
Amplitude = |a| = |-2| = 2
Period = [latex]\frac { 2π }{ b } \) = \(\frac { 2π }{ 4 } \) = \(\frac { π }{ 2 } \)
midline y = -1
vertical shift = -1
horizontal shift = 0
x intercepts = (\(\frac { π }{ 2b } \), k) = (\(\frac { π }{ 2 . 4 } \), -1) = (\(\frac { π }{ 8 } \), -1)
Maximum = (\(\frac { 2π }{ b } \), k + a) = (\(\frac { 2π }{ 4 } \), -1 + 2) = (\(\frac { π }{ 2 } \), 1)
Minimum = (\(\frac { 1 }{ 2 } \) . \(\frac { 2π }{ b } \), k – a) = (\(\frac { π }{ 4 } \), -3)
Graphing Sine and Cosine Functions 9.4 Exercises
Vocabulary and Core Concept Check
Question 1.
COMPLETE THE SENTENCE
The shortest repeating portion of the graph of a periodic function is called a(n) _________.
Answer:

Question 2.
WRITING
Compare the amplitudes and periods of the functions y = \(\frac{1}{2}\)cos x and y = 3 cos 2x.
Answer:
amplitude of y = \(\frac{1}{2}\)cos x is \(\frac{1}{2}\)
Amplitude of y = 3 cos 2x is 3
period of y = \(\frac{1}{2}\)cos x is 2π
Period of y = 3 cos 2x is π
Question 3.
VOCABULARY
What is a phase shift? Give an example of a sine function that has a phase shift.
Answer:
Question 4.
VOCABULARY
What is the midline of the graph of the function y = 2 sin 3(x + 1) − 2?
Answer:
x-axis is the midline of the graph of the function y = 2 sin 3(x + 1) − 2
Monitoring Progress and Modeling with Mathematics
USING STRUCTURE In Exercises 5–8, determine whether the graph represents a periodic function. If so, identify the period.
Question 5.
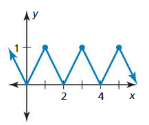
Answer:
![]()
Question 6.
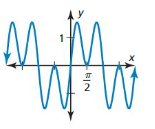
Answer:
The function is a periodic function with a period of \(\frac { π }{ 2 } \)
Question 7.
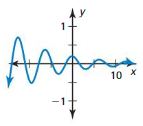
Answer:
![]()
Question 8.

Answer:
The function is a periodic function with a period of 2.
In Exercises 9–12, identify the amplitude and period of the graph of the function.
Question 9.
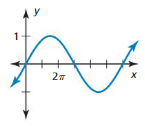
Answer:
![]()
Question 10.
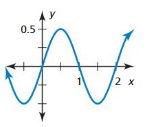
Answer:
The amplitude is 0.5 and the period is 1.
Question 11.
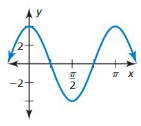
Answer:
![]()
Question 12.
Answer:
The amplitude is 3.5 and the period is 2π.
In Exercises 13–20, identify the amplitude and period of the function. Then graph the function and describe the graph of g as a transformation of the graph of its parent function.
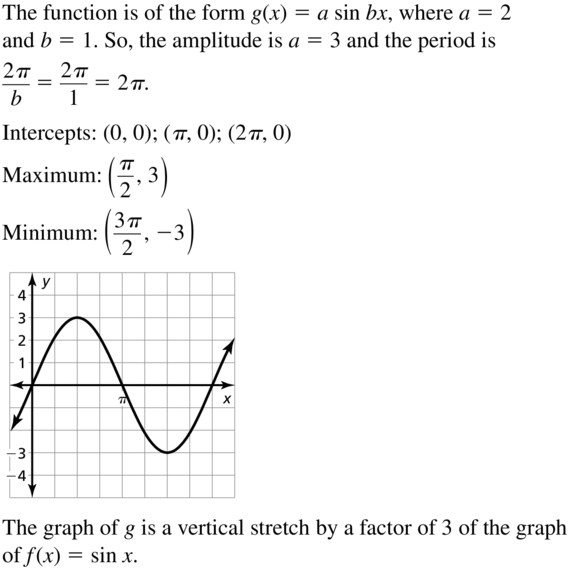
Question 13.
g(x) = 3 sin x
Answer:
Question 14.
g(x) = 2 sin x
Answer:
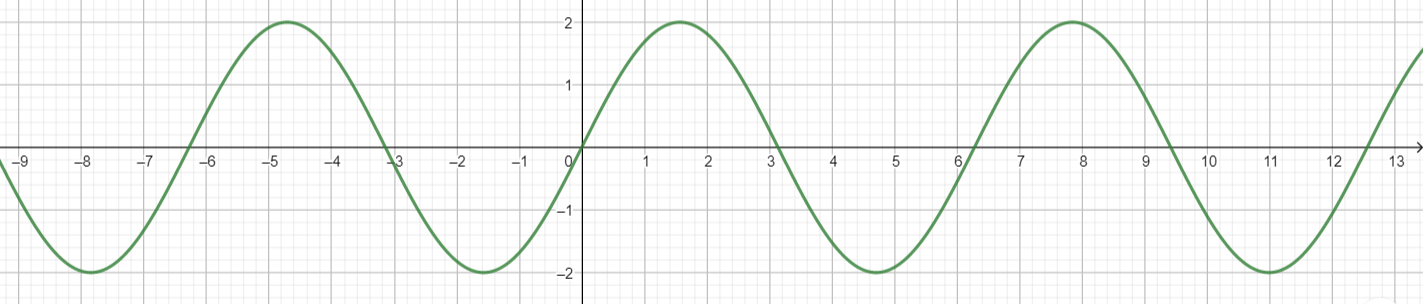
Explnaation:
Amplitude = 2
Period = 3
Minimum = (4.7, -2)
Maximum = (1.5, 2)
Midline = x-axis
Question 15.
g(x) = cos 3x
Answer:
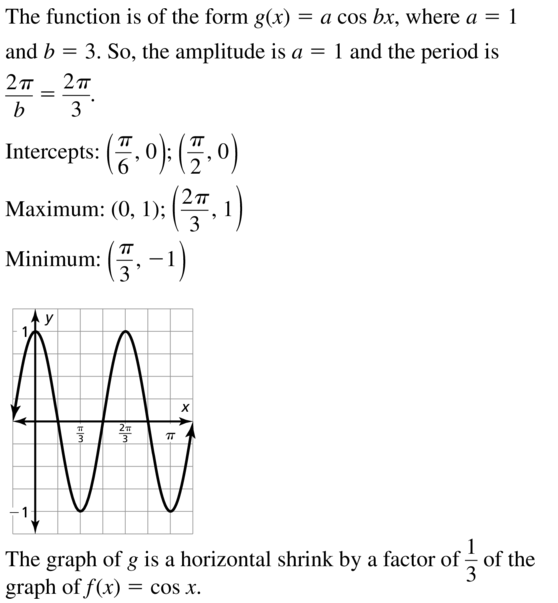
Question 16.
g(x) = cos 4x
Answer:

Explanation:
Amplitude = 1
Period = 1.5
Minimum = (0, -1)
Maximum = (0, 1)
Question 17.
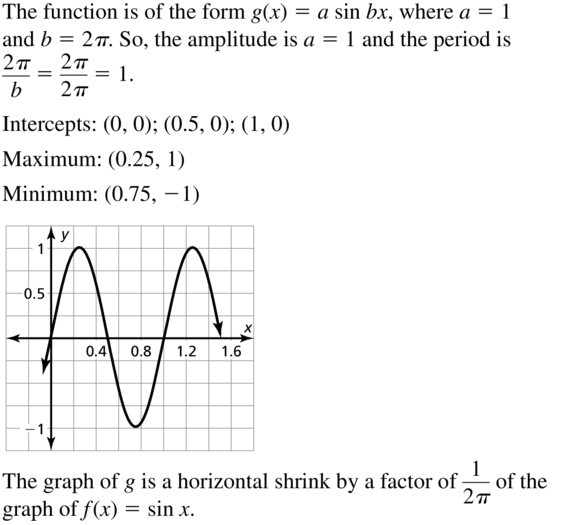
g(x) = sin 2πx
Answer:
Question 18.
g(x) = 3 sin 2x
Answer:

Explanation:
Amplitude = 3
Period = 3
Maximum = (0.78, 3)
Minimum = (2.35, -3)
Question 19.
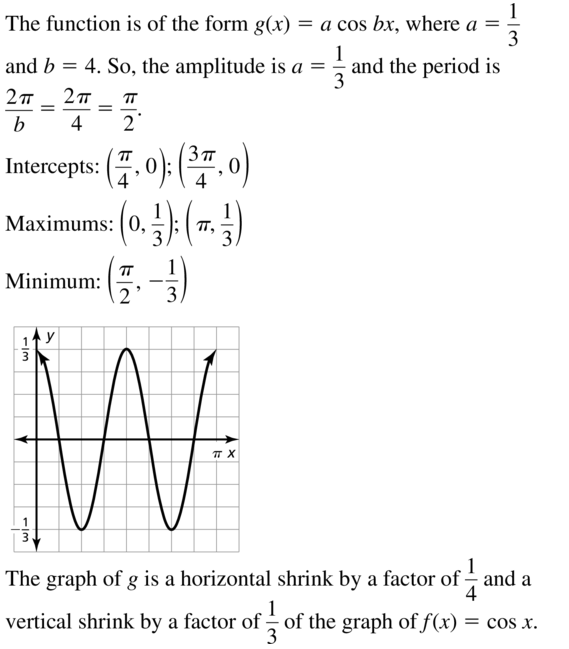
g(x) = \(\frac{1}{3}\)cos 4x
Answer:
Question 20.
g(x) = \(\frac{1}{2}\)cos 4πx
Answer:

Explanation:
Amplitude = 0.5
Period = 0.25
Minimum = (0.25, -0.5)
Maximum = (0.5, 0.5)
Question 21.
ANALYZING EQUATIONS
Which functions have an amplitude of 4 and a period of 2?
A. y = 4 cos 2x
B. y = −4 sin πx
C. y = 2 sin 4x
D. y = 4 cos πx
Answer:
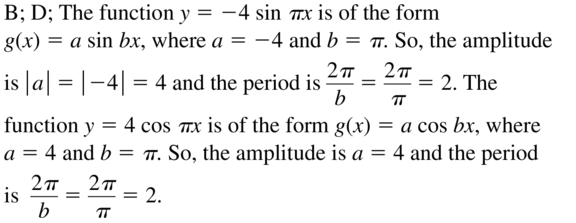
Question 22.
WRITING EQUATIONS
Write an equation of the form y = a sin bx, where a > 0 and b > 0, so that the graph has the given amplitude and period.
a. amplitude: 1
period: 5
b. amplitude: 10
period: 4
c. amplitude: 2
period: 2π
d. amplitude: \(\frac{1}{2}\)
period: 3π
Answer:
a. y = sin (\(\frac { 2πx }{ 5 } \))
b. y = 10 sin (\(\frac { πx }{ 2 } \))
c. y = 2 sinx
y = 0.5 sin (\(\frac { 2x }{ 3 } \))
Explanation:
a. Let’s find the function form of y = a sin(bx), a > 0, b > 0 so that y has an amplitude 1 and period 5.
Amplitude = |a| = 1
So, a = 1 (a > 0)
Period = \(\frac { 2π }{ b } \) = 5
b = \(\frac { 2π }{ 5 } \)
Now the function y is y = sin(\(\frac { 2πx }{ 5 } \))
b. Let’s find the function form of y = a sin(bx), a > 0, b > 0 so that y has an amplitude 10 and period 4
Amplitude = |a| = 10
So, a = 10 (a > 0)
Period = \(\frac { 2π }{ b } \) = 4
b = \(\frac { π }{ 2 } \)
Now the function y is y = 10sin(\(\frac { πx }{ 2 } \))
c. Let’s find the function form of y = a sin(bx), a > 0, b > 0 so that y has an amplitude 2 and period 2π
Amplitude = |a| = 2
So, a = 2 (a > 0)
Period = \(\frac { 2π }{ b } \) = 2π
b = 1
Now the function y is y = 2sin(x)
d. Let’s find the function form of y = a sin(bx), a > 0, b > 0 so that y has an amplitude \(\frac { 1 }{ 2 } \) and period 3π
Amplitude = |a| = \(\frac { 1 }{ 2 } \)
So, a = \(\frac { 1 }{ 2 } \) (a > 0)
Period = \(\frac { 2π }{ b } \) = 3π
b = \(\frac { 2 }{ 3 } \)
Now the function y is y = \(\frac { 1 }{ 2 } \)sin(\(\frac { 2x }{ 3 } \))
Question 23.
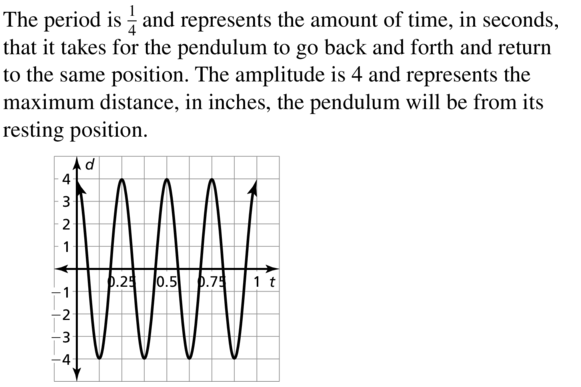
MODELING WITH MATHEMATICS
The motion of a pendulum can be modeled by the function d = 4 cos 8πt, where d is the horizontal displacement (in inches) of the pendulum relative to its position at rest and t is the time (in seconds). Find and interpret the period and amplitude in the context of this situation. Then graph the function.
Answer:
Question 24.
MODELING WITH MATHEMATICS
A buoy bobs up and down as waves go past. The vertical displacement y (in feet) of the buoy with respect to sea level can be modeled by y = 1.75 cos \(\frac{\pi}{3}\)t, where t is the time (in seconds). Find and interpret the period and amplitude in the context of the problem. Then graph the function.

Answer:
The amplitude is 1.75 and the period is 6.
Explanation:
The amplitude and period of the graphs of y = a sin(bx), y = a cos(bx), where a, b are nonzero real numbers, are as follows:
Amplitude : |a|
Period: \(\frac { 2π }{b } \)
The vertical displacement y of the buoy with respect to sea level can be modelled with the following function
y = 1.75 cos (\(\frac { πt }{3 } \))
From the function d, we have that a = 1.75, b = \(\frac { π }{3 } \)a| = |1.75| = 1.75
Period: \(\frac { 2π }{ π/3} \) = 6
Before we graph the function, let’s find the important points. For the intersect points with the x-axis, let’s see the following equation
1.75 cos(\(\frac { πt }{3 } \)) = 0
\(\frac { πt }{3 } \) = \(\frac { π }{2 } \)
So, t = \(\frac { 3 }{2 } \)
xk = \(\frac { 3 }{2 } \) + k
Period = \(\frac { 3 }{2 } \) + 6k
From the minimum and maximum of the function d
1.75 cos(\(\frac { πt }{3 } \)) = 1.75
\(\frac { πt }{3 } \) = 0
tmax = 0
1.75 cos(\(\frac { πt }{3 } \)) = -1.75
\(\frac { πt }{3 } \) = π
tmin = 3
thus, the minimum and maximum points are
tmax = 0 + 6k = 6k
tmin = 3 + 6k
The graph for the function y = 1.75 cos(\(\frac { πt }{3 } \))
The amplitude is 1.75 ft and means that the buoy climbs to 1.75 ft above the sea level and then falls to 1.75 ft below sea level. The period is 6 means it takes 6 seconds from the moment the buoy is at its highest point.
In Exercises 25–34, graph the function.
Question 25.
g(x) = sin x + 2
Answer:
Question 26.
g(x) = cos x − 4
Answer:

Explanation:
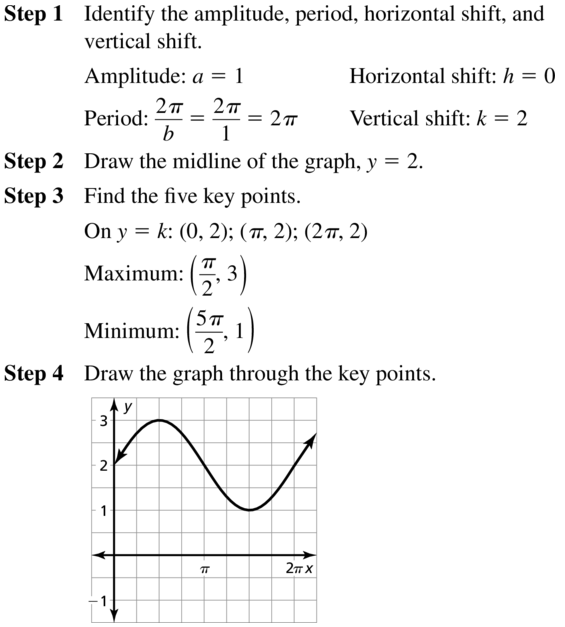
Given function is g(x) = cos x − 4
Here a = 1, b = 1, k = -4
Amplitude = |a| = 1
Period = \(\frac { 2π }{ 1 } \) = 2π
Midline y = -4
Vertical shift = -4
horizontal shift = 0
For the intersect points with the x-axis
cosx – 4 = 0
cos x = 4
Since the equation has no solution for each x we do not have to intersect points with the x-axis
To find minimum amd maximum
cosx – 4 = 3
cos x = 1
xmax = 0
cosx – 4 = -5
cosx = -1
xmin = π
xmax = 0 + 2kπ = 2kπ
xmin = π + 2kπ = (2k + 1)π
Question 27.
g(x) = cos (x − \(\frac{\pi}{2}\))
Answer:
Question 28.
g(x) = sin (x + \(\frac{\pi}{4}\))
Answer:

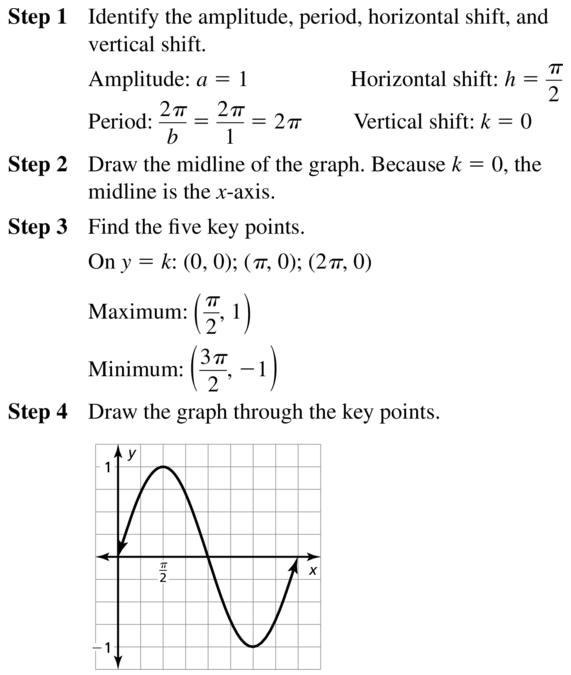
Explanation:
Given function is g(x) = sin (x + \(\frac{\pi}{4}\))
Here a = 1, b = 1, k = 0, h = \(\frac { -π }{ 4 } \)
Amplitude = |a| = 1
Period = \(\frac { 2π }{ 1 } \) = 2π
Midline y = 2
Vertical shift = 0
horizontal shift = \(\frac { -π }{ 4 } \)
For the intersect points with the x-axis
sin(x + \(\frac { π }{ 4 } \)) = 0
x – \(\frac { π }{ 4 } \) = 0
x = \(\frac { π }{ 4 } \)
Thus, the interseting points of the function with the graph will be xk = \(\frac { π }{ 4 } \) + 2kπ
To find minimum amd maximum
sin(x + \(\frac { π }{ 4 } \)) = 1
x + \(\frac { π }{ 4 } \) = \(\frac { π }{ 2 } \)
xmax = \(\frac { π }{ 4 } \)
sin(x + \(\frac { π }{ 4 } \)) = -1
x + \(\frac { π }{ 4 } \) = \(\frac { 3π }{ 2 } \)
xmin = \(\frac { 5π }{ 4 } \)
Thus, minimum and maximum points are
xmax = \(\frac { π }{ 4 } \) + 2kπ
xmin = \(\frac { 5π }{ 4 } \) + 2kπ
Question 29.
g(x) = 2 cos x − 1
Answer:

Question 30.
g(x) = 3 sin x + 1
Answer:
Explanation:
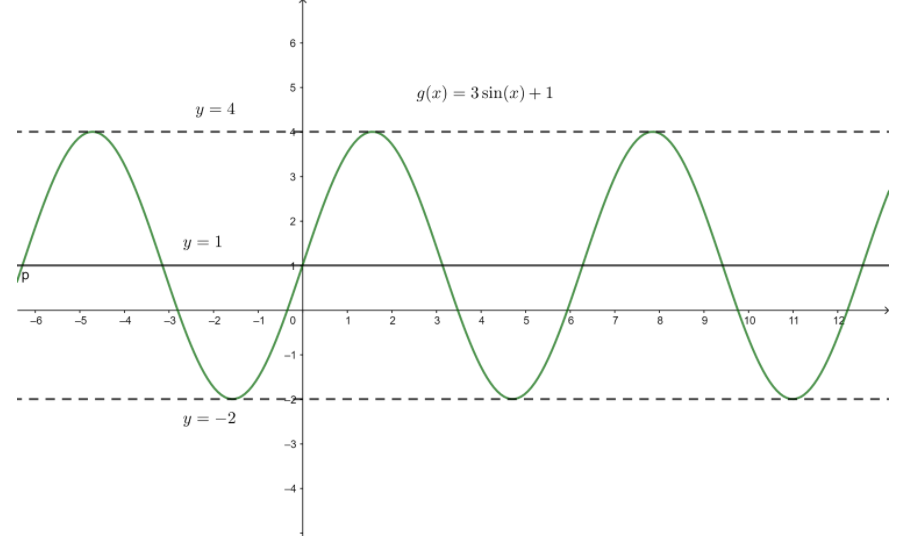
Given function is g(x) = 3 sin x + 1
Here a = 3, b = 1, k = 1, h = 0
Amplitude = |a| = 3
Period = \(\frac { 2π }{ 1 } \) = 2π
Midline y = 1
Vertical shift = 1
horizontal shift = 0
For the intersect points with the x-axis
3 sin x + 1 = 0
3 sin x = -1
sin x = \(\frac { -1 }{ 3 } \)
x = -0.34 radians
Thus, the interseting points of the function with the graph will be xk = -0.34 + 2kπ
To find minimum amd maximum
3 sin x + 1 = 4
3 sinx = 3
xmax = \(\frac { π }{ 2 } \)
3 sin x + 1 = -2
3 sin x = -3
xmin = \(\frac {3π }{ 2 } \)
Thus, minimum and maximum points are
xmax = \(\frac { π }{ 2 } \) + 2kπ
xmin = \(\frac { 3π }{ 2 } \) + 2kπ
Question 31.
g(x) = sin 2(x + π)
Answer:

Question 32.
g(x) = cos 2(x − π)
Answer:
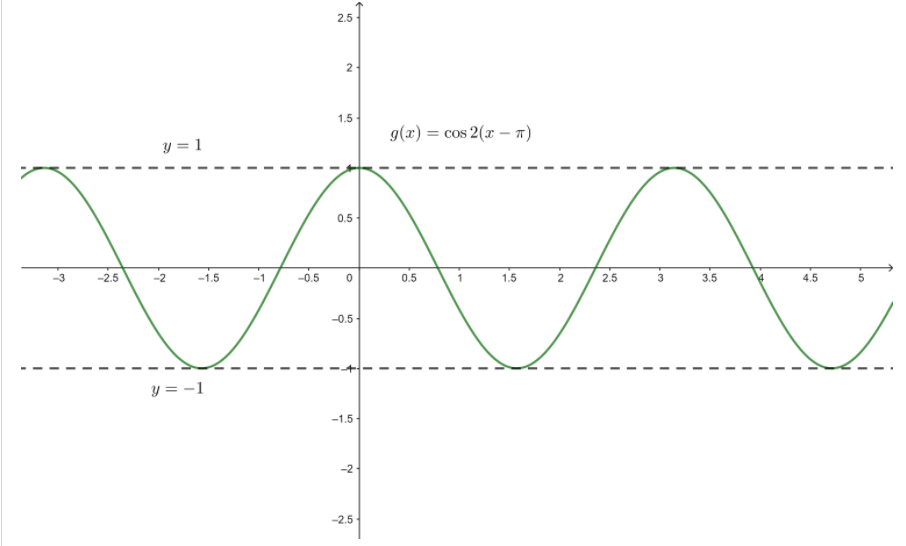
Explanation:
Given function is g(x) = cos 2(x − π)
Here a = 1, b = 2, k = 0, h = π
Amplitude = |a| = 1
Period = \(\frac { 2π }{ 2 } \) = π
Midline y = 0
Vertical shift = 0
horizontal shift = π
For the intersect points with the x-axis
cos 2(x − π) = 0
2(x – π) = \(\frac { π }{ 2 } \)
x – π = \(\frac { π }{ 4 } \)
x = \(\frac { 5π }{ 4 } \)
Thus, the interseting points of the function with the graph will be xk = \(\frac { 5π }{ 4 } \) + 2kπ
To find minimum amd maximum
cos 2(x − π) = 1
2(x − π) = 0
xmax = π
cos 2(x − π) = -1
2(x − π) = π
xmin = \(\frac {3π }{ 2 } \)
Thus, minimum and maximum points are
xmax = π + 2kπ
xmin = \(\frac { 3π }{ 2 } \) + 2kπ
Question 33.
g(x) = sin \(\frac{1}{2}\)(x + 2π) + 3
Answer:

Question 34.
g(x) = cos \(\frac{1}{2}\)(x − 3π) − 5
Answer:
Explanation:
Given function is g(x) = cos \(\frac{1}{2}\)(x − 3π) − 5
Here a = 1, b = 0.5, k = -5, h = 3π
Amplitude = |a| = 1
Period = \(\frac { 2π }{ 0.5 } \) = 4π
Midline y = -5
Vertical shift = -5
horizontal shift = 3π
For the intersect points with the x-axis
cos \(\frac{1}{2}\)(x − 3π) − 5 = 0
cos \(\frac{1}{2}\)(x − 3π) = 5
Since the equation has no solution for each x, we do not have to intersect points with the x-axis.
To find minimum amd maximum
cos \(\frac{1}{2}\)(x − 3π) − 5 = -4
cos \(\frac{1}{2}\)(x − 3π) = 1
\(\frac{1}{2}\)(x − 3π) = 0
xmax = 3π
cos \(\frac{1}{2}\)(x − 3π) − 5 = -6
cos \(\frac{1}{2}\)(x − 3π) = -1
\(\frac{1}{2}\)(x − 3π) = π
xmin = 5π
Thus, minimum and maximum points are
xmax = 3π + 2kπ
xmin = 5π + 2kπ
Question 35.
ERROR ANALYSIS
Describe and correct the error in finding the period of the function y = sin \(\frac{2}{3}\)x.

Answer:
Question 36.
ERROR ANALYSIS
Describe and correct the error in determining the point where the maximum value of the function y = 2 sin (x − \(\frac{\pi}{4}\)) occurs.
Answer:
In the given formula we have that \(\frac { π }{ 2 } \) is subtracted from the x-coordinate of the maximum point but it should be added. Hence the right formula is
Maximum = ((\(\frac { 1 }{ 4 } \) . 2π) + \(\frac { π }{ 2 } \), 2) = (π, 2)
USING STRUCTURE In Exercises 37–40, describe the transformation of the graph of f represented by the function g
Question 37.
f(x) = cos x, g(x) = 2 cos (x − \(\frac{\pi}{2}\)) + 1
Answer:

Question 38.
f(x) = sin x, g(x) = 3 sin (x + \(\frac{\pi}{4}\)) − 2
Answer:
The function f(x) is a parent function of the g(x). Hence, the graph of the function g(x) will be vertical stretched by a fator 3, followed by translation \(\frac { π }{ 4 } \) uits left and 2 units down of the graph of f(x).
Question 39.
f(x) = sin x, g(x) = sin 3(x + 3π) − 5
Answer:

Question 40.
f(x) = cos x, g(x) = cos 6(x − π) + 9
Answer:
The function f(x) is a parent function of the g(x). Hence, the graph of the function g(x) will be horizontally shrink by a factor \(\frac { 1 }{ 6 } \), followed by translation π uits right and 9 units up of the graph of f(x).
In Exercises 41–48, graph the function.
Question 41.
g(x) = −cos x + 3
Answer:

Question 42.
g(x) = −sin x − 5
Answer:
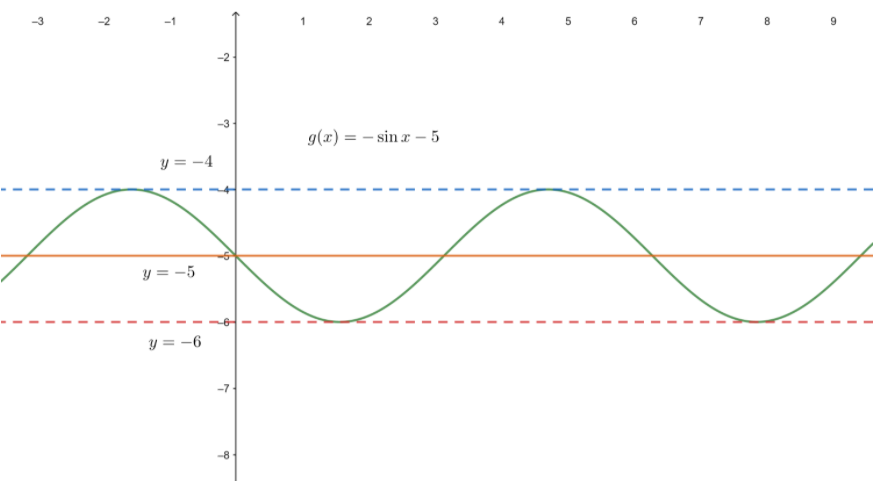
Explanation:
Given function is g(x) = −sin x − 5
Here a = -1, b = 1, k = -5, h = 0
Amplitude = |a| = |-1| = 1
Period = \(\frac { 2π }{ 1 } \) = 2π
Midline y = -5
Vertical shift = -5
horizontal shift = 0
Draw the midline y = -5. The intersect points of g(x) with the midline will be (π, -5), (2π, -5)
Since the midline of g(x) is y = -5, the upper limit of the function is k + |a| = -5 + 1 = -4 and the lower limit is k – |a| = -5 – 1 = -6
Hence, the minimum and maximum will be
Maximum = (\(\frac { π }{ 2 } \), -4)
minimum = (\(\frac { 3π }{ 2 } \), -6)
Because a = -1 < 0 the graph is reflected in the midline y = -5
We have
(\(\frac { π }{ 2 } \), -4) becomes ((\(\frac { π }{ 2 } \), -6) (minimum)
(\(\frac { 3π }{ 2 } \), -6) becomes (\(\frac { 3π }{ 2 } \), -4) (maximum)
Question 43.
g(x) = −sin \(\frac{1}{2}\)x − 2
Answer:

Question 44.
g(x) = −cos 2x + 1
Answer:
Explanation:
Given function is g(x) = −cos 2x + 1
Here a = -1, b = 2, k = 1, h = 0
Amplitude = |a| = |-1| = 1
Period = \(\frac { 2π }{ 2 } \) = π
Midline y = 1
Vertical shift = 1
horizontal shift = 0
Draw the midline y = 1. The intersect points of g(x) with the midline will be (\(\frac { π }{ 4 } \), 1), (\(\frac { 3π }{ 4 } \), 1)
Since the period is π, we will draw the following points
(\(\frac { π }{ 4 } \) +kπ, 1), (\(\frac { 3π }{ 4 } \)+kπ, 1)
the minimum and maximum will be
Maximum = (\(\frac { 2π }{ 2 } \), 1 + 1) = (π, 2)
minimum = (\(\frac { 2π }{ 4 } \), 1 – 1) = (\(\frac { π }{ 2 } \), 0)
Because a = -1 < 0 the graph is reflected in the midline y = 1
We have
(\(\frac { π }{ 2 } \), 0) becomes ((\(\frac { π }{ 2 } \), 2) (maximum)
(π, 2) becomes (π, 0) (minimum)
Since the period is π, we will draw the following points
(π +kπ, 0), (\(\frac { π }{ 2 } \)+kπ, 2)
Question 45.
g(x) = −sin(x − π) + 4
Answer:

Question 46.
g(x) = −cos(x + π) − 2
Answer:
Explanation:
Given function is g(x) = −cos(x + π) − 2
Here a = -1, b = 1, k = -2, h = -π
Amplitude = |a| = |-1| = 1
Period = \(\frac { 2π }{ 1 } \) = 2π
Midline y = -2
Vertical shift = -2
horizontal shift = -π
Draw the midline y = -2. The intersect points of g(x) with the midline will be (\(\frac { -π }{ 2 } \), -2), (\(\frac { π }{ 2 } \), -2)
Since the period is 2π, we will draw the following points
(\(\frac { -π }{ 2 } \) +2kπ, -2), (\(\frac { π }{ 2 } \)+2kπ, -2)
Since the midline of g(x) is y = -2, the upper limirt is 2 + 1 = -1 and lower limit is -2 – 1 = -3
the minimum and maximum will be
Maximum = (\(\frac { 2π }{ 1 } \), -2 – 1) = (2π, -3)
minimum = (\(\frac { 2π }{ 2 } \), -2 + 1) = (π, -1)
Because a = -1 < 0 the graph is reflected in the midline y = 3
We have
(2π, -3) becomes (2π, -1)
(π, -1) becomes (π, -3)
Since the period is 2π, we will draw the following points
(2π +2kπ, 2), (π+2kπ, 4)
Question 47.
g(x) = −4 cos (x + \(\frac{\pi}{4}\)) − 1
Answer:
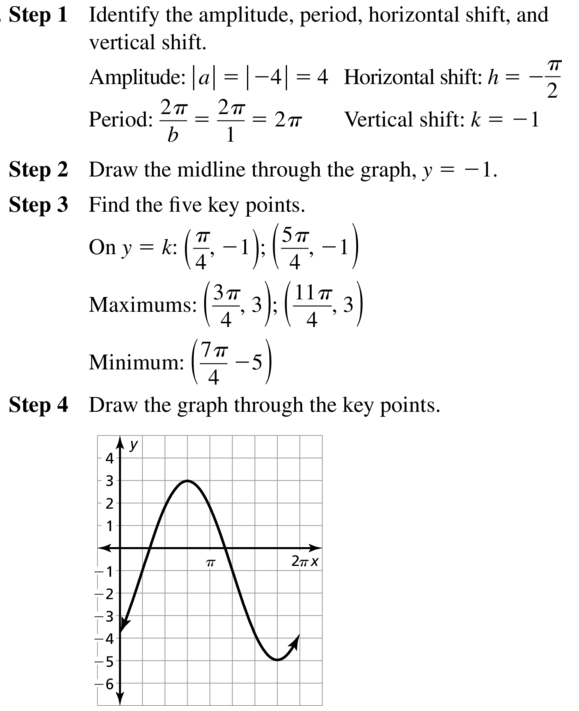
Question 48.
g(x) = −5 sin (x − \(\frac{\pi}{2}\)) + 3
Answer:
Explanation:
Given function is g(x) = −5 sin (x − \(\frac{\pi}{2}\)) + 3
Here a = -5, b = 1, k = 3, h = \(\frac { π }{ 2 } \)
Amplitude = |a| = |-5| = 5
Period = \(\frac { 2π }{ 1 } \) = 2π
Midline y = 3
Vertical shift = 3
horizontal shift = \(\frac { π }{ 2 } \)
Draw the midline y = 3. The intersect points of g(x) with the midline will be (\(\frac { π }{ 2 } \), 3), (\(\frac { 3π }{ 2 } \), 3)
Since the period is 2π, we will draw the following points
(\(\frac { π }{ 2 } \) +2kπ, 3), (\(\frac { 3π }{ 2 } \)+2kπ, 3)
Since the midline of g(x) is y = 3, the upper limirt is 3 + 5 = 8 and lower limit is 3 – 5 = -2
the minimum and maximum will be
Maximum = (π, 8)
minimum = (2π, -2)
Because a = -5 < 0 the graph is reflected in the midline y = 3
We have
(π, 8) becomes (π, -2)
(2π, -2) becomes (2π, 8)
Since the period is 2π, we will draw the following points
(2π +2kπ, -2), (2π+2kπ, 8)
Question 49.
USING EQUATIONS
Which of the following is a point where the maximum value of the graph of y =−4 cos (x − \(\frac{\pi}{2}\))occurs?
A. (−\(\frac{\pi}{2}\), 4 )
B. (\(\frac{\pi}{2}\), 4 )
C. (0, 4)
D. (π, 4)
Answer:

Question 50.
ANALYZING RELATIONSHIPS
Match each function with its graph. Explain your reasoning.
a. y = 3 + sin x
b. y = −3 + cos x
c. y = sin 2(x − \(\frac{\pi}{2}\))
d. y = cos 2 (x − \(\frac{\pi}{2}\))
Answer:
a – B
b – C
c – A
d – D
Explanation:
a. The function y = 3 + sin x, represents the graph of the sin x translated 3 units up. Hence the function matches with graph B.
b. The function y = −3 + cos x, represent the graph of the cos x translated 3 units down. Hence the function matches with graph C.
c. The function y = sin 2(x − \(\frac{\pi}{2}\)), represent the graph of the sin x which is horizontally shrink by a fcator 0.5 and horizontally shifted by \(\frac { π }{ 2 } \) units right. Hence the function matches with the graph A.
d. The function y = cos 2 (x − \(\frac{\pi}{2}\)), represent the graph of the cos x which is horizontally shrink by a fcator 0.5 and horizontally shifted by \(\frac { π }{ 2 } \) units right. Hence the function matches with the graph D.
WRITING EQUATIONS In Exercises 51–54, write a rule for g that represents the indicated transformations of the graph of f.
Question 51.
f(x) = 3 sin x; translation 2 units up and π units right
Answer:
![]()
Question 52.
f(x) = cos 2πx; translation 4 units down and 3 units left
Answer:
The transformation is f(x) = cos (2π(x + 3)) – 4
Question 53.
f(x) = \(\frac{1}{3}\)cos πx; translation 1 unit down, followed by a reflection in the line y =−1
Answer:
![]()
Question 54.
f(x) = \(\frac{1}{2}\) sin 6x; translation \(\frac{3}{2}\) units down and 1 unit right, followed by a reflection in the line y = −\(\frac{3}{2}\)
Answer:
The transformation is f(x) = \(\frac{1}{2}\) sin(6(xx – 1)) – \(\frac { 3 }{ 2 } \)
Question 55.
MODELING WITH MATHEMATICS
The height h(in feet) of a swing above the ground can be modeled by the function h = −8 cos θ+ 10, where the pivot is 10 feet above the ground, the rope is 8 feet long, and θ is the angle that the rope makes with the vertical. Graph the function. What is the height of the swing when θ is 45°?

Answer:
Question 56.
DRAWING A CONCLUSION
In a particular region, the population L (in thousands) of lynx (the predator) and the population H (in thousands) of hares (the prey) can be modeled by the equations
L = 11.5 + 6.5 sin\(\frac{\pi}{5}\)t
H = 27.5 + 17.5 cos \(\frac{\pi}{5}\)t
where t is the time in years.
a. Determine the ratio of hares to lynx when t = 0, 2.5, 5, and 7.5 years.
b. Use the figure to explain how the changes in the two populations appear to be related.
Answer:
a. \(\frac { 45 }{ 11.5 } \), \(\frac { 27.5 }{ 18 } \), \(\frac { 10 }{ 11.5 } \), \(\frac { 27.5 }{ 5 } \)
b. When the number of lines reaches a maximum and starts to decreases, the number of hares decreases to a minimum. At this point, the number of hares begins to grow to its midline, and the number of lynx reduces until it reaches its minimum. the number of lynx then begins to grow as the number of hares reaches a maximum.
Explanation:
Given that
L(t) = 11.5 + 6.5 sin\(\frac{\pi}{5}\)t
H(t) = 27.5 + 17.5 cos \(\frac{\pi}{5}\)t
\(\frac { H(0) }{ L(0) } \) = \(\frac { 27.5 + 17.5 cos(0) }{ 11.5 + 6.5 sin(0) } \)
= \(\frac { 27.5 + 17.5 x 1 }{ 11.5 + 6.5 x 0 } \)
= \(\frac { 45 }{ 11.5 } \)
The ratio of hares to lynx when t = 2.5 = \(\frac { 5 }{ 2 } \)
H(\(\frac { 5 }{ 2 } \)) : L(\(\frac { 5 }{ 2 } \)) = 27.5 + 17.5 cos (\(\frac{\pi}{5}\) . \(\frac { 5 }{ 2 } \)) : 11.5 + 6.5 sin(\(\frac{\pi}{5}\) . \(\frac { 5 }{ 2 } \))
= 27.5 + 17.5 x 0 : 11.5 + 6.5 x 1
= 27.5 : 18
If t = 5
\(\frac { H(5) }{ L(5) } \) = \(\frac { 27.5 + 17.5 cos π }{ 11.5 + 6.5 sin π } \)
= \(\frac { 27.5 + 17.5 (-1) }{ 11.5 + 6.5 (0)} \)
= \(\frac { 10 }{ 11.5 } \)
When t = 7.5
\(\frac { H(7.55) }{ L(7.55) } \) = \(\frac { 27.5 + 17.5 (0) }{ 11.5 + 6.5 (-1)} \)
= \(\frac { 27.5 }{ 5 } \)
b. Let’s consider the given image that contains the graphs of the functions H and L. We can see that, when the number of lynx is in the middle abd increases, the number of hares decreases. Now, when the no of lynx reaches a maximum it’s starting to decreases, the number of hares decreases to a minimum.
Question 57.
USING TOOLS
The average wind speed s (in miles per hour) in the Boston Harbor can be approximated by s = 3.38 sin\(\frac{\pi}{180}\)(t + 3) + 11.6 where t is the time in days and t = 0 represents January 1. Use a graphing calculator to graph the function. On which days of the year is the average wind speed 10 miles per hour? Explain your reasoning.
Answer:
Question 58.
USING TOOLS
The water depth d (in feet) for the Bay of Fundy can be modeled by d = 35 − 28 cos \(\frac{\pi}{6.2}\)t, where t is the time in hours and t = 0 represents midnight. Use a graphing calculator to graph the function. At what time(s) is the water depth 7 feet? Explain.

Answer:
The graph of the function d(t) = 35 – 28 cos(\(\frac { π }{ 6.2 } \))t
The depth of the water is in the coordinates (0, 7) and (12.4, 7)
Explanation:
the water depth d (in feet) is modeled by the following function
d(t) = 35 – 28 cos(\(\frac { π }{ 6.2 } \))t
By using the graphic calculator, lets sketch the graph of the function d(t)
Since d(t) represents the water depth of the wind at the moment t, thus to find the moment when the depth is equal to 7 ft, we draw the line y = 7 and function d(t). Hence by using the graphic calculator, we obtain that the intersect points are (0, 7) and (12.4, 7)
Question 59.
MULTIPLE REPRESENTATIONS
Find the average rate of change of each function over the interval 0 < x < π.
a. y = 2 cos x

Answer:

Question 60.
REASONING
Consider the functions y = sin(−x) and y = cos(−x).
a. Construct a table of values for each equation using the quadrantal angles in the interval −2π ≤ x ≤ 2π.
b. Graph each function.
c. Describe the transformations of the graphs of the parent functions.
Answer:
The cosine is an even function and the sine is an odd function.
Explanation:
a. draw a table for f(x) = sin(-x), g(x) = cos(-x) in the interval [-2π, 2π]
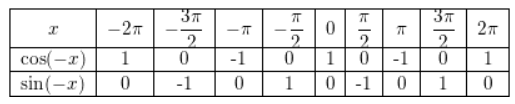
b.
c. From the graphs, we can see that graph for y = cos(-x) matches the graph for y = cos x which implies that stand cosx = cos(-x). For graph y = sin(-x) we can notice that stands sin(-x) = -sinx which implies that functions reflect above the graph of sin(-x) reflect about the midline.
Question 61.
MODELING WITH MATHEMATICS
You are riding a Ferris wheel that turns for 180 seconds. Your height h (in feet) above the ground at any time t (in seconds) can be modeled by the equation h = 85 sin\(\frac{\pi}{20}\)(t − 10) + 90.

a. Graph the function.
b. How many cycles does the Ferris wheel make in 180 seconds?
c. What are your maximum and minimum heights?
Answer:
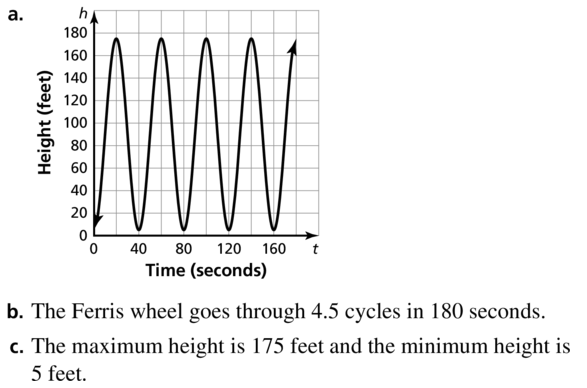
Question 62.
HOW DO YOU SEE IT?
Use the graph to answer each question.

a. Does the graph represent a function of the form f(x) = a sin bx or f(x) =a cos bx? Explain.
b. Identify the maximum value, minimum value, period, and amplitude of the function.
Answer:
a. f(x) = 5 cos(2x)
b. Amplitude is 5, the period is π, minimum is -5 and maximum is 5.
Explanation:
a. From the graph x = 0
f(x) = a sin(0) = 0
a cos(b . 0) = 5
a cos 0 = 5
a x 1 = 5
a = 5
We notice that the period of function is π
\(\frac { 2π }{ b } \) = π
b = 2
the function is f(x) = 5 cos 2x
b. the amplitude and period of f(x) are 5, π. The midline of function is x-axis, the minimum value is -5 and maximum is 5
Question 63.
FINDING A PATTERN
Write an expression in terms of the integer n that represents all the x-intercepts of the graph of the function y = cos 2x. Justify your answer.
Answer:

Question 64.
MAKING AN ARGUMENT
Your friend states that for functions of the form y = a sin bx and y = a cos bx, the values of a and b affect the x-intercepts of the graph of the function. Is your friend correct? Explain.
Answer:
My friend is not correct.
a does not affect the x-intercepts, b affect the x-intercepts.
Question 65.
CRITICAL THINKING
Describe a transformation of the graph of f(x) = sin x that results in the graph of g(x) = cos x.
Answer:

Question 66.
THOUGHT PROVOKING
Use a graphing calculator to find a function of the form y = sin b1x + cos b2xwhose graph matches that shown below.

Answer:
y = sinx + cos2x
Question 67.
PROBLEM SOLVING
For a person at rest, the blood pressure P (in millimeters of mercury) at time t (in seconds) is given by the function
P = 100 − 20 cos \(\frac{8 \pi}{3}\)t.
Graph the function. One cycle is equivalent to one heartbeat. What is the pulse rate (in heartbeats per minute) of the person?

Answer:
Question 68.
PROBLEM SOLVING
The motion of a spring can be modeled by y = A cos kt, where y is the vertical displacement (in feet) of the spring relative to its position at rest, A is the initial displacement (in feet), k is a constant that measures the elasticity of the spring, and t is the time (in seconds).
a. You have a spring whose motion can be modeled by the function y= 0.2 cos 6t. Find the initial displacement and the period of the spring. Then graph the function.
b. When a damping force is applied to the spring, the motion of the spring can be modeled by the function y = 0.2e−4.5t cos 4t. Graph this function. What effect does damping have on the motion?
Answer:
a. The initial displacement is 0.2 nad period is \(\frac { π }{3 } \)
b. The motion is imperceptible as the displacement decreases to zero.
Explanation:
a. The motion of the spring can be modeled by the following function
y = 0.2 cos(6t)
From the given model, y = Acos(kt), A = 0.2, k = 6. The initial displaceent is 0.2 ft.
Period = \(\frac { 2π }{ 6 } \) = \(\frac { π }{ 3 } \)
The graph for y = 0.2cos(6t)
b. When a damping force is applied to the spring, the motion of the spring can be modeled with y = 0.2 e^-4.5t cos(4t)
The graph is
Maintaining Mathematical Proficiency
Simplify the rational expression, if possible.
Question 69.
\(\frac{x^{2}+x-6}{x+3}\)
Answer:
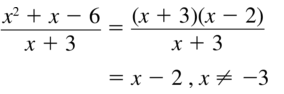
Question 70.
\(\frac{x^{3}-2 x^{2}-24 x}{x^{2}-2 x-24}\)
Answer:
x^{3}-2 x^{2}-24 x = x(x² – 2x – 24)
\(\frac{x^{3}-2 x^{2}-24 x}{x^{2}-2 x-24}\) = \(\frac{x(x – 4)(x + 6)}{(x – 4)(x + 6)}\)
= x
Question 71.
\(\frac{x^{2}-4 x-5}{x^{2}+4 x-5}\)
Answer:
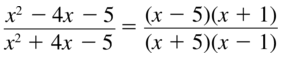
Question 72.
\(\frac{x^{2}-16}{x^{2}+x-20}\)
Answer:
Find the least common multiple of the expressions.
Question 73.
2x, 2(x − 5)
Answer:
![]()
Question 74.
x2 − 4, x + 2
Answer:
x2 − 4 = (x + 2)(x – 2)
The least common multiple of x2 − 4, x + 2 is (x + 2)(x – 2)
Question 75.
x2 + 8x + 12, x + 6
Answer:
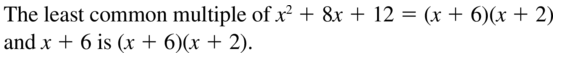
Trigonometric Ratios and Functions Study Skills: Form a Final Exam Study Group
9.1–9.4 What Did You Learn?
Core Vocabulary

Core Concepts

Mathematical Practices
Question 1.
Make a conjecture about the horizontal distances traveled in part (c) of Exercise 39 on page 483.
Answer:
Question 2.
Explain why the quantities in part (a) of Exercise 56 on page 493 make sense in the context of the situation.
Answer:
Study Skills: Form a Final Exam Study Group
Form a study group several weeks before the final exam. The intent of this group is to review what you have already learned while continuing to learn new material.

Trigonometric Ratios and Functions 9.1–9.4 Quiz
Question 1.
In a right triangle, θ is an acute angle and sin θ = \(\frac{1}{2}\). Evaluate the other five trigonometric functions of θ.
Answer:
Find the value of x for the right triangle.
Question 2.
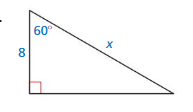
Answer:
x = 16
Explanation:
cos 60 = \(\frac { 8 }{ x } \)
0.5 = \(\frac { 8 }{ x } \)
x = 16
Question 3.
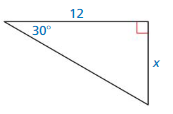
Answer:
x = 6.92
Explanation:
tan 30 = \(\frac { x }{ 12 } \)
0.577 = \(\frac { x }{ 12 } \)
x = 6.92
Question 4.
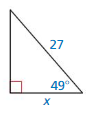
Answer:
x = 17.55
Explanation:
cos 49 = \(\frac { x }{ 27 } \)
0.65 = \(\frac { x }{ 27 } \)
x = 17.55
Draw an angle with the given measure in standard position. Then find one positive angle and one negative angle that are coterminal with the given angle.
Question 5.
40°
Answer:
Positive angle = 40 + 360 = 400°
negative angle = 40 – 360 = -320°
Question 6.
\(\frac{5 \pi}{6}\)
Answer:
Positive angle = \(\frac{5 \pi}{6}\) + 2π = \(\frac{17 \pi}{6}\)
Negative angle = \(\frac{5 \pi}{6}\) – 2π = \(\frac{-7 \pi}{6}\)
Question 7.
−960°
Answer:
Positive angle = -960 + 360 = -600°
Negative angle = -960 – 360 = -1320°
Convert the degree measure to radians or the radian measure to degrees.
Question 8.
\(\frac{3 \pi}{10}\)
Answer:
\(\frac{3 \pi}{10}\) = \(\frac{3 \pi}{10}\) x \(\frac { 180 }{ π } \)
= 54°
Question 9.
−60°
Answer:
−60° = −60° x \(\frac { π }{ 180 } \)
= \(\frac { -π }{ 3 } \)
Question 10.
72°
Answer:
72° = 72° x \(\frac { π }{ 180 } \)
= \(\frac { 2π }{ 5 } \)
Evaluate the six trigonometric functions of θ.
Question 11.
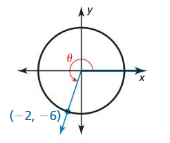
Answer:
sin θ = \(\frac { 3 }{ √10 } \)
cos θ = \(\frac { -1 }{ √10 } \)
tan θ = -3
cot θ = \(\frac { -1 }{ 3 } \)
sec θ = -√10
csc θ = \(\frac { √10}{ 3 } \)
Explanation:
r = √(-2)² + (-6)² = 2√10
x = -2, y = -6
sin (360 – θ) = \(\frac { y }{ r } \) = \(\frac { -6 }{ 2√10 } \)
cos (360 – θ) = \(\frac { x }{ r } \) = \(\frac { -2 }{ 2√10} \)
tan (360 – θ) = \(\frac { y }{ x } \) = \(\frac { -6 }{ -2 } \)
cot (360 – θ) = \(\frac { x }{ y } \) = \(\frac { -2 }{ -6 } \)
sec (360 – θ) = \(\frac { r }{ x } \) = \(\frac { 2√10 }{ -2 } \)
csc (360 – θ) = \(\frac { r }{ y } \) = \(\frac { 2√10}{ -6 } \)
Question 12.
Answer:
Sin \(\frac { π }{ 2 } \) = 1
cos \(\frac { π }{ 2 } \) = 0
tan \(\frac { π }{ 2 } \) = 1.633
cot \(\frac { π }{ 2 } \) = 0
sec \(\frac { π }{ 2 } \) = undefined
csc \(\frac { π }{ 2 } \) = 1
Question 13.
Answer:
Sin \(\frac { 2π }{ 3 } \) = 0.866
cos \(\frac { 2π }{ 3 } \) = -0.5
tan \(\frac { 2π }{ 3 } \) = -1.73
cot \(\frac { 2π }{ 3 } \) = \(\frac { -√3 }{ 3 } \)
sec \(\frac { 2π }{ 3 } \) = -2
csc \(\frac { 2π }{ 3 } \) = \(\frac { 2√3 }{ 3 } \)
Question 14.
Identify the amplitude and period of g(x) = 3 sin x. Then graph the function and describe the graph of g as a transformation of the graph of f (x) = sin x.
Answer:
The period is 2π, the amplitude is 3

Explanation:
g(x) = 3 sin x
a = 3, b = 1
Amplitude = 3
Period = \(\frac { 2π }{ b } \) = \(\frac { 2π }{ 1 } \) = 2π
Question 15.
Identify the amplitude and period of g(x) = cos 5πx + 3. Then graph the function and describe the graph of g as a transformation of the graph of f(x) = cos x.
Answer:

Amplitude = 1
Period = \(\frac { 2π }{ 5π } \) = \(\frac { 2 }{ 5 } \)
Question 16.
You are flying a kite at an angle of 70°. You have let out a total of 400 feet of string and are holding the reel steady 4 feet above the ground.
a. How high above the ground is the kite?
b. A friend watching the kite estimates that the angle of elevation to the kite is 85°. How far from your friend are you standing?
Answer:
a. 375.88 ft high above the ground is the kite.
b. 170 ft
Explanation:
a. h + 4 = 400 sin 70
h + 4 = 379.88
h = 375.88
b. d = 400 cos 70
= 136.8
The distance of my friend from me D = 136.8 + 379.87 tan 85
= 170 ft
Question 17.
The top of the Space Needle in Seattle, Washington, is a revolving, circular restaurant. The restaurant has a radius of 47.25 feet and makes one complete revolution in about an hour. You have dinner at a window table from 7:00 P.M. to 8:55 P.M. Compare the distance you revolve with the distance of a person seated 5 feet away from the windows.
Answer:
No distance is less
Explanation:
Points closer to the center of the rotation do not need to travel as far to complete one revolution.
\(\frac { 23 }{ 12 } \) x 2π(47.25) = 569 ft
And reduce r by 5 ft
\(\frac { 23 }{ 12 } \) x 2π(47.25 – 5) = 5.9 ft
It is clearly less
Lesson 9.5 Graphing Other Trigonometric Functions
Essential Question What are the characteristics of the graph of the tangent function?
EXPLORATION 1
Graphing the Tangent Function
Work with a partner. a. Complete the table for y = tan x, where x is an angle measure in radians.
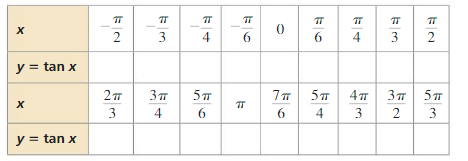
b. The graph of y = tan x has vertical asymptotes at x-values where tan x is undefined. Plot the points (x, y) from part (a). Then use the asymptotes to sketch the graph of y = tan x.
c. For the graph of y = tan x, identify the asymptotes, the x-intercepts, and the intervals for which the function is increasing or decreasing over −\(\frac{\pi}{2}\) ≤ x ≤ \(\frac{3 \pi}{2}\). Is the tangent function even, odd, or neither?
Communicate Your Answer
Question 2.
What are the characteristics of the graph of the tangent function?
Answer:
Question 3.
Describe the asymptotes of the graph of y = cot x on the interval −\(\frac{\pi}{2}\) < x < \(\frac{3 \pi}{2}\).

Answer:
Monitoring Progress
Graph one period of the function. Describe the graph of g as a transformation of the graph of its parent function.
Question 1.
g(x) = tan 2x
Answer:
Explanation:
Given that,
g(x) = tan 2x
The function is in the form of g(x) = atan(bx)
a = 1, b = 2
Period = \(\frac { π }{ b } \) = \(\frac { π }{ 2 } \)
The x-intercepts are (0 + \(\frac { kπ }{ 2 } \), 0) = \(\frac { kπ }{ 2 } \), 0)
The halfway points are
(\(\frac { π }{ 4b } \), a) = (\(\frac { π }{ 8 } \), 1)
(\(\frac { -π }{ 4b } \), -a) = (\(\frac { -π }{ 8 } \), -1)
The vertical asymptotes are odd multiples of \(\frac { π }{ 2|b| } \)
x = \(\frac { π }{ 4 } \)
x = \(\frac { -π }{ 4 } \)
The graph of g(x) is a horizontal shrink by a factor of 0.5 of the graph of the function f(x) = tan x
Question 2.
g(x) = \(\frac{1}{3}\)cot x
Answer:
Explanation:
Given that,
g(x) = \(\frac{1}{3}\)cot x
The function is in the form of g(x) = acot(bx)
a = \(\frac{1}{3}\), b = 1
Period = \(\frac { π }{ b } \) = \(\frac { π }{ 1 } \) = π
The x-intercepts point of the general function is (\(\frac { π }{ 2b } \), 0) = (\(\frac { π }{ 2 } \), 0) and since the period is 3π, the x-intercepts are (\(\frac { π }{ 2 } \) + 3π, 0)
The halfway points are
(\(\frac { π }{ 4b } \), a) = (\(\frac { π }{ 4 } \), \(\frac{1}{3}\))
(\(\frac { -π }{ 4b } \), -a) = (\(\frac { -π }{ 4 } \), –\(\frac{1}{3}\))
The vertical asymptotes are at a multiples of \(\frac { π }{ 2|b| } \)
x = 0
x = π
The graph of g(x) is a horizontal shrink by a factor of \(\frac{1}{3}\) of the graph of the function f(x) = cot x
Question 3.
g(x) = 2 cot 4x
Answer:
Explanation:
Given that,
g(x) = 2 cot 4x
The function is in the form of g(x) = acot(bx)
a = 2, b = 4
Period = \(\frac { π }{ b } \) = \(\frac { π }{ 4 } \)
The x-intercepts point of the general function is (\(\frac { π }{ 2b } \), 0) = (\(\frac { π }{ 8 } \), 0) and since the period is \(\frac { π }{ 4 } \), the x-intercepts are (\(\frac { π }{ 8 } \) + \(\frac { πk }{ 4 } \), 0)
The halfway points are
(\(\frac { π }{ 4b } \), a) = (\(\frac { π }{ 8 } \), 2)
(\(\frac { -π }{ 4b } \), -a) = (\(\frac { -π }{ 8 } \), -2)
The vertical asymptotes are at a multiples of \(\frac { π }{ |b| } \)
x = \(\frac { -π }{ 4 } \)
x = 0
x = \(\frac { π }{ 4 } \)
The graph of g(x) is a horizontal shrink by a factor of \(\frac{1}{4}\) followed by a vertically strech of the graph of the function f(x) = cot x
Question 4.
g(x) = 5 tan πx
Answer:
Explanation:
Given that,
g(x) = 5 tan πx
The function is in the form of g(x) = atan(bx)
a = 5, b = π
Period = \(\frac { π }{ b } \) = \(\frac { π }{ π } \) = 1
The x-intercepts point of the general function is (0, 0) and since the period is π,
The x-intercepts are (0 + k, 0 + k) = (kπ, kπ)
The halfway points are
(\(\frac { π }{ 4b } \), a) = (\(\frac { 1 }{ 4 } \), 5)
(\(\frac { -π }{ 4b } \), -a) = (\(\frac { -1 }{ 4 } \), -5)
The vertical asymptotes are at a multiples of \(\frac { π }{ 2|b| } \)
x = \(\frac { 1 }{ 2 } \)
x = \(\frac { -1 }{ 2 } \)
The graph of g(x) is a vertical stretch by a factor of 5 followed by a horizontally stretch of the graph of the function f(x) = tan x
Graph one period of the function. Describe the graph of g as a transformation of the graph of its parent function.
Question 5.
g(x) = csc 3x
Answer:
Explanation:
Given that
g(x) = csc 3x
Let’s graph the function f(x) = sin3x
Period is \(\frac { 2π }{ 3 } \), amplitude is 1, midline is x-axis
The x-intercepts are xk = \(\frac { kπ }{ 3 } \)
Maximum = (\(\frac { π }{ 6 } \) + \(\frac { 2π }{ 3 } \), 1)
Minimum = (\(\frac { -π }{ 6 } \) + \(\frac { 2π }{ 3 } \), -1)
The graph of f(x) is
the asymptotes of g(x) are
x = 0
x = \(\frac { π }{ 3 } \)
x = \(\frac { -π }{ 3 } \)
Now let’s plot the points where f(x) = sin3x reaches maximum and minimum value
these points are (\(\frac { π }{ 6 } \), 1), \(\frac { -π }{ 6 } \), -1)
Question 6.
g(x) = \(\frac{1}{2}\)sec x
Answer:
Explanation:
Given that
g(x) = \(\frac{1}{2}\)sec x
Let’s graph the function f(x) = \(\frac{1}{2}\)cosx
Period is π, amplitude is 0.5, midline is x-axis
The x-intercepts are xk = \(\frac { π }{ 2 } \) + 2k
Maximum = (0, \(\frac { 1 }{ 2 } \))
Minimum = (π, –\(\frac { 1 }{ 2 } \))
The graph of f(x) is
the asymptotes of g(x) are
x = \(\frac { π }{ 2 } \)
x = \(\frac { -π }{ 2 } \)
Now let’s plot the points where f(x) = \(\frac{1}{2}\)cosx reaches maximum and minimum value
these points are (0, \(\frac { 1 }{ 2 } \)), (π, –\(\frac { 1 }{ 2 } \))
Question 7.
g(x) = 2 csc 2x
Answer:
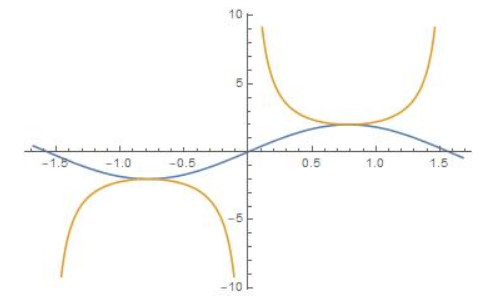
Explanation:
Given that
g(x) = 2 csc 2x
Let’s graph the function f(x) = 2sin2x
Period is π amplitude is 2, midline is x-axis
The x-intercepts are xk = \(\frac { kπ}{ 2 } \), k
Maximum = (\(\frac { π }{ 4 } \) + \(\frac { 2π }{ 3 } \), 2)
Minimum = (-\(\frac { π }{ 4 } \) + \(\frac { 2π }{ 3 } \), -2)
the asymptotes of g(x) are
x = 0
x = \(\frac { π }{ 2 } \)
x = \(\frac { -π }{ 2 } \)
Now let’s plot the points where f(x) = 2sin2x reaches maximum and minimum value
these points are (\(\frac { π }{ 4 } \), 1), (-\(\frac { π }{ 4 } \), -1)
Question 8.
g(x) = 2 sec πx
Answer:
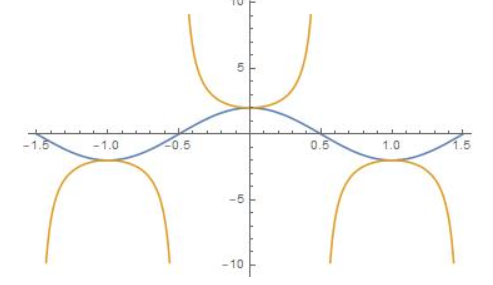
Explanation:
Given that
g(x) = 2 sec πx
Let’s graph the function f(x) = 2cosπx
Period is 2, amplitude is 2, midline is x-axis
The x-intercepts are xk = \(\frac { π1}{ 2 } \) + k
Maximum = (0, 2)
Minimum = (1, -2)
the asymptotes of g(x) are
x = \(\frac { 1 }{ 2 } \)
x = \(\frac { -1 }{ 2 } \)
Now let’s plot the points where f(x) = 2cosπx reaches maximum and minimum value
these points are (0, 2), (1, -2)
Graphing Other Trigonometric Functions 9.5 Exercises
Vocabulary and Core Concept Check
Question 1.
WRITING
Explain why the graphs of the tangent, cotangent, secant, and cosecant functions do not have an amplitude.
Answer:
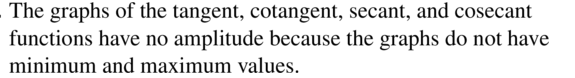
Question 2.
COMPLETE THE SENTENCE
The _______ and _______ functions are undefined for x-values at which sin x = 0.
Answer:
The cosecant and cotangent functions are undefined for x-values at which sin x = 0.
Question 3.
COMPLETE THE SENTENCE
The period of the function y = sec x is _____, and the period of y = cot x is _____.
Answer:
Question 4.
WRITING
Explain how to graph a function of the form y = a sec bx.
Answer:
The period of the function y = secx is 2π and period of y = cotx is π
Monitoring Progress and Modeling with Mathematics
In Exercises 5–12, graph one period of the function. Describe the graph of gas a transformation of the graph of its parent function.
Question 5.
g(x) = 2 tan x
Answer:
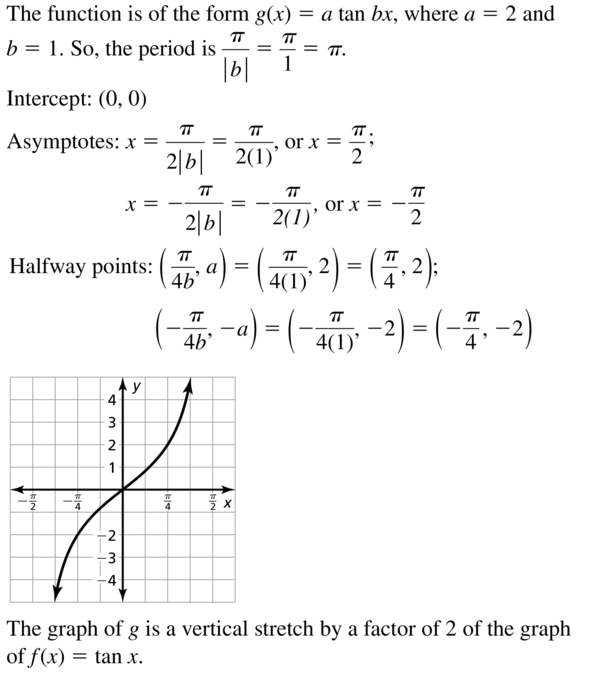
Question 6.
g(x) = 3 tan x
Answer:
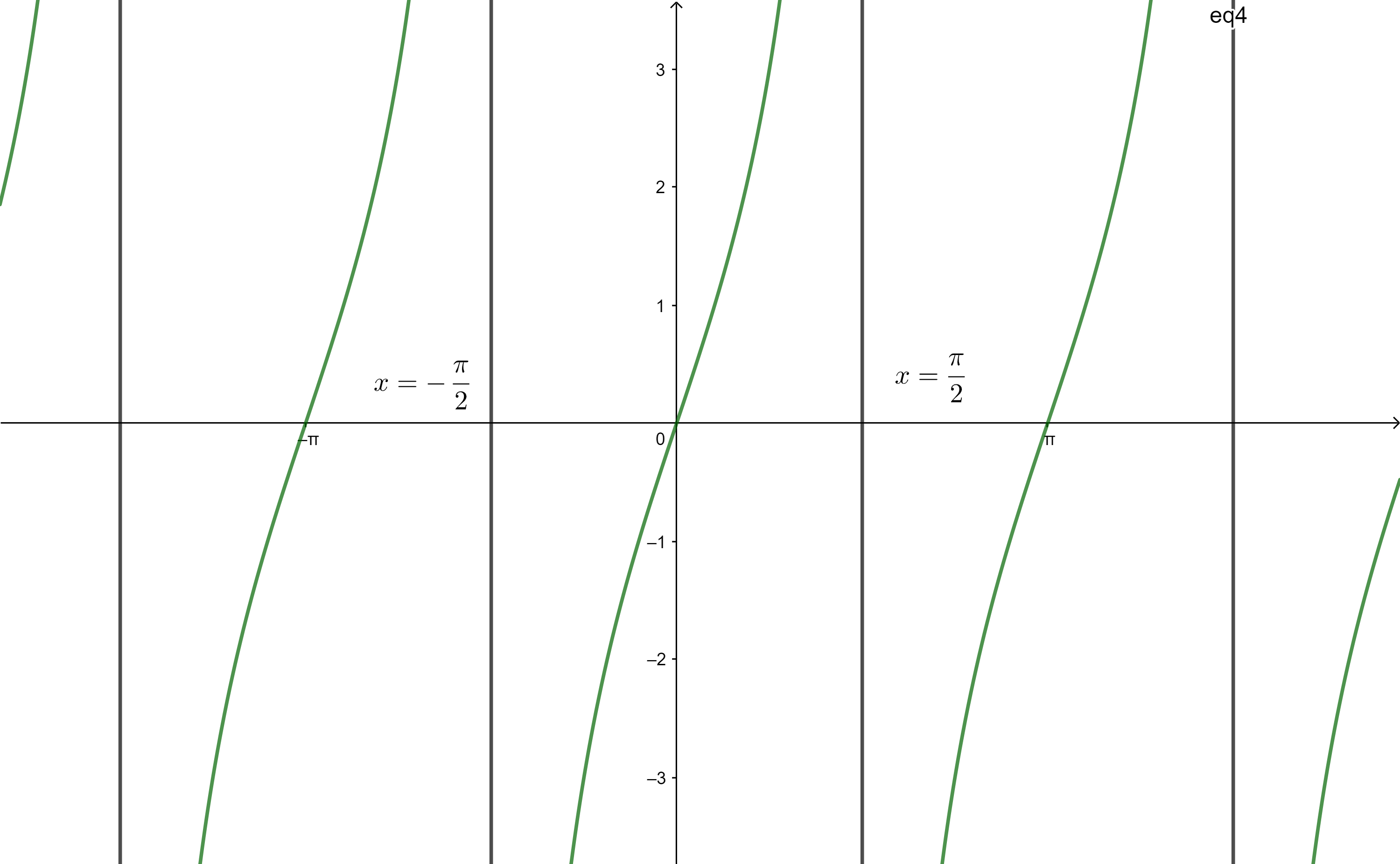
Explanation:
Given that
g(x) = 3 tan x
a = 3, b = 1
Period is π, amplitude is 3
The x-intercepts are (kπ, 0)
The halfway points are (\(\frac { π }{ 4 } \), 3) and (-\(\frac { π }{ 4 } \), -3)
The vertical asymptotoes are
x = \(\frac { π }{ 2 } \)
x = –\(\frac { π }{ 2 } \)
The graph is a vertical strech by a factor of 3 of the graph of f(x) = tanx
Question 7.
g(x) = cot 3x
Answer:
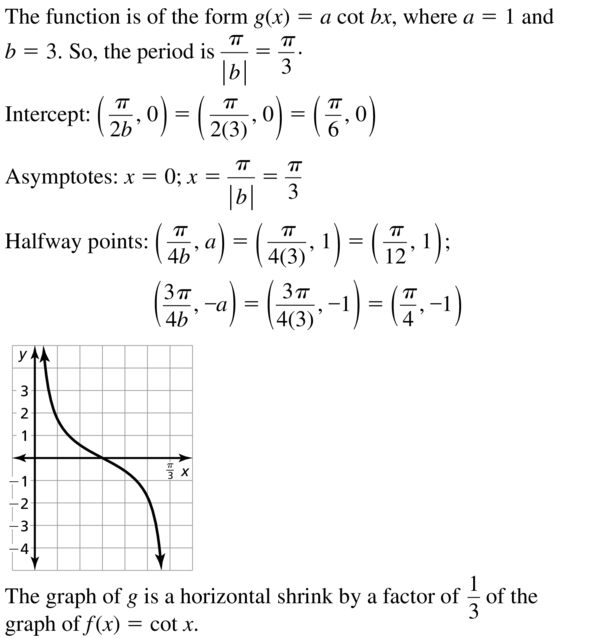
Question 8.
g(x) = cot 2x
Answer:
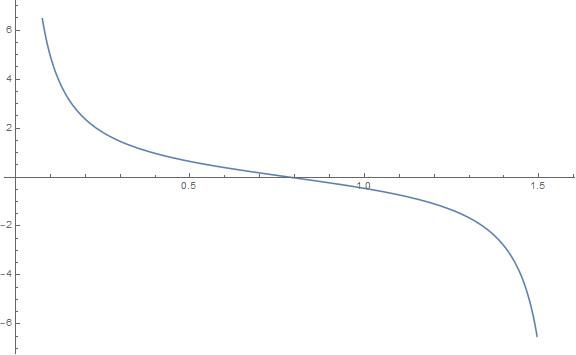
Explanation:
Given that
g(x) = cot 2x
a = 1, b = 2
Period is \(\frac { π }{ 2 } \), amplitude is 1
The x-intercepts are (\(\frac { π }{ 4 } \) + \(\frac { kπ }{ 2 } \), 0)
The halfway points are (\(\frac { π }{ 8 } \), 1) and (\(\frac { 3π }{ 8 } \), -1)
The vertical asymptotoes are
x = 0
x = \(\frac { π }{ 2 } \)
The graph is a vertical strech by a factor of 0.5 of the graph of f(x) = cotx
Question 9.
g(x) = 3 cot \(\frac{1}{4}\)x
Answer:

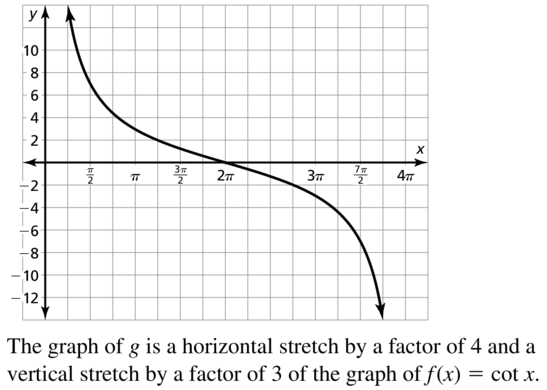
Question 10.
g(x) = 4 cot\(\frac{1}{2}\)x
Answer:
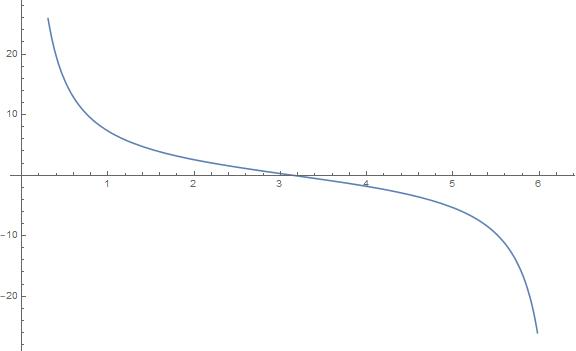
Explanation:
Given that
g(x) = 4 cot\(\frac{1}{2}\)x
a = 4, b = 0.5
Period is 22, amplitude is 4
The x-intercepts are (π + 2kπ, 0)
The halfway points are (\(\frac { π }{ 2 } \), 4) and (\(\frac { 3π }{ 2 } \), -4)
The vertical asymptotoes are
x = 0
x = 2π
The graph is a vertical strech by a factor of 2 of the graph of f(x) = cotx
Question 11.
g(x) = \(\frac{1}{2}\)tan πx
Answer:
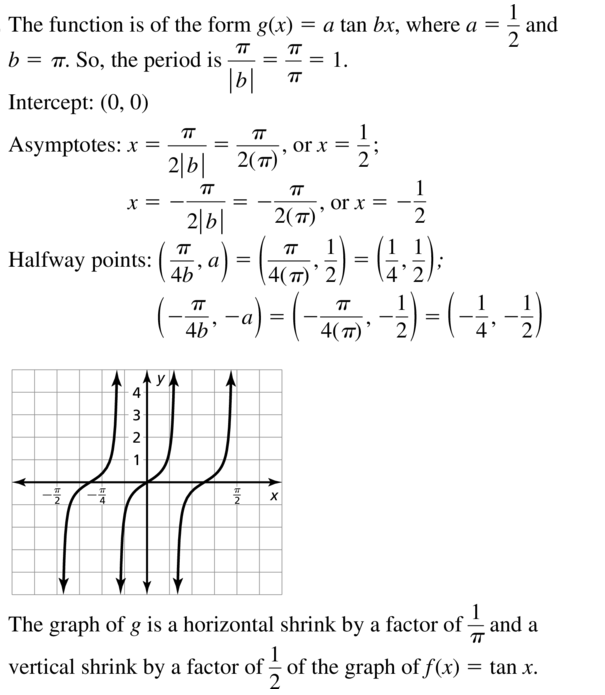
Question 12.
g(x) = \(\frac{1}{3}\) tan 2πx
Answer:
Explanation:
Given that
g(x) = \(\frac{1}{3}\) tan 2πx
a = 1/3, b = 2π
Period is 0.5, amplitude is 1/3
The x-intercepts are (\(\frac { kπ }{ 2 } \), 0)
The halfway points are (\(\frac { 1 }{ 8 } \), \(\frac { 1 }{ 3 } \)) and (-\(\frac { 1 }{ 8 } \), –\(\frac { 1 }{ 3 } \))
The vertical asymptotoes are
x = 0.25
x = -0.25
The graph is a vertical strech by a factor of 1/3 of the graph of f(x) = tanx
Question 13.
ERROR ANALYSIS
Describe and correct the error in finding the period of the function y = cot 3x.

Answer:

Question 14.
ERROR ANALYSIS
Describe and correct the error in describing the transformation of f(x) = tan x represented by g(x) = 2 tan 5x.

Answer:
The graph of g(x) = 2tan(5x) is a vertical strech by a factor of 2 and horizontally shrink by a factor 1/5 of the graph of f(x) = tan x
Question 15.
ANALYZING RELATIONSHIPS
Use the given graph to graph each function.
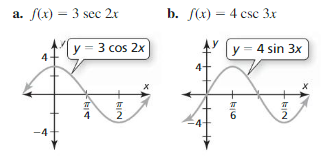
Answer:
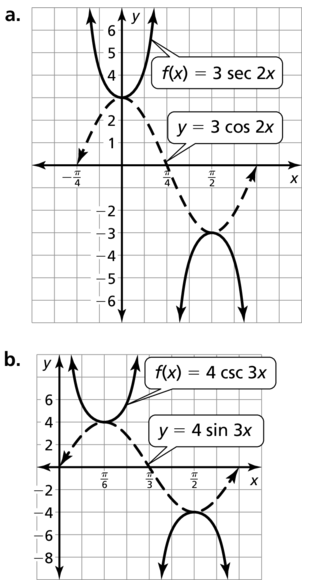
Question 16.
USING EQUATIONS
Which of the following are asymptotes of the graph of y = 3 tan 4x?
A. x = \(\frac{\pi}{8}\)
B. x = \(\frac{\pi}{4}\)
C. x = 0
D. x = −\(\frac{5 \pi}{8}\)
Answer:
x = \(\frac { π }{ 8 } \)
Explanation:
g(x) = 3tan(4x)
The vertical asymptotoes
x = \(\frac { π }{ 8 } \)
xk = \(\frac { π }{ 8 } \) + \(\frac { kπ }{ 4 } \)
In Exercises 17–24, graph one period of the function. Describe the graph of gas a transformation of the graph of its parent function.
Question 17.
g(x) = 3 csc x
Answer:
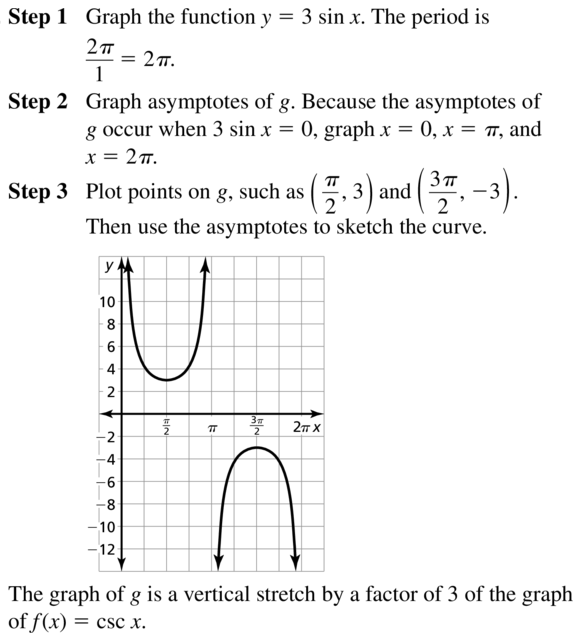
Question 18.
g(x) = 2 csc x
Answer:
Explanation:
g(x) = 2 csc x
Let’s graph the function f(x) = 2sinx
Period is 2π, amplitude is 2, midline is x-axis
The x-intercepts are xk = \(\frac { kπ}{ 2 } \), k
Maximum = (\(\frac { π }{ 2 } \) + 2kπ, 2)
Minimum = (\(\frac { 3π }{ 2 } \) + 2kπ, -2)
the asymptotes of g(x) are
x = 0
x = π
x = -π
Now let’s plot the points where f(x) = 2sinx reaches maximum and minimum value
these points are (\(\frac { π }{ 2 } \), 2), (-\(\frac { π }{ 2 } \), -2)
Question 19.
g(x) = sec 4x
Answer:

Question 20.
g(x) = sec 3x
Answer:
Explanation:
g(x) = sec 3x
Let’s graph the function f(x) = cos(3x)
Period is \(\frac { 2π }{ 3 } \), amplitude is 1, midline is x-axis
The x-intercepts are xk = \(\frac { π }{ 6 } \) + \(\frac { 2kπ }{ 3 } \)
Maximum = (0, 1)
Minimum = (\(\frac { π }{ 3 } \), -1)
the asymptotes of g(x) are
x = \(\frac { -π }{ 6 } \)
x = \(\frac { π }{ 6 } \)
Now let’s plot the points where f(x) = cos(3x) reaches maximum and minimum value
these points are (0, 1), (\(\frac { π }{ 6 } \), -1)
Question 21.
g(x) = \(\frac{1}{2}\)sec πx
Answer:
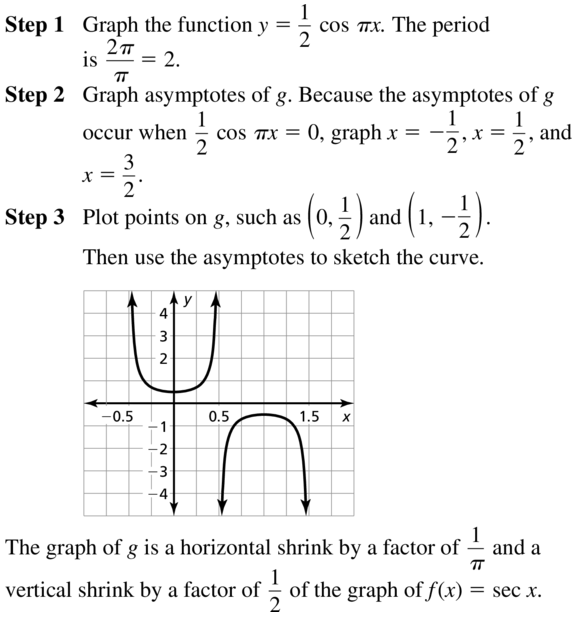
Question 22.
g(x) = \(\frac{1}{4}\) sec 2πx
Answer:
Explanation:
g(x) = \(\frac{1}{4}\) sec 2πx
Let’s graph the function f(x) = \(\frac{1}{4}\) cos 2πx. The graph of the function f(x) represent a vertically shrink by a factor 0.25 followed by a horizontally shrink by a fcator \(\frac { 1 }{ 2π } \) of the function cosx.
Period is 1, amplitude is \(\frac { 1 }{ 4 } \), midline is x-axis
The x-intercepts are xk = \(\frac { 1 }{ 4 } \) + k
Maximum = (0, \(\frac { 1 }{ 4 } \))
Minimum = (\(\frac { 1 }{ 2 } \), –\(\frac { 1 }{ 4 } \))
the asymptotes of g(x) are
x = \(\frac { 1 }{ 4 } \)
x = –\(\frac { 1 }{ 4 } \)
Now let’s plot the points where f(x) = \(\frac{1}{4}\) cos 2πx reaches maximum and minimum value
these points are (0, \(\frac { 1 }{ 4 } \)), (\(\frac { 1 }{ 2 } \), –\(\frac { 1 }{ 4 } \))
Question 23.
g(x) = csc \(\frac{\pi}{2}\)x
Answer:
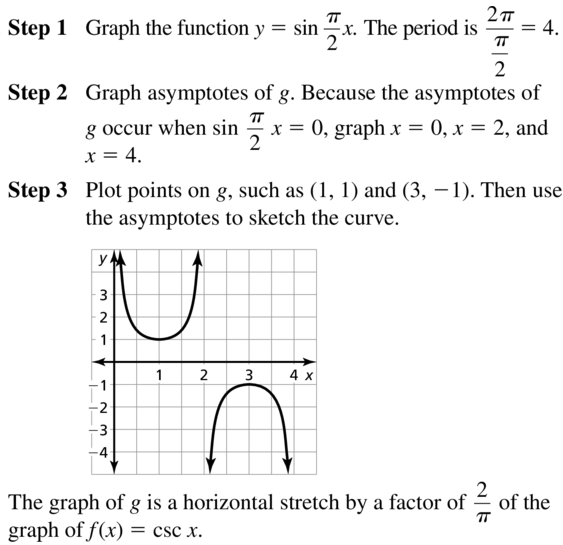
Question 24.
g(x) = csc \(\frac{\pi}{4}\)x
Answer:

Explanation:
g(x) = csc \(\frac{\pi}{4}\)x
Let’s graph the function f(x) = sin\(\frac{\pi}{4}\)x. The graph of the function f(x) represent a horizontaly stretch shrink by a factor \(\frac { 4 }{ π } \) of the function sinx.
Period is 8, amplitude is 1, midline is x-axis
The x-intercepts are xk = 4k
Maximum = (2, 1)
Minimum = (6, -1)
the asymptotes of g(x) are
x = 0
x = 4
x = -4
Now let’s plot the points where f(x) = sin\(\frac{\pi}{4}\)x reaches maximum and minimum value
these points are (2, 1), (6, -1)
ATTENDING TO PRECISION In Exercises 25–28, use the graph to write a function of the form y = a tan bx.
Question 25.
Answer:
Question 26.
Answer:
Amplitude a = \(\frac { 1 }{ 2 } \), b = 1
So, the function y = \(\frac { 1 }{ 2 } \) tanx has a given graph.
Question 27.
Answer:
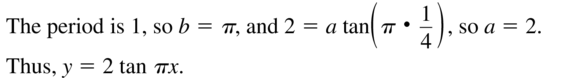
Question 28.

Answer:
Amplitude a = 5, b = 2
So, the function y = 5tan(2x) has a given graph.
USING STRUCTURE In Exercises 29–34, match the equation with the correct graph. Explain your reasoning.
Question 29.
g(x) = 4 tan x
Answer:

Question 30.
g(x) = 4 cot x
Answer:
The graph of the function g(x) matches the graph denoted with C.
Explanation:
Let’s consider the function g(x) = 4 cotx
The graph of the function g(x) will have asymptotoes x = 0, x = π, x-intersect is in the point (\(\frac { π }{ 2 } \), 0) and the graph will represent vertically strech by a factor 4 of its parent function f(x) = cotx. The graph of the function g(x) matches with the graph denoted with C.
Question 31.
g(x) = 4 csc πx
Answer:
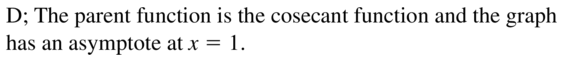
Question 32.
g(x) = 4 sec πx
Answer:
The graph of the function g(x) matches the graph denoted with F.
Question 33.
g(x) = sec 2x
Answer:

Question 34.
g(x) = csc 2x
Answer:
The graph of the function g(x) matches with the graph denoted with E.
Question 35.
WRITING
Explain why there is more than one tangent function whose graph passes through the origin and has asymptotes at x = −π and x = π.
Answer:

Question 36.
USING EQUATIONS
Graph one period of each function. Describe the transformation of the graph of its parent function.
a. g(x) = sec x + 3
b. g(x) = csc x − 2
c. g(x) = cot(x − π)
d. g(x) = −tan x
Answer:
a. The graph of function secx + 3
b. The graph of the function cosecx – 2
c. The graph of the function cot(x – π)
d. The graph of the function -tanx
Explanation:
a. Let’s consider g(x) = secx + 3
The graph of the function g(x) will represent the graph of sec x moved 3 units up. Hence, the period will be the same as the period of the function sec x which is 2π.
b. Let’s consider g(x) = cosecx – 2
The graph of the function g(x) will represent the graph of cosec x moved 2 units up. Hence, the period will be the same as the period of the function sec x which is 2π.
c. Let’s consider g(x) = cot(x – π)
The graph of the function g(x) will represent the graph of cot x horizontally moved π units right. Hence, the period will be the same as a period of the function cot x which is π.
d. Let’s consider g(x) = -tanx
The graph of the function g(x) will represent the graph of tan x reflected about the x-axis. Hence, the period will be the same as a period of the function tan x which is π.
WRITING EQUATIONS In Exercises 37–40, write a rule for g that represents the indicated transformation of the graph of f.
Question 37.
f(x) = cot 2x; translation 3 units up and \(\frac{\pi}{2}\) units left
Answer:
Question 38.
f(x) = 2 tan x; translation π units right, followed by a horizontal shrink by a factor of \(\frac{1}{3}\)
Answer:
The rule for the transformation is g(x) = 2tan(3x – π)
Question 39.
f(x) = 5 sec (x − π); translation 2 units down, followed by a reflection in the x-axis
Answer:
![]()
Question 40.
f(x) = 4 csc x; vertical stretch by a factor of 2 and a reflection in the x-axis
Answer:
The rule for the transformation is g(x) = -8 cscx
Question 41.
MULTIPLE REPRESENTATIONS
Which function has a greater local maximum value? Which has a greater local minimum value? Explain.
Answer:

Question 42.
ANALYZING RELATIONSHIPS
Order the functions from the least average rate of change to the greatest average rate of change over the interval −\(\frac{\pi}{4}\) < x < \(\frac{\pi}{4}\).
Answer:
rD < rB < rC < rA
Explanation:
The average rate r = \(\frac { f(b) – f(a) }{ b – a } \)
A. x = ±\(\frac { π }{ 4 } \)
f(\(\frac { π }{ 4 } \)) = 2
f(-\(\frac { π }{ 4 } \)) = -2
The avergae rate on the interval (-\(\frac { π }{ 4 } \), \(\frac { π }{ 4 } \)) is
rA = \(\frac { f(π/4) – f(-π/4) }{ π/4 + π/4 } \)
= 2.546
B. x = ±\(\frac { π }{ 4 } \)
f(\(\frac { π }{ 4 } \)) = -1
f(-\(\frac { π }{ 4 } \)) = 1
The avergae rate on the interval (-latex]\frac { π }{ 4 } [/latex], latex]\frac { π }{ 4 } [/latex]) is
rB = \(\frac { f(π/4) – f(-π/4 }{ π/4 + π/4 } \)
= -1.27
C. x = ±\(\frac { π }{ 4 } \)
f(\(\frac { π }{ 4 } \)) = 0.5
f(-\(\frac { π }{ 4 } \)) = -0.5
The avergae rate on the interval (-latex]\frac { π }{ 4 } [/latex], latex]\frac { π }{ 4 } [/latex]) is
rC = \(\frac { f(π/4) – f(-π/4 }{ π/4 + π/4 } \)
= 0.637
D. x = ±\(\frac { π }{ 4 } \)
f(\(\frac { π }{ 4 } \)) = -2
f(-\(\frac { π }{ 4 } \)) = 2
The avergae rate on the interval (-latex]\frac { π }{ 4 } [/latex], latex]\frac { π }{ 4 } [/latex]) is
rD = \(\frac { f(π/4) – f(-π/4 }{ π/4 + π/4 } \)
= -2.546
From the results rD < rB < rC < rA
Question 43.
REASONING
You are standing on a bridge 140 feet above the ground. You look down at a car traveling away from the underpass. The distance d (in feet) the car is from the base of the bridge can be modeled by d= 140 tan θ. Graph the function. Describe what happens to θ as d increases
Answer:
Question 44.
USING TOOLS
You use a video camera to pan up the Statue of Liberty. The height h (in feet) of the part of the Statue of Liberty that can be seen through your video camera after time t (in seconds) can be modeled by h= 100 tan \(\frac{\pi}{36}\)t. Graph the function using a graphing calculator. What viewing window did you use? Explain.
Answer:
It would take around 15 seconds to span the statue of liberty.
Explanation:
h(t) = 100 tan \(\frac{\pi}{36}\)t
The graph of h(t) represent a vertical strech by a factor of 2, followed by a horizontal stretch by a factor \(\frac { 36 }{ π } \) of the graph of its parent function f(t) = tan t. The graph of h(t) is
The statue of liberty is about 305 ft tall. From the graph, we can say that it would take around 15 seconds to span the statue of liberty, because in 15 seconds we already can span around 373 ft
Question 45.
MODELING WITH MATHEMATICS
You are standing 120 feet from the base of a 260-foot building. You watch your friend go down the side of the building in a glass elevator.

a. Write an equation that gives the distance d (in feet) your friend is from the top of the building as a function of the angle of elevation θ.
b. Graph the function found in part (a). Explain how the graph relates to this situation.
Answer:
Question 46.
MODELING WITH MATHEMATICS
You are standing 300 feet from the base of a 200-foot cliff. Your friend is rappelling down the cliff.
a. Write an equation that gives the distance d(in feet) your friend is from the top of the cliff as a function of the angle of elevation θ.
b. Graph the function found in part (a).
c. Use a graphing calculator to determine the angle of elevation when your friend has rappelled halfway down the cliff.

Answer:
a. The function for the distance d(θ) = 200 – 300 tanθ
b. 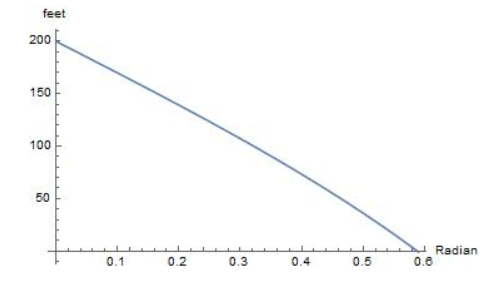
c. θ = 18.4°
Explanation:
a. tan θ = \(\frac { 200 – d }{ 300 } \)
300 tanθ = 200 – d
d = 200 – 300 tanθ
d(θ) = 200 – 300 tanθ
c. From the graph, when your friend has reppelled halfway down the cliff, the angle of elevation is θ = 0.32 radians or θ = 18.4°
Question 47.
MAKING AN ARGUMENT
Your friend states that it is not possible to write a cosecant function that has the same graph as y = sec x. Is your friend correct? Explain your reasoning.
Answer:

Question 48.
HOW DO YOU SEE IT?
Use the graph to answer each question.
a. What is the period of the graph?
b. What is the range of the function?
c. Is the function of the form f(x) = a csc bx or f(x) = a sec bx? Explain.
Answer:
a. The period = 2(-2) = 4
b. The range of the function is (-∞, -2] U [2, ∞)
c. f(x) = a cosbx
Question 49.
ABSTRACT REASONING
Rewrite a sec bx in terms of cos bx. Use your results to explain the relationship between the local maximums and minimums of the cosine and secant functions.
Answer:
Question 50.
THOUGHT PROVOKING
A trigonometric equation that is true for all values of the variable for which both sides of the equation are defined is called a trigonometric identity.Use a graphing calculator to graph the function
y = \(\frac{1}{2}\)(tan \(\frac{x}{2}\) + cot \(\frac{x}{2}\)) .
Use your graph to write a trigonometric identity involving this function. Explain your reasoning.
Answer:
\(\frac { 1 }{ 2 } \)(cot \(\frac { x }{ 2 } \) + tan \(\frac { x }{ 2 } \)) = cosec x
Explanation:
The graph of the function y = \(\frac{1}{2}\)(tan \(\frac{x}{2}\) + cot \(\frac{x}{2}\)) is
\(\frac{1}{2}\)(tan \(\frac{x}{2}\) + cot \(\frac{x}{2}\)) = cosecx
Question 51.
CRITICAL THINKING
Find a tangent function whose graph intersects the graph of y = 2 + 2 sin x only at minimum points of the sine function.
Answer:
Maintaining Mathematical Proficiency
Write a cubic function whose graph passes through the given points.
Question 52.
(−1, 0), (1, 0), (3, 0), (0, 3)
Answer:
The cubic function is f(x) = x³ – 3x² – x + 3
Explanation:
Let’s find the cubic function f(x) that passes through the points (-1, 0), (1, 0), (3, 0), (0, 3)
The point where y-coordinate is equal to 0 means that x-coordinate is 0 of the cubic function. Since 1, -1, 3 will be zeros of f(x)
f(x) = a(x – 1)(x + 1)(x – 3)
Now, from the point (0, 3)
f(0) = 3
a(0 – 1)(0 + 1)(0 – 3) = 3
3a = 3
a = 1
Hence the cubic function is (x – 1)(x + 1)(x – 3)
Question 53.
(−2, 0), (1, 0), (3, 0), (0, −6)
Answer:

Question 54.
(−1, 0), (2, 0), (3, 0), (1, −2)
Answer:
The cubic function is f(x) = –\(\frac { 1 }{ 2 } \)x³ + 2x² – \(\frac { 1 }{ 2 } \)x – 3
Explanation:
Let’s find the cubic function f(x) that passes through the points (−1, 0), (2, 0), (3, 0), (1, −2)
The point where y-coordinate is equal to 0 means that x-coordinate is 0 of the cubic function. Since -1, 2, 3 will be zeros of f(x)
f(x) = a(x – 1)(x + 1)(x – 3)
Now, from the point (1, -2)
f(1) = -2
a(1 + 1)(1 – 2)(1 – 3) = -2
4a = -2
a = -0.5
Hence the cubic function is -0.5(x – 1)(x + 1)(x – 3)
Question 55.
(−3, 0), (−1, 0), (3, 0), (−2, 1)
Answer:

Find the amplitude and period of the graph of the function.
Question 56.
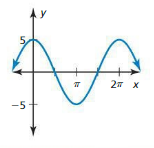
Answer:
The period is 2π, the amplitude is 5
Question 57.
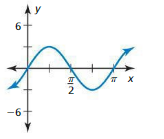
Answer:
![]()
Question 58.

Answer:
The period is 8π, the amplitude is 1
Lesson 9.6 Modeling with Trigonometric Functions
Essential Question What are the characteristics of the real-life problems that can be modeled by trigonometric functions?
EXPLORATION 1
Modeling Electric Currents
Work with a partner. Find a sine function that models the electric current shown in each oscilloscope screen. State the amplitude and period of the graph.

Communicate Your Answer
Question 2.
What are the characteristics of the real-life problems that can be modeled by trigonometric functions?
Answer:
Question 3.
Use the Internet or some other reference to find examples of real-life situations that can be modeled by trigonometric functions.
Answer:
Monitoring Progress
Question 1.
WHAT IF?
In Example 1, how would the function change when the audiometer produced a pure tone with a frequency of 1000 hertz?
Answer:
Explanation:
Let’s suppose that the audiometer produced a pure tone with a frequency of 100 hz. The maximum pressure is 2. so a = 2
f = \(\frac { 1 }{ T } \)
1000 = \(\frac { 1 }{ T } \)
T = \(\frac { 1 }{ 1000 } \)
From the formula
\(\frac { 1 }{ 1000 } \) = \(\frac { 2π }{ b } \)
b = 2000π
The pressure P(x) = 2sin2000πx
x-intercepts (\(\frac { 1 }{ 2000 } \), 0)
Maximum = (\(\frac { 1 }{ 4000 } \), 2)
Minimum = (\(\frac { 3 }{ 1000 } \), -2)
Write a function for the sinusoid.
Question 2.
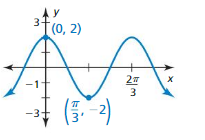
Answer:
y = 2 cos 3x
Explanation:
Let’s determine the form of f(x)
y = asin(b(x – h)) + k, y = a cos(b(x-h)) + k
The maximum and minimum values are fmax = 2, fmin = -2
k = 0
period = \(\frac { 2π }{ 3 } \)
Amplitude |a| = 2
So, y = 2cos(3(x-0)) + 0 = 2cos3x
Question 3.
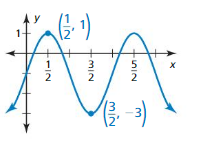
Answer:
y = 2sinπx – 1
Explanation:
Let’s determine the form of f(x)
y = asin(b(x – h)) + k, y = a cos(b(x-h)) + k
The maximum and minimum values are fmax = 1, fmin = -3
k = -1
period = \(\frac { 2π }{ π } \) = 2
Amplitude |a| = 2
So, y = 2sin(π(x-0)) + (-1) = 2sinπx – 1
Question 4.
WHAT IF?
Describe how the model in Example 3 changes when the lowest point of a rope is 5 inches above the ground and the highest point is 70 inches above the ground.
Answer:
y = 32.5sin4πt + 37.5
Explanation:
Let’s determine the form of f(x)
y = asin(b(x – h)) + k, y = a cos(b(x-h)) + k
The maximum and minimum values are fmax = 70, fmin = 5
k = 37.5
period = 0.5
Amplitude |a| = 32.5
So, y = -32.5sin(4π(t-0)) + 37.5 = 32.5sin4πt + 37.5
Question 5.
The table shows the average daily temperature T (in degrees Fahrenheit) for a city each month, where m = 1 represents January. Write a model that gives T as a function of m and interpret the period of its graph.

Answer:
The model is N(t) = 21.63 sin(0.524x – 2.248) + 51.667
Explanation:
The scatter plot of the data is

The scatter plot appears sinusoidal. So perform a sinusoidal regression.
The regression gives
SinReg
D = a sin(ax + b) + d
a = 21.63
b = 0.524
c = -2.248
d = 51.667
The model is N(t) = 21.63 sin(0.524x – 2.248) + 51.667
Period T = 12
The period of the model represents the amount of time to repeat its cycles which is 12 months. Plot the function N(t) on the scatter plot
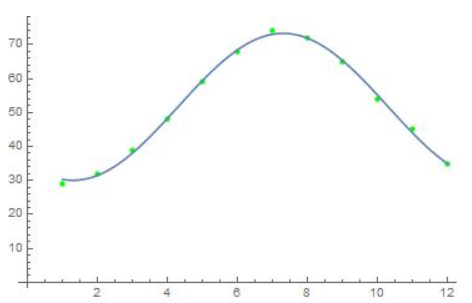
Modeling with Trigonometric Functions 9.6 Exercises
Vocabulary and Core Concept Check
Question 1.
COMPLETE THE SENTENCE
Graphs of sine and cosine functions are called __________.
Answer:
![]()
Question 2.
WRITING
Describe how to find the frequency of the function whose graph is shown.

Answer:
Frequency = \(\frac { 1 }{ Period } \) = 3
Explanation:
Frequency = \(\frac { 1 }{ Period } \)
Period = \(\frac { 1 }{ 3 } \)
Frequency = \(\frac { 1 }{ [latex]\frac { 1 }{ 3 } \) } [/latex]
= 3
Monitoring Progress and Modeling with Mathematics
In Exercises 3–10, find the frequency of the function.
Question 3.
y = sin x
Answer:
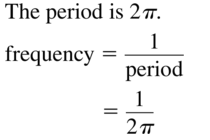
Question 4.
y = sin 3x
Answer:
Period is \(\frac { 2π }{ 3 } \)
Freuency = \(\frac { 1 }{ 2π/3 } \)
= \(\frac { 3 }{ 2π } \)
Question 5.
y = cos 4x + 2
Answer:

Question 6.
y =−cos 2x
Answer:
Period = π
Frequency = \(\frac { 1 }{ π } \)
Question 7.
y = sin 3πx
Answer:

Question 8.
y = cos \(\frac{\pi x}{4}\)
Answer:
Period is 8
Frequency = \(\frac { 1 }{ 8 } \)
Question 9.
y = \(\frac{1}{2}\) cos 0.75x − 8
Answer:

Question 10.
y = 3 sin 0.2x + 6
Answer:
Period = 10π
Frequency = \(\frac { 1 }{ 10π } \)
Question 11.
MODELING WITH MATHEMATICS
The lowest frequency of sounds that can be heard by humans is 20 hertz. The maximum pressure P produced from a sound with a frequency of 20 hertz is 0.02 millipascal. Write and graph a sine model that gives the pressure P as a function of the time t(in seconds).
Answer:


Question 12.
MODELING WITH MATHEMATICS
A middle-A tuning fork vibrates with a frequency f of 440 hertz (cycles per second). You strike a middle-A tuning fork with a force that produces a maximum pressure of 5 pascals. Write and graph a sine model that gives the pressure Pas a function of the time t (in seconds).

Answer:
The sine model is P(t) = 5 sin(880πt)
Explanation:
From the given data, a middle A tuning fork is vibrates with a frequency of 440 hz. You strike a middle A tuning fork with a force that produces a maximum pressure of 5 pascals, so a = 5
440 = \(\frac { 1 }{ Period } \)
Period = \(\frac { 1 }{ 440} \)
\(\frac { 1 }{ 440} \) = \(\frac { 2π }{ b } \)
b = 880π
the sine model is P(t) = 5 sin(880πt)
In Exercises 13–16, write a function for the sinusoid.
Question 13.

Answer:

Question 14.

Answer:
y = 5 cos4x
Explanation:
Let’s determine the form of f(x)
y = asin(b(x – h)) + k, y = a cos(b(x-h)) + k
The maximum and minimum values are fmax = 5, fmin = -5
k = 0
period = \(\frac { π }{ 2 } \)
Amplitude |a| = 5
So, y = 5 cos(4(x – 0)) + 0 = 5 cos4x
Question 15.
Answer:

Question 16.

Answer:
y = -sin πx – 2
Explanation:
Let’s determine the form of f(x)
y = asin(b(x – h)) + k, y = a cos(b(x-h)) + k
The maximum and minimum values are fmax = -1, fmin = -3
k = -2
period = 2
Amplitude |a| = 1
So, y = -sin(π(x – 0)) + (-2) = -sin πx – 2
Question 17.
ERROR ANALYSIS
Describe and correct the error in finding the amplitude of a sinusoid with a maximum point at (2, 10) and a minimum point at (4, −6).
Answer:
Question 18.
ERROR ANALYSIS
Describe and correct the error in finding the vertical shift of a sinusoid with a maximum point at (3, −2) and a minimum point at (7, −8).

Answer:
k = \(\frac { minimum value + maximum value }{ 2 } \)
= \(\frac { -2 + (-8) }{ 2 } \)
= -5
Question 19.
MODELING WITH MATHEMATICS
One of the largest sewing machines in the world has a flywheel (which turns as the machine sews) that is 5 feet in diameter. The highest point of the handle at the edge of the flywheel is 9 feet above the ground, and the lowest point is 4 feet. The wheel makes a complete turn every 2 seconds. Write a model for the height h(in feet) of the handle as a function of the time t(in seconds) given that the handle is at its lowest point when t = 0.
Answer:

Question 20.
MODELING WITH MATHEMATICS
The Great LaxeyWheel, located on the Isle of Man, is the largest working water wheel in the world. The highest point of a bucket on the wheel is 70.5 feet above the viewing platform, and the lowest point is 2 feet below the viewing platform. The wheel makes a complete turn every 24 seconds. Write a model for the height h(in feet) of the bucket as a function of time t (in seconds) given that the bucket is at its lowest point when t = 0.

Answer:
y = –\(\frac { 72.5 }{ 2 } \)cos(\(\frac { π }{ 12 } \)t) + 34.25
Explanation:
Let’s determine the form of f(x)
y = asin(b(x – h)) + k, y = a cos(b(x-h)) + k
The maximum and minimum values are fmax = 70.5, fmin = -2
k = \(\frac { 68.5 }{ 2 } \)
period = 24
Amplitude |a| = \(\frac { 72.5 }{ 2 } \)
So, y = –\(\frac { 72.5 }{ 2 } \)cos(\(\frac { π }{ 12 } \)(t – 0)) + \(\frac { 68.5 }{ 2 } \) = –\(\frac { 72.5 }{ 2 } \)cos(\(\frac { π }{ 12 } \)t) + 34.25
USING TOOLS In Exercises 21 and 22, the time t is measured in months, where t = 1 represents January. Write a model that gives the average monthly high temperature D as a function of t and interpret the period of the graph.
Question 21.
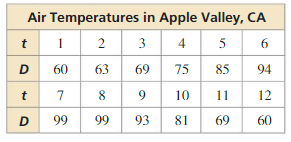
Answer:
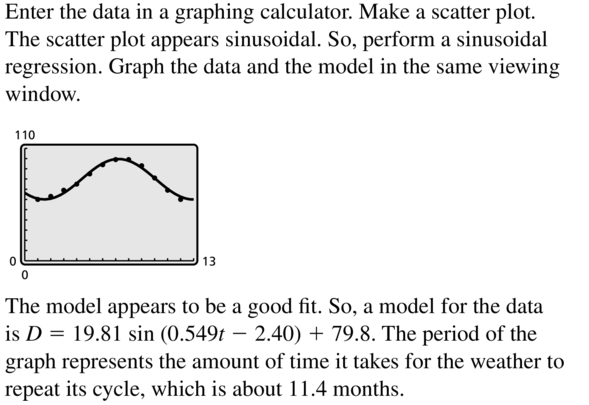
Question 22.
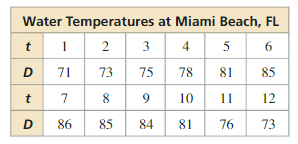
Answer:
The model is D(t) = 7.380 sin(0.498x – 2.052) + 78.640
Explanation:
The scatter plot of the data is
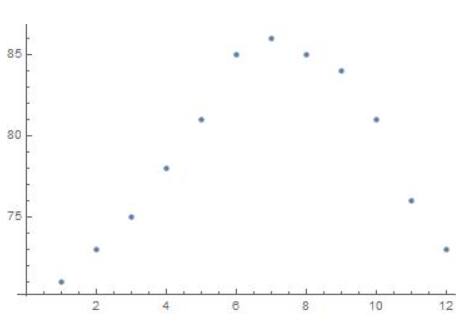
The scatter plot appears sinusoidal. So perform a sinusoidal regression.
The regression gives
SinReg
D = a sin(ax + b) + d
a = 7.380
b = 0.498
c = -2.052
d = 78.640
The model is D(t) = 7.380 sin(0.498x – 2.052) + 78.640
Period T = 12.6
The period of the model represents the amount of time to repeat its cycles which is 12.6 months. Plot the function D(t) on the scatter plot
Question 23.
MODELING WITH MATHEMATICS
A circuit has an alternating voltage of 100 volts that peaks every 0.5 second. Write a sinusoidal model for the voltage Vas a function of the time t (in seconds).
Answer:

Question 24.
MULTIPLE REPRESENTATIONS
The graph shows the average daily temperature of Lexington, Kentucky. The average daily temperature of Louisville, Kentucky, is modeled by y =−22 cos \(\frac{\pi}{6}\)t + 57, where y is the temperature (in degrees Fahrenheit) and t is the number of months since January 1. Which city has the greater average daily temperature? Explain.
Answer:
Louisville
Explanation:
The average daily temperature in Louisville
The two functions have the same period and horizontal shift, but different amplitudes and vertical shift. The city with greater average daily temperature is Louisville.
Question 25.
USING TOOLS
The table shows the numbers of employees N (in thousands) at a sporting goods company each year for 11 years. The time t is measured in years, with t = 1 representing the first year.
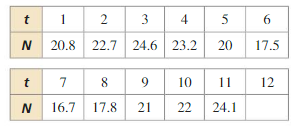
a. Use sinusoidal regression to find a model that gives N as a function of t.
b. Predict the number of employees at the company in the 12th year.
Answer:

Question 26.
THOUGHT PROVOKING
The figure shows a tangent line drawn to the graph of the function y = sin x. At several points on the graph, draw a tangent line to the graph and estimate its slope. Then plot the points (x, m), where m is the slope of the tangent line. What can you conclude?
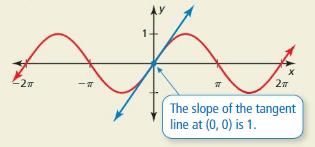
Answer:
The slope of the graph of the function y = sinx can be represented with the function cosx.
Explanation:
The tangent line in the point (0, 0) of the function y = sinx is y = x and the slope is 1. Now, the tangent line of the function y = sinx in the point (\(\frac { π }{ 2 } \), 1) will be
y = 1 with slope equal to 0.
In point (π, 0), the tangent line is
y = -x + π, with slope equal to -1.
In the point (\(\frac { 3π }{ 2 } \), 0), the tangent line is
y = -1 with slope equal to 0
In the point (2π, 0), the tangent line is
y = x + 2π with slope equal to 1
In the point (\(\frac { -π }{ 2 } \), 1), the tangent line is
y = -1 with slope equal to 0
In the point (-π, 0), the tangent line is
y = -x – 2π with slope equal to -1
In the point (\(\frac { -3π }{ 2 } \), 0), the tangent line is
y = 1 with slope equal to 0
In the point (-2π, 0), the tangent line is
y = x – 2π with slope equal to 1
Question 27.
REASONING
Determine whether you would use a sine or cosine function to model each sinusoid with the y-intercept described. Explain your reasoning.
a. The y-intercept occurs at the maximum value of the function.
b. The y-intercept occurs at the minimum value of the function.
c. The y-intercept occurs halfway between the maximum and minimum values of the function.
Answer:

Question 28.
HOW DO YOU SEE IT?
What is the frequency of the function whose graph is shown? Explain.
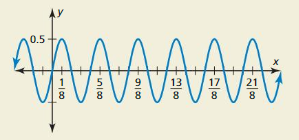
Answer:
Frequency = \(\frac { 1 }{ Period } \)
Period = 0.5
Frequency = \(\frac { 1 }{ 0.5 } \) = 2
Question 29.
USING STRUCTURE
During one cycle, a sinusoid has a minimum at (\(\frac{\pi}{2}\), 3 ) and a maximum at (\(\frac{\pi}{4}\), 8 ). Write a sine function and a cosine function for the sinusoid. Use a graphing calculator to verify that your answers are correct.
Answer:

Question 30.
MAKING AN ARGUMENT
Your friend claims that a function with a frequency of 2 has a greater period than a function with a frequency of \(\frac{1}{2}\). Is your friend correct? Explain your reasoning.
Answer:
My friend is not correct
Explanation:
Frequency of f(x) = \(\frac { 1 }{ Period of f(x) } \)
2 = \(\frac { 1 }{ Tf } \)
Tf = 0.5
Frequency of g(x) = \(\frac { 1 }{ Period of g(x) } \)
0.5 = \(\frac { 1 }{ Tg } \)
Tg = 2
The function with frequency 2 has a smaller period than the function with frequency 1/2.
Question 31.
PROBLEM SOLVING
The low tide at a port is 3.5 feet and occurs at midnight. After 6 hours, the port is at high tide, which is 16.5 feet.
a. Write a sinusoidal model that gives the tide depth d(in feet) as a function of the time t(in hours). Let t = 0 represent midnight.
b. Find all the times when low and high tides occur in a 24-hour period.
c. Explain how the graph of the function you wrote in part (a) is related to a graph that shows the tide depth d at the port t hours after 3:00 A.M.
Answer:

Maintaining Mathematical Proficiency
Simplify the expression.
Question 32.
\(\frac{17}{\sqrt{2}}\)
Answer:
\(\frac{17}{\sqrt{2}}\) = \(\frac { 17√2 }{ 2 } \)
Explanation:
\(\frac{17}{\sqrt{2}}\) = \(\frac{17}{\sqrt{2}}\) x \(\frac { √2 }{ √2 } \)
= \(\frac { 17√2 }{ 2 } \)
Question 33.
\(\frac{3}{\sqrt{6}-2}\)
Answer:
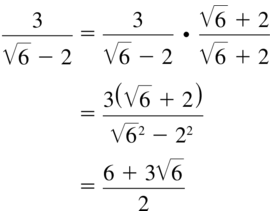
Question 34.
\(\frac{8}{\sqrt{10}+3}\)
Answer:
\(\frac{8}{\sqrt{10}+3}\) = 8√10 – 24
Explanation:
\(\frac{8}{\sqrt{10}+3}\) = \(\frac{8}{\sqrt{10}+3}\) x \(\frac { √10 – 3 }{ √10 – 3 } \)
= \(\frac { 8(√10 – 3) }{ 10 – 9 } \)
= 8√10 – 24
Question 35.
\(\frac{13}{\sqrt{3}+\sqrt{11}}\)
Answer:
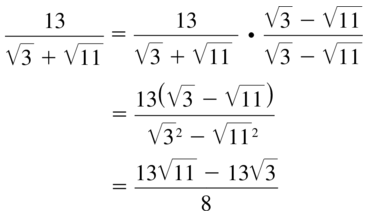
Expand the logarithmic expression.
Question 36.
log8\(\frac{x}{7}\)
Answer:
log8\(\frac{x}{7}\) = log8x – log87
Question 37.
ln 2x
Answer:
![]()
Question 38.
log3 5x3
Answer:
log3 5x3 = log3 5 + 3log3 x
Question 39.
ln \(\frac{4 x^{6}}{y}\)
Answer:

Lesson 9.7 Using Trigonometric Identities
Essential Question How can you verify a trigonometric identity?
EXPLORATION 1
Writing a Trigonometric Identity
Work with a partner. In the figure, the point (x, y) is on a circle of radius c with center at the origin.
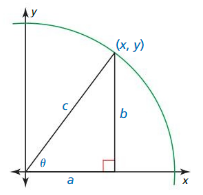
a. Write an equation that relates a, b, and c.
b. Write expressions for the sine and cosine ratios of angle θ.
c. Use the results from parts (a) and (b) to find the sum of sin2θ and cos2θ. What do you observe?
d. Complete the table to verify that the identity you wrote in part (c) is valid for angles (of your choice) in each of the four quadrants.
EXPLORATION 2
Writing Other Trigonometric Identities
Work with a partner. The trigonometric identity you derived in Exploration 1 is called a Pythagorean identity. There are two other Pythagorean identities. To derive them, recall the four relationships:

a. Divide each side of the Pythagorean identity you derived in Exploration 1 by cos2θ and simplify. What do you observe?
b. Divide each side of the Pythagorean identity you derived in Exploration 1 by sin2θ and simplify. What do you observe?
Communicate Your Answer
Question 3.
How can you verify a trigonometric identity?
Answer:
Question 4.
Is sin θ = cos θ a trigonometric identity? Explain your reasoning.
Answer:
Question 5.
Give some examples of trigonometric identities that are different than those in Explorations 1 and 2.
Answer:
Monitoring Progress
Question 1.
Given that cos θ = \(\frac{1}{6}\) and 0 < θ < \(\frac{\pi}{2}\), find the values of the other five trigonometric functions of θ.
Answer:
sin θ = \(\frac { √35 }{ 6 } \)
tan θ = √35
cot θ = \(\frac { 1 }{ √35 } \)
sec θ = 6
csc θ = \(\frac { 6 }{ √35 } \)
Explanation:
cos θ = \(\frac{1}{6}\)
adjacent side = 1
hypotenuse = 6
opposite side = √6² – 1²
= √35
sin θ = \(\frac { opposite side }{ hypotenuse } \) = \(\frac { √35 }{ 6 } \)
tan θ = \(\frac { opposite side }{ adjacent side } \) = \(\frac { √35 }{ 1 } \)
cot θ = \(\frac { adjacent side }{ opposite side } \) = \(\frac { 1 }{ √35 } \)
sec θ = \(\frac { hypotenuse }{ adjacent side } \) = \(\frac { 6 }{ 1 } \)
csc θ = \(\frac { hypotenuse }{ opposite side } \) = \(\frac { 6 }{ √35 } \)
Simplify the expression.
Question 2.
sin x cot x sec x
Answer:
sin x cot x sec x = 1
Explanation:
cot x = \(\frac { cos x }{ sin x } \)
sec x = \(\frac { 1 }{ cos x } \)
sin x cot x sec x = sin x . \(\frac { cos x }{ sin x } \) . \(\frac { 1 }{ cos x } \)
= 1
Question 3.
cos θ − cos θ sin2θ
Answer:
cos θ − cos θ sin2θ = cos³θ
Explanation:
cos θ − cos θ sin²θ = cos θ(1 – sin²θ)
= cos θ . cos²θ
= cos³θ
Question 4.
\(\frac{\tan x \csc x}{\sec x}\)
Answer:
\(\frac{\tan x \csc x}{\sec x}\) = 1
Explanation:
tan x = \(\frac { sin x }{ cos x } \)
cosec x = \(\frac { 1 }{ sin x } \)
sec x = \(\frac { 1 }{ cos x } \)
\(\frac{\tan x \csc x}{\sec x}\) = \(\frac { [latex]\frac { sin x }{ cos x } \) . \(\frac { 1 }{ sin x } \) }{ \(\frac { 1 }{ cos x } \) } [/latex]
= 1
Verify the identity.
Question 5.
cot(−θ) =−cot θ
Answer:
cot θ = \(\frac { cos θ }{ sin θ } \)
sin(−θ) =−sin θ
cos(−θ) = cos θ
cot(−θ) = \(\frac { sin(−θ) }{ cos(−θ) } \)
= \(\frac { -sin θ }{ cos θ } \) = – cot θ
Question 6.
csc2x(1 − sin2x) = cot2x
Answer:
cot²x = \(\frac { cos²x }{ sin²x } \)
csc²x = \(\frac { 1 }{ sin²x } \)
1 − sin²x = cos²x
csc²x(1 − sin²x) = \(\frac { 1 }{ sin²x } \) . cos²x
= \(\frac { cos²x }{ sin²x } \)
= cot²x
Question 7.
cos x csc x tan x = 1
Answer:
csc x = \(\frac { 1 }{ sin x } \)
tan x = \(\frac { sin x }{ cos x } \)
cos x csc x tan x = cos x . \(\frac { 1 }{ sin x } \) .\(\frac { sin x }{ cos x } \)
= 1
Question 8.
(tan2x + 1)(cos2x− 1) = −tan2x
Answer:
tan²x = \(\frac { sin²x }{ cos²x } \)
cos²x + sin²x = 1
1 – cos²x = sin²x
(tan²x + 1)(cos²x− 1) = (\(\frac { sin²x }{ cos²x } \) + 1) . (cos²x− 1)
= \(\frac { sin²x + cos²x }{ cos²x } \) . (-(1 – cos²x))
= \(\frac { 1 }{ cos²x } \) . (-sin²x)
= \(\frac { -sin²x }{ cos²x } \)
= −tan²x
Using Trigonometric Identities 9.7 Exercises
Vocabulary and Core Concept Check
Question 1.
WRITING
Describe the difference between a trigonometric identity and a trigonometric equation.
Answer:
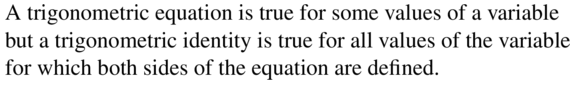
Question 2.
WRITING
Explain how to use trigonometric identities to determine whether sec(−θ) = sec θ or sec(−θ) = −sec θ.
Answer:
sec(−θ) = sec θ
Explanation:
sec θ = \(\frac { 1 }{ cos θ } \)
cos(-θ) = cosθ
sec(-θ) = \(\frac { 1 }{ cos(-θ) } \) = \(\frac { 1 }{ cos θ } \) = sec θ
Monitoring Progress and Modeling with Mathematics
In Exercises 3–10, find the values of the other five trigonometric functions of θ.
Question 3.
sinθ = \(\frac{1}{3}\), 0 < θ < \(\frac{\pi}{2}\)
Answer:

Question 4.
sin θ = −\(\frac{7}{10}\), π < θ < \(\frac{3 \pi}{2}\)
Answer:
cos θ = \(\frac { √51 }{ 10 } \)
tan θ = \(\frac { 7√51 }{ 51 } \)
cot θ = \(\frac{√51}{7}\)
sec θ = –\(\frac { 10√51 }{ 51 } \)
csc θ = −\(\frac{10}{7}\)
Explanation:
sin θ = −\(\frac{7}{10}\)
cos² θ = 1 – sin²θ
= 1 – (−\(\frac{7}{10}\))²
= \(\frac { 51 }{ 100 } \)
cos θ = \(\frac { √51 }{ 10 } \)
tan θ = \(\frac { sin θ }{ cos θ } \) = \(\frac { -7/10 }{ √51/10 } \) = \(\frac { 7√51 }{ 51 } \)
cot θ = \(\frac { cos θ }{ sin θ } \) = \(\frac { √51/10 }{ −7/10 } \) = \(\frac{√51}{7}\)
sec θ = \(\frac { 1 }{ cos θ } \) = –\(\frac { 10√51 }{ 51 } \)
csc θ = \(\frac { 1 }{ sin θ } \) = −\(\frac{10}{7}\)
Question 5.
tanθ = −\(\frac{3}{7}\), \(\frac{\pi}{2}\) < θ < π
Answer:

Question 6.
cot θ = −\(\frac{2}{5}\), \(\frac{\pi}{2}\) < θ < π
Answer:
sin θ = \(\frac{5√29}{29}\)
cos θ = \(\frac{-2√29}{29}\)
tan θ = \(\frac { 5 }{ 2 } \)
sec θ = –\(\frac { √29 }{ 2 } \)
csc θ = \(\frac{√29}{5}\)
Explanation:
cot θ = −\(\frac{2}{5}\)
\(\frac { cos θ }{ sin θ } \) = −\(\frac{2}{5}\)
cos θ = −\(\frac{2}{5}\)sin θ
cos² θ + sin²θ = 1
\(\frac{4}{25}\)sin² θ + sin² θ = 1
sin² θ = \(\frac { 25 }{ 29 } \)
sin θ = \(\frac{5√29}{29}\)
cos θ = −\(\frac{2}{5}\) . \(\frac{5√29}{29}\)
= \(\frac{-2√29}{29}\)
tan θ = \(\frac { sin θ }{ cos θ } \) = \(\frac { 5√29/29 }{ -2√29/29 } \) = \(\frac { 5 }{ 2 } \)
sec θ = \(\frac { 1 }{ cos θ } \) = –\(\frac { √29 }{ 2 } \)
csc θ = \(\frac { 1 }{ sin θ } \) = \(\frac{√29}{5}\)
Question 7.
cos θ = −\(\frac{5}{6}\), π < θ < \(\frac{3 \pi}{2}\)
Answer:

Question 8.
sec θ = \(\frac{9}{4}\), \(\frac{3 \pi}{2}\) < θ < 2π
Answer:
sin θ = –\(\frac{√65}{9}\)
cos θ = \(\frac{4}{9}\)
tan θ = \(\frac { -√65 }{ 4 } \)
cot θ = –\(\frac { 4√65 }{ 65 } \)
csc θ = \(\frac{-9√65}{65}\)
Explanation:
sec θ = \(\frac{9}{4}\)
\(\frac { 1 }{ cos θ } \) = \(\frac{9}{4}\)
cos θ = \(\frac{4}{9}\)
cos² θ + sin²θ = 1
sin²θ = 1 – cos² θ
= 1 – (\(\frac{16}{81}\))
= \(\frac{65}{81}\)
sin θ = –\(\frac{√65}{9}\)
tan θ = \(\frac { sin θ }{ cos θ } \) = \(\frac { -√65/9 }{ 4/9 } \) = \(\frac { -√65 }{ 4 } \)
cot θ = \(\frac { cos θ }{ sin θ } \) = \(\frac { 4/9 }{ -√65/9 } \) = \(\frac { -4√65 }{ 65 } \)
csc θ = \(\frac { 1 }{ sin θ } \) = \(\frac{-9√65}{65}\)
Question 9.
cot θ = −3, \(\frac{3 \pi}{2}\) < θ < 2π
Answer:

Question 10.
csc θ = −\(\frac{5}{3}\), π < θ < \(\frac{3 \pi}{2}\)
Answer:
sin θ = −\(\frac{3}{5}\)
cos θ = –\(\frac{4}{5}\)
tan θ = \(\frac { 3 }{ 4 } \)
cot θ = –\(\frac { 4}{ 3 } \)
sec θ = \(\frac{-5}{4}\)
Explanation:
csc θ = −\(\frac{5}{3}\)
\(\frac { 1 }{ sin θ } \) = −\(\frac{5}{3}\)
sin θ = −\(\frac{3}{5}\)
cos² θ + sin²θ = 1
cos²θ = 1 – sin² θ
= 1 – (\(\frac{9}{25}\))
= \(\frac{16}{25}\)
cos θ = –\(\frac{4}{5}\)
tan θ = \(\frac { sin θ }{ cos θ } \) = \(\frac { −3/5 }{ -4/5 } \) = \(\frac { 3 }{ 4 } \)
cot θ = \(\frac { cos θ }{ sin θ } \) = \(\frac { -4/5 }{ −3/5 } \) = \(\frac { 4 }{ 3 } \)
sec θ = \(\frac { 1 }{ cos θ } \) = \(\frac{-5}{4}\)
In Exercises 11–20, simplify the expression.
Question 11.
sin x cot x
Answer:

Question 12.
cos θ (1 + tan2θ)
Answer:
cos θ (1 + tan2θ) = sec θ
Explanation:
cos θ (1 + tan²θ) = cos θ (1 + \(\frac { sin² θ }{ cos² θ } \))
= cos θ(\(\frac { cos² θ + sin² θ }{ cos² θ } \)
= cos θ(\(\frac { 1 }{ cos² θ } \))
= \(\frac { 1 }{ cos θ } \)
= sec θ
Question 13.
\(\frac{\sin (-\theta)}{\cos (-\theta)}\)
Answer:

Question 14.
\(\frac{\cos ^{2} x}{\cot ^{2} x}\)
Answer:
\(\frac{\cos ^{2} x}{\cot ^{2} x}\) = sin² x
Explanation:
cot θ = \(\frac { cos θ }{ sin θ } \)
\(\frac{\cos ^{2} x}{\cot ^{2} x}\) = \(\frac { cos² x }{ cos² x/sin² x } \)
= \(\frac { sin² x . cos² x}{ cos² x } \)
= sin² x
Question 15.
\(\frac{\cos \left(\frac{\pi}{2}-x\right)}{\csc x} \)
Answer:
Question 16.
sin(\(\frac{\pi}{2}\) – θ) sec θ
Answer:
sin(\(\frac{\pi}{2}\) – θ) sec θ = 1
Explanation:
sin(\(\frac{\pi}{2}\) – θ) = cos θ
sec θ = \(\frac { 1 }{ cos θ } \)
sin(\(\frac{\pi}{2}\) – θ) sec θ = cos θ . \(\frac { 1 }{ cos θ } \)
= 1
Question 17.
\(\frac{\csc ^{2} x-\cot ^{2} x}{\sin (-x) \cot x}\)
Answer:

Question 18.
\(\frac{\cos ^{2} x \tan ^{2}(-x)-1}{\cos ^{2} x}\)
Answer:
\(\frac{\cos ^{2} x \tan ^{2}(-x)-1}{\cos ^{2} x}\) = -1
Explanation:
tan x = \(\frac { sin x }{ cos x } \)
tan(-x) = – tan x
sin²x – 1 = – cos² x
\(\frac{\cos ^{2} x \tan ^{2}(-x)-1}{\cos ^{2} x}\) = \(\frac {cos² x . sin² x / cos² x – 1 }{ cos² x } \)
= \(\frac { sin² x – 1 }{ cos² x } \)
= \(\frac { -cos² x }{ cos² x } \)
= -1
Question 19.
\(\frac{\cos \left(\frac{\pi}{2}-\theta\right)}{\csc \theta}\) + cos2 θ
Answer:
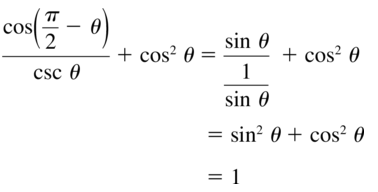
Question 20.
\(\frac{\sec x \sin x+\cos \left(\frac{\pi}{2}-x\right)}{1+\sec x}\)
Answer:
\(\frac{\sec x \sin x+\cos \left(\frac{\pi}{2}-x\right)}{1+\sec x}\) = sin x
Explanation:
cos(\(\frac { π }{ 2 } \) – x) = sin x
sec x = \(\frac { 1 }{ cos x } \)
\(\frac{\sec x \sin x+\cos \left(\frac{\pi}{2}-x\right)}{1+\sec x}\) = \(\frac { 1/cosx . sin x + sin x }{ 1 + 1/cosx } \)
= \(\frac { sinx/cosx + sin x }{ (cosx + 1)/ cosx } \)
= \(\frac { (sin x + sinx cosx) / cos x }{ (cos x + 1)/ cos x } \)
= \(\frac { sin x(1 + cos x) }{ cos x + 1 } \)
= sin x
ERROR ANALYSIS In Exercises 21 and 22, describe and correct the error in simplifying the expression.
Question 21.
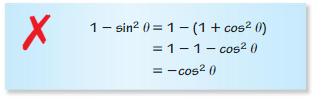
Answer:
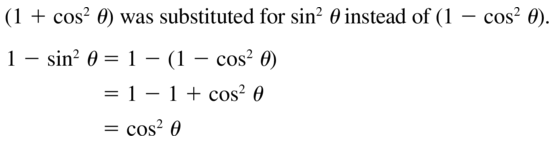
Question 22.
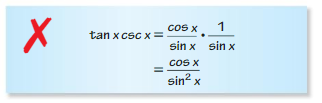
Answer:
tan x csc x = \(\frac { sin x }{ cos x } \) . \(\frac { 1 }{ sin x } \)
= \(\frac { 1 }{ cos x } \)
= sec x
In Exercises 23–30, verify the identity.
Question 23.
sin x csc x = 1
Answer:

Question 24.
tan θ csc θ cos θ = 1
Answer:
tan θ csc θ cos θ = \(\frac { sin θ }{ cos θ } \) . \(\frac { 1 }{ sin θ } \) cos θ
= 1
Question 25.
cos (\(\frac{3 \pi}{2}\) − x)cot x = cos x
Answer:
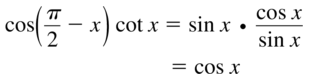
Question 26.
sin (\(\frac{ \pi}{2}\) − x)tan x = sin x
Answer:
sin (\(\frac{ \pi}{2}\) − x) = cos x
tan x = \(\frac { sin x }{ cos x } \)
sin (\(\frac{ \pi}{2}\) − x)tan x = cos x . \(\frac { sin x }{ cos x } \)
= sin x
Question 27.
\(\frac{\cos \left(\frac{\pi}{2}-\theta\right)+1}{1-\sin (-\theta)}\) = 1
Answer:
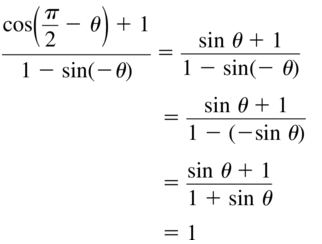
Question 28.
\(\frac{\sin ^{2}(-x)}{\tan ^{2} x}\) = cos2 x
Answer:
sin(-x) = -sin x
tan x = \(\frac { sin x }{ cos x } \)
\(\frac{\sin ^{2}(-x)}{\tan ^{2} x}\) = \(\frac { (-sin x)² }{ ( sin x /cos x )² } \)
= \(\frac { sin² x }{ sin² x /cos² x } \)
= \(\frac { sin² x cos² x}{ sin² x } \)
= cos² x
Question 29.
\(\frac{1+\cos x}{\sin x}+\frac{\sin x}{1+\cos x}\) = 2 csc x
Answer:
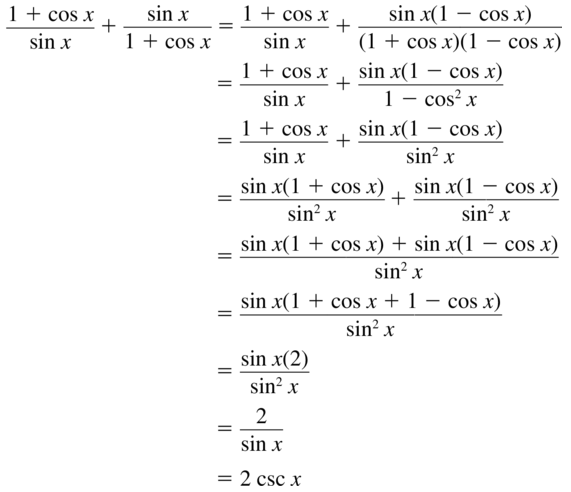
Question 30.
\(\frac{\sin x}{1-\cos (-x)}\) = csc x + cot x
Answer:
cos(-x) = cosx
\(\frac{\sin x}{1-\cos (-x)}\) = \(\frac { sin x }{ 1 – cos x } \) . \(\frac { 1 + cos x }{ 1 + cos x } \)
= \(\frac { sin x(1 + cos x) }{ (1 – cosx)(1 + cos x) } \)
= \(\frac { sin x(1 + cos x) }{ 1 – cos² x} \)
= \(\frac { sin x(1 + cos x) }{ sin² x} \)
= \(\frac { 1 + cos x }{ sin x } \)
= \(\frac { 1 }{ sin x } \) + \(\frac { cos x }{ sin x } \)
= cscx + cotx
Question 31.
USING STRUCTURE
A function f is odd when f(−x) = −f(x). A function f is even when (−x) = f (x). Which of the six trigonometric functions are odd? Which are even? Justify your answers using identities and graphs.
Answer:
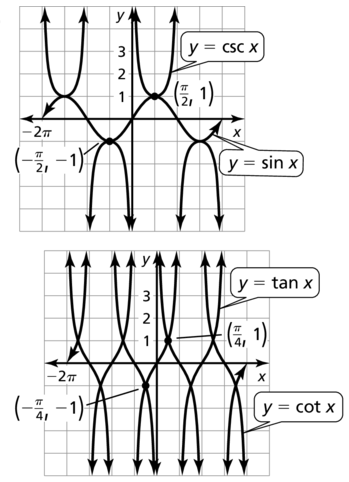
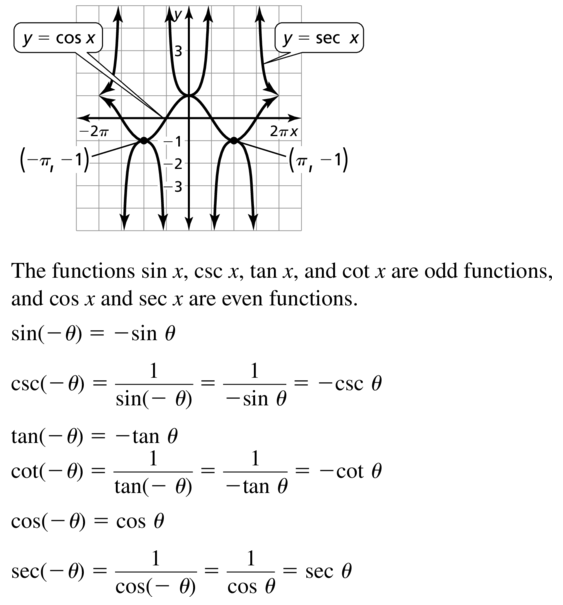
Question 32.
ANALYZING RELATIONSHIPS
As the value of cos θ increases, what happens to the value of sec θ? Explain your reasoning.
Answer:
Since the functions cosine and secant are reciprocal, the increasing of the cosine implies decreasing the secant.
Question 33.
MAKING AN ARGUMENT
Your friend simplifies an expression and obtains sec x tan x− sin x. You simplify the same expression and obtain sin x tan2x. Are your answers equivalent? Justify your answer.
Answer:

Question 34.
HOW DO YOU SEE IT?
The figure shows the unit circle and the angle θ.
a. Is sin θ positive or negative? cos θ? tan θ?
b. In what quadrant does the terminal side of −θ lie?
c. Is sin(−θ) positive or negative? cos(−θ)? tan(−θ)?

Answer:
a. sin θ > 0, cos θ < 0, tan θ < 0
b. The angle θ iis from the third quadrant
c. sin θ < 0, cos θ < 0, tan θ > 0
Explanation:
a. The angle is in the second quadrant. The value of sine in Q2 is +ve and cosine is -ve. So, tan θ is -ve
b. The angle -θ represents the angle θ measured clockwise. So, the angle -θ will be in Q3.
c. cos(-θ) = cos θ < 0
sin(-θ) = -sinθ < 0
tan(-θ) = -tanθ > 0
Question 35.
MODELING WITH MATHEMATICS
A vertical gnomon(the part of a sundial that projects a shadow) has height h. The length s of the shadow cast by the gnomon when the angle of the Sun above the horizon is θ can be modeled by the equation below. Show that the equation below is equivalent to s = h cot θ.
Answer:

Question 36.
THOUGHT PROVOKING
Explain how you can use a trigonometric identity to find all the values of x for which sin x = cos x.
Answer:
The equation has a solution if the equation 90° – x = x has a solution
Explanation:
Lets consider cos x = sin x
sin (90 – x) = cos x
sin (90 – x) = sin x
so, 90 – x = x
90 = 2x
x = 45°
Question 37.
DRAWING CONCLUSIONS
Static friction is the amount of force necessary to keep a stationary object on a flat surface from moving. Suppose a book weighing W pounds is lying on a ramp inclined at an angle θ. The coefficient of static friction u for the book can be found using the equation uW cos θ = W sin θ.
a. Solve the equation for u and simplify the result.
b. Use the equation from part (a) to determine what happens to the value of u as the angle θ increases from 0° to 90°.
Answer:
Question 38.
PROBLEM SOLVING
When light traveling in a medium (such as air) strikes the surface of a second medium (such as water) at an angle θ1, the light begins to travel at a different angle θ2. This change of direction is defined by Snell’s law, n1 sin θ1 = n2 sin θ2, where n1 and n2 are the indices of refraction for the two mediums. Snell’s law can be derived from the equation.
a. Simplify the equation to derive Snell’s law.
b. What is the value of n1 when θ1 = 55°, θ2 = 35°, and n2 = 2?
c. If θ1 = θ2, then what must be true about the values of n1 and n2? Explain when this situation would occur.
Answer:
a) n1 . sin θ1 = 2 . sin θ2
b) n1 = 1.5
c) If the angles θ1 and θ2 are equal implies that n1 = n2
Explanation:
b. n1 . sin 55 = 2 . sin 35
n1 = 1.4
c. n1 . sin θ = n2 . sin θ
n1 = n2
Question 39.
WRITING
Explain how transformations of the graph of the parent function f(x) = sin x support the cofunction identity sin (\(\frac{\pi}{2}\) − θ) = cos θ.
Answer:
Question 40.
USING STRUCTURE
Verify each identity.
a. ln ∣sec θ∣= −ln ∣cos θ∣
b. ln ∣tan θ∣= ln ∣sin θ∣− ln ∣cos θ∣
Answer:
a) To prove the equality
log (\(\frac { a }{ b } \)) = log a – log b
log |sec θ| = log |\(\frac { 1 }{ cos θ } \)|
= log \(\frac { 1 }{ |cos θ| } \)
= log 1 – log|cos θ|
= 0 – log|cos θ|
= -log|cos θ|
b) To prove the equality
log|tan θ| = log|\(\frac { sin θ }{ cos θ } \)|
= log |sin θ| – log |cos θ|
Maintaining Mathematical Proficiency
Find the value of x for the right triangle.
Question 41.
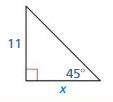
Answer:

Question 42.
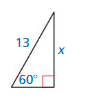
Answer:
x = 13.5
Explanation:
cos 60 = \(\frac { x }{ 13 } \)
0.5 = \(\frac { x }{ 13 } \)
x = 13.5
Question 43.
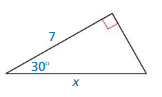
Answer:

Lesson 9.8 Using Sum and Difference Formulas
Essential Question How can you evaluate trigonometric functions of the sum or difference of two angles?
EXPLORATION 1
Deriving a Difference Formula
Work with a partner.
a. Explain why the two triangles shown are congruent.
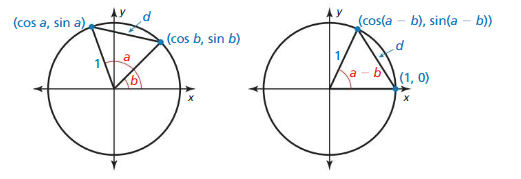
b. Use the Distance Formula to write an expression for d in the first unit circle.
c. Use the Distance Formula to write an expression for d in the second unit circle.
d. Write an equation that relates the expressions in parts (b) and (c). Then simplify this equation to obtain a formula for cos(a − b).
EXPLORATION 2
Deriving a Sum Formula

Work with a partner. Use the difference formula you derived in Exploration 1 to write a formula for cos(a+b) in terms of sine and cosine of a and b. Hint: Use the fact that cos(a+b) = cos[a − (−b)].
EXPLORATION 3
Deriving Difference and Sum Formulas
Work with a partner. Use the formulas you derived in Explorations 1 and 2 to write formulas for sin(a − b) and sin(a + b) in terms of sine and cosine of a and b. Hint: Use the cofunction identities sin (\(\frac{\pi}{2}\) − a)= cos a and cos (\(\frac{\pi}{2}\) − a)= sin a and the fact that
cos [(\(\frac{\pi}{2}\) − a) + b ]= sin(a − b) and sin(a+b) = sin[a − (−b)].
Communicate Your Answer
Question 4.
How can you evaluate trigonometric functions of the sum or difference of two angles?
Answer:
Question 5.
a. Find the exact values of sin 75° and cos 75° using sum formulas. Explain your reasoning.
b. Find the exact values of sin 75° and cos 75° using difference formulas. Compare your answers to those in part (a).
Answer:
Monitoring Progress
Find the exact value of the expression.
Question 1.
sin 105°
Answer:
sin 105° = \(\frac { √6 + √4 }{ 4 } \)
Explanation:
sin 105° = sin (45 + 60)
= sin 45° cos 60° + sin 60° cos 45°
= \(\frac { √2 }{ 2 } \) . \(\frac { √3 }{ 2 } \) + \(\frac { √3 }{ 2 } \) . \(\frac { 1 }{ 2 } \)
= \(\frac { √6 }{ 4 } \) + \(\frac { √2 }{ 4 } \)
= \(\frac { √6 + √4 }{ 4 } \)
Question 2.
cos 15°
Answer:
cos 15° = \(\frac { √6 + √2 }{ 4 } \)
Explanation:
cos 15° = cos(60° – 45°)
= cos 60° cos 45° + sin 60° sin 45°
= \(\frac { 1 }{ 2 } \) . \(\frac { √2 }{ 2 } \) + \(\frac { √3 }{ 2 } \) . \(\frac { √2 }{ 2 } \)
= \(\frac { √2 }{ 4 } \) + \(\frac { √6 }{ 4 } \)
= \(\frac { √6 + √2 }{ 4 } \)
Question 3.
tan \(\frac{5 \pi}{2}\)
Answer:
tan \(\frac{5 \pi}{2}\) = 2 + √3
Explanation:
tan \(\frac{5 \pi}{2}\) = tan(\(\frac { π }{ 4 } \) + \(\frac { π }{ 6 } \))
= \(\frac { tanπ/4 + tanπ/6 }{ 1 – tanπ/4 . tanπ/6} \)
= \(\frac { 1 + √3/3 }{ 1 – 1 . √3/3 } \)
= \(\frac { 3 + √3 }{ 3 – √3 } \)
= \(\frac { 3 + √3 }{ 3 – √3 } . \frac { 3 + √3 }{ 3 + √3 } \)
= \(\frac { (3 + √3)² }{ 9 – 3 } \)
= \(\frac { 9 + 6√3 + 3 }{ 6 } \)
= \(\frac { 6(2 + √3) }{ 6 } \)
= 2 + √3
Question 4.
cos \(\frac{\pi}{12}\)
Answer:
cos \(\frac{\pi}{12}\) = \(\frac { √6 + √2 }{ 4 } \)
Explanation:
cos \(\frac{\pi}{12}\) = cos(\(\frac { π }{ 3 } \) – \(\frac { π }{ 4 } \))
= cos\(\frac { π }{ 3 } \) cos \(\frac { π }{ 4 } \) + sin\(\frac { π }{ 3 } \) sin \(\frac { π }{ 4 } \)
= \(\frac { 1 }{ 2 } \) . \(\frac { √2 }{ 2 } \) + \(\frac { √3 }{ 2 } \) . \(\frac { √2 }{ 2 } \)
= \(\frac { √2 }{ 4 } \) + \(\frac { √6 }{ 4 } \)
= \(\frac { √6 + √2 }{ 4 } \)
Question 5.
Find sin(a−b) given that sin a = \(\frac{8}{17}\) with 0 < a < \(\frac{\pi}{2}\) and cos b = −\(\frac{24}{25}\) with π < b < \(\frac{3 \pi}{2}\) .
Answer:
sin(a – b) = –\(\frac { 87 }{ 425 } \)
Explanation:
sin a = \(\frac{8}{17}\)
cos b = −\(\frac{24}{25}\)
cos² a = 1 – sin² a
= 1 – (\(\frac{8}{17}\))²
= 1 – \(\frac{64}{289}\)
= \(\frac{289 – 64}{289}\)
= \(\frac{225}{289}\)
cos a = ±\(\frac{15}{17}\)
Since the angle is in the first quadrant, the value of cos is +ve
So, cos a = \(\frac{15}{17}\)
sin² b = 1 – cos² b
= 1 – (−\(\frac{24}{25}\))²
= 1 – \(\frac{576}{625}\)
= \(\frac{625 – 576}{625}\)
= \(\frac{49}{625}\)
sin b = ±\(\frac{7}{25}\)
Since the angle b is in Q3, the value of sin is -ve
so, sin b = –\(\frac{7}{25}\)
sin(a – b) = sin a cos b – cos a sin b
= \(\frac{8}{17}\) . \(\frac{-24}{25}\) – \(\frac{15}{17}\) . \(\frac{-7}{25}\)
= \(\frac{-192}{425}\) + \(\frac{105}{425}\)
= \(\frac{-192 + 105}{425}\)
= \(\frac{-87}{425}\)
Simplify the expression.
Question 6.
sin(x + π)
Answer:
sin(x + π) = sinx cosπ + cosx sinπ
= sinx(-) + cosx()
= -sinx
Question 7.
cos(x − 2π)
Answer:
cos(x − 2π) = cosx cos2π + sinx sin2π
= cosx (1) + sinx (0)
= cosx
Question 8.
tan(x − π)
Answer:
tan(x − π) = \(\frac { tan x – tan π }{ 1 + tan x tan π } \)
= \(\frac { tan x – 0 }{ 1 + tan x . 0 } \)
= tan x
Question 9.
Solve sin (\(\frac{\pi}{4}\) − x)− sin (x + \(\frac{\pi}{4}\))= 1 for 0 ≤ x < 2π.
Answer:
The solutions of the equations are x = \(\frac { π }{ 4 } \) & x = \(\frac { 7π }{ 4 } \)
Explanation:
sin (x + \(\frac{\pi}{4}\)) = sin x cos\(\frac { π }{ 4 } \) + cos x sin\(\frac { π }{ 4 } \)
= sinx . \(\frac { √2 }{ 2 } \) + cosx . \(\frac { √2 }{ 2 } \)
= \(\frac { √2 }{ 2 } \)cos x + \(\frac { √2 }{ 2 } \)sin x
sin (x – \(\frac{\pi}{4}\)) = sin x cos\(\frac { π }{ 4 } \) – cos x sin\(\frac { π }{ 4 } \)
= sinx . \(\frac { √2 }{ 2 } \) – cosx . \(\frac { √2 }{ 2 } \)
= \(\frac { √2 }{ 2 } \)(sin x – cos x)
sin (\(\frac{\pi}{4}\) − x)− sin (x + \(\frac{\pi}{4}\))= 1
– \(\frac { √2 }{ 2 } \)cos x + \(\frac { √2 }{ 2 } \)sin x – \(\frac { √2 }{ 2 } \)cos x – \(\frac { √2 }{ 2 } \)sin x = 1
√2 sinx = 1
sin x = \(\frac { 1 }{ √2 } \)
= \(\frac { √2 }{ 2 } \)
x = \(\frac { π }{ 4 } \)
the sine is also positive in 4th qudrant.
So, x = 2π – \(\frac { π }{ 4 } \) = \(\frac { 7π }{ 4 } \)
Using Sum and Difference Formulas 9.8 Exercises
Vocabulary and Core Concept Check
Question 1.
COMPLETE THE SENTENCE
Write the expression cos 130° cos 40°− sin 130° sin 40° as the cosine of an angle.
Answer:
![]()
Question 2.
WRITING
Explain how to evaluate tan 75° using either the sum or difference formula for tangent.
Answer:
tan 75° = 3.728
Explanation:
tan 75° = tan(45° + 30°)
= \(\frac { tan 45° + tan 30° }{ 1 – tan 45° tan 30° } \)
= \(\frac { 1 + 1/√3 }{ 1 – 1 . 1/√3 } \)
= \(\frac { 1.577 }{ 0.423 } \)
= 3.728
Monitoring Progress and Modeling with Mathematics
In Exercises 3–10, find the exact value of the expression.
Question 3.
tan(−15°)
Answer:
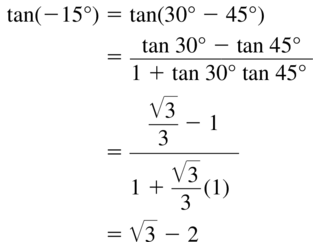
Question 4.
tan 195°
Answer:
tan 195° = 2 – √3
Explanation:
tan 195° = tan(225° – 30°)
= \(\frac { tan 225° – tan 30° }{ 1 + tan 225° tan 30° } \)
= \(\frac { 1 – 1/√3 }{ 1 + 1 . 1/√3 } \)
= \(\frac { 3 – √3 }{ 3 + √3 } . \frac { 3 – √3 }{ 3 – √3 } \)
= \(\frac { 9 – 6√3 + 3 }{ 9 – 3 } \)
= \(\frac { 12 – 6√3 }{ 6 } \)
= 2 – √3
Question 5.
sin \(\frac{23 \pi}{12}\)
Answer:
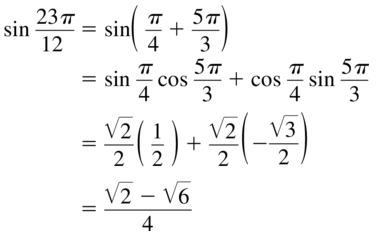
Question 6.
sin(−165°)
Answer:
sin(−165°) = \(\frac { √2 – √6 }{ 4 } \)
Explanation:
sin(−165°) = – sin 165°
sin 165° = sin(120° + 45°)
= sin 120° cos 45° + cos 120° sin 45°
= \(\frac { √3 }{ 2 } \) . \(\frac { √2 }{ 2 } \) + (\(\frac { -1 }{ 2 } \)). \(\frac { √2 }{ 2 } \)
= \(\frac { √6 – √2 }{ 4 } \)
sin(−165°) = – sin 165° = \(\frac { √2 – √6 }{ 4 } \)
Question 7.
cos 105°
Answer:
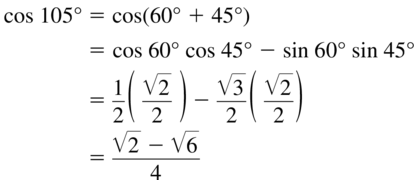
Question 8.
cos \(\frac{11 \pi}{12}\)
Answer:
cos \(\frac{11 \pi}{12}\) = -(\(\frac { √2 + √6 }{ 4 } \)
Explanation:
cos \(\frac{\pi}{12}\) = cos(\(\frac { π }{ 3 } \) – \(\frac { π }{ 4 } \))
= cos\(\frac { π }{ 3 } \)cos\(\frac { π }{ 4 } \) + sin\(\frac { π }{ 3 } \)sin\(\frac { π }{ 4 } \)
= \(\frac { 1 }{ 2 } \) . \(\frac { √2 }{ 2 } \) + \(\frac { √3 }{ 2 } \) . \(\frac { √2 }{ 2 } \)
= \(\frac { √2 + √6 }{ 4 } \)
cos \(\frac{11 \pi}{12}\) = cos (π – \(\frac{\pi}{12}\)) = – cos\(\frac{\pi}{12}\) = -(\(\frac { √2 + √6 }{ 4 } \)
Question 9.
tan \(\frac{17 \pi}{12}\)
Answer:
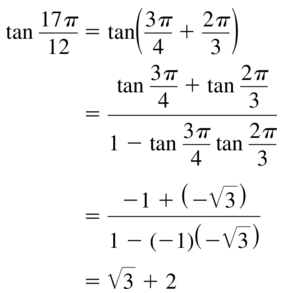
Question 10.
sin (−\(\frac{7 \pi}{12}\))
Answer:
sin (−\(\frac{7 \pi}{12}\)) = \(\frac { -√2 – √6 }{ 4 } \)
Explanation:
sin (−\(\frac{7 \pi}{12}\)) = – sin\(\frac{7 \pi}{12}\)
sin\(\frac{7 \pi}{12}\) = sin(\(\frac { π }{ 2 } \) + \(\frac { π }{ 12 } \)) = cos \(\frac { π }{ 12 } \)
cos \(\frac { π }{ 12 } \) = cos(\(\frac { π }{ 3 } \) – \(\frac { π }{ 4 } \))
= cos\(\frac { π }{ 3 } \)cos\(\frac { π }{ 4 } \) + sin\(\frac { π }{ 3 } \)sin\(\frac { π }{ 4 } \)
= \(\frac { 1 }{ 2 } \) . \(\frac { √2 }{ 2 } \) + \(\frac { √3 }{ 2 } \) . \(\frac { √2 }{ 2 } \)
= \(\frac { √2 + √6 }{ 4 } \)
sin (−\(\frac{7 \pi}{12}\)) = -sin\(\frac{7 \pi}{12}\) = \(\frac { -√2 – √6 }{ 4 } \)
In Exercises 11–16, evaluate the expression given that cos a = \(\frac{4}{5}\) with 0 < a < \(\frac{\pi}{2}\) and sin b = –\(\frac{15}{17}\) with \(\frac{3 \pi}{2}\) < b < 2π.
Question 11.
sin(a + b)
Answer:

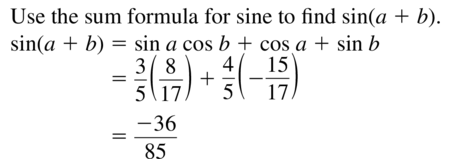
Question 12.
sin(a − b)
Answer:
sin(a − b) = \(\frac { 84 }{ 85 } \)
Explanation:
sin a = \(\frac { 3 }{ 5 } \)
cos a = \(\frac { 4 }{ 5 } \)
sin b = –\(\frac { 15 }{ 17 } \)
cos b = \(\frac { 8 }{ 17 } \)
sin(a – b) = sin a cos b – cos a sin b
= \(\frac { 3 }{ 5 } \) . \(\frac { 8 }{ 17 } \) – \(\frac { 4 }{ 5 } \) . (-\(\frac { 15 }{ 17 } \))
= \(\frac { 24 }{ 85 } \) + \(\frac { 60 }{ 85 } \)
= \(\frac { 84 }{ 85 } \)
Question 13.
cos(a − b)
Answer:

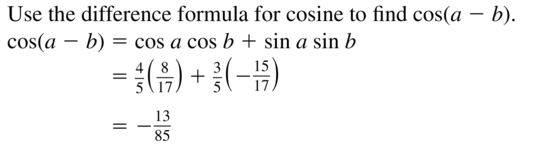
Question 14.
cos(a + b)
Answer:
cos(a + b) = \(\frac { 77 }{ 85 } \)
Explanation:
sin a = \(\frac { 3 }{ 5 } \)
cos a = \(\frac { 4 }{ 5 } \)
sin b = –\(\frac { 15 }{ 17 } \)
cos b = \(\frac { 8 }{ 17 } \)
cos(a – b) = cos a cos b – sin a sin b
= \(\frac { 4 }{ 5 } \) . \(\frac { 8 }{ 17 } \) – \(\frac { 3 }{ 5 } \) . (-\(\frac { 15 }{ 17 } \))
= \(\frac { 35 }{ 85 } \) + \(\frac { 45 }{ 85 } \)
= \(\frac { 77 }{ 85 } \)
Question 15.
tan(a + b)
Answer:


Question 16.
tan(a − b)
Answer:
tan(a − b) = \(\frac { -84 }{ 13 } \)
Explanation:
sin a = \(\frac { 3 }{ 5 } \)
cos a = \(\frac { 4 }{ 5 } \)
sin b = –\(\frac { 15 }{ 17 } \)
cos b = \(\frac { 8 }{ 17 } \)
tan a = \(\frac { 3 }{ 4 } \)
tan b = \(\frac { -15 }{ 8 } \)
tan (a – b) = \(\frac { tan a – tan b }{ 1 + tan a tan b } \)
= \(\frac { 3/4] + 15/8 }{ 1 – 3/4 . 15/8 } \)
= \(\frac { -84 }{ 13 } \)
In Exercises 17–22, simplify the expression.
Question 17.
tan(x + π)
Answer:
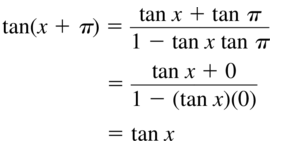
Question 18.
cos (x − \(\frac{\pi}{2}\))
Answer:
cos (x − \(\frac{\pi}{2}\)) = sin x
Explanation:
cos (x − \(\frac{\pi}{2}\)) = cosx . cos (\(\frac{\pi}{2}\)) + sin x . sin \(\frac{\pi}{2}\)
= cos x . 0 + sin x . 1
= sin x
Question 19.
cos(x + 2π)
Answer:

Question 20.
tan(x − 2π)
Answer:
tan(x − 2π) = tan x
Explanation:
tan(x − 2π) = \(\frac { tan x + tan 2π }{ 1 – tan x tan 2π } \)
= \(\frac { tan x + 0 }{ 1 – tan x . 0} \)
= tan x
Question 21.
sin (x − \(\frac{3 \pi}{2}\))
Answer:
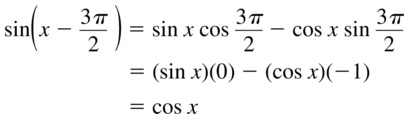
Question 22.
tan (x + \(\frac{\pi}{2}\))
Answer:
tan (x + \(\frac{\pi}{2}\)) = – cotx
Explanation:
tan (x + \(\frac{\pi}{2}\)) = \(\frac { tanx + tanπ/2 }{ 1 – tanx tanπ/2 } \)
= \(\frac { sinx/cosx+ sinπ/2/cosπ/2 }{ 1 – sinx/cosx . sinπ/2/cosπ/2 } \)
= \(\frac { sin x . 0 + 1 . cos x }{ cos x . 0 – sin x . 1 } \)
= \(\frac { -cosx }{ sinx } \)
= -cotx
ERROR ANALYSIS In Exercises 23 and 24, describe and correct the error in simplifying the expression.
Question 23.

Answer:

Question 24.
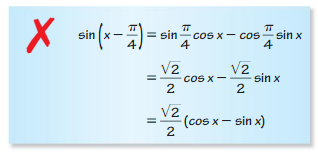
Answer:
sin (x – \(\frac { π }{ 4 } \)) = sinx cos\(\frac { π }{ 4 } \) – cosx sin\(\frac { π }{ 4 } \)
= sinx . \(\frac { √2 }{ 2 } \) – cosx . \(\frac { √2 }{ 2 } \)
= \(\frac { √2 }{ 2 } \)(sin x – cos x)
Question 25.
What are the solutions of the equation 2 sin x − 1 = 0 for 0 ≤ x < 2π?
A. \(\frac{\pi}{3}\)
B. \(\frac{\pi}{6}\)
C. \(\frac{2 \pi}{3}\)
D. \(\frac{5 \pi}{6}\)
Answer:

Question 26.
What are the solutions of the equation tan x + 1 = 0 for 0 ≤ x < 2π?
A. \(\frac{\pi}{4}\)
B. \(\frac{3 \pi}{4}\)
C. \(\frac{5 \pi}{4}\)
D. \(\frac{7 \pi}{4}\)
Answer:
B, D
Explanation:
Solve the equation on the interval 0 ≤ x ≤ 2π
tanx + 1 = 0
tanx = -1
tan\(\frac { π }{ 4 } \) = – tanx
x = π – \(\frac { π }{ 4 } \) = \(\frac { 3π }{ 4 } \)
Thus, x = \(\frac { 3π }{ 4 } \) is one solution of the equation
tan(2π – x) = – tanx
x = 2π – \(\frac { π }{ 4 } \) = \(\frac { 7π }{ 4 } \)
Hence, the second solution is x = \(\frac { 7π }{ 4 } \)
In Exercises 27–32, solve the equation for 0 ≤ x < 2π.
Question 27.
sin (x + \(\frac{\pi}{2}\)) = \(\frac{1}{2}\)
Answer:
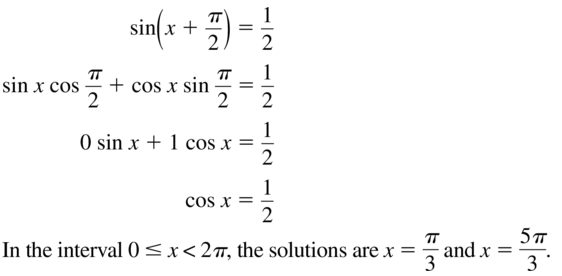
Question 28.
tan (x − \(\frac{\pi}{4}\)) = 0
Answer:
x = \(\frac { π }{ 4 } \) and x = \(\frac { 5π }{ 4 } \)
Explanation:
tan(x – \(\frac { π }{ 4 } \)) = 0
\(\frac { tanx – tanπ/4 }{ 1 + tanx tanπ/4 } \) = 0
\(\frac { tanx – 1 }{ 1 + tanx } \) = 0
tanx – 1 = 0
tanx = 1
x = \(\frac { π }{ 4 } \)
Thus, x = \(\frac { π }{ 4 } \) is one solution
tan(π + x) = tanx
x = π + \(\frac { π }{ 4 } \) = \(\frac { 5π }{ 4 } \)
Hence, x = \(\frac { 5π }{ 4 } \) is the second solution
Question 29.
cos (x +\(\frac{\pi}{6}\)) − cos (x −\(\frac{\pi}{6}\)) = 1
Answer:
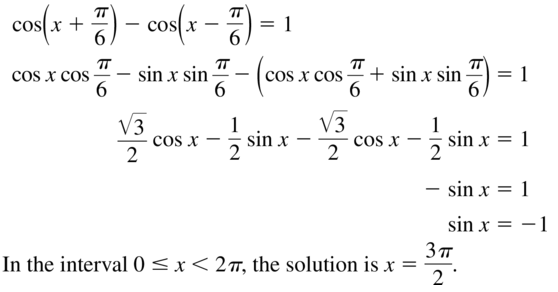
Question 30.
sin (x + \(\frac{\pi}{4}\)) + sin (x − \(\frac{\pi}{4}\)) = 0
Answer:
The solutions of the equation are x = 0, x = π
Explanation:
sin (x + \(\frac{\pi}{4}\)) + sin (x − \(\frac{\pi}{4}\)) = 0
sinx cos\(\frac { π }{ 4 } \) + cosx sin\(\frac { π }{ 4 } \) + sinx cos\(\frac { π }{ 4 } \) – cosx sin\(\frac { π }{ 4 } \) = 0
2sinx cos\(\frac { π }{ 4 } \) = 0
2 sinx . \(\frac { √2 }{ 2 } \) = 0
sin x = 0
So, x = 0, x = π
Question 31.
tan(x + π) − tan(π − x) = 0
Answer:
Question 32.
sin(x + π) + cos(x + π) = 0
Answer:
The solutions of the equation are x = \(\frac { 3π }{ 4 } \), x = \(\frac { 7π }{ 4 } \)
Explanation:
sin(x + π) + cos(x + π) = 0
sinx cosπ + cosx sinπ + cosx cosπ + sinx sinπ = 0
sinx (-1) + cosx . 0 + cosx (-1) – sinx . 0 = 0
-sinx – cosx = 0
-sinx = cosx
tanx = -1
tan\(\frac { π }{ 4 } \) = 1
tan(π – x) = -tanx
x = π – \(\frac { π }{ 4 } \) = \(\frac { 3π }{ 4 } \)
tan(2π – x) = -tanx
x = 2π – \(\frac { π }{ 4 } \) = \(\frac { 7π }{ 4 } \)
Question 33.
USING EQUATIONS
Derive the cofunction identity sin (\(\frac{\pi}{2}\) − θ)= cos θ using the difference formula for sine.
Answer:

Question 34.
MAKING AN ARGUMENT
Your friend claims it is possible to use the difference formula for tangent to derive the cofunction identity tan (\(\frac{\pi}{2}\) − θ) = cot θ. Is your friend correct? Explain your reasoning.
Answer:
My friend is not correct
Explanation:
Given that
tan(\(\frac { π }{ 2 } \) – θ) = cotθ
tan(\(\frac { π }{ 2 } \) – θ) = \(\frac{ tan π/2 – tan θ }{ 1+tan π/2tanθ } \)
So, my friend is not correct.
Question 35.
MODELING WITH MATHEMATICS
A photographer is at a height h taking aerial photographs with a 35-millimeter camera. The ratio of the image length WQ to the length NA of the actual object is given by the formula

where θ is the angle between the vertical line perpendicular to the ground and the line from the camera to point A and t is the tilt angle of the film. When t = 45°, show that the formula can be rewritten as \(\frac{W Q}{N A}=\frac{70}{h(1+\tan \theta)}\).
Answer:
Question 36.
MODELING WITH MATHEMATICS
When a wave travels through a taut string, the displacement y of each point on the string depends on the time t and the point’s position x. The equation of a standing wave can be obtained by adding the displacements of two waves traveling in opposite directions. Suppose a standing wave can be modeled by the formula
y = A cos (\(\frac{2 \pi t}{3}-\frac{2 \pi x}{5}\)) + A cos (\(\frac{2 \pi t}{3}+\frac{2 \pi x}{5}\)) .When t= 1, show that the formula can be rewritten as y = −A cos \(\frac{2 \pi x}{5}\).
Answer:
A cos (\(\frac{2 \pi t}{3}-\frac{2 \pi x}{5}\)) + A cos (\(\frac{2 \pi t}{3}+\frac{2 \pi x}{5}\)) = -A cos\(\frac { 2πx }{ 5 } \)
Explanation:
A standing wave can be modeled by the formula
y = A cos (\(\frac{2 \pi t}{3}-\frac{2 \pi x}{5}\)) + A cos (\(\frac{2 \pi t}{3}+\frac{2 \pi x}{5}\))
Let’s verify for t = 1
A cos (\(\frac{2 \pi}{3}-\frac{2 \pi x}{5}\)) + A cos (\(\frac{2 \pi}{3}+\frac{2 \pi x}{5}\)) = -Acos\(\frac { 2πx }{ 5 } \)
A cos (\(\frac{2 \pi}{3}-\frac{2 \pi x}{5}\)) = A. (cos\(\frac{2 \pi}{3}\) cos\(\frac { 2πx }{ 5 } \) + sin\(\frac{2 \pi}{3}\) sin\(\frac { 2πx }{ 5 } \))
= A . ((\(\frac { -1 }{ 2 } \)) . cos\(\frac { 2πx }{ 5 } \) + \(\frac { √3 }{ 2 } \) . sin\(\frac { 2πx }{ 5 } \))
= \(\frac { -1 }{ 2 } \)A cos\(\frac { 2πx }{ 5 } \) + \(\frac { √3 }{ 2 } \) A sin\(\frac { 2πx }{ 5 } \)
A cos(\(\frac { 2π }{ 5 } \) + \(\frac { 2πx }{ 3 } \)) = A(cos \(\frac { 2π }{ 5 } \) cos\(\frac { 2πx }{ 3 } \) – sin\(\frac { 2π }{ 5 } \) sin\(\frac { 2πx }{ 3 } \)
= A(-0.5 cos\(\frac { 2πx }{ 3 } \) – \(\frac { √3 }{ 2 } \) sin \(\frac { 2πx }{ 3 } \)
= –\(\frac { 1 }{ 2 } \)Acos\(\frac { 2πx }{ 3 } \) – \(\frac { √3 }{ 2 } \) A sin \(\frac { 2πx }{ 3 } \)
A cos (\(\frac{2 \pi t}{3}-\frac{2 \pi x}{5}\)) + A cos (\(\frac{2 \pi t}{3}+\frac{2 \pi x}{5}\)) = \(\frac { -1 }{ 2 } \)A cos\(\frac { 2πx }{ 5 } \) + \(\frac { √3 }{ 2 } \) A sin\(\frac { 2πx }{ 5 } \) – \(\frac { 1 }{ 2 } \)Acos\(\frac { 2πx }{ 3 } \) – \(\frac { √3 }{ 2 } \) A sin \(\frac { 2πx }{ 3 } \)
= -A cos\(\frac { 2πx }{ 5 } \)
Question 37.
MODELING WITH MATHEMATICS
The busy signal on a touch-tone phone is a combination of two tones with frequencies of 480 hertz and 620 hertz. The individual tones can be modeled by the equations:
480 hertz: y1 = cos 960πt
620 hertz: y2 = cos 1240πt
The sound of the busy signal can be modeled by y1 + y2. Show that y1 + y2 = 2 cos 1100πt cos 140πt.
Answer:

Question 38.
HOW DO YOU SEE IT?
Explain how to use the figure to solve the equation sin (x + \(\frac{\pi}{4}\)) − sin (\(\frac{\pi}{4}\) − x) = 0 for 0 ≤ x < 2π.
Answer:
The solutions of the equation are intersects points of the functions f(x) and g(x).
Explanation:
f(x) – g(x) = 0
From the graph, the points of intersection represent the points on the axis k where the functions f(k) and g(k) have the same values, f(x) = g(x), which means that these points will be solutions of our equation. From the graph, the intersects points and solutions of the equation on the interval 0 ≤ x ≤ 2π are
x = 0, x = π
Question 39.
MATHEMATICAL CONNECTIONS
The figure shows the acute angle of intersection, θ2 − θ1, of two lines with slopes m1 and m2.
a. Use the difference formula for tangent to write an equation for tan (θ2 − θ1) in terms of m1 and m2.
b. Use the equation from part (a) to find the acute angle of intersection of the lines y = x− 1 and y = \(\left(\frac{1}{\sqrt{3}-2}\right)\)x + \(\frac{4-\sqrt{3}}{2-\sqrt{3}}\).
Answer:

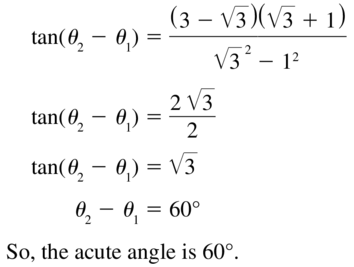
Question 40.
THOUGHT PROVOKING
Rewrite each function. Justify your answers.
a. Write sin 3x as a function of sin x.
b. Write cos 3x as a function of cos x.
c. Write tan 3x as a function of tan x.
Answer:
a. sin3x = 3sinx – 4sin³x
b. cos3x = 4cos³x – 3cosx
c. tan3x = \(\frac { 3tanx – tan³x }{ 1 – 3tan²x } \)
Explanation:
a. Sin 3x = sin(x + 2x)
= sinx cos2x + sin2x cosx
cos2x = cos(x +x)
= cosx . cosx – sinx . sinx
= cos²x – sin²x
sin2x = sin(x + x)
= sinx cosx + cosx sinx
= 2sinxcosx
sin3x = sinx cos2x + sin2x cosx
= sinx(cos²x – sin²x) + 2sinxcosx . cosx
= sinx(1 – sin²x – sin²x) + 2sinx cos²x
= sinx – 2sin³x + 2sinx . (1 – sin²x)
= sinx – 2sin³x + 2sinx – 2sin³x
= 3sinx – 4sin³x
b. y = cos3x
cos3x = cos(x + 2x)
= cosx cos2x + sin2x sinx
cos2x = cos(x +x)
= cosx . cosx – sinx . sinx
= cos²x – sin²x
sin2x = sin(x + x)
= sinx cosx + cosx sinx
= 2sinxcosx
cos3x = cosx cos2x – sin2x sinx
= cosx (cos²x – sin²x) – 2sinxcosx . sinx
= cosx (cos²x – 1 + cos²x) – 2cosx(1 – cos²x)
= 2cos³x – cosx – 2cosx + 2cos³x
= 4cos³x – 3cosx
c. y = tan3x
tan3x = tan(x + 2x)
= \(\frac { tanx + tan2x }{ 1 – tanx tan2x } \)
tan2x = \(\frac { tanx + tanx }{ 1 – tan²x } \)
= \(\frac { 2tanx }{ 1 – tan²x } \)
tanx = \(\frac { tanx + (2tanx / (1 – tan²x)) }{ 1 – tanx (2tanx / (1 – tan²x) } \)
= \(\frac { 3tanx – tan³x }{ 1 – 3tan²x } \)
Maintaining Mathematical Proficiency
Solve the equation. Check your solution(s).
Question 41.
1 − \(\frac{9}{x-2}\) = −\(\frac{7}{2}\)
Answer:

Question 42.
\(\frac{12}{x}\) + \(\frac{3}{4}\) = \(\frac{8}{x}\)
Answer:
The solution of the equation is x = \(\frac { -16 }{ 3 } \)
Explanation:
\(\frac { 12 }{ x } \) + \(\frac { 3 }{ 4 } \) = \(\frac { 8 }{ x } \)
\(\frac { 12 }{ x } \) – \(\frac { 8 }{ x } \) = –\(\frac { 3 }{ 4 } \)
\(\frac { 12 – 8 }{ x } \) = –\(\frac { 3 }{ 4 } \)
\(\frac { 4 }{ x } \) = –\(\frac { 3 }{ 4 } \)
16 = -3x
x = \(\frac { -16 }{ 3 } \)
Question 43.
\(\frac{2 x-3}{x+1}\) = \(\frac{10}{x^{2}-1}\) + 5
Answer:


Trigonometric Ratios and Functions Performance Task: Lightening the Load
9.5–9.8 What Did You Learn?
Core Vocabulary
frequency, p. 506
sinusoid, p. 507
trigonometric identity, p. 514
Core Concepts
Section 9.5
Characteristics of y = tan x and y = cot x, p. 498
Period and Vertical Asymptotes of y = a tan bx and y = a cot bx, p. 499
Characteristics of y = sec x and y = csc x, p. 500
Section 9.6
Frequency, p. 506
Writing Trigonometric Functions, p. 507
Using Technology to Find Trigonometric Models, p. 509
Section 9.7
Fundamental Trigonometric Identities, p. 514
Section 9.8
Sum and Difference Formulas, p. 520
Trigonometric Equations and Real-Life Formulas, p. 522
Mathematical Practices
Question 1.
Explain why the relationship between θ and d makes sense in the context of the situation in Exercise 43 on page 503.
Answer:
Question 2.
How can you use definitions to relate the slope of a line with the tangent of an angle in Exercise 39 on page 524?
Answer:
Performance Task: Lightening the Load
You need to move a heavy table across the room. What is the easiest way to move it? Should you push it? Should you tie a rope around one leg of the table and pull it? How can trigonometry help you make the right decision?
To explore the answers to these questions and more, go to BigIdeasMath.com.

Trigonometric Ratios and Functions Chapter Review
9.1 Right Triangle Trigonometry (pp. 461−468)
Question 1.
In a right triangle, θ is an acute angle and cos θ = \(\frac{6}{11}\). Evaluate the other five trigonometric functions of θ.
Answer:
sin θ = \(\frac { √85 }{ 11 } \)
tan θ = \(\frac { √85 }{ 6 } \)
cot θ = \(\frac { 6}{ √85 } \)
sec θ = \(\frac { 11 }{ 6 } \)
csc θ =\(\frac { 11 }{ √85 } \)
Explanation:
cos θ = \(\frac{6}{11}\)
adj side = 6, hypotenuse = 11
opposite side = √85
sin θ = \(\frac { opposite side }{ hypotenuse } \) = \(\frac { √85 }{ 11 } \)
tan θ = \(\frac { opp side }{ adj side } \) = \(\frac { √85 }{ 6 } \)
cot θ = \(\frac { adj side }{ opp side} \) = \(\frac { 6}{ √85 } \)
sec θ = \(\frac { hypotenuse }{ adj side } \) = \(\frac { 11 }{ 6 } \)
csc θ = \(\frac { hyp }{ opp side } \) = \(\frac { 11 }{ √85 } \)
Question 2.
The shadow of a tree measures 25 feet from its base. The angle of elevation to the Sun is 31°. How tall is the tree?
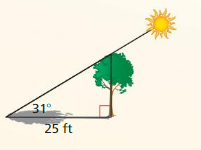
Answer:
The height of the tree is 15 ft
Explanation:
tan 31° = \(\frac { h }{ 25 } \)
0.6 = \(\frac { h }{ 25 } \)
h = 25 x 0.6
h = 15
9.2 Angles and Radian Measure (pp. 469−476)
Question 3.
Find one positive angle and one negative angle that are coterminal with 382°.
Answer:
382 – 360 = 22
22 – 360 = -338
The coterminal angles are -338°, 22°
Convert the degree measure to radians or the radian measure to degrees.
Question 4.
30°
Answer:
30° = 30° x \(\frac { π }{ 180° } \)
= \(\frac { π }{ 6 } \)
Question 5.
225°
Answer:
225° = 225° x \(\frac { π }{ 180° } \)
= \(\frac { 5π }{ 4 } \)
Question 6.
\(\frac{3 \pi}{4}\)
Answer:
\(\frac{3 \pi}{4}\) = \(\frac{3 \pi}{4}\) x \(\frac {180° }{ π } \)
= 135°
Question 7.
\(\frac{5 \pi}{3}\)
Answer:
\(\frac{5 \pi}{3}\) = \(\frac{5 \pi}{3}\) x \(\frac {180° }{ π } \)
= 300°
Question 8.
A sprinkler system on a farm rotates 140°and sprays water up to 35 meters. Draw a diagram that shows the region that can be irrigated with the sprinkler. Then find the area of the region.
Answer:
The area of the region is 1497 m²
Explanation:
140° = 140° x \(\frac { π }{ 180° } \)
= \(\frac { 7π }{ 9 } \)
Area = 0.5r²θ
r = 35
A = 0.5 x 35² x \(\frac { 7π }{ 9 } \)
= 1497
9.3 Trigonometric Functions of Any Angle (pp. 477−484)
Evaluate the six trigonometric functions of θ.
Question 9.
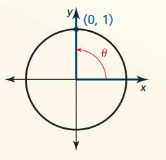
Answer:
sin θ = 1
cos θ = 0
tan θ = undefined
cot θ = 0
sec θ = undefined
csc θ = 1
Explanation:
sin θ = \(\frac { y }{ r } \) = \(\frac { 1 }{ 1 } \)
cos θ = = \(\frac { x }{ r } \) = \(\frac { 0 }{ 1 } \) = 0
tan θ = \(\frac { y }{ x } \) = \(\frac { 1 }{ 0 } \) = undefined
cot θ = = \(\frac { x }{ y } \) = \(\frac { 0 }{ 1 } \) = 0
sec θ = \(\frac { r }{ x } \) = \(\frac { 1 }{ 0 } \) = undefined
csc θ = \(\frac { r }{ y } \) = \(\frac { 1 }{ 1 } \) = 1
Question 10.
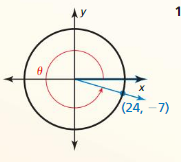
Answer:
sin θ = \(\frac { -7 }{ 25 } \)
cos θ = \(\frac { 24 }{ 25 } \)
tan θ = \(\frac { -7 }{ 24 } \)
cot θ = \(\frac { -24 }{ 7 } \)
sec θ =\(\frac { 25 }{ 24 } \)
csc θ = \(\frac { -25 }{ 7 } \)
Explanation:
sin θ = \(\frac { y }{ r } \) = \(\frac { -7 }{ 25 } \)
cos θ = = \(\frac { x }{ r } \) = \(\frac { 24 }{ 25 } \)
tan θ = \(\frac { y }{ x } \) = \(\frac { -7 }{ 24 } \)
cot θ = = \(\frac { x }{ y } \) = \(\frac { -24 }{ 7 } \)
sec θ = \(\frac { r }{ x } \) = \(\frac { 25 }{ 24 } \)
csc θ = \(\frac { r }{ y } \) = \(\frac { -25 }{ 7 } \)
Question 11.
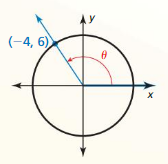
Answer:
sin θ = \(\frac { 3 }{ √13 } \)
cos θ = \(\frac { -2 }{ √13 } \)
tan θ = \(\frac { -3 }{ 2 } \)
cot θ = \(\frac { -2 }{ 3 } \)
sec θ =\(\frac { -√13 }{ 2 } \)
csc θ = \(\frac { √13 }{ 3 } \)
Explanation:
sin θ = \(\frac { y }{ r } \) = \(\frac { 6 }{ 2√13 } \)
cos θ = = \(\frac { x }{ r } \) = \(\frac { -4 }{ 2√13 } \)
tan θ = \(\frac { y }{ x } \) = \(\frac { 6 }{ -4 } \)
cot θ = = \(\frac { x }{ y } \) = \(\frac { -4 }{ 6 } \)
sec θ = \(\frac { r }{ x } \) = \(\frac { 2√13 }{ -4 } \)
csc θ = \(\frac { r }{ y } \) = \(\frac { 2√13}{ 6 } \)
Evaluate the function without using a calculator.
Question 12.
tan 330°
Answer:
tan 330° = \(\frac { -√3 }{ 3 } \)
Explanation:
θ = 330
θ’ = 360 – 330 = 30
tan 330° = -tan30 = \(\frac { -√3 }{ 3 } \)
Question 13.
sec(−405°)
Answer:
sec(−405°) = √2
Explanation:
θ = -405
720 – 405 = 315
θ’ = 360 – 315 = 45
sec(-405) = sec 45 = √2
Question 14.
sin \(\frac{13 \pi}{6}\)
Answer:
sin \(\frac{13 \pi}{6}\) = \(\frac { 1 }{ 2 } \)
Explanation:
θ = \(\frac{13 \pi}{6}\)
θ’ = \(\frac{13 \pi}{6}\) – 2π = \(\frac { π }{ 6 } \)
sin \(\frac{13 \pi}{6}\) = sin\(\frac { π }{ 6 } \) = \(\frac { 1 }{ 2 } \)
Question 15.
sec \(\frac{11 \pi}{3}\)
Answer:
sec \(\frac{11 \pi}{3}\) = 2
Explanation:
θ = \(\frac{11 \pi}{3}\)
θ’ = 4π – \(\frac{11 \pi}{3}\) = \(\frac { π }{ 3 } \)
sec \(\frac{11 \pi}{3}\) = sec\(\frac { π }{ 3 } \) = 2
9.4 Graphing Sine and Cosine Functions (pp. 485−494)
Identify the amplitude and period of the function. Then graph the function and describe the graph of g as a transformation of the graph of the parent function.
Question 16.
g(x) = 8 cos x
Answer:
Amplitude = 8, period is 2π
Explanation:
g(x) = 8 cos x
Amplitude = |8| = 8
Period = \(\frac { 2π }{ 1 } \) = 2π
Question 17.
g(x) = 6 sin πx
Answer:
Amplitude = 6, period is 2
Explanation:
g(x) = 6 sin πx
Amplitude = |6| = 6
Period = \(\frac { 2π }{ π } \) = 2
Question 18.
g(x) = \(\frac{1}{4}\) cos 4x
Answer:
Amplitude = \(\frac{1}{4}\), period is \(\frac { π }{ 2 } \)
Explanation:
g(x) = \(\frac{1}{4}\) cos 4x
Amplitude = |\(\frac{1}{4}\)| = \(\frac{1}{4}\)
Period = \(\frac { 2π }{ 4 } \) = \(\frac { π }{ 2 } \)
Graph the function.
Question 19.
g(x) = cos(x + π) + 2
Answer:
Explanation:
g(x) = cos(x + π) + 2
a = 1, b = 1, h = -π, k = 2
amplitude = 1
Period = 2π
Midline: y = 2
Vertical shift = 2
Horizontal shift = -π
the intersect points of the function with midline is (\(\frac { π }{ 2 } \) – π, 2) = (\(\frac { -π }{ 2 } \), 3)
since the period is 2π, we will draw the points (\(\frac { -π }{ 2 } \) + kπ, 2)
maximum = (π, 3)
minimum = (0, 1)
Question 20.
g(x) = −sin x − 4
Answer:
Explanation:
g(x) = −sin x − 4
a = -1, b = 1, h = 0, k = -4
amplitude = |-1| = 1
Period = 2π
Midline: y = -4
Vertical shift = -4
Horizontal shift = 0
−sin x − 4 = 0
sinx = -4
So, the equation has no solution
the intersect points of the function with midline is (0, -4), (π, -4)
maximum = (\(\frac { π }{ 8 } \), -3)
minimum = (\(\frac { 3π }{ 8 } \), -1)
Question 21.
g(x) = 2 sin (x + \(\frac{\pi}{2}\))
Answer:
Explanation:
g(x) = 2 sin (x + \(\frac{\pi}{2}\))
a = 2, b = 1, h = –\(\frac { π }{ 2 } \), k = 0
amplitude = |2| = 1
Period = 2π
Midline: y = 0
Vertical shift = 0
Horizontal shift = –\(\frac { π }{ 2 } \)
the intersect points of the function with midline is (-\(\frac { π }{ 2 } \), 0), (\(\frac { π }{ 2 } \), 0)
maximum = (0, 2)
minimum = (π, -2)
9.5 Graphing Other Trigonometric Functions (pp. 497−504)
Graph one period of the function. Describe the graph of g as a transformation of the graph of its parent function.
Question 22.
g(x) = tan \(\frac{1}{2}\)x
Answer:
Explanation:
g(x) = tan \(\frac{1}{2}\)x
a = 2, b = 0.5
Period = 2π
The x-intercepts are (2kπ, 2kπ)
the halfway points are (\(\frac { π }{ 2 } \), 1) and (-\(\frac { π }{ 2 } \), -1)
The vertical asymptotes are x = π, x = -π
Question 23.
g(x) = 2 cot x
Answer:
Explanation:
g(x) = 2 cot x
a = 2, b = 1
Period = π
The x-intercepts are (\(\frac { π }{ 2 } \) + 2kπ, 0)
the halfway points are (\(\frac { π }{ 4 } \), 2) and (-\(\frac { 3π }{ 4 } \), -2)
The vertical asymptotes are x = 0, x = -π
Question 24.
g(x) = 4 tan 3πx
Answer:
Explanation:
g(x) = 4 tan 3πx
a = 4, b = 3π
Period = \(\frac { 1 }{ 3 } \)
The x-intercepts are (\(\frac { 1 }{ 3 } \), \(\frac { 1 }{ 3 } \))
the halfway points are (\(\frac { 1 }{ 12 } \), 4) and (-\(\frac { 1 }{ 3 } \), -4)
The vertical asymptotes are x = \(\frac { 1 }{ 6 } \), x = –\(\frac { 1 }{ 6 } \)
Graph the function.
Question 25.
g(x) = 5 csc x
Answer:
Explanation:
g(x) = 5 csc x
First, let’s graph the function f(x) = 5sinx. The graph of f(x) represent a vertically strech by a factor 5 of function sinx. The period is 2π, amplitude is 5, midline is x-axis. The x-intercepts are points form of xk = kπ
Maximum = (\(\frac { π }{ 2 } \) + 2kπ, 5)
Minimum = (\(\frac { 3π }{ 2 } \) + 2kπ, -5)
Let’s graph the asymptotes of the function g(x). Because the asymptotes of g(x) occur when 5sinx = 0
x = 0, x = π, x = -π
Now, let’s plot the points where f(x) = 5sinx reaches maximum & minimum value. These points are (\(\frac { π }{ 2 } \), 5), (-\(\frac { π }{ 2 } \), -5)
Question 26.
g(x) = sec \(\frac{1}{2}\)x
Answer:
Explanation:
g(x) = sec \(\frac{1}{2}\)x
First, let’s graph the function f(x) = cos\(\frac{1}{2}\)x. The graph of f(x) represent a horizontally strech by a factor 2 of function cosx. The period is 4π, amplitude is 1, midline is x-axis. The x-intercepts are points form of xk = π + 2kπ
Maximum = (0, 1)
Minimum = (2π, -1)
Let’s graph the asymptotes of the function g(x). Because the asymptotes of g(x) occur when cos\(\frac{1}{2}\)x = 0
x = π, x = 3π
Now, let’s plot the points where f(x) = cos\(\frac{1}{2}\)x reaches maximum & minimum value. These points are (0, 1), (2π, -1)
Question 27.
g(x) = 5 sec πx
Answer:

Explanation:
g(x) = 5 sec πx
First, let’s graph the function f(x) = 5cosπx. The graph of f(x) represent a vertically shrink by a factor 5 of function cosx. The period is 2, amplitude is 0.5, midline is x-axis. The x-intercepts are points form of xk = 0.5 + 2k
Maximum = (0, 5)
Minimum = (1, -5)
Let’s graph the asymptotes of the function g(x). Because the asymptotes of g(x) occur when 5cosπx = 0
x = 0.5, x = -0.5
Now, let’s plot the points where f(x) = 5cosπx reaches maximum & minimum value. These points are (0, 5), (1, -5)
Question 28.
g(x) = \(\frac{1}{2}\) csc \(\frac{\pi}{4}\)x
Answer:
Explanation:
g(x) = \(\frac{1}{2}\) csc \(\frac{\pi}{4}\)x
First, let’s graph the function f(x) = \(\frac{1}{2}\) sin \(\frac{\pi}{4}\)x. The graph of f(x) represent a vertically shrink by a factor 0.5 of function sinx. The period is 8, amplitude is 0.5, midline is x-axis. The x-intercepts are points form of xk = 4k
Maximum = (2 + 8k, \(\frac{1}{2}\))
Minimum = (-2 + 8k, –\(\frac{1}{2}\))
Let’s graph the asymptotes of the function g(x). Because the asymptotes of g(x) occur when \(\frac{1}{2}\) sin \(\frac{\pi}{4}\)x = 0
x = 0, x = 4, x = -4
Now, let’s plot the points where f(x) = \(\frac{1}{2}\) sin \(\frac{\pi}{4}\)x reaches maximum & minimum value. These points are (2, 0.5), (-2, -0.5)
9.6 Modeling with Trigonometric Functions (pp. 505−512)
Write a function for the sinusoid.
Question 29.
Answer:
g(x) = -sin\(\frac{1}{2}\)x
Question 30.
Answer:
g(x) = cosπx – 2
Question 31.
You put a reflector on a spoke of your bicycle wheel. The highest point of the reflector is 25 inches above the ground, and the lowest point is 2 inches. The reflector makes 1 revolution per second. Write a model for the height h (in inches) of a reflector as a function of time t (in seconds) given that the reflector is at its lowest point when t = 0.
Answer:
y = -11.5 cos2πx + 13.5
Explanation:
fmax = 25, fmin = 2
k = \(\frac { 25 + 2 }{ 2 } \)
= 13.5
b = 2π
|a| = \(\frac { 25 – 2 }{ 2 } \)
= 11.5
y = -11.5cos2π(x – 0) + 13.5 = -11.5 cos2πx + 13.5
Question 32.
The table shows the monthly precipitation P (in inches) for Bismarck, North Dakota, where t = 1 represents January. Write a model that gives P as a function of t and interpret the period of its graph.

Answer:
p(t) = 1.0764 sin(0.585t + 3.954) + 1.528
Explanation:
Make a scatter plot of the data
The curve seems sinusoidal, so we perform sinusoidal regression
y = 1.0764 sin(0.585t + 3.954) + 1.528
The period = 12
9.7 Using Trigonometric Identities (pp. 513−518)
Simplify the expression.
Question 33.
cot2x − cot2x cos2x
Answer:
cot2x − cot2x cos2x = cos²x
Explanation:
cot2x − cot2x cos2x = cot²x – cot²x(1 – sin²x)
= cot²x – cot²x + cot²x . sin²x
= \(\frac { cos²x }{ sin²x } \) . sin²x
= cos²x
Question 34.
\(\frac{(\sec x+1)(\sec x-1)}{\tan x}\)
Answer:
\(\frac{(\sec x+1)(\sec x-1)}{\tan x}\) = tanx
Explanation:
\(\frac{(\sec x+1)(\sec x-1)}{\tan x}\) = \(\frac { (1/cosx + 1)(1/cosx – 1) }{ sinx/cosx } \)
= \(\frac { (1 + cosx)/cosx . (1 – cosx)/cosx }{ sinx/cosx } \)
= \(\frac { (1 – cos²x)/cos²x }{ sinx/cosx } \)
= \(\frac { sin²x/cos²x }{ sinx/cosx } \)
= \(\frac { sin²x . cosx }{ cos²x . sinx } \)
= \(\frac { sin x }{ cos x } \)
= tanx
Question 35.
sin (\(\frac{\pi}{2}\) − x)tan x
Answer:
sin (\(\frac{\pi}{2}\) − x)tan x = sinx
Explanation:
sin (\(\frac{\pi}{2}\) − x) = cosx
tanx = \(\frac { sin x }{ cos x } \)
sin (\(\frac{\pi}{2}\) − x)tan x = cosx. \(\frac { sin x }{ cos x } \)
= sinx
Verify the identity.
Question 36.
\(\frac{\cos x \sec x}{1+\tan ^{2} x}\) = cos2x
Answer:
\(\frac{\cos x \sec x}{1+\tan ^{2} x}\) = \(\frac { cosx . (1/cosx) }{ 1 + sinx/cosx } \)
= \(\frac { 1 }{ (cos²x + sin²x)/cos²x } \)
= \(\frac { 1 }{ 1/cos²x } \)
= cos²x
Question 37.
tan (\(\frac{\pi}{2}\) − x)cot x = csc2x − 1
Answer:
tan (\(\frac{\pi}{2}\) − x) = cotx
tan (\(\frac{\pi}{2}\) − x)cot x = cotx . cotx
= cot²x
= \(\frac { cos²x }{ sin²x } \)
= \(\frac { 1 – sin²x }{ sin²x } \)
= \(\frac { 1 }{ sin²x } \) – \(\frac { sin²x }{ sin²x } \)
= csc²x – 1
9.8 Using Sum and Difference Formulas (pp. 519−524)
Find the exact value of the expression.
Question 38.
sin 75°
Answer:
sin 75° = \(\frac { √6 + √2 }{ 4 } \)
Explanation:
sin 75° = sin(45 + 30)
= sin45 cos30 + sin30 cos45
= \(\frac { √2 }{ 2 } \) . \(\frac { √3 }{ 2 } \) + \(\frac { 1 }{ 2 } \) . \(\frac { √2 }{ 2 } \)
= \(\frac { √6 }{ 4 } \) + \(\frac { √2 }{ 4 } \)
= \(\frac { √6 + √2 }{ 4 } \)
Question 39.
tan(−15°)
Answer:
tan(−15°) = -2 + √3
Explanation:
tan(−15°) = tan(30 – 45)
= \(\frac { tan30 – tan45 }{ 1 + tan30 tan45 } \)
= \(\frac { √3/3 – 1 }{ 1 + √3/3 . 1 } \)
= \(\frac { (√3 – 3)/3 }{ (3 + √3)/3 } \)
= \(\frac { √3 – 3 }{ √3 + 3 } \)
= \(\frac { ( √3 – 3)(√3 – 3) }{ (√3 + 3)(√3 – 3) } \)
= \(\frac { 3 – 6√3 + 9 }{ -6 } \)
= \(\frac { 12 – 6√3 }{ 6 } \)
= -2 + √3
Question 40.
cos \(\frac{\pi}{12}\)
Answer:
cos \(\frac{\pi}{12}\) = \(\frac { √2 + √6 }{ 4 } \)
Explanation:
cos \(\frac{\pi}{12}\) = cos(\(\frac { π }{ 3 } \) – \(\frac { π }{ 4 } \))
= cos\(\frac { π }{ 3 } \)cos\(\frac { π }{ 4 } \) + sin\(\frac { π }{ 3 } \)sin\(\frac { π }{ 4 } \)
= \(\frac { 1 }{ 2 } \) . \(\frac { √2 }{ 2 } \) + \(\frac { √2 }{ 2 } \) . \(\frac { √3 }{ 2 } \)
= \(\frac { √2 + √6 }{ 4 } \)
Question 41.
Find tan(a + b), given that tan a = \(\frac{1}{4}\) with π < a < \(\frac{3 \pi}{2}\) and tan b = \(\frac{3}{7}\) with 0 < b < \(\frac{\pi}{2}\) .
Answer:
tan(a + b) = \(\frac { 19 }{ 25 } \)
Explanation:
tan a = \(\frac { 1 }{ 4 } \)
tan b = \(\frac { 3 }{ 7 } \)
tan(a + b) = \(\frac { 1/4 + 3/7 }{ 1 – (1/4 . 3/7) } \)
= \(\frac { 7/28 + 12/28 }{ 1 – 3/28 } \)
= \(\frac { 19/28 }{ 25/28 } \)
= \(\frac { 19 }{ 25 } \)
Solve the equation for 0 ≤ x < 2π.
Question 42.
cos (x + \(\frac{3 \pi}{4}\)) + cos (x − \(\frac{3 \pi}{4}\)) = 1
Answer:
The solutions of the equation are x = \(\frac { 3π }{ 4 } \), x = \(\frac { 5π }{ 4 } \)
Explanation:
The interval is 0 < x < 2π
cos (x + \(\frac{3 \pi}{4}\)) + cos (x − \(\frac{3 \pi}{4}\)) = 1
cos (x + \(\frac{3 \pi}{4}\)) = cosx . cos\(\frac{3 \pi}{4}\) – sinx . sin\(\frac{3 \pi}{4}\)
= cosx . \(\frac { -√2 }{ 2 } \) – sinx . \(\frac { √2 }{ 2 } \)
= –\(\frac { √2 }{ 2 } \)cosx – \(\frac { √2 }{ 2 } \)sinx
cos (x − \(\frac{3 \pi}{4}\)) = cosx cos\(\frac{3 \pi}{4}\) + sinx sin\(\frac{3 \pi}{4}\)
= cosx . \(\frac { -√2 }{ 2 } \) + sinx. \(\frac { √2 }{ 2 } \)
= \(\frac { -√2 }{ 2 } \)cosx + \(\frac { √2 }{ 2 } \)sinx
–\(\frac { √2 }{ 2 } \)cosx – \(\frac { √2 }{ 2 } \)sinx – \(\frac { √2 }{ 2 } \)cosx + \(\frac { √2 }{ 2 } \)sinx = 1
-2 . \(\frac { √2 }{ 2 } \)cosx = 1
cosx = –\(\frac { √2 }{ 2 } \)cosx
cos\(\frac { π }{ 4 } \) = \(\frac { √2 }{ 2 } \)
cos(π – x) = -cosx
cos(π + x) = -cosx
The solutions of the equation are
x = π – \(\frac { π }{ 4 } \) = \(\frac { 3π }{ 4 } \)
x = π + \(\frac { π }{ 4 } \) = \(\frac { 5π }{ 4 } \)
Question 43.
tan(x + π) + cos (x + \(\frac{\pi}{2}\))= 0
Answer:
The solutions of the equations are x = 0 , x = π
Explanation:
tan(x + π) + cos (x + \(\frac{\pi}{2}\))= 0
tan(x + π) = \(\frac { tanx + tanπ }{ 1 – tanx tanπ } \)
= \(\frac { tanx + 0 }{ 1 – tanx . 0 } \)
= tanx
cos (x + \(\frac{\pi}{2}\)) = cosx cos\(\frac{\pi}{2}\) – sinx sin\(\frac{\pi}{2}\)
= cosx . 0 – sinx. 1
= -sinx
tan(x + π) + cos (x + \(\frac{\pi}{2}\)) = 0
tanx – sinx = 0
tanx = sinx
\(\frac { sinx }{ cosx } \) = sinx
The solutions of the equations are x = 0 , x = π
Trigonometric Ratios and Functions Chapter Test
Verify the identity.
Question 1.
\(\frac{\cos ^{2} x+\sin ^{2} x}{1+\tan ^{2} x}\) = cos2x
Answer:
\(\frac{\cos ^{2} x+\sin ^{2} x}{1+\tan ^{2} x}\) = \(\frac { 1 }{ 1 + sin²x/cos²x } \)
= \(\frac { 1 }{ (cos²x + sin²x) / cos²x } \)
= \(\frac { cos²x }{ 1 } \)
= cos²x
Question 2.
\(\frac{1+\sin x}{\cos x}+\frac{\cos x}{1+\sin x}\) = 2 sec x
Answer:
\(\frac{1+\sin x}{\cos x}+\frac{\cos x}{1+\sin x}\) = \(\frac { (1 + sinx)² }{ cosx(1 + sinx) } \) + \(\frac { cos²x }{ (1 + sinx)cosx } \)
= \(\frac { 1 + 2sinx + sin²x }{ cosx(1 + sinx) } \) + \(\frac { cos²x }{ cosx(1 + sinx) } \)
= \(\frac { 1 + 2sinx + sin²x + cos²x }{ (1 + sinx)cosx } \)
= \(\frac { 2 + 2sinx }{ (1 + sinx)cosx } \)
= \(\frac { 2(1 + sinx) }{ (1 + sinx)cosx } \)
= 2 . \(\frac { 1 }{ cosx } \)
= 2 secx
Question 3.
cos (x + \(\frac{3 \pi}{2}\)) = sin x
Answer:
cos (x + \(\frac{3 \pi}{2}\)) = cosx cos\(\frac{3 \pi}{2}\) – sinx sin\(\frac{3 \pi}{2}\)
= cosx . 0 – sinx (-1)
= sinx
Question 4.
Evaluate sec(−300°) without using a calculator.
Answer:
sec(−300°) = 2
Explanation:
θ = -300
θ’ = 360 – 300 = 60
sec(−300°) = sec60 = \(\frac { 1 }{ cos60 } \)
= \(\frac { 1 }{ 0.5 } \) = 2
Write a function for the sinusoid.
Question 5.
Answer:
y = 3cosπx + 2
Explanation:
fmax = 5, fmin = -1
k = \(\frac { 5 – 1 }{ 2 } \) = 2
by using the period, b = π
|a| = \(\frac { 5 – (-1) }{ 2 } \) = 3
y = 3cos(π(x – 0)) + 2 = 3cosπx + 2
Question 6.
Answer:
y = -3sin\(\frac { 4 }{ 3 } \)x – 2
Explanation:
fmax = 1, fmin = -1
k = \(\frac { 1 + 1 }{ 2 } \) = 1
by using the period, b = \(\frac { 4 }{ 3 } \)
|a| = \(\frac { 1 + 1 }{ 2 } \) = 1
y = -3sin\(\frac { 4 }{ 3 } \)x – 2
Graph the function. Then describe the graph of g as a transformation of the graph of its parent function.
Question 7.
g(x) = −4 tan 2x
Answer:

Explanation:
g(x) = −4 tan 2x
a = -4, b = 2
period = \(\frac { π }{ b } \) = \(\frac { π }{ 2 } \)
The x-intercepts are (0 + \(\frac { kπ }{ 2 } \), 0 + \(\frac { kπ }{ 2 } \)) = (\(\frac { kπ }{ 2 } \), \(\frac { kπ }{ 2 } \))
The halfway points are
(\(\frac { π }{b } \), -a) = (\(\frac { π }{8 } \), -4)
(-\(\frac { π }{b } \), a) = (-\(\frac { π }{8} \), 4)
The vertical asymptotoes are x = \(\frac { π }{ 4} \)
x = \(\frac { -π }{ 4} \)
Question 8.
g(x) = −2 cos \(\frac{1}{3}\)x + 3
Answer:
Explanation:
g(x) = −2 cos \(\frac{1}{3}\)x + 3
a = -2, b = 1/3, h = 0, k = 3
amplitude = |-2| = 2
Period = \(\frac { 2π }{ b } \) = 6π
Midline y = 3
Vertical shift = 3
Horizontal shift = 0
The intersect points of the midline is \(\frac { 2π }{ b } \), 3) = (\(\frac { 3π }{ 2 } \), 3)
Maximum = (\(\frac { 2π }{ b } \), k + a) = (6π, 5)
Minimum = (\(\frac { π }{ b } \), k – a) = (3π, 1)
Because a = -2 < 0, the graph is reflected in the midline y = 3
(6π, 5) becomes (6π, 1) (minimum)
(3π, 1) becomes (3π, 5) (maximum
Question 9.
g(x) = 3 csc πx
Answer:
Explanation:
g(x) = 3 csc πx
The period is 2, amplitude = 3, midline is x-axis
The x-intercepts are xk = k
Maximum = (\(\frac { 1 }{ 2 } \) + 2k, 3)
Minimum = (\(\frac { 3 }{ 2 } \) + 2k, -3)
The asymptotoes of the function g(x) are x = 0, x = 1, x = 2
Plot the points f(x) = 3 sinπx reaches maximum and minimum value
(0.5, 3), (1.5, -3)
Convert the degree measure to radians or the radian measure to degrees. Then find one positive angle and one negative angle that are coterminal with the given angle.
Question 10.
−50°
Answer:
−50° = \(\frac { -5π }{ 18 } \)
Explanation:
−50° = -50 x \(\frac { π }{ 180 } \)
= \(\frac { -5π }{ 18 } \)
Question 11.
\(\frac{4 \pi}{5}\)
Answer:
\(\frac{4 \pi}{5}\) = 144°
Explanation:
\(\frac{4 \pi}{5}\) = \(\frac{4 \pi}{5}\) x \(\frac { 180 }{ π } \)
= 144°
Question 12.
\(\frac{8 \pi}{3}\)
Answer:
\(\frac{8 \pi}{3}\) = 480°
Explanation:
\(\frac{8 \pi}{3}\) = \(\frac{8 \pi}{3}\) x \(\frac { 180 }{ π } \)
= 480°
Question 13.
Find the arc length and area of a sector with radius r = 13 inches and central angle θ = 40°.
Answer:
The length of the sector is 9.08 in, area is 59 sq in
Explanation:
40 = 40 x \(\frac { π }{ 180 } \)
= \(\frac { 2π }{ 9 } \)
r = 13
Arc length = rθ
= 13 x \(\frac { 2π }{ 9 } \)
= 9.08
Area = 0.5r²θ
= 0.5 x 13² x \(\frac { 2π }{ 9 } \)
= 59
Evaluate the six trigonometric functions of the angle θ.
Question 14.
Answer:
sin θ = \(\frac { -9 }{ √85 } \)
cos θ = \(\frac { 2 }{ √85 } \)
tan θ = \(\frac { -9 }{ 2 } \)
cot θ = \(\frac { -2 }{ 9 } \)
sec θ = \(\frac { √85 }{ 2 } \)
csc θ = \(\frac { -√85}{ 9 } \)
Explanation:
x = 2, y= -9
r = √85
sin θ = \(\frac { y }{ r } \) = \(\frac { -9 }{ √85 } \)
cos θ = = \(\frac { x }{ r } \) = \(\frac { 2 }{ √85 } \)
tan θ = \(\frac { y }{ x } \) = \(\frac { -9 }{ 2 } \)
cot θ = = \(\frac { x }{ y } \) = \(\frac { -2 }{ 9 } \)
sec θ = \(\frac { r }{ x } \) = \(\frac { √85 }{ 2 } \)
csc θ = \(\frac { r }{ y } \) = \(\frac { -√85}{ 9 } \)
Question 15.

Answer:
sin θ = 0
cos θ = -1
tan θ = 0
cot θ =undefined
sec θ = -1
csc θ = undefined
Explanation:
x = -1, y= 0
r = 1
sin θ = \(\frac { y }{ r } \) = \(\frac { 0 }{ 1 } \) = 0
cos θ = = \(\frac { x}{ r } \) = \(\frac { -1 }{ 1 } \) = -1
tan θ = \(\frac { y }{ x } \) = \(\frac { 0 }{ -1 } \) = 0
cot θ = = \(\frac { x }{ y } \) = \(\frac { -1 }{ 0 } \) = undefined
sec θ = \(\frac { r }{ x } \) = \(\frac { 1 }{ -1 } \) = -1
csc θ = \(\frac { r }{ y } \) = \(\frac { 1}{ 0 } \) = undefined
Question 16.
In which quadrant does the terminal side of θ lie when cos θ < 0 and tan θ > 0? Explain.
Answer:
The angle θ lies in the third quadrant
Question 17.
How tall is the building? Justify your answer.
Answer:
The height of the building is 178 ft
Explanation:
sin 60° = \(\frac { H }{ 200 } \)
\(\frac { √3 }{ 2 } \) = \(\frac { H }{ 200 } \)
H = 173.2
The height of the building H = h – 5
173.2 + 5 = h
h =178
Question 18.
The table shows the average daily high temperatures T (in degrees Fahrenheit) in Baltimore, Maryland, where m= 1 represents January. Write a model that gives T as a function of m and interpret the period of its graph.

Answer:
The model is N(t) = 23.14sin(0.495x – 1.95) + 63.7
Explanation:
SinReg
a = 23.14, b = 0.495, c = -1.95, d = 63.7
N(t) = 23.14sin(0.495x – 1.95) + 63.7
T = 127
The period of the model is 12.7 months
Trigonometric Ratios and Functions Cumulative Assessment
Question 1.
Which expressions are equivalent to 1?

Answer:
cos²x + sin²x = 1
\(\frac { cos²(-x)tan²x }{ sin²(-x) } \) = 1
cos(\(\frac { π }{ 2 } \) -x)cscx = 1
Explanation:
sin(-x) = -sinx
cos(-x) = cosx
tanx = \(\frac { sinx }{ cosx } \)
cotx = \(\frac { cosx }{ sinx } \)
csc x = \(\frac { 1 }{ sinx } \)
secx = \(\frac { 1 }{ cosx } \)
cos(\(\frac { π }{ 2 } \) -x) = sinx
tanxsecxcosx = tanx . \(\frac { 1 }{ cosx } \) . cosx = tanx
which is not equal to 1
cos²x + sin²x = 1
Question 2.
Which rational expression represents the ratio of the perimeter to the area of the playground shown in the diagram?

Answer:
A
Explanation:
Perimeter = 2x + 6x + 3x + 2x + x + 4x = 18x
Area = 2x . 6x + 2x. x = 12x² + 12x² = 14x²
\(\frac { Perimeter }{ are } \) = \(\frac { 8x }{ 14x² } \) = \(\frac { 9 }{ 7x } \)
Question 3.
The chart shows the average monthly temperatures (in degrees Fahrenheit) and the gas usages (in cubic feet) of a household for 12 months.
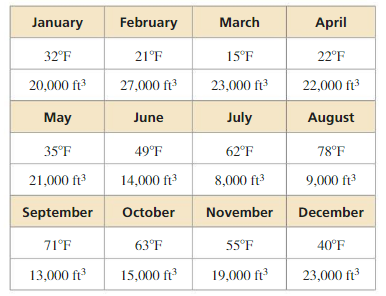
a. Use a graphing calculator to find trigonometric models for the average temperature y1 as a function of time and the gas usage y2 (in thousands of cubic feet) as a function of time. Let t = 1 represent January.
b. Graph the two regression equations in the same coordinate plane on your graphing calculator. Describe the relationship between the graphs.
Answer:
y = 28.5 cos(0.54x + 120.9) + 45.7
y = 7802.9 sin(0.58x + 138.34) + 17323
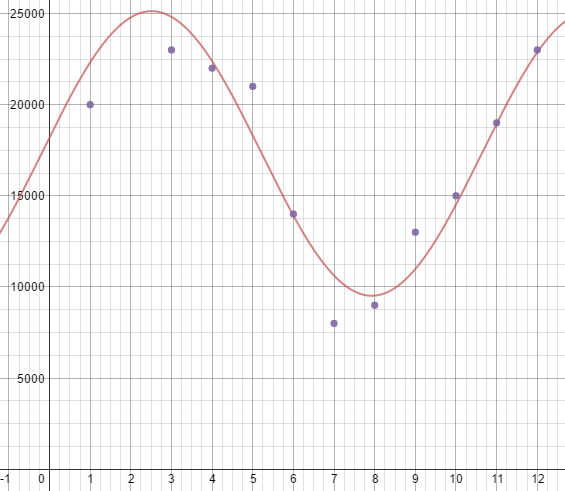
Question 4.
Evaluate each logarithm using log2 5 ≈ 2.322 and log2 3 ≈ 1.585, if necessary. Then order the logarithms by value from least to greatest.
a. log 1000
b. log2 15
c. ln e
d. log2 9
e. log2\(\frac{5}{3}\)
f. log2 1
Answer:
a. 3
b. 3.9
c. 1
d. 0.3
e. 0.7
f. 0
Explanation:
a. log 1000 = log 10³
= 3 log 10
= 3 . 1 = 3
b. log₂ 15 = log₂(3 . 5)
= log₂3 + log₂5
= 3.97
c. loge = 1
d. log₂9 = log₂ 3²
= 2 log₂ 3
= 3.17
e. log₂(5/3) = log₂5 – log₂3
= 0.7
f. log₂1 = 0
Question 5.
Which function is not represented by the graph?
Answer:
A, B, D
Explanation:
A
y = 5sinx
B. y = 5cos(\(\frac { π }{ 2 } \) – x) = 5inx
C. y = 5cos(\(\frac { π }{ 2 } \) + x) = -5sinx
D. y = -5sin(π + x) = 5sinx
Question 6.
Complete each statement with < or > so that each statement is true.
Answer:
a. 0 < 3
b.tanθ < 0
c. θ > 45
Question 7.
Use the Rational Root Theorem and the graph to find all the real zeros of the function f(x) = 2x3 − x2 − 13x− 6. (HSA-APR.B.3)
Answer:
-2, -0.5, 3
Explanation:
Question 8.
Your friend claims −210° is coterminal with the angle \(\frac{5 \pi}{6}\). Is your friend correct? Explain your reasoning.
Answer:
Friend is wrong.
Question 9.
Company A and Company B offer the same starting annual salary of $20,000. Company A gives a $1000 raise each year. Company B gives a 4% raise each year.
a. Write rules giving the salaries an and bn for your nth year of employment at Company A and Company B, respectively. Tell whether the sequence represented by each rule is arithmetic, geometric, or neither.
b. Graph each sequence in the same coordinate plane.
c. Under what conditions would you choose to work for Company B?
d. After 20 years of employment, compare your total earnings.
Answer:
b.