Spike Abacus helps the children who are in primary school to read or write the numbers and to memorize how to do the basic calculations within seconds under any circumstances. As we know the addition and subtraction are basic concepts for children that are taught from Grade 1. For that, students should be aware of all types of digits in numbers.
In numbers, we have 1-digit, 2-digit, 3-digit, and so on. Now, let’s understand the concept of 5-Digits Number on Spike Abacus. Let’s take a look at this article to understand more about 5-digit numbers and how to perform basic operations of five-digit numbers using spike abacus.
Also, Check:
- 1 Digit Number on Spike Abacus
- 2 Digits Number on Spike Abacus
- 3 Digits Number on Spike Abacus
- 4 Digits Number on Spike Abacus
What are 5-Digits Numbers?
Numbers in 5-digits are the numerals that start from 10,000 to 99,999. These numbers include 5-digits in numeric form. The numbers will have their place values to represent them in numerical form. Here, 5-digit numbers themselves have their own place values. These 5-digit numbers contain places as ones, tens, hundreds, thousands, and ten thousands. The given figure shows a representation of a 5-digit number placed by using Spike Abacus.
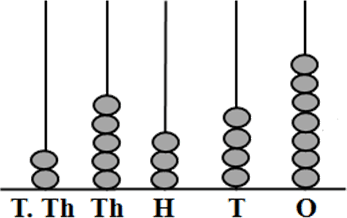
Place Values of 5-Digits Number on Spike Abacus
In 5-digits number every spike is increased by 10 times, where the previous value is multiplied by 10. Let’s take an example to know it practically, the number is 25,234. This number can be written as twenty-five thousand, two hundred thirty-four, where the number 2 in place value of Ten Thousands 2×10000=20,000. Number 5 in the Thousands place 5×1000=5000. Number 2 in Hundreds place 2×100=200. Number 3 in Tens place 3×10=30. Number 4 in One’s place 4×1=4.
Now, add these place values to get the 5-digit number. Therefore, the given 5-digit number can be known as 20,000+5000+200+30+4=25,234. Thus, the representation of five-digit number using Spike Abacus is as below:
Key Points On Five-Digits Numbers
Below key points that help students while solving arithmetic operations on 5-digits numbers using Spike Abacus.
- In a 5-digit number, the smallest number is 10,000 and the greatest number is 99,999.
- 5-Digits numbers are 90,000.
- A 5-digit number should always have 5-digits in it. The digit in Ten Thousand place should never be 0.
Examples on 5-Digits Numbers using Spike Abacus
Example 1:
Show the number 12432 using Spike Abacus.
Solution:
Given number 12,432.
Place the beads in respective place values spikes on the abacus base.
Such as Number 1 in the T-Th place value, keep 1 bead on the T-Th spike. Number 2 in Th place value, keep 2 beads on Th spike. Number 4 in H place value, keep 4 beads in H spike. Number 3 in T place value, keep 3 beads in T spike. Number 2 in O place value, keep 2 beads in O spike.
Now, place all these beads in place value of spikes on the Spike Abacus base. Thus, the representation of a given 5-digit number on Spike Abacus is as below image:
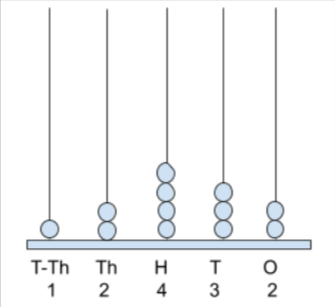
Example 2:
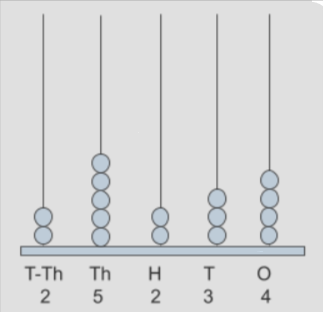
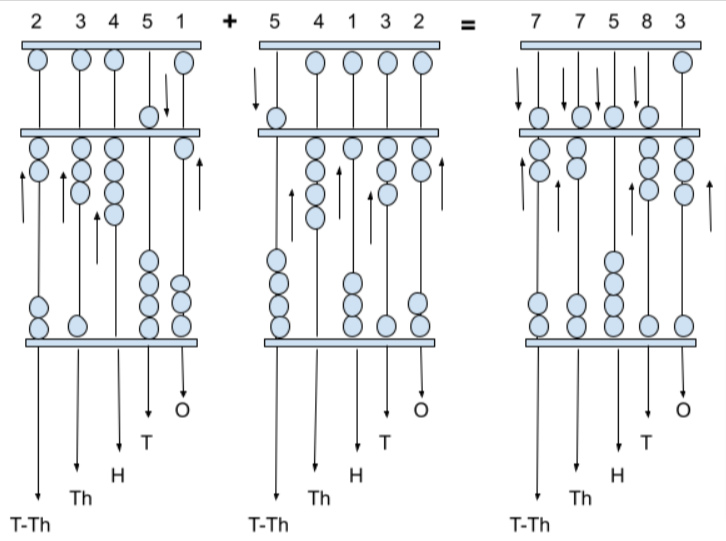
How to do addition for 5-digit numbers 23451, 54132?
Solution:
First, we have to notice the given numbers 23451, 54132.
Now, place the numerals in place values.
23,451- 2 beads in T-Th place, 3 beads in Th place, 4 beads in H place, 5 beads in T place, 1 bead in O place
54,132- 5 beads in T-Th place, 4 beads in Th place, 1 bead in H place, 3 beads in T place, 2 beads in O place.
Next, we have to add these given numbers by moving beads into place values of both spikes. Let us add the given numbers i.e., in ten-thousands place (2+5=7 beads), in thousands place (3+4=7 beads), in the hundreds place (4+1=5 beads), in the tens place (5+3=8 beads), in one’s place (1+2=3 beads).
Thus, the addition of a given number is 77,583.
Let’s represent this addition using spikes on the Abacus base.
Example 3:
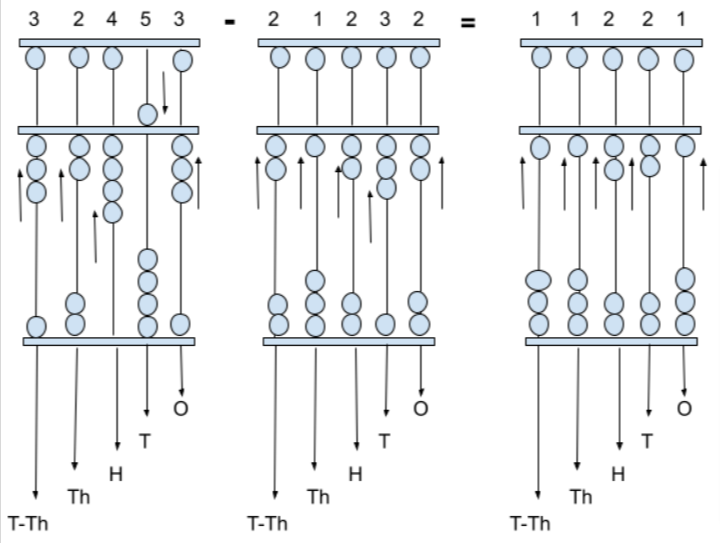
Subtract the 5-digit numbers 32453, 21232.
Solution:
Given numbers are 32453, 21232.
First, notice the place values of digits of given numbers and place the beads on spikes.
32,453- 3 beads in T-Th place, 2 beads in Th place, 4 beads in H place, 5 beads in T place, 3 beads in O place
21,232- 2 beads in T-Th place, 1 bead in Th place, 2 beads in H place, 3 beads in T place, 2 beads in O place.
Now, we have to subtract the numerals or beads by placing them in the Spike Abacus base. Let’s subtract the numbers i.e., in T-Th place (3-2=1 bead), in Th place (2-1=1 bead), in H place (4-2=2 beads), in T place (5-3=2 beads), and in O place (3-2=1 bead). Therefore, the subtraction of numbers given is 11,221.
Let us show this subtraction using spikes on the abacus base.