Engage NY Eureka Math 4th Grade Module 4 End of Module Assessment Answer Key
Eureka Math Grade 4 Module 4 End of Module Assessment Answer Key
Question 1.
Find and draw all lines of symmetry in the following figures. If there are none, write “none.”
a.
Answer:
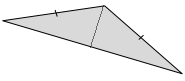
One line of symmetry in the above diagram.
Explanation:
b.
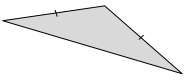
Answer:
There are none.
Explanation:
For the diagram given above, there are no symmetry lines.
c.
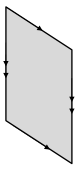
Answer:
There are three lines of symmetry lines.
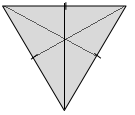
Explanation:
As we know about the line of symmetry from the above diagram we can identify 3 lines of symmetry.
d.
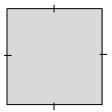
Answer:
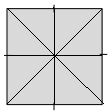
For square, we have 4 lines of symmetrical lines.
Explanation:
By observing the above diagram we can divide the parts into 4 symmetrical lines. Hence square has 4 lines of symmetry.
e.
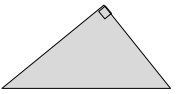
Answer:
There are no symmetrical lines.
Explanation:
By observing the above diagram we know that the object cannot divide into two identical halves. Hence it has no symmetrical lines.
f.

Answer:
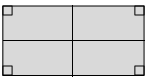
As per the rectangle, we have 2 lines of symmetry.
Explanation:
By applying the rules of symmetry the object can be divided into 2 parts. So by observing the diagram we know that the rectangle has 2 lines of symmetrical lines as it can be folded in half horizontally or vertically.
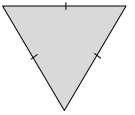
g. For each triangle listed below, state whether it is acute, obtuse, or right and whether it is isosceles, equilateral, or scalene.
Triangle a: _________________________ _________________________
Triangle c: _________________________ _________________________
Triangle e: _________________________ _________________________
Answer:
Triangle a: Obtuse, Isosceles
Traingle c: Acute, Equilateral
Triangle e: Right, Scalene
Explanation:
Triangle a is an obtuse angle that has more than 90° and the triangle is an isosceles triangle, therefore, has both two equal sides and two equal angles.
Triangle c is an acute angle that has less than 90° and here the triangle is an equilateral triangle where all the sides and angles are equal.
Triangle e is right angles triangle i.e is exactly 90° therefore no side is equal to one another.
h. How many lines of symmetry does a circle have? What point do all lines of symmetry for a given circle have in common?

Answer:
As the circle has an infinite amount of lines of symmetry. All lines of symmetry for a circle pass through the center point.
Explanation:
In a circle, each diameter gives an axis of symmetry to the circle. Since an infinite number of diameters can be drawn in a circle; so a circle has infinite lines of symmetry. But, all the symmetries are look-alike, so a circle has only one symmetry of infinite orientations.
Question 2.
In the following figure, QRST is a rectangle. Without using a protractor, determine the measure of ∠RQS Write an equation that could be used to solve the problem.
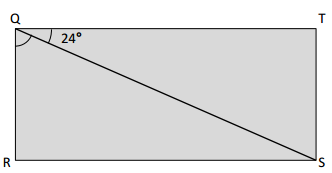
Let us assume ∠Q as W°
The equation that could be solved the problem is
24° + W° = 90°
W° = 90°-24° = 66°
∠RQS = 66°
Explanation:
To determine the ∠RQS we need to write an equation to solve. By observing the diagram we could write the equation as 24° + W° = 90°.
Hence we can determine the value of ∠RQS.
For each part below, explain how the measure of the unknown angle can be found without using a protractor.
a. Find the measure of ∠D.
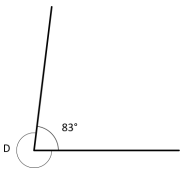
Answer:
To measure the angle we have to subtract 360° from 83° because a circle measures 360°.
so 83°+ ∠D = 360°
∠D=360° – 83°
∠D=277°
Explanation:
A complete trip around the edge of a circle is 360 degrees. So to measure the angle D we need to subtract 360° from 83°. Hence the ∠D=360° – 83°
∠D=277°.
b. In this figure, Q, R, and S lie on a line. Find the measure of ∠QRT
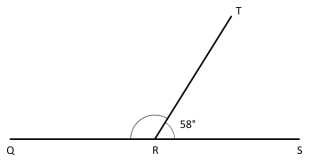
Answer:
To measure the ∠QRT
58°+ ∠QRT = 180°
∠QRT = 180°-58°
∠QRT = 122°
Explanation:
As we know that the line measures 180°, so we need to add 58° with ∠QRT and hence subtract the resultant with 180°.
c. In this figure, Q, R, and S lie on a line, as do P, R, and T. Find the measure of ∠PRS
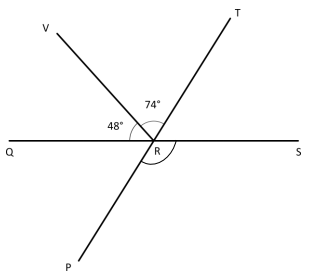
Answer:
First we need to measure ∠TRS
∠VRQ+∠VRT+∠TRS = 180°
48°+74°+∠TRS = 180°
∠TRS = 180°-48°-74°
∠TRS = 180° – 122°
∠TRS = 58°
∠TRS + ∠PRS =180°
58°+ ∠PRS =180°
∠PRS = 180°-58°
∠PRS = 122°
Explanation:
First, to calculate ∠PRS we need to measure ∠TRS. Since Q, R, and S lie on the same line. As we know 48°+74°+∠TRS = 180°. That means we get ∠TRS = 58°.
Also, P, R, and T line on the same line, as we know ∠TRS + ∠PRS = 180°. That means ∠PRS is 122°
Question 3.
Mike drew some two-dimensional figures.
Sketch the figures, and answer each part about the figures that Mike drew.
a. He drew a four-sided figure with four right angles. It is 4 cm long and 3 cm wide.
What type of quadrilateral did Mike draw?
How many lines of symmetry does it have?
Answer:
Mike drew a four-sided figure with four right angles that have 4 cm long and 3 cm wide.
The type of quadrilateral mike drew is a rectangle.
The rectangle has 2 lines of symmetry.
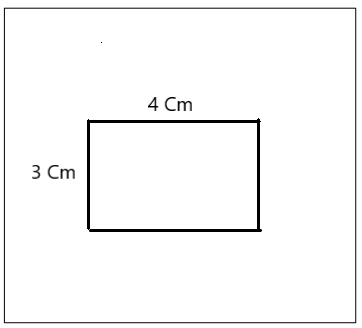
Explanation:
As mentioned in the above question mike drew a four-sided figure with four right angles that have 4 cm long and 3 cm wide. A rectangle has two pairs of opposite sides parallel, and four right angles. So the figure mike drew is a rectangle and it has 2 lines of symmetry.
b. He drew a quadrilateral with four equal sides and no right angles.
What type of quadrilateral did Mike draw?
How many lines of symmetry does it have?
Answer:
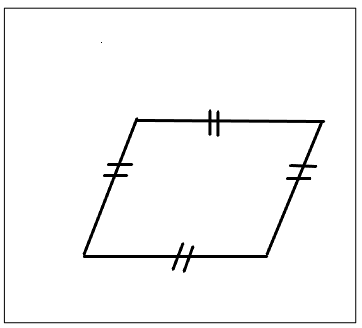
The type of quadrilateral that mike drew is Rhombus.
There are 2 lines of symmetry that the rhombus has.
Explanation:
As the rhombus has four equal-length sides and opposite sides parallel to each other. Hence by observing the diagram we can know that it is a rhombus that has 2 lines of symmetry.
c. He drew a triangle with one right angle and sides that measure 6 cm, 8 cm, and 10 cm.
Classify the type of triangle Mike drew based on side length and angle measure.
How many lines of symmetry does it have?
Answer:
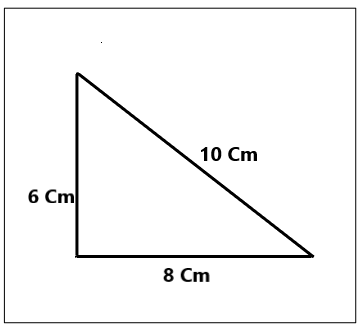
The type of triangle that mike drew is a right-angle triangle. And by observing the dimensions, one can clearly name it as a scalene triangle as all sides have different dimensions.
Explanation:
As the triangle is right angles i.e it has 90°. Hence the triangle mike drew is a right-angled triangle. As the triangle has different dimensions therefore we can name the triangle as a scalene triangle.
d. Using the dimensions given, draw the same shape that Mike drew in Part (c).
Answer:
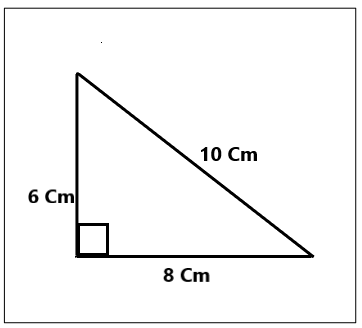
Explanation:
By using the given dimensions mike drew the shape of the right-angled triangle.
e. Mike drew this figure. Without using a protractor, find the sum of ∠FJK, ∠KJH, and ∠HJG.
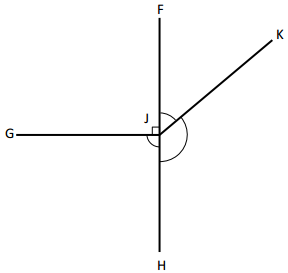
Answer:
360°- 90° = 270°
∠FJK+∠KJH +∠HJG =270°
Explanation:
Here we need to find the sum of ∠FJK, ∠KJH, and ∠HJG. As we already know that the complete trip around the edge of a circle is 360 degrees. Now we need to subtract 360° from 90° to get a sum of other angles. By doing so we get the sum of angles as 270°.
f. Points F, J, and H lie on a line. What is the measure of ∠KJH if ∠FJK measures 45°? Write an equation that could be used to determine the measure of ∠KJH.
Answer:
The equation to measure ∠KJH is
45°+∠KJH =180°
∠KJH = 180°-45°
∠KJH = 135°
Explanation:
We have ∠FJK and points F, J, and H lie on the same line. So to measure ∠KJH we need to write down an equation that is 45°+∠KJH=180°. Hence ∠KJH is 135°.
g.
Mike used a protractor to measure ∠ABC as shown below and said the result was exactly 130° Do you agree or disagree? Explain your thinking.
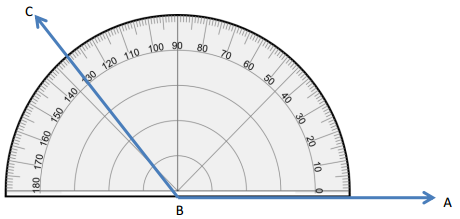
Answer:
I disagree. Because mike didn’t use the protractor properly. The 0° should match up with BA but it doesn’t match up.
Explanation:
We can completely disagree with mike’s statement because he doesn’t measure the exact result as he didn’t use the protractor properly. In the diagram, mike lined up the bottom of the protractor with BA instead.
h. Below is half of a line-symmetric figure and its line of symmetry. Use a ruler to complete Mike’s drawing.
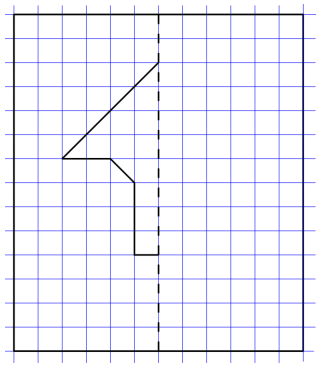
Answer:
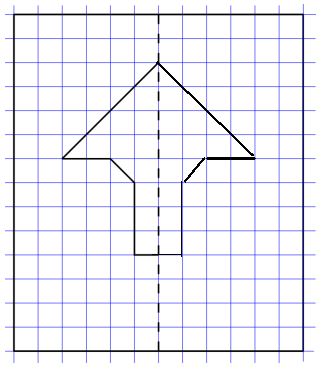
Explanation:
As mentioned in the question we have completed mike’s half of a line-symmetric figure and its line of symmetry using the ruler.