Eureka Math Grade 3 Module 7 – Eureka Math Answers

Eureka Math Grade 3 Module 7 Lesson 19 Answer Key

August 12, 2021

Engage NY Eureka Math 3rd Grade Module 7 Lesson 19 Answer Key

Eureka Math Grade 3 Module 7 Lesson 19 Problem Set Answer Key

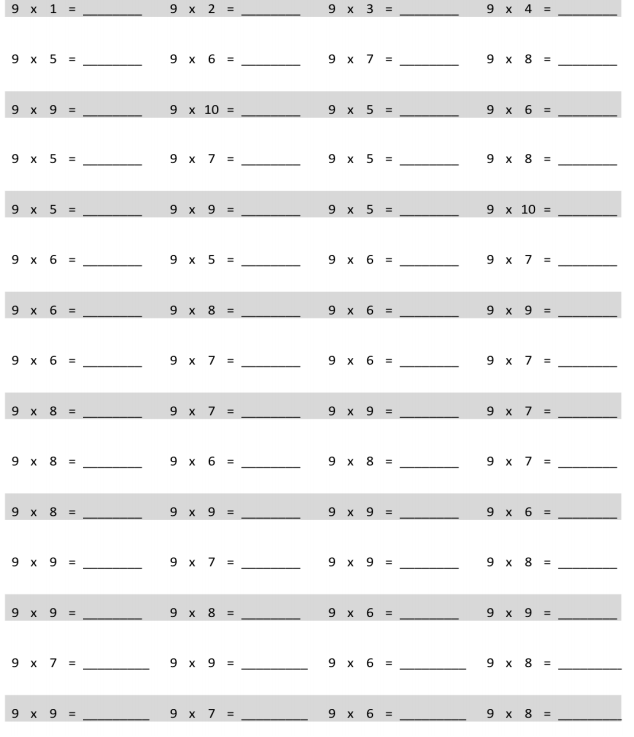
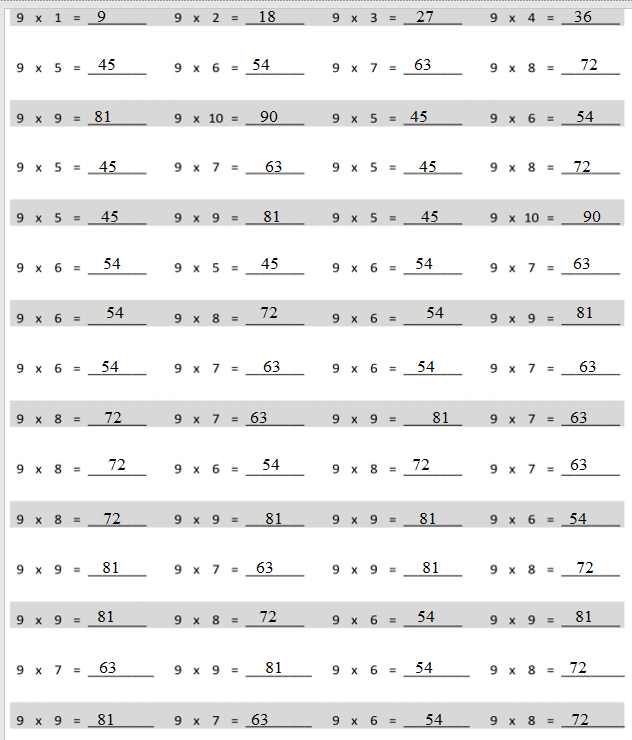
Question 1.
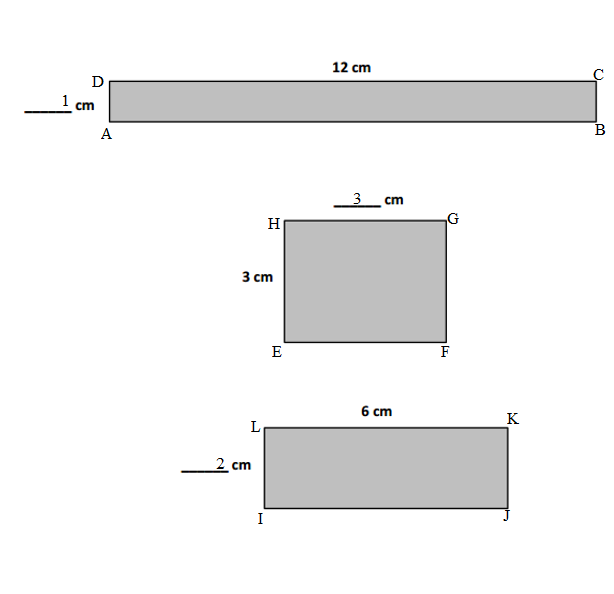
Use unit square tiles to make rectangles for each given number of unit squares. Complete the charts to show how many rectangles you can make for each given number of unit squares. The first one is done for you. You might not use all the spaces in each chart.

Number of unit squares = 12 Number of rectangles I made: 3
Width	Length
1	12
2	6
3	4

Answer:

Number of unit squares = 13 Number of rectangles I made: _________
Width	Length
1	13

Number of unit squares = 13 Number of rectangles I made: ____1_____
Width	Length
1	13

Number of unit squares = 14 Number of rectangles I made: __2_______
Width	Length
1	14
2	7

Number of unit squares = 15 Number of rectangles I made: _____2____
Width	Length
1	15
2	6

Number of unit squares = 16 Number of rectangles I made: ___3______
Width	Length
1	16
4	5
2	6

Number of unit squares = 17 Number of rectangles I made: _____2____
Width	Length
1	17
2	7

Number of unit squares = 18 Number of rectangles I made: __3______
Width	Length
1	18
3	6
2	9

Explanation:
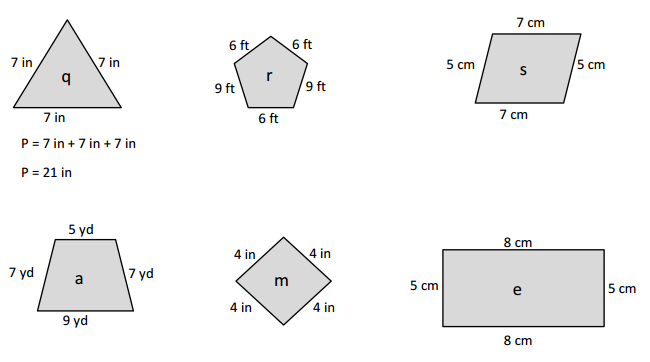
Perimeter of rectangle = 2 ( Length + Width )

Question 2.
Create a line plot with the data you collected in Problem 1.
Number of Rectangles Made with Unit Squares
$Engage NY Math Grade 3 Module 7 Lesson 19 Problem Set Answer Key pr 1$
Answer:
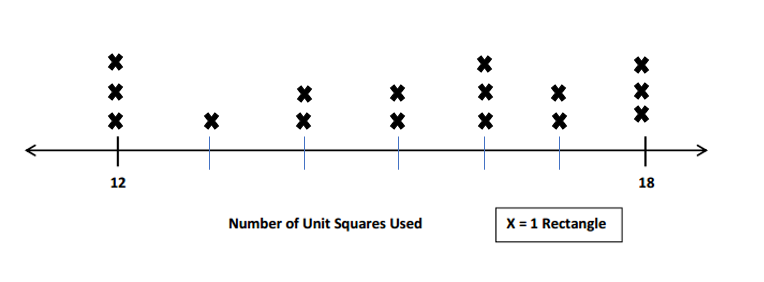
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-19-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 19 Problem Set Answer Key-2$
Explanation:
Number of Rectangles Made with Unit Squares in the Problem 1 are plotted using the number line as X = 1 Rectangle on each number.

Question 3.
Which numbers of unit squares produce three rectangles?
Answer:
The numbers of unit squares produce three rectangles are number 12, number 16 and the number 18.

Explanation:
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-19-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 19 Problem Set Answer Key-2$
The numbers of unit squares produce three rectangles are number 12, number 16 and the number 18.

Question 4.
Why do some numbers of unit squares, such as 13, only produce one rectangle?
Answer:
Some numbers likely to produce only one rectangle because they have only one pair of factors that can multiply to make that number. So, among that numbers 13 is one of the numbers.

Explanation:
Some numbers likely to produce only one and itself. They have only one pair of factors that can multiply to make that number. So, among that numbers 13 is one of the numbers.

Eureka Math Grade 3 Module 7 Lesson 19 Exit Ticket Answer Key

Use unit square tiles to make rectangles for the given number of unit squares. Complete the chart to show how many rectangles you made for the given number of unit squares. You might not use all the spaces in the chart.

Number of unit squares = 20 Number of rectangles I made: _____4____
Width	Length

Answer:
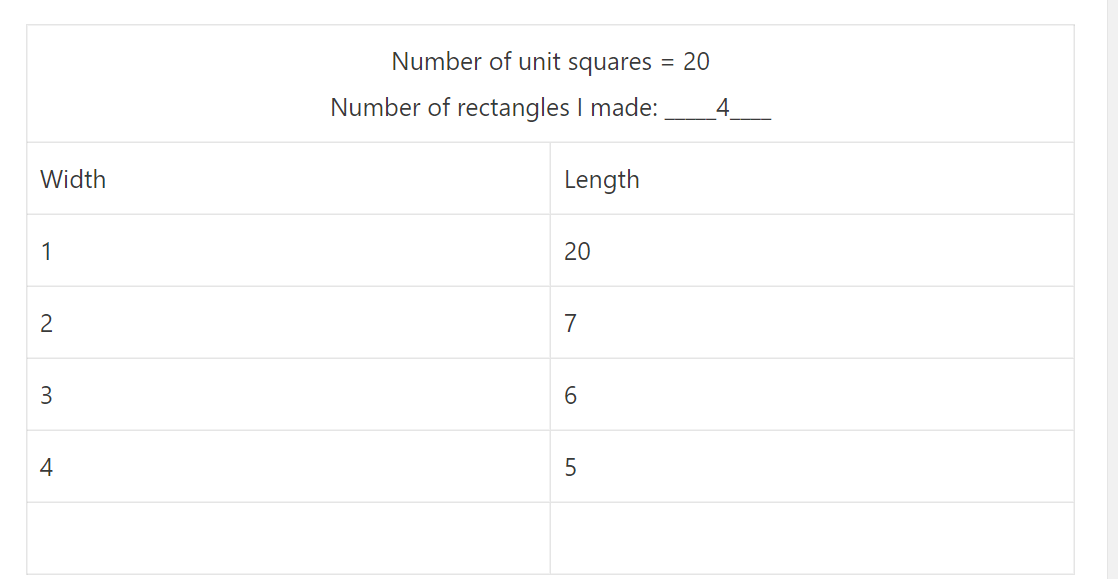
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-19-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 19 Exit Ticket Answer Key$

Explanation:
Number of rectangles formed by using 20 square tiles = 4.

Eureka Math Grade 3 Module 7 Lesson 19 Homework Answer Key

Question 1.
Cut out the unit squares at the bottom of the page. Then, use them to make rectangles for each given number of unit squares. Complete the charts to show how many rectangles you can make for each given number of unit squares. You might not use all the spaces in each chart.

Answer:

Number of unit squares = 6 Number of rectangles I made: ____2___
Width	Length
1	6
2	3

Number of unit squares = 7 Number of rectangles I made: ____1_____
Width	Length
1	7

Number of unit squares = 8 Number of rectangles I made: _________
Width	Length
1	8
2	6

Number of unit squares = 9 Number of rectangles I made: _________
Width	Length
1	9
3	3

Number of unit squares = 10 Number of rectangles I made: _________
Width	Length
1	10
2	5

Number of unit squares = 11 Number of rectangles I made: _________
Width	Length
1	11

$Eureka Math Grade 3 Module 7 Lesson 19 Homework Answer Key h 1$
Answer:
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-19-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 19 Exit Ticket Answer Key-1$ Explanation:
Number of rectangles formed by using given number of square tiles are counted and represented in the table chart.

Question 2.
Create a line plot with the data you collected in Problem 1.
Number of Rectangles Made with Unit Squares
$Eureka Math Grade 3 Module 7 Lesson 19 Homework Answer Key h 2$
a. Luke looks at the line plot and says that all odd numbers of unit squares produce only 1 rectangle. Do you agree? Why or why not?
b. How many X’s would you plot for 4 unit squares? Explain how you know.

Answer:
a. Luke looks at the line plot and says that all odd numbers of unit squares produce only 1 rectangle. No, I disagree with the Luke’s statement because only prime numbers have factors as itself and number one. Here, numbers 7 and 11 are prime numbers not odd numbers, so they have only formed one rectangle.

b. Number of rectangles formed by 4 unit square are only 2 because number 4 has factors as 1 and itself and number 2.

Explanation:
a. $Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-19-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 19 Exit Ticket Answer Key-2a$
Prime numbers are the positive integers having only two factors, 1 and the integer itself.
Odd numbers are whole numbers that cannot be divided exactly into pairs.

b. Factors of number 4 =( 1, 4 ); ( 2,2 ).
Number of rectangles formed by 4 unit square are only 2 because number 4 has factors as 1 and itself and number 2.

Eureka Math Grade 3 Module 7 Lesson 18 Answer Key

August 12, 2021

Engage NY Eureka Math 3rd Grade Module 7 Lesson 18 Answer Key

Eureka Math Grade 3 Module 7 Lesson 18 Problem Set Answer Key

Question 1.
Use unit squares to build as many rectangles as you can with an area of 24 square units. Shade in squares on your grid paper to represent each rectangle that you made with an area of 24 square units.
a. Estimate to draw and label the side lengths of each rectangle you built in Problem 1. Then, find the perimeter of each rectangle. One rectangle is done for you.
$Engage NY Math Grade 3 Module 7 Lesson 18 Problem Set Answer Key pr 1$
P = 24 units + 1 unit + 24 units + 1 unit = 50 units
b. The areas of the rectangles in part (a) above are all the same. What do you notice about the perimeters?
Answer:
a. Perimeter of ABCD rectangle = 22units.
Perimeter of EFGH rectangle = 28units.
Perimeter of IJKL rectangle = 20units.

b. All rectangles drawn in the above1.a are not the same sided figures. They are not having same perimeters because their lengths are different compared to one another.

Explanation:
a.
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-18-Answer-Key-Eureka Math 3rd Grade Module 7 Lesson 18-1a$
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-18-Answer-Key-Eureka Math 3rd Grade Module 7 Lesson 18-1a..$
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-18-Answer-Key-Eureka Math 3rd Grade Module 7 Lesson 18-1a....$
Perimeter of ABCD rectangle = Side + Side + Side + Side
= AB + BC + CD + DA
= 8units + 3units + 8units + 3units
= 11units + 8units + 3units
= 19units + 3units
= 22units.
Perimeter of EFGH rectangle = Side + Side + Side + Side
= EF + FG + GH + HE
= 12units + 2units + 12units + 2units
= 14units + 12units + 2units
= 26units + 2units
= 28units.
Perimeter of IJKL rectangle = Side + Side + Side + Side
= IJ + JK + KL + KI
= 6units + 4 units + 6units + 4 units
= 10units + 6units + 4units
= 16units + 4units
= 20units.

b. All rectangles drawn in the above 1a are not the same figures. They are not having same perimeters.

Question 2.
Use unit square tiles to build as many rectangles as you can with an area of 16 square units. Estimate to draw each rectangle below. Label the side lengths.
a. Find the perimeters of the rectangles you built.
b. What is the perimeter of the square? Explain how you found your answer.
Answer:
a. Perimeter of OPQR Rectangle = 14units.
Perimeter of EFGH Rectangle = 34units.

b. Perimeter of ABCD Square= 16units. As, the sides in a square are equal, we can multiple the number of sides into the side value to get the Perimeter of square instead of adding them separately.

Explanation:
a.
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-18-Answer-Key-Eureka Math 3rd Grade Module 7 Lesson 18-2a..$
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-18-Answer-Key-Eureka Math 3rd Grade Module 7 Lesson 18-2a....$
Perimeter of OPQR Rectangle = Side + Side + Side + Side
= OP + PQ + QR + RO
= 5units + 2units + 5units + 2units
= 7units + 5units + 2units
= 12units + 2units
= 14units.
Perimeter of EFGH Rectangle = Side + Side + Side + Side
= EF + FG+ GH + HE
= 16units + 1unit + 16units + 1unit
= 17units + 16units + 1unit
= 33units + 1unit
= 34unit.

b.
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-18-Answer-Key-Eureka Math 3rd Grade Module 7 Lesson 18-2a$
Perimeter of ABCD Square= 4 × Side
= 4 × 4units
= 16units.

Question 3.
Doug uses square unit tiles to build rectangles with an area of 15 square units. He draws the rectangles as shown below but forgets to label the side lengths. Doug says that Rectangle A has a greater perimeter than Rectangle B. Do you agree? Why or why not?
$Engage NY Math Grade 3 Module 7 Lesson 18 Problem Set Answer Key pr 2$
Answer:
Yes, Doug is correct, the perimeter of rectangle A is greater than the perimeter of the rectangle B because in the appearance itself we notice that rectangle A is bigger in size than that of rectangle B.

Explanation:
$Engage NY Math Grade 3 Module 7 Lesson 18 Problem Set Answer Key pr 2$
Well, comparing the rectangles drawn by Doug its easy to say rectangle A is going to have the greater perimeter that compared to the perimeter of the rectangle B because the size of the rectangle A is bigger than that of rectangle B.

Eureka Math Grade 3 Module 7 Lesson 18 Exit Ticket Answer Key

Tessa uses square-centimeter tiles to build rectangles with an area of 12 square centimeters. She draws the rectangles as shown below. Label the unknown side lengths of each rectangle. Then, find the perimeter of each rectangle.
$Eureka Math 3rd Grade Module 7 Lesson 18 Exit Ticket Answer Key t 1$
P = _____
$Eureka Math 3rd Grade Module 7 Lesson 18 Exit Ticket Answer Key t 2$
P = _____
$Eureka Math 3rd Grade Module 7 Lesson 18 Exit Ticket Answer Key t 3$
P = _____
Answer:
Perimeter of the ABCD Rectangle = 26cm.
Perimeter of the EFGH Rectangle = 12cm.
Perimeter of the IJKL Rectangle = 16cm.

Explanation:
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-18-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 18 Exit Ticket Answer Key$
The unknown side are measured by using a ruler by me.
Perimeter of the ABCD Rectangle = Side + Side + Side + Side
= AB + BC + CD + DA
= 12cm + 1cm + 12cm + 1cm
= 13cm + 12cm + 1cm
= 25cm + 1cm
= 26cm.
Perimeter of the EFGH Rectangle = Side + Side + Side + Side
= EF + FG + GH+ HE
= 3cm + 3cm + 3cm + 3cm
= 6cm + 3cm + 3cm
= 9cm + 3cm
= 12cm.
Perimeter of the IJKL Rectangle = Side + Side + Side + Side
IJ + JK + KL + KI
= 6cm + 2cm + 6cm + 2cm
= 8cm + 6cm + 2cm
= 14cm + 2cm
= 16cm.

Eureka Math Grade 3 Module 7 Lesson 18 Homework Answer Key

Question 1.
Shade in squares on the grid below to create as many rectangles as you can with an area of 18 square centimeters.
$Eureka Math Grade 3 Module 7 Lesson 18 Homework Answer Key h 1$
Answer:
ABCD rectangle
EFGH rectangle
IJKL rectangle.

Explanation:
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-18-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 18 Homework Answer Key$

Question 2.
Find the perimeter of each rectangle in Problem 1 above.
Answer:
Perimeter of the ABCD rectangle = 20units.
Perimeter of the EFGH rectangle = 12units.
Perimeter of the IJKL rectangle = 18units.

Explanation:
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-18-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 18 Homework Answer Key$

Perimeter of the ABCD rectangle = Side + Side + Side + Side
= AB + BC + CD + DA
= 8units + 2units + 8units + 2units
= 10units + 8units + 2units
= 18units + 2units
= 20units.
Perimeter of the EFGH rectangle = Side + Side + Side + Side
= EF + FG + GH+ HE
= 4units + 2units + 4units + 2units
= 6units + 4units + 2units
= 10units + 2units
= 12units.
Perimeter of the IJKL rectangle = Side + Side + Side + Side
= IJ + JK + KL + LI
= 5units + 4units + 5units + 4units
= 9units + 5units + 4units
= 14units + 4units
= 18units.

Question 3.
Estimate to draw as many rectangles as you can with an area of 20 square centimeters. Label the side lengths of each rectangle.
a. Which rectangle above has the greatest perimeter? How do you know just by looking at its shape?
b. Which rectangle above has the smallest perimeter? How do you know just by looking at its shape?
Answer:
a. Among all the three rectangles drawn, through looks IJKL Rectangles is having greater perimeter compared to other rectangles. We can say that by seeing the length of the rectangles, which length is high that going to have greater perimeter.

b. Among all the three rectangles drawn, through looks EFGH Rectangles is having smallest perimeter compared to other rectangles. We can say that by seeing the length of the rectangles.

Explanation:
a.
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-18-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 18 Homework Answer Key-3$

Perimeter of the ABCD Rectangle = Side + Side + Side + Side
= AB + BC + CD + DA
= 7units + 4units + 7units + 4units
= 11units + 7units + 4units
= 18units + 4units
= 22units.
Perimeter of the EFGH Rectangle = Side + Side + Side + Side
= EF + FG + GH + HE
= 5units + 3units + 5units + 3units
= 8units + 5units + 3units
= 13units + 3units
= 16units.
Perimeter of the IJKL Rectangle = Side + Side + Side + Side
= IJ + JK + KL + LI
= 11units + 2units + 11units + 2units
= 13units + 11units + 2units
= 24units + 2units
= 26 units.

b. Among all the three rectangles drawn, through looks EFGH Rectangles is having the smallest perimeter compared to other rectangles. We can say that by seeing the length of the rectangles, which length is small that going to have the smallest perimeter.

Eureka Math Grade 3 Module 7 Mid Module Assessment Answer Key

August 12, 2021

Engage NY Eureka Math 3rd Grade Module 7 Mid Module Assessment Answer Key

Eureka Math Grade 3 Module 7 Mid Module Assessment Task Answer Key

Question 1.
Three shapes are shown below.
a. Circle the shape(s) with only one pair of parallel sides.
b. Cross out the shape(s) with two pairs of parallel sides.
$Engage NY Math 3rd Grade Module 7 Mid Module Assessment Answer Key 1$
c. Which of the three shapes are quadrilaterals? Explain how you know.
Answer:

Question 2.
Use your ruler and right angle tool to draw the following shapes.
a. Draw and name a shape with four right angles.
b. Draw a four-sided shape with no right angles and no equal sides. Label the side lengths.
c. Draw triangles to create a rhombus. Label the side lengths.
Answer:

Question 3.
Mr. Cooper builds a fence to make a rectangular horse stall. The stall is 5 meters long and 7 meters wide. How many meters of fence does Mr. Cooper use? Draw a picture and write an equation to show your thinking.
Answer:

Question 4.
Jamal wants to put wood trim around his rectangular bedroom and square closet. His bedroom is 10 feet wide and 8 feet long. His closet is 3 feet wide and 3 feet long.
$Engage NY Math 3rd Grade Module 7 Mid Module Assessment Answer Key 2$
a. Wood trim is sold by the foot. How many feet of wood trim does Jamal need to go around his bedroom and closet? Show your work.
b. How much more wood trim does Jamal need for his bedroom than his closet? Write and solve an equation. Use a letter to represent the unknown.
Answer:

Question 5.
The figure below is composed of rectangles. Use the picture and the descriptions to find the perimeter of the shape. Show your work.
Each side labeled with A is 6 inches.
Each side labeled with B is 3 inches.
Each side labeled with C is 8 inches.
$Engage NY Math 3rd Grade Module 7 Mid Module Assessment Answer Key 3$
Answer:

Question 6.
Mrs. Gomez builds a fence around her backyard. Her plan shows the fence as a dotted line below.
$Engage NY Math 3rd Grade Module 7 Mid Module Assessment Answer Key 4$
Together, the garage and backyard make a rectangle. The fence goes only where there is a dotted line. How many feet of fence does Mrs. Gomez need to build? Show your work.
Answer:

Eureka Math Grade 3 Module 7 Lesson 17 Answer Key

August 12, 2021

Engage NY Eureka Math 3rd Grade Module 7 Lesson 17 Answer Key

Eureka Math Grade 3 Module 7 Lesson 17 Problem Set Answer Key

Question 1.
The shapes below are made up of rectangles. Label the unknown side lengths. Then, write and solve an equation to find the perimeter of each shape.
a.
$Engage NY Math Grade 3 Module 7 Lesson 17 Problem Set Answer Key pr 1$
P =
Answer:
Perimeter of the given figure = 16 cm.

Explanation:
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-17-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 17 Problem Set Answer Key-1a$
Length of the side AB in the given figure = 4 cm
Length of the side BC in the given figure = 2 cm
Length of the side CD in the given figure = 2 cm
Length of the side ED in the given figure = 1 cm
Length of the side EF in the given figure = 2 cm
Length of the side FA in the given figure = 3 cm
Length of the side GD in the given figure = 2 cm
Perimeter of the given figure = Length of the side AB + Length of the side BC + Length of the side CD + Length of the side ED + Length of the side EF + Length of the side FA + Length of the side GD
= 4 cm + 2 cm + 2 cm + 1 cm + 2 cm + 3 cm + 2cm
= 6 cm + 2 cm + 1 cm + 2 cm + 3 cm + 2cm
= 8 cm + 1 cm + 2 cm + 3 cm + 2cm
= 9 cm + 2 cm + 3 cm + 2cm
= 11 cm + 3 cm + 2cm
= 14 cm + 2 cm
= 16 cm.

b.
$Engage NY Math Grade 3 Module 7 Lesson 17 Problem Set Answer Key pr 2$
P =
Answer:
Perimeter of the given figure = 16ft.

Explanation:
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-17-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 17 Problem Set Answer Key-1b$
Length of the side AB in the given figure = 2ft
Length of the side BC in the given figure = 1ft
Length of the side CD in the given figure = 1ft
Length of the side DE in the given figure = 1ft
Length of the side EF in the given figure = 2ft
Length of the side GF in the given figure = 2ft
Length of the side GH in the given figure = 5ft
Length of the side HA in the given figure = 2ft
Perimeter of the given figure = Length of the side AB + Length of the side BC + Length of the side CD + Length of the side DE + Length of the side EF + Length of the side GF + Length of the side GH + Length of the side HA
= 2ft + 1ft + 1ft + 1ft + 2ft + 2ft+ 5ft + 2ft
= 3ft + 1ft + 1ft + 2ft + 2ft+ 5ft + 2ft
= 4ft + 1ft + 2ft + 2ft+ 5ft + 2ft
= 5ft + 2ft + 2ft+ 5ft + 2ft
= 7ft + 2ft + 5ft + 2ft
= 9ft + 5ft + 2ft
= 14ft + 2ft
= 16ft.

c.
$Engage NY Math Grade 3 Module 7 Lesson 17 Problem Set Answer Key pr 3$
P =
Answer:
Perimeter of the given figure = 24m.

Explanation:
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-17-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 17 Problem Set Answer Key-1c$
Length of the side AB in the given figure = 2m
Length of the side BC in the given figure = 2m
Length of the side CD in the given figure = 4m
Length of the side DE in the given figure = 2m
Length of the side EF in the given figure = 4m
Length of the side GF in the given figure = 2m
Length of the side GH in the given figure = 2m
Length of the side HA in the given figure = 6m
Perimeter of the given figure = Length of the side AB + Length of the side BC + Length of the side CD + Length of the side DE + Length of the side EF + Length of the side GF + Length of the side GH + Length of the side HA
= 2m + 2m + 4m + 2m + 4m + 2m + 2m + 6m
= 4m + 4m + 2m + 4m + 2m + 2m + 6m
= 8m + 2m + 4m + 2m + 2m + 6m
= 10m + 4m + 2m + 2m + 6m
= 14m + 2m + 2m + 6m
= 16m + 2m + 6m
= 18m + 6m
= 24m.

d.
$Engage NY Math Grade 3 Module 7 Lesson 17 Problem Set Answer Key pr 4$
P =
Answer:
Perimeter of the given figure = 26yd.

Explanation:
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-17-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 17 Problem Set Answer Key-1d$
Length of the side AB in the given figure = 7yd
Length of the side BC in the given figure = 2yd
Length of the side CD in the given figure = 2yd
Length of the side DE in the given figure = 4yd
Length of the side EF in the given figure = 2yd
Length of the side FG in the given figure = 2yd
Length of the side GH in the given figure = 1yd
Length of the side HI in the given figure = 2yd
Length of the side IJ in the given figure = 2yd
Length of the side JA in the given figure = 2yd
Perimeter of the given figure = Length of the side AB + Length of the side BC + Length of the side CD + Length of the side DE + Length of the side EF + Length of the side FG + Length of the side GH + Length of the side HI + Length of the side IJ + Length of the side JA
= 7yd + 2yd + 2yd + 4yd + 2yd + 2yd + 1yd + 2yd + 2yd + 2yd
= 9yd + 2yd + 4yd + 2yd + 2yd + 1yd + 2yd + 2yd + 2yd
= 11yd + 4yd + 2yd + 2yd + 1yd + 2yd + 2yd + 2yd
= 15yd + 2yd + 2yd + 1yd + 2yd + 2yd + 2yd
= 17yd + 2yd + 1yd + 2yd + 2yd + 2yd
= 19yd + 1yd + 2yd + 2yd + 2yd
= 20yd + 2yd + 2yd + 2yd
= 22yd + 2yd + 2yd
= 24yd + 2yd
= 26yd.

Question 2.
Nathan draws and labels the square and rectangle below. Find the perimeter of the new shape.
$Engage NY Math Grade 3 Module 7 Lesson 17 Problem Set Answer Key pr 5$
Answer:
Perimeter of the ACDF new shape = 48cm.

Explanation:
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-17-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 17 Problem Set Answer Key-2$
Length of the side of AB in the given figure = 6cm
Length of the side of BC in the given figure = 12cm
Length of the side of CD in the given figure = 6cm
Length of the side of DE in the given figure = 12cm
Length of the side of EF in the given figure = 6cm
Length of the side of FA in the given figure = 6cm
Perimeter of the ACDF new shape = Length of the side of AB + Length of the side of BC + Length of the side of CD + Length of the side of DE + Length of the side of EF + Length of the side of FA
= 6cm + 12cm + 6cm + 12cm + 6cm + 6cm
= 18cm + 6cm + 12cm + 6cm + 6cm
= 24cm + 12cm + 6cm + 6cm
= 36cm + 6cm + 6cm
= 42cm + 6cm
= 48cm.

Question 3.
Label the unknown side lengths. Then, find the perimeter of the shaded rectangle.
$Engage NY Math Grade 3 Module 7 Lesson 17 Problem Set Answer Key pr 6$
Answer:
Perimeter of the DFGC shaded rectangle = 26in.

Explanation:
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-17-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 17 Problem Set Answer Key-3$
Shaded rectangle = DFGC
Length of the side of AB of the given figure = 16in
Length of the side of BG of the given figure = 2in
Length of the side of GC of the given figure = EA – BG = 7in – 2in = 5in.
Length of the side of CD of the given figure= AB – DE = 16in – 8in = 8in.
Length of the side of DE of the given figure= 8in
Length of the side of EA of the given figure= 7in
Length of the side of DF of the given figure= 5in
Length of the side of FG of the given figure= 8in
Perimeter of the DFGC shaded rectangle = Length of the side of FG + Length of the side of GC + Length of the side of CD + Length of the side of DF
= 8in + 5in + 8in + 5in
= 13in + 8in + 5in
= 21in + 5in
= 26in.

Eureka Math 3rd Grade Module 7 Lesson 17 Exit Ticket Answer Key

Label the unknown side lengths. Then, find the perimeter of the shaded rectangle.
$Eureka Math 3rd Grade Module 7 Lesson 17 Exit Ticket Answer Key t 1$
Answer:
Perimeter of the FGDE shaded rectangle = 30m.

Explanation:
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-17-Answer-Key-Eureka Math 3rd Grade Module 7 Lesson 17 Exit Ticket Answer Key$
Shaded rectangle = FGDE
Length of the side AB in the given figure = 12m
Length of the side BC in the given figure = 14m
Length of the side CD in the given figure = 5m
Length of the side DE in the given figure = AB – CD = 12m – 5m = 7m.
Length of the side EF in the given figure = BC – FA = 14m – 6m = 8m.
Length of the side FA in the given figure = 6m
Length of the side FG in the given figure = 7m
Length of the side GD in the given figure = 8m
Perimeter of the FGDE shaded rectangle = Length of the side FG + Length of the side GD + Length of the side DE + Length of the side EF
= 7m + 8m + 7m + 8m
= 15m + 7m + 8m
= 22m + 8m
= 30m.

Eureka Math Grade 3 Module 7 Lesson 17 Homework Answer Key

Question 1.
The shapes below are made up of rectangles. Label the unknown side lengths. Then, write and solve an equation to find the perimeter of each shape.
a.
$Eureka Math Grade 3 Module 7 Lesson 17 Homework Answer Key h 1$
P =
Answer:
Perimeter of the given figure = 32m.

Explanation:
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-17-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 17 Homework Answer Key-1$
Length of the side of AB in the given figure = 4m
Length of the side of BC in the given figure = 9m
Length of the side of CD in the given figure = 7m
Length of the side of DE in the given figure = 2m
Length of the side of EF in the given figure = 3m
Length of the side of FA in the given figure = 7m
Perimeter of the given figure = Length of the side of AB + Length of the side of BC + Length of the side of CD + Length of the side of DE + Length of the side of EF + Length of the side of FA
= 4m + 9m + 7m + 2m + 3m + 7m
= 13m + 7m + 2m + 3m + 7m
= 20m + 2m + 3m + 7m
= 22m + 3m + 7m
= 25m + 7m
= 32m.

b.
$Eureka Math Grade 3 Module 7 Lesson 17 Homework Answer Key h 2$
P =
Answer:
Perimeter of the given figure = 34 cm.

Explanation:
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-17-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 17 Homework Answer Key-2$

Length of the side of AB in the given figure = 2 cm
Length of the side of BC in the given figure = 4 cm
Length of the side of CD in the given figure = 4 cm
Length of the side of DE in the given figure = 3 cm
Length of the side of EF in the given figure = 2 cm
Length of the side of FG in the given figure = 5 cm
Length of the side of GH in the given figure = 8 cm
Length of the side of HA in the given figure = 6 cm
Perimeter of the given figure = Length of the side of AB + Length of the side of BC + Length of the side of CD + Length of the side of DE + Length of the side of EF + Length of the side of FG + Length of the side of GH + Length of the side of HA
= 2 cm + 4 cm + 4 cm + 3 cm + 2 cm + 5 cm + 8 cm + 6 cm
= 6 cm + 4 cm + 3 cm + 2 cm + 5 cm + 8 cm + 6 cm
= 10 cm + 3 cm + 2 cm + 5 cm + 8 cm + 6 cm
= 13 cm + 2 cm + 5 cm + 8 cm + 6 cm
= 15 cm + 5 cm + 8 cm + 6 cm
= 20 cm + 8 cm + 6 cm
= 28 cm + 6 cm
= 34 cm.

c.
$Eureka Math Grade 3 Module 7 Lesson 17 Homework Answer Key h 3$
P =
Answer:
Perimeter of the given figure = 40in.

Explanation:
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-17-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 17 Homework Answer Key-1c$
Length of the side of AB in the given figure = 12in
Length of the side of BC in the given figure = 2in
Length of the side of CD in the given figure = 4in
Length of the side of DE in the given figure = 6in
Length of the side of EF in the given figure = 4in
Length of the side of FG in the given figure = 6in
Length of the side of GH in the given figure = 4in
Length of the side of HA in the given figure = 2in
Perimeter of the given figure = Length of the side of AB + Length of the side of BC + Length of the side of CD + Length of the side of DE + Length of the side of EF + Length of the side of FG + Length of the side of GH + Length of the side of HA
= 12in + 2in + 4in + 6in + 4in + 6in + 4in + 2in
= 14in + 4in + 6in + 4in + 6in + 4in + 2in
= 18in + 6in + 4in + 6in + 4in + 2in
= 24in + 4in + 6in + 4in + 2in
= 28in + 6in + 4in + 2in
= 34in + 4in + 2in
= 38in + 2in
= 40in.

d.
$Eureka Math Grade 3 Module 7 Lesson 17 Homework Answer Key h 4$
P =
Answer:
Perimeter of the given figure = 30ft.

Explanation:
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-17-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 17 Homework Answer Key-1d$

Length of the side of AB in the given figure = 8ft
Length of the side of BC in the given figure = 3ft
Length of the side of CD in the given figure = 3ft
Length of the side of DE in the given figure = 1ft
Length of the side of EF in the given figure = 3ft
Length of the side of FG in the given figure = 3ft
Length of the side of GH in the given figure = 2ft
Length of the side of HA in the given figure = 7ft
Perimeter of the given figure = Length of the side of AB + Length of the side of BC + Length of the side of CD + Length of the side of DE + Length of the side of EF + Length of the side of FG + Length of the side of GH + Length of the side of HA
= 8ft + 3ft + 3ft + 1ft + 3ft + 3ft + 2ft + 7ft
= 11ft + 3ft + 1ft + 3ft + 3ft + 2ft + 7ft
= 14ft + 1ft + 3ft + 3ft + 2ft + 7ft
= 15ft + 3ft + 3ft + 2ft + 7ft
= 18ft + 3ft + 2ft + 7ft
= 21ft + 2ft + 7ft
= 23ft + 7ft
= 30ft.

Question 2.
Sari draws and labels the squares and rectangle below. Find the perimeter of the new shape.
$Eureka Math Grade 3 Module 7 Lesson 17 Homework Answer Key h 5$
Answer:
Perimeter of the new shape = 72cm.

Explanation:
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-17-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 17 Homework Answer Key-2..$

Length of the side of AB in the given figure = 6cm
Length of the side of BC in the given figure = 18cm
Length of the side of CD in the given figure = 6cm
Length of the side of DE in the given figure = 6cm
Length of the side of EF in the given figure = 6cm
Length of the side of FG in the given figure = 18cm
Length of the side of GH in the given figure = 6cm
Length of the side of HA in the given figure = 6cm
Perimeter of the new shape = Length of the side of AB + Length of the side of BC + Length of the side of CD + Length of the side of DE + Length of the side of EF + Length of the side of FG + Length of the side of GH + Length of the side of HA
= 6cm + 18cm + 6cm + 6cm + 6cm + 18cm + 6cm + 6cm
= 24cm + 6cm + 6cm + 6cm + 18cm + 6cm + 6cm
= 30cm + 6cm + 6cm + 18cm + 6cm + 6cm
= 36cm + 6cm + 18cm + 6cm + 6cm
= 42cm + 18cm + 6cm + 6cm
= 60cm + 6cm + 6cm
= 66cm + 6cm
= 72cm.

Question 3.
Label the unknown side lengths. Then, find the perimeter of the shaded rectangle.
$Eureka Math Grade 3 Module 7 Lesson 17 Homework Answer Key h 6$
Answer:
Perimeter of the shaded rectangle = 37in.

Explanation:

$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-17-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 17 Homework Answer Key-3$

Shaded rectangle = BCDG
Length of the side of AB in the given figure = 5in
Length of the side of BC in the given figure = EF – AB = 18in – 5in = 13in
Length of the side of CD in the given figure = FA – DE = 8in – 2in = 6in
Length of the side of DE in the given figure = 2in
Length of the side of EF in the given figure = 18in
Length of the side of FA in the given figure = 8in
Length of the side of GB in the given figure = 6in
Length of the side of GD in the given figure = 13in
Perimeter of the shaded rectangle = Length of the side of BC+ Length of the side of CD + Length of the side of GD + Length of the side of GB
= 13in + 6in + 13in + 6in
= 19in + 13in + 6in
= 31in + 6in
= 37in.

Eureka Math Grade 3 Module 7 Lesson 16 Answer Key

August 12, 2021

Engage NY Eureka Math 3rd Grade Module 7 Lesson 16 Answer Key

Eureka Math Grade 3 Module 7 Lesson 16 Pattern Sheet Answer Key

Multiply.
$Engage NY Math 3rd Grade Module 7 Lesson 16 Pattern Sheet Answer Key p 1$
multiply by 9 (6–10)
Answer:
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-16-Answer-Key$

Explanation:
9 × 5 = 45
9 × 6 = 54
9 × 7 = 63
9 × 8 = 72
9 × 9 = 81
9 × 10 = 90.

Eureka Math Grade 3 Module 7 Lesson 16 Problem Set Answer Key

Question 1.
Find the perimeter of 10 circular objects to the nearest quarter inch using string. Record the name and perimeter of each object in the chart below.

Object	Perimeter (to the nearest quarter inch)
Cap of my jam jar	13$\frac{1}{4}$ inches
Bangle	17$\frac{1}{4}$ inches
Plate of my Dog	34$\frac{1}{4}$ inches
Plastic glass Mouth	21$\frac{3}{4}$ inches
Lid of my Lunch Box	29$\frac{3}{2}$ inches
Ear ring	2$\frac{2}{4}$ inches
Water Bottle cap	7$\frac{2}{4}$ inches
Pencil Mouth	1$\frac{2}{4}$ inches
Pen Cap	3$\frac{1}{4}$ inches
Perfume Bottom surface	12$\frac{3}{4}$ inches

a. Explain the steps you used to find the perimeter of the circular objects in the chart above.

Answer:
Step 1: Took a string and wrapped around the object.
Step 2: Marked the string met.
Step 3: Measured the length of the string.

Explanation:
First I rolled the String around the object. Later, I marked the string met. Afterwards, I took a ruler to measure the length of the string.

b. Could the same process be used to find the perimeter of the shape below? Why or why not?
$Engage NY Math Grade 3 Module 7 Lesson 16 Problem Set Answer Key pr 1$
Answer: Yes, the same steps would be followed to find the perimeter of the given shape because I use the string to find the perimeter.

Explanation:
The same steps would be followed to find the perimeter of the given shape because I use the string to find the perimeter. First I rolled the String around the object. Later, I marked the string met. Afterwards, I took a ruler to measure the length of the string.

Question 2.
Can you find the perimeter of the shape below using just your ruler? Explain your answer.
$Engage NY Math Grade 3 Module 7 Lesson 16 Problem Set Answer Key pr 2$
Answer:
No, I cant find the perimeter of this given shape because it got curve line in it as which a ruler cant measure it.

Explanation:
A tool used to rule straight lines and measure distances is called as ruler.
No, I cant find the perimeter of this given shape because it got curve line in it as a ruler measures only straight lines.

Question 3.
Molly says the perimeter of the shape below is 6 $\frac{1}{4}$ inches. Use your string to check her work. Do you agree with her? Why or why not?
$Engage NY Math Grade 3 Module 7 Lesson 16 Problem Set Answer Key pr 3$
Answer:
No, she is not correct has I have used my string and found the perimeter of the shape as 5 $\frac{3}{4}$ inches.

Explanation:
Molly says the perimeter of the shape below is 6 $\frac{1}{4}$ inches.
No, she is not correct has I have used my string and found the perimeter of the shape as 5 $\frac{3}{4}$ inches.

Question 4.
Is the process you used to find the perimeter of a circular object an efficient method to find the perimeter of a rectangle? Why or why not?
Answer:
No, I don’t think this process to find the perimeter of a circular object an efficient method to find the perimeter of a rectangle, because I can just use a ruler to measure length of the straight lines.

Explanation:
No, I don’t think this process to find the perimeter of a circular object an efficient method to find the perimeter of a rectangle. A ruler is used to find the lengths of the straight lines which help in finding the perimeter of the shape.

Eureka Math Grade 3 Module 7 Lesson 16 Exit Ticket Answer Key

Use your string to the find the perimeter of the shape below to the nearest quarter inch.
$Eureka Math 3rd Grade Module 7 Lesson 16 Exit Ticket Answer Key t 1$
Answer:
The perimeter of this circular shape is 26 3/4 inches.

Explanation:
I used my string to measure this circular shape. The perimeter of this circular shape is 26 3/4 inches.

Eureka Math Grade 3 Module 7 Lesson 16 Homework Answer Key

Question 1.
a. Find the perimeter of 5 circular objects from home to the nearest quarter inch using string. Record the name and perimeter of each object in the chart below.

Object	Perimeter (to the nearest quarter inch)
Example: Peanut Butter Jar Cap	9$\frac{1}{2}$ inches
Cap of my jam jar	13$\frac{1}{4}$ inches
Plate of my Dog	34$\frac{1}{4}$ inches
Lid of my Lunch Box	29$\frac{3}{2}$ inches
Water Bottle cap	7$\frac{2}{4}$ inches
Pen Cap	3$\frac{1}{4}$ inches

b. Explain the steps you used to find the perimeter of the circular objects in the chart above.
Answer:
Well, as previously discussed I have used a string to measure the perimeter of the circular shapes. I wrapped string around the circular bodies and noted the values where they met. Later I have used a ruler to measured the values.

Explanation:
Used string to measure the perimeter of the circular shapes. I wrapped string around the circular bodies and noted the values where they met. Later I have used a ruler to measured the values.

Question 2.
Use your string and ruler to find the perimeter of the two shapes below to the nearest quarter inch.
$Eureka Math Grade 3 Module 7 Lesson 16 Homework Answer Key h 1$
a. Which shape has a greater perimeter?
b. Find the difference between the two perimeters.

Answer:
a. The perimeter of the given shape B is greater by 3inches than The perimeter of the given shape A.
b. The perimeter of the shape B given using string – The perimeter of the shape A given using string
= 17 1/4 inches – 14 1/4 inches
= 3 inches

Explanation:
a. The perimeter of the given shape A using string = 14 1/4 inches.
The perimeter of the given shape B using string = 17 1/4 inches.

b. Difference:
The perimeter of the shape B given using string – The perimeter of the shape A given using string
= 17 1/4 inches – 14 1/4 inches
= 3 inches.

Question 3.
Describe the steps you took to find the perimeter of the objects in Problem 2. Would you use this method to find the perimeter of a square? Explain why or why not.
Answer:
Step 1: Took a string and wrapped around the given shape A.
Step 2: Marked the string met.
Step 3: Measured the length of the string using ruler.
Step 4: Took a string and wrapped around the given shape B.
Step 5: Marked the string met.
Step 6: Measured the length of the string using ruler.

No, I cant use this process of finding perimeter for Square because Square’s perimeter can be found easily using ruler directly. For finding the perimeter of circular shapes we use string n later the ruler.

Explanation:
First I rolled the String around the given shape A. Later, I marked the string met. Afterwards, I took a ruler to measure the length of the string. same I did with the given shape B.

For finding the perimeter of circular shapes we use string n later the ruler, to know their measurement value. Square is a straight line shape, we can use ruler directly to find its perimeter no need of string.

Eureka Math Grade 3 Module 7 Lesson 15 Answer Key

August 12, 2021

Engage NY Eureka Math 3rd Grade Module 7 Lesson 15 Answer Key

Eureka Math Grade 3 Module 7 Lesson 15 Pattern Sheet Answer Key

Multiply.
$Engage NY Math 3rd Grade Module 7 Lesson 15 Pattern Sheet Answer Key p 1$
multiply by 9 (1–5)
Answer:
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-15-Answer-Key-$

Explanation:
9 × 1 = 9
9 × 2 = 18
9 × 3 = 27
9 × 4 = 36
9 × 5 = 45.

Eureka Math Grade 3 Module 7 Lesson 15 Problem Set Answer Key

Question 1.
Mrs. Kozlow put a border around a 5-foot by 6-foot rectangular bulletin board. How many feet of border did Mrs. Kozlow use?
Answer:
Mrs. Kozlow used 22ft of border.

Explanation:
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-15-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 15 Problem Set Answer Key-1$
Length of the side of the rectangular bulletin board = 6ft
Width of the side of the rectangular bulletin board = 5ft
Perimeter of the rectangular bulletin board = 2 (Length + Width)
= 2 ( 6ft + 5ft )
= 2 × 11ft
= 22ft.

Question 2.
Jason built a model of the Pentagon for a social studies project. He made each outside wall 33 centimeters long. What is the perimeter of Jason’s model pentagon?
Answer:
Perimeter of the Jason’s model Pentagon = 165 centimeters.

Explanation:
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-15-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 15 Problem Set Answer Key-2$
Length of the Side of the Jason’s model Pentagon = 33 centimeters
Perimeter of the Jason’s model Pentagon = 5 × Side
= 5 × 33 centimeters
= 165 centimeters.

Question 3.
The Holmes family plants a rectangular 8-yard by 9-yard vegetable garden. How many yards of fencing do they need to put a fence around the garden?
Answer:
Perimeter of the rectangular vegetable garden = 34-yard.

Explanation:
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-15-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 15 Problem Set Answer Key-3$
Length of the rectangular vegetable garden= 9-yard
Width of the rectangular vegetable garden = 8-yard
Perimeter of the rectangular vegetable garden = 2 ( Length + Width )
= 2 (9-yard + 8-yard)
= 2 × 17-yard
= 34-yard.

Question 4.
Marion paints a 5-pointed star on her bedroom wall. Each side of the star is 18 inches long. What is the perimeter of the star?
$Engage NY Math Grade 3 Module 7 Lesson 15 Problem Set Answer Key pr 1$
Answer:
Perimeter of the Star = 180 inches.

Explanation:
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-15-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 15 Problem Set Answer Key-4$
Length of the side of the Star = 18 inches
Number of sides of Star = 10
Perimeter of the Star = 10 × Side
= 10 ×18 inches
=180 inches.

Question 5.
The soccer team jogs around the outside of the soccer field twice to warm up. The rectangular field measures 60 yards by 100 yards. What is the total number of yards the team jogs?
Answer:
The total number of yards the team jogs = 640 yards.

Explanation:
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-15-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 15 Problem Set Answer Key-5$
Length of the rectangular soccer field = 100 yards
Width of the rectangular soccer field = 60 yards
Perimeter of the rectangular soccer field = 2 ( Length + Width )
= 2 ( 100 yards + 60 yards )
= 2 × 160 yards
= 320 yards.
Number of rounds the soccer team jogs around the outside of the soccer field to warm up = twice
The total number of yards the team jogs = 320 yards × 2
= 640 yards.

Question 6.
Troop 516 makes 3 triangular flags to carry at a parade. They sew ribbon around the outside edges of the flags. The flags’ side lengths each measure 24 inches. How many inches of ribbon does the troop use?
Answer:
The troop used 216inches of ribbon.

Explanation:
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-15-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 15 Problem Set Answer Key-6$
Number of triangular flags Troop 516 makes = 3 or Three
Length of the triangular flags Troop 516 makes = 24inches
Perimeter of the triangular flags Troop 516 makes = 3 × Side
= 3 × 24inches
= 72inches.
Perimeter of the 3 triangular flags Troop 516 makes = 3 × 72inches
= 216inches.

Eureka Math Grade 3 Module 7 Lesson 15 Exit Ticket Answer Key

Marlene ropes off a square section of her yard where she plants grass. One side length of the square measures 9 yards. What is the total length of rope Marlene uses?
Answer:
The total length of rope Marlene uses = 36 yards.

Explanation:
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-15-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 15 Exit Ticket Answer Key$
Length of the side of the square = 9 yards.
Perimeter of the square = 4 × Side
= 4 × 9 yards
= 36 yards.

Eureka Math Grade 3 Module 7 Lesson 15 Homework Answer Key

Question 1.
Miguel glues a ribbon border around the edges of a 5-inch by 8-inch picture to create a frame. What is the total length of ribbon Miguel uses?
Answer:
The total length of ribbon Miguel uses = 26-inch.

Explanation:
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-15-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 15 Homework Answer Key-1$
Length of the rectangular picture = 8-inch
Width of the rectangular picture = 5-inch
Perimeter of the rectangular picture = 2 ( Length + Width )
= 2 ( 8-inch + 5-inch )
= 2 × 13-inch
= 26-inch.

Question 2.
A building at Elmira College has a room shaped like a regular octagon. The length of each side of the room is 5 feet. What is the perimeter of this room?
Answer:
The perimeter of this room = 40 feet.

Explanation:
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-15-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 15 Homework Answer Key-2$
length of each side of the regular octagon room = 5 feet
Perimeter of the regular octagon room = 8 × Side
= 8 × 5 feet
= 40 feet.

Question 3.
Manny fences in a rectangular area for his dog to play in the backyard. The area measures 35 yards by 45 yards. What is the total length of fence that Manny uses?
Answer:
The total length of fence that Manny uses = 160 yards.

Explanation:
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-15-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 15 Homework Answer Key-3$
Length of the rectangular fence = 45 yards
Width of the rectangular fence = 35 yards
Perimeter of rectangular fence = 2 ( Length + Width )
= 2 (45 yards + 35 yards )
= 2 × 80 yards
= 160 yards.

Question 4.
Tyler uses 6 craft sticks to make a hexagon. Each craft stick is 6 inches long. What is the perimeter of Tyler’s hexagon?
Answer:
Perimeter of the Tyler’s hexagon = 36 inches.

Explanation:
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-15-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 15 Homework Answer Key-4..$
Length of the side of the Tyler’s hexagon = 6 inches
Perimeter of the Tyler’s hexagon = 6 × Side
= 6 × 6 inches
= 36 inches.

Question 5.
Francis made a rectangular path from her driveway to the porch. The width of the path is 2 feet. The length is 28 feet longer than the width. What is the perimeter of the path?
Answer:
Perimeter of the rectangular path = 60 feet.

Explanation:
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-15-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 15 Homework Answer Key-5$
Length of the rectangular path = 28 feet
Width of the rectangular path = 2 feet
Perimeter of the rectangular path = 2 ( Length + Width )
= 2 ( 28 feet + 2 feet )
= 2 × 30 feet
= 60 feet.

Question 6.
The gym teacher uses tape to mark a 4-square court on the gym floor as shown. The outer square has side lengths of 16 feet. What is the total length of tape the teacher uses to mark Square A?
$Eureka Math Grade 3 Module 7 Lesson 15 Homework Answer Key h 1$
Answer:
Perimeter of the Square court = 64 ft.
The total length of tape the teacher uses to mark Square A = 16 ft.

Explanation:
$Eureka Math Grade 3 Module 7 Lesson 15 Homework Answer Key h 1$
Length of the Square court = 16 ft
Perimeter of the Square court = 4 × Side
= 4 × 16 ft
= 64 ft.
The total length of tape the teacher uses to mark Square A = Perimeter of the Square court ÷ 4
= 64 ft ÷ 4
= 16 ft.

Eureka Math Grade 3 Module 7 Lesson 13 Answer Key

August 12, 2021

Engage NY Eureka Math 3rd Grade Module 7 Lesson 13 Answer Key

Eureka Math Grade 3 Module 7 Lesson 13 Pattern Sheet Answer Key

Multiply.
$Engage NY Math 3rd Grade Module 7 Lesson 13 Pattern Sheet Answer Key p 1$
multiply by 8 (1–5)
Answer:
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-13-Answer-Key-$

Explanation:
8 × 1 = 8
8 × 2 = 16
8 × 3 = 24
8 × 4 = 32
8 × 5 = 40.

Eureka Math Grade 3 Module 7 Lesson 13 Problem Set Answer Key

Question 1.
Find the perimeter of the following shapes.
a.
$Engage NY Math Grade 3 Module 7 Lesson 13 Problem Set Answer Key pr 1$
P = 3 in + 8 in + 3 in + 8 in
= _________ in
Answer:
Perimeter of the ABCD Rectangle = Side + Side + Side + Side
= AB + BC +CD + DA
= 8in + 3in + 8in + 3in
= 22in.

Explanation:
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-13-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 13 Problem Set Answer Key- 1a$

Length of the AB side of the Rectangle = 8in
Length of the BC side of the Rectangle = 3in
Length of the CA side of the Rectangle = 8in
Length of the DA side of the Rectangle = 3in
Perimeter of the ABCD Rectangle = Side + Side + Side + Side
= AB + BC +CD + DA
= 8in + 3in + 8in + 3in
= 11in + 8in + 3in
= 19in + 3in
= 22in.

b.
$Engage NY Math Grade 3 Module 7 Lesson 13 Problem Set Answer Key pr 2$
P = ____ cm + ____ cm + ____ cm + ____ cm
= _________ cm
Answer:
Perimeter of the ABCD Square = Side + Side + Side + Side
= AB + BC +CD + DA
= 4cm + 4cm + 4cm + 4cm
= 16cm.

Explanation:
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-13-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 13 Problem Set Answer Key- 1b$
Length of the AB side of the ABCD Square = 4cm
Length of the BC side of the ABCD Square = 4cm
Length of the CD side of the ABCD Square = 4cm
Length of the DA side of the ABCD Square = 4cm
Perimeter of the ABCD Square = Side + Side + Side + Side
= AB + BC +CD + DA
= 4cm + 4cm + 4cm + 4cm
= 8cm + 4cm + 4cm
= 12cm + 4cm
= 16cm.

c.
$Engage NY Math Grade 3 Module 7 Lesson 13 Problem Set Answer Key pr 3$
P = ____ cm + ____ cm + ____ cm
= _________ cm
Answer:
Perimeter of the ABC Triangle = Side + Side + Side
= AB + BC + CA
= 9cm + 11cm + 6cm
= 26cm.

Explanation:
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-13-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 13 Problem Set Answer Key- 1c$
Length of the AB side of the ABC Triangle = 9cm
Length of the BC side of the ABC Triangle = 11cm
Length of the CA side of the ABC Triangle = 6cm
Perimeter of the ABC Triangle = Side + Side + Side
= AB + BC + CA
= 9cm + 11cm + 6cm
= 20cm + 6cm
= 26cm.

d.
$Engage NY Math Grade 3 Module 7 Lesson 13 Problem Set Answer Key pr 4$
P = ____ m + ____ m + ____ m + ____ m
= _________ m
Answer:
Perimeter of the ABCD Trapezium = Side + Side + Side + Side
= AB + BC + CD + DA
= 15m + 9m + 5m + 7m
= 36m.

Explanation:
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-13-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 13 Problem Set Answer Key- 1d$

Length of the AB side of the ABCD Trapezium = 15cm
Length of the BC side of the ABCD Trapezium = 9cm
Length of the CD side of the ABCD Trapezium = 5cm
Length of the DA side of the ABCD Trapezium = 7cm
Perimeter of the ABCD Trapezium = Side + Side + Side + Side
= AB + BC + CD + DA
= 15m + 9m + 5m + 7m
= 24m + 5m + 7m
= 29m + 7m
= 36m.

e.
$Engage NY Math Grade 3 Module 7 Lesson 13 Problem Set Answer Key pr 5$
P = ____ in + ____ in + ____ in + ____ in + ____ in
= _________ in
Answer:
Perimeter of the ABCDE Pentagon = Side + Side + Side + Side + Side
= AB + BC + CD + DE + EA
= 9in + 2in + 2in + 9in + 3in
= 25in.

Explanation:
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-13-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 13 Problem Set Answer Key- 1e$
Length of the AB side of the ABCDE Pentagon = 9in
Length of the BC side of the ABCDE Pentagon = 2in
Length of the CD side of the ABCDE Pentagon = 2in
Length of the DE side of the ABCDE Pentagon = 9in
Length of the EA side of the ABCDE Pentagon = 3in
Perimeter of the ABCDE Pentagon = Side + Side + Side + Side + Side
= AB + BC + CD + DE + EA
= 9in + 2in + 2in + 9in + 3in
= 11in + 2in + 9in + 3in
= 13in + 9in + 3in
= 22in + 3in
= 25in.

Question 2.
Alan’s rectangular swimming pool is 10 meters long and 16 meters wide. What is the perimeter?
$Engage NY Math Grade 3 Module 7 Lesson 13 Problem Set Answer Key pr 6$
Answer:
Perimeter of the ABCD Rectangle = Side + Side + Side + Side
= AB + BC + CD + DA
= 16m + 10m + 16m + 10m
= 52m.

Explanation:

$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-13-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 13 Problem Set Answer Key- 2$
Length of the AB side of the ABCD Rectangle = 16m
Length of the BC side of the ABCD Rectangle = 10m
Length of the CA side of the ABCD Rectangle = 16m
Length of the DA side of the ABCD Rectangle = 10m
Perimeter of the ABCD Rectangle = Side + Side + Side + Side
= AB + BC + CD + DA
= 16m + 10m + 16m + 10m
= 26m + 16m + 10m
= 42m + 10m
= 52m.

Question 3.
Lila measures each side of the shape below.
$Engage NY Math Grade 3 Module 7 Lesson 13 Problem Set Answer Key pr 7$
a. What is the perimeter of the shape?
b. Lila says the shape is a pentagon. Is she correct? Explain why or why not.
Answer:
a. The perimeter of the ABCDE shape = Side + Side + Side + Side + Side
= AB + BC + CD + DE + EA
= 9in + 6in + 3in + 2in + 4in
= 24in.

b. Lila is correct because Pentagon is a figure which has five sides in it and her figure is a five sided shape.

Explanation:
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-13-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 13 Problem Set Answer Key- 3a$
a. The perimeter of the ABCDE shape = ???
Length of the AB side of the ABCDE shape = 9in
Length of the BC side of the ABCDE shape = 6in
Length of the CD side of the ABCDE shape = 3in
Length of the DE side of the ABCDE shape = 2in
Length of the EA side of the ABCDE shape = 4in
The perimeter of the ABCDE shape = Side + Side + Side + Side + Side
= AB + BC + CD + DE + EA
= 9in + 6in + 3in + 2in + 4in
= 15in + 3in + 2in + 4in
= 18in + 2in + 4in
= 20in + 4in
= 24in.

b. Pentagon is a figure which has five side in it. Lila is correct.

Eureka Math Grade 3 Module 7 Lesson 13 Exit Ticket Answer Key

Which shape below has the greater perimeter? Explain your answer.
$Eureka Math 3rd Grade Module 7 Lesson 13 Exit Ticket Answer Key t 1$
Answer:
Perimeter of shape A = 14in
Perimeter of shape B = 15in
Perimeter of shape B is greater than the Perimeter of shape A because the measurement value of Perimeter of shape B is more than the the measurement value of Perimeter of shape A.

Explanation:
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-13-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 13 Exit Ticket Answer Key$
Perimeter of shape A = Side + Side + Side + Side + Side + Side + Side
= AB + BC + CD + DE + EF + FG + GA
= 2in + 2in + 2in + 2in + 2in + 2in + 2in
= 4in + 2in + 2in + 2in + 2in + 2in
= 6in + 2in + 2in + 2in + 2in
= 8in + 2in + 2in + 2in
= 10in + 2in + 2in
= 12in + 2in
= 14in.
Perimeter of shape B = Side + Side + Side + Side + Side
= HI + IJ + JK + KL +LH
= 4in + 2in + 2in + 4in + 3in
= 6in + 2in + 4in + 3in
= 8in + 4in + 3in
= 12in + 3in
= 15in.

Eureka Math Grade 3 Module 7 Lesson 13 Homework Answer Key

Question 1.
Find the perimeters of the shapes below. Include the units in your equations. Match the letter inside each shape to its perimeter to solve the riddle. The first one has been done for you.
$Eureka Math Grade 3 Module 7 Lesson 13 Homework Answer Key h 1.1$

$Eureka Math Grade 3 Module 7 Lesson 13 Homework Answer Key h 1$
What kind of meals do math teachers eat?
$Eureka Math Grade 3 Module 7 Lesson 13 Homework Answer Key h 2$
Answer:
Perimeter of q Triangle shape = 21in.
Perimeter of r Pentagon shape = 36ft.
Perimeter of s Parallelogram shape = 24cm.
Perimeter of a Trapezium shape = 28yd.
Perimeter of m rhombus shape = 16in.
Perimeter of e Rectangular shape = 26cm.
Perimeter of u quadrilateral shape = 20m.
Perimeter of l Pentagon shape = 15m.

$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-13-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 13 Homework Answer Key-1$
Square meals kind of meals math teachers eats.

Explanation:
$Eureka Math Grade 3 Module 7 Lesson 13 Homework Answer Key h 1.1$
$Eureka Math Grade 3 Module 7 Lesson 13 Homework Answer Key h 1$

Perimeter of q Triangle shape = Side + Side + Side
= 7in + 7in + 7in
= 14in + 7in
= 21in.

Perimeter of r Pentagon shape = Side + Side + Side + Side + Side
= 6ft + 9ft + 6ft + 6ft + 9ft
= 15ft + 6ft + 6ft + 9ft
= 21ft + 6ft + 9ft
= 27ft + 9ft
= 36ft.

Perimeter of s Parallelogram shape = Side + Side + Side + Side
= 7cm + 5cm + 7cm + 5cm
= 12cm + 7cm + 5cm
= 19cm + 5cm
= 24cm.

Perimeter of a Trapezium shape = Side + Side + Side + Side
= 9yd + 7yd + 5yd + 7yd
= 16yd + 5yd + 7yd
= 21yd + 7yd
= 28yd.

Perimeter of m rhombus shape = Side + Side + Side + Side
= 4in + 4in + 4in + 4in
= 8in + 4in + 4in
= 12in + 4in
= 16in.

Perimeter of e Rectangular shape = Side + Side + Side + Side
= 8cm + 5cm + 8cm + 5cm
= 13cm + 8cm + 5cm
= 21cm + 5cm
= 26cm.

Perimeter of u quadrilateral shape = Side + Side + Side + Side
= 6m + 4m + 7m + 3m
= 10m + 7m + 3m
= 17m + 3m
= 20m.

Perimeter of l Pentagon shape= Side + Side + Side + Side + Side
= 4m + 2m + 2m + 4m + 3m
= 6m + 2m + 4m + 3m
= 8m + 4m + 3m
= 12m + 3m
= 15m.

$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-13-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 13 Homework Answer Key-1$

Question 2.
Alicia’s rectangular garden is 33 feet long and 47 feet wide. What is the perimeter of Alicia’s garden?
$Eureka Math Grade 3 Module 7 Lesson 13 Homework Answer Key h 3$
Answer:
Perimeter of Alicia’s rectangular garden = 160ft.

Explanation:
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-13-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 13 Homework Answer Key-2$
Length of the ABCD Alicia’s rectangular garden = 33ft
Width of the ABCD Alicia’s rectangular garden = 47ft
Perimeter of ABCD Alicia’s rectangular garden = 2 (Length + Width)
= 2 ( 33ft + 47ft )
= 2 × 80ft
= 160ft.

Question 3.
Jaque’s measured the side lengths of the shape below.
$Eureka Math Grade 3 Module 7 Lesson 13 Homework Answer Key h 4$
a. Find the perimeter of Jaques’s shape.
b. Jaques says his shape is an octagon. Is he right? Why or why not?
Answer:
a. Perimeter of Jaques’s shape = Side + Side + Side + Side + Side + Side + Side + Side
= AB + BC + CD + DE + EF + FG + GH +HA
= 7 in + 3 in + 4 in+ 5 in + 4 in + 3 in + 2 in +5 in
= 33in.

Explanation:
a.
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-13-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 13 Homework Answer Key-2a$
Perimeter of Jaques’s shape = Side + Side + Side + Side + Side + Side + Side + Side
= AB + BC + CD + DE + EF + FG + GH +HA
= 7 in + 3 in + 4 in+ 5 in + 4 in + 3 in + 2 in +5 in
= 10 in + 4 in + 5 in + 4 in + 3 in + 2 in +5 in
= 14 in + 5 in + 4 in + 3 in + 2 in +5 in
= 19 in + 4 in + 3 in + 2 in +5 in
= 23 in + 3 in + 2 in +5 in
= 26 in + 2 in+5 in
= 28 in + 5 in
= 33 in.

b. Yes, he is correct. Jaques says his shape is an octagon because in geometry , an octagon is an eight-sided polygon or 8-gon. His shape has eight sides.

Explanation:
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-13-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 13 Homework Answer Key-2a$
His shape has eight sides. In geometry , an octagon is an eight-sided polygon or 8-gon.

Eureka Math Grade 3 Module 7 Lesson 12 Answer Key

August 12, 2021

Engage NY Eureka Math 3rd Grade Module 7 Lesson 12 Answer Key

Eureka Math Grade 3 Module 7 Lesson 12 Pattern Sheet Answer Key

Multiply.
$Engage NY Math 3rd Grade Module 7 Lesson 12 Pattern Sheet Answer Key p 1$
multiply by 7 (6–10)
Answer:
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-12-Answer-Key-Eureka Math 3 Module 7 Lesson 12 Pattern Sheet Answer Key$

Explanation:
7 × 6 = 42
7 × 7 = 49
7 × 8 = 56
7 × 9 = 63
7 × 10 = 70.

Eureka Math Grade 3 Module 7 Lesson 12 Problem Set Answer Key

Question 1.
Measure and label the side lengths of the shapes below in centimeters. Then, find the perimeter of each shape.
a.
$Engage NY Math Grade 3 Module 7 Lesson 12 Problem Set Answer Key pr 1$
Perimeter = _____cm +_____cm +_____cm +_____cm
= _______ cm
Answer:
Perimeter of the ABCD given shape = Side + Side + Side + Side
= 2cm + 2cm + 2cm + 2cm
= 8cm.

Explanation:
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-12-Answer-Key-Eureka Math 3 Module 7 Lesson 12 Pattern Sheet Answer Key-1a$
Length of the AB side of the ABCD shape = 2cm
Length of the BC side of the ABCD shape = 2cm
Length of the CD side of the ABCD shape = 2cm
Length of the DA side of the ABCD shape = 2cm
Perimeter of the given ABCD shape = Side + Side + Side + Side
= AB + BC + CD+ DA
= 2cm + 2cm + 2cm + 2cm
= 4cm + 2cm + 2cm
= 6cm + 2cm
= 8cm.

b.
$Engage NY Math Grade 3 Module 7 Lesson 12 Problem Set Answer Key pr 2$
Perimeter = _____________________
= _______ cm
Answer:
Perimeter of the given ABCDEF Hexagon shape = Side + Side + Side + Side + Side + Side
= 3cm + 3cm + 3cm + 3cm + 3cm + 3cm
= 18cm.

Explanation:
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-12-Answer-Key-Eureka Math 3 Module 7 Lesson 12 Pattern Sheet Answer Key-1b$
Length of the AB side of the given ABCDEF Hexagon shape = 3cm.
Length of the BC side of the given ABCDEF Hexagon shape = 3cm.
Length of the CD side of the given ABCDEF Hexagon shape = 3cm.
Length of the DE side of the given ABCDEF Hexagon shape = 3cm.
Length of the EF side of the given ABCDEF Hexagon shape = 3cm.
Length of the FA side of the given ABCDEF Hexagon shape = 3cm.
Perimeter of the given ABCDEF Hexagon shape = Side + Side + Side + Side + Side + Side
= AB + BC + CD + DE + EF + FA
= 3cm + 3cm + 3cm + 3cm + 3cm + 3cm
= 6cm +3cm + 3cm + 3cm + 3cm
= 9cm +3cm + 3cm + 3cm
= 12cm +3cm + 3cm
= 15cm + 3cm
= 18cm.

c.
$Engage NY Math Grade 3 Module 7 Lesson 12 Problem Set Answer Key pr 3$
Perimeter = _____________________
= _______ cm
Answer:
Perimeter of the given ABCD Parallelogram shape = Side + Side + Side + Side
= 4cm + 4cm + 4cm + 4cm
= 16cm.

Explanation:
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-12-Answer-Key-Eureka Math 3 Module 7 Lesson 12 Pattern Sheet Answer Key-1c$
Length of the AB side of the given ABCD Parallelogram shape = 4cm
Length of the BC side of the given ABCD Parallelogram shape = 4cm
Length of the CD side of the given ABCD Parallelogram shape = 4cm
Length of the DA side of the given ABCD Parallelogram shape = 4cm
Perimeter of the given ABCD Parallelogram shape = Side + Side + Side + Side
=AB + BC + CD +DA
= 4cm + 4cm + 4cm + 4cm
= 8cm + 4cm + 4cm
= 12cm + 4cm
=16cm.

d.
$Engage NY Math Grade 3 Module 7 Lesson 12 Problem Set Answer Key pr 4$
Perimeter = _____________________
= _______ cm
Answer:
Perimeter of the ABC Triangle = Side + Side + Side
= 5cm + 5cm + 5cm
= 15cm.

Explanation:
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-12-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 12 Problem Set Answer Key-1d$
Length of the AB side of the ABC Triangle = 5cm
Length of the BC side of the ABC Triangle = 5cm
Length of the CA side of the ABC Triangle = 5cm
Perimeter of the ABC Triangle = Side + Side + Side
= AB + BC + CA
= 5cm + 5cm + 5cm
= 10cm + 5cm
= 15cm.

e.
$Engage NY Math Grade 3 Module 7 Lesson 12 Problem Set Answer Key pr 5$
Perimeter = _____________________
= _______ cm
Answer:
Perimeter of the given ABCDEF figure = Side + Side + Side + Side + Side + Side
= AB + BC + CD + DE+ EF + FA
= 5.5cm+ 1cm + 3cm + 2cm + 3cm + 3cm
= 17.5cm

Explanation:
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-12-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 12 Problem Set Answer Key-1e$
Length of AB side if the given ABCDEF figure = 5.5cm
Length of BC side if the given ABCDEF figure = 1cm
Length of CD side if the given ABCDEF figure = 3cm
Length of DE side if the given ABCDEF figure = 2cm
Length of EF side if the given ABCDEF figure = 3cm
Length of FA side if the given ABCDEF figure = 3cm
Perimeter of the given ABCDEF figure = Side + Side + Side + Side + Side + Side
= AB + BC + CD + DE+ EF + FA
= 5.5cm+ 1cm + 3cm + 2cm + 3cm + 3cm
= 6.5cm + 3cm + 2cm + 3cm + 3cm
= 9.5cm + 2cm + 3cm + 3cm
= 11.5cm + 3cm + 3cm
= 14.5cm + 3cm
= 17.5cm

Question 2.
Carson draws two triangles to create the new shape shown below. Use a ruler to find the side lengths of Carson’s shape in centimeters. Then, find the perimeter.
$Engage NY Math Grade 3 Module 7 Lesson 12 Problem Set Answer Key pr 6$
Answer:
Perimeter of ABCD Carson’s shape = Side + Side + Side + Side
= AB + BC + CD+ DA
= 2cm + 2cm + 2cm + 2cm
=8cm.

Explanation:
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-12-Answer-Key-Eureka Math 3 Module 7 Lesson 12 Pattern Sheet Answer Key-2$

Length of AB side of ABCD Carson’s shape = 2cm
Length of BC side of ABCD Carson’s shape = 2cm
Length of CD side of ABCD Carson’s shape = 2cm
Length of DA side of ABCD Carson’s shape = 2cm
Perimeter of ABCD Carson’s shape = Side + Side + Side + Side
= AB + BC + CD+ DA
= 2cm + 2cm + 2cm + 2cm
=4cm + 2cm + 2cm
= 6cm + 2cm
=8cm.

Question 3.
Hugh and Daisy draw the shapes shown below. Measure and label the side lengths in centimeters. Whose shape has a greater perimeter? How do you know?
$Engage NY Math Grade 3 Module 7 Lesson 12 Problem Set Answer Key pr 7$
Answer:
Perimeter of ABCDE Hugh’s shape = Side + Side + Side + Side + Side
= AB + BC + CD + DE + EA
= 3cm + 3cm + 3cm + 3cm + 3cm
= 15cm.
Perimeter of FGHI Daisy’s shape = Side + Side + Side + Side
= FG+ GH+ HI+ IF
= 4cm + 5cm + 4cm + 3cm
= 16cm.
Perimeter of FGHI Daisy’s shape is greater than the Perimeter of ABCDE Hugh’s shape because the measurement value is greater than the other one’s shape.

Explanation:
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-12-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 12 Homework Answer Key-3..$
Length of the AB side of ABCDE Hugh’s shape = 3cm
Length of the BC side of ABCDE Hugh’s shape = 3cm
Length of the CD side of ABCDE Hugh’s shape = 3cm
Length of the DE side of ABCDE Hugh’s shape = 3cm
Length of the EA side of ABCDE Hugh’s shape = 3cm
Perimeter of ABCDE Hugh’s shape = Side + Side + Side + Side + Side
= AB + BC + CD + DE + EA
= 3cm + 3cm + 3cm + 3cm + 3cm
= 6cm + 3cm + 3cm + 3cm
= 9cm + 3cm + 3cm
= 12cm + 3cm
= 15cm.

Length of the FG side of FGHI Daisy’s shape = 4cm
Length of the GH side of FGHI Daisy’s shape = 5cm
Length of the HI side of FGHI Daisy’s shape = 4cm
Length of the IF side of FGHI Daisy’s shape = 3cm
Perimeter of FGHI Daisy’s shape = Side + Side + Side + Side
= FG+ GH+ HI+ IF
= 4cm + 5cm + 4cm + 3cm
= 9cm + 4cm +3cm
= 13cm + 3cm
= 16cm.

Question 4.
Andrea measures one side length of the square below and says she can find the perimeter with that measurement. Explain Andrea’s thinking. Then, find the perimeter in centimeters.
$Engage NY Math Grade 3 Module 7 Lesson 12 Problem Set Answer Key pr 8$
Answer:
Andrea’s figure is a Square. So, her figure’s all sides are going to be equal. Yes, she is correct in her thinking.
Perimeter of ABCD Andrea’s Square = Side + Side + Side + Side
= 4cm + 4cm + 4cm+ 4cm
= 16cm.

Explanation:
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-12-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 12 Problem Set Answer Key-4$
Andrea’s figure is a Square. So, her figure’s all sides are going to be equal. Yes, she is correct in her thinking, ” measuring one side length of the square below, she can find the perimeter with that measurement.”
Length of AB side of Andrea’s Square = 4cm
Perimeter of ABCD Andrea’s Square = Side + Side + Side + Side
= 4cm + 4cm + 4cm+ 4cm
= 8cm + 4cm + 4cm
=12cm + 4cm
= 16cm.

Eureka Math Grade 3 Module 7 Lesson 12 Exit Ticket Answer Key

Measure and label the side lengths of the shape below in centimeters. Then, find the perimeter.
$Eureka Math 3rd Grade Module 7 Lesson 12 Exit Ticket Answer Key t 1$
Perimeter = __________________________________________
= _______ cm
Answer:
Perimeter of the given ABCDEFGHIJK Shape = Side + Side + Side + Side + Side + Side + Side + Side + Side + Side + Side + Side
= AB + BC+ CD + DE + EF + FG + GH + HI + IJ + JK +KL + LA
= 4cm + 2cm + 2cm + 4cm + 2cm + 2cm + 4cm + 2cm + 2cm + 4cm + 2cm + 2cm
= 32cm.

Explanation:
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-12-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 12 Exit Ticket Answer Key$
Length of the AB side of the given ABCDEFGHIJK Shape = 4cm
Length of the BC side of the given ABCDEFGHIJK Shape = 2cm
Length of the CD side of the given ABCDEFGHIJK Shape = 2cm
Length of the DE side of the given ABCDEFGHIJK Shape = 4cm
Length of the EF side of the given ABCDEFGHIJK Shape = 2cm
Length of the FG side of the given ABCDEFGHIJK Shape = 2cm
Length of the GH side of the given ABCDEFGHIJK Shape = 4cm
Length of the HI side of the given ABCDEFGHIJK Shape = 2cm
Length of the IJ side of the given ABCDEFGHIJK Shape = 2cm
Length of the JK side of the given ABCDEFGHIJK Shape = 4cm
Length of the KL side of the given ABCDEFGHIJK Shape = 2cm
Length of the LA side of the given ABCDEFGHIJK Shape = 2cm
Perimeter of the given ABCDEFGHIJK Shape = Side + Side + Side + Side + Side + Side + Side + Side + Side + Side + Side + Side
= AB + BC+ CD + DE + EF + FG + GH + HI + IJ + JK +KL + LA
= 4cm + 2cm + 2cm + 4cm + 2cm + 2cm + 4cm + 2cm + 2cm + 4cm + 2cm + 2cm
= 6cm + 2cm + 4cm + 2cm + 2cm + 4cm + 2cm + 2cm + 4cm + 2cm + 2cm
= 8cm + 4cm + 2cm + 2cm + 4cm + 2cm + 2cm + 4cm + 2cm + 2cm
= 12cm + 2cm + 2cm + 4cm + 2cm + 2cm + 4cm + 2cm + 2cm
= 14cm + 2cm + 4cm + 2cm + 2cm + 4cm + 2cm + 2cm
= 16cm + 4cm + 2cm + 2cm + 4cm + 2cm + 2cm
= 20 cm + 2cm + 2cm + 4cm + 2cm + 2cm
= 22cm + 2cm + 4cm + 2cm + 2cm
= 24cm + 4cm + 2cm + 2cm
= 28cm + 2cm + 2cm
= 30cm + 2cm
= 32cm.

Eureka Math Grade 3 Module 7 Lesson 12 Homework Answer Key

Question 1.
Measure and label the side lengths of the shapes below in centimeters. Then, find the perimeter of each shape.
a.
$Eureka Math Grade 3 Module 7 Lesson 12 Homework Answer Key h 1$
Perimeter = _____cm +_____cm +_____cm
= _______ cm
Answer:
Perimeter of ABC triangle = Side + Side + Side
= AB + BC + CA
= 3cm + 5cm + 4cm
= 12cm.

Explanation:
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-12-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 12 Homework Answer Key-1a$
Length of the AB side of ABC triangle = 3cm
Length of the BC side of ABC triangle = 5cm
Length of the CA side of ABC triangle = 4cm
Perimeter of ABC triangle = Side + Side + Side
= AB + BC + CA
= 3cm + 5cm + 4cm
= 8cm + 4cm
= 12cm.

b.
$Eureka Math Grade 3 Module 7 Lesson 12 Homework Answer Key h 2$
Perimeter = _____________________
= _______ cm
Answer:
Perimeter of ABCD rectangle = Side + Side + Side + Side
= AB + BC + CD + DA
= 6cm + 4cm + 6cm + 4cm
= 20cm.

Explanation:
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-12-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 12 Homework Answer Key-1b$
Length of the AB side of ABCD rectangle = 6cm
Length of the BC side of ABCD rectangle = 4cm
Length of the CD side of ABCD rectangle = 6cm
Length of the DA side of ABCD rectangle = 4cm
Perimeter of ABCD rectangle = Side + Side + Side + Side
= AB + BC + CD + DA
= 6cm + 4cm + 6cm + 4cm
= 10cm + 6cm + 4cm
= 16cm + 4cm
= 20cm.

c.
$Eureka Math Grade 3 Module 7 Lesson 12 Homework Answer Key h 3$
Perimeter = _____________________
= _______ cm
Answer:
Perimeter of the ABCD Quadrilateral = Side + Side + Side + Side
= AB + BC + CD + DA
= 3cm + 4cm + 5cm + 4cm
= 16cm.

Explanation:
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-12-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 12 Homework Answer Key-1c$
Length of the AB side in the ABCD Quadrilateral = 3cm
Length of the BC side in the ABCD Quadrilateral = 4cm
Length of the CD side in the ABCD Quadrilateral = 5cm
Length of the DA side in the ABCD Quadrilateral = 4cm
Perimeter of the ABCD Quadrilateral = Side + Side + Side + Side
= AB + BC + CD + DA
= 3cm + 4cm + 5cm + 4cm
= 7cm + 5cm + 4cm
= 12cm + 4cm
= 16cm.

d.
$Eureka Math Grade 3 Module 7 Lesson 12 Homework Answer Key h 4$
Perimeter = _____________________
= _______ cm
Answer:
Perimeter of the ABCD Parallelogram = Side + Side + Side + Side
= AB + BC + CD + DA
= 5cm + 5cm + 5cm + 5cm
= 20cm.

Explanation:
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-12-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 12 Homework Answer Key-1d$
Length of the AB side of the ABCD parallelogram = 5cm
Length of the BC side of the ABCD parallelogram = 5cm
Length of the CD side of the ABCD parallelogram = 5cm
Length of the DA side of the ABCD parallelogram = 5cm
Perimeter of the ABCD Parallelogram = Side + Side + Side + Side
= AB + BC + CD + DA
= 5cm + 5cm + 5cm + 5cm
= 10cm + 5cm + 5cm
= 15cm + 5cm
= 20cm.

e.
$Eureka Math Grade 3 Module 7 Lesson 12 Homework Answer Key h 5$
Perimeter = _____________________
= _______ cm
Answer:
Perimeter of the given ABCDEFGH figure = Side + Side + Side + Side + Side + Side + Side + Side
= AB + BC + CD + DE + EF + FG + GH + HA
= 2cm + 2cm + 3.5cm + 2cm + 2cm + 2.5cm + 7.5cm + 2.5cm
= 24cm.

Explanation:
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-12-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 12 Homework Answer Key-1e$
Length of AB side of the given ABCDEFGH figure = 2cm
Length of BC side of the given ABCDEFGH figure = 2cm
Length of CD side of the given ABCDEFGH figure = 3.5cm
Length of DE side of the given ABCDEFGH figure = 2cm
Length of EF side of the given ABCDEFGH figure = 2cm
Length of FG side of the given ABCDEFGH figure = 2.5cm
Length of GH side of the given ABCDEFGH figure = 7.5cm
Length of HA side of the given ABCDEFGH figure = 2.5cm
Perimeter of the given ABCDEFGH figure = Side + Side + Side + Side + Side + Side + Side + Side
= AB + BC + CD + DE + EF + FG + GH + HA
= 2cm + 2cm + 3.5cm + 2cm + 2cm + 2.5cm + 7.5cm + 2.5cm
= 4cm + 3.5cm + 2cm + 2cm + 2.5cm + 7.5cm + 2.5cm
= 7.5cm + 2cm + 2cm + 2.5cm + 7.5cm + 2.5cm
= 9.5cm + 2cm + 2.5cm + 7.5cm + 2.5cm
= 11.5cm + 2.5cm + 7.5cm + 2.5cm
= 14cm + 7.5cm + 2.5cm
= 21.5cm + 2.5cm
= 24cm.

Question 2.
Melinda draws two trapezoids to create the hexagon shown below. Use a ruler to find the side lengths of Melinda’s hexagon in centimeters. Then, find the perimeter.
$Eureka Math Grade 3 Module 7 Lesson 12 Homework Answer Key h 6$
Answer:
Perimeter of ABCDEF Melinda’s hexagon = Side + Side + Side + Side + Side + Side
= AB + BC + CD + DE + EF +FA
= 3cm + 3cm + 3cm + 3cm + 3cm + 3cm
= 18cm.

Explanation:
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-12-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 12 Homework Answer Key-2$
Length of the AB side of ABCDEF Melinda’s hexagon = 3cm
Length of the BC side of ABCDEF Melinda’s hexagon = 3cm
Length of the CD side of ABCDEF Melinda’s hexagon = 3cm
Length of the DE side of ABCDEF Melinda’s hexagon = 3cm
Length of the EF side of ABCDEF Melinda’s hexagon = 3cm
Length of the FA side of ABCDEF Melinda’s hexagon = 3cm
Perimeter of the ABCDEF Melinda’s hexagon = Side + Side + Side + Side + Side + Side
= AB + BC + CD + DE + EF +FA
= 3cm + 3cm + 3cm + 3cm + 3cm + 3cm
= 6cm + 3cm + 3cm + 3cm + 3cm
= 9cm + 3cm + 3cm + 3cm
= 12cm + 3cm + 3cm
= 15cm + 3cm
= 18cm.

Question 3.
Victoria and Eric draw the shapes shown below. Eric says his shape has a greater perimeter because it has more sides than Victoria’s shape. Is Eric right? Explain your answer.
$Eureka Math Grade 3 Module 7 Lesson 12 Homework Answer Key h 7$
Answer:
Yes, Eric is correct because DEFG Square has more sides than the ABC Victoria’s triangle shape.
Perimeter of DEFG Eric’s Square shape is greater than the Perimeter of ABC Victoria’s triangle shape.
Perimeter of ABC Victoria’s triangle shape = 12cm

Explanation:
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-12-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 12 Homework Answer Key-3$
Length of AB Victoria’s triangle shape = 3cm
Length of BC Victoria’s triangle shape = 5cm
Length of CA Victoria’s triangle shape =4cm
Perimeter of ABC Victoria’s triangle shape = Side + Side + Side
= 3cm + 4cm + 5cm
= 7cm + 5cm
= 12cm.

Length of DEFG Eric’s Square shape = 4cm
Perimeter of DEFG Eric’s Square shape = Side × Side
= 4cm × 4cm
= 16cm.
Perimeter of Eric’s Square shape is greater than the Perimeter of Victoria’s triangle shape.

Question 4.
Jamal uses his ruler and a right angle tool to draw the rectangle shown below. He says the perimeter of his rectangle is 32 centimeters. Do you agree with Jamal? Why or why not?
$Eureka Math Grade 3 Module 7 Lesson 12 Homework Answer Key h 8$
Answer:
NO, I disagree with Jamal. Jamal answer is incorrect because actual Perimeter of his ABCD rectangle is 30cm not 32cm.

Explanation:
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-12-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 12 Homework Answer Key-4$
Length of the ABCD Rectangle Jamal drawn = 7.5cm
Width of the ABCD Rectangle Jamal drawn = 4cm
Perimeter of ABCD Rectangle Jamal drawn = Length × Width
= 7.5 × 4
= 30 cm.
Jamal answer is incorrect because actual Perimeter of his ABCD rectangle is 30cm not 32cm.

Eureka Math Grade 3 Module 1 Lesson 5 Answer Key

August 12, 2021

Engage NY Eureka Math 3rd Grade Module 1 Lesson 5 Answer Key

Eureka Math Grade 3 Module 1 Answer Key

Eureka Math Grade 3 Module 1 Lesson 5 Problem Set Answer Key

Question 1.
$Eureka Math Grade 3 Module 1 Lesson 5 Problem Set Answer Key 1$
Divide 6 tomatoes into groups of 3.
There are ____2_____ groups of 3 tomatoes.

Answer:
6 ÷ 3 = 2
There are 2 groups of 3 tomatoes,

Explanation:
Dividing 6 tomatoes into groups of 3 we get
6 ÷ 3 = 2 groups
So there are 2 groups of 3 tomatoes.

Question 2.
$Eureka Math Grade 3 Module 1 Lesson 5 Problem Set Answer Key 2$
Divide 8 lollipops into groups of 2.
There are ____4___ groups.
8 ÷ 2 = ___4____
$Eureka Math Grade 3 Module 1 Lesson 5 Answer Key-1$

Answer:

There are 4 groups,

Explanation:
Dividing 8 lollipops into groups of 2 as
8 ÷ 2 = 4 we get 4 groups,
So, there are 4 groups of 2.

Question 3.
$Eureka Math Grade 3 Module 1 Lesson 5 Problem Set Answer Key 3$
Divide 10 stars into groups of 5.
10 ÷ 5 = ___2____
$Eureka Math Grade 3 Module 1 Lesson 5 Answer Key-2$

Answer:

There are 2 groups,

Explanation:
Dividing 10 stars into groups of 5 as
10 ÷ 5 = 2 we get 2 groups,
So, there are 2 groups of 5.

Question 4.
$Eureka Math Grade 3 Module 1 Lesson 5 Problem Set Answer Key 4$
Divide the shells to show 12 ÷ 3 = ____4____,
where the unknown represents the number of groups.
How many groups are there? ___4_____
$Eureka Math Grade 3 Module 1 Lesson 5 Answer Key-3$

Answer:

There are 4 groups,

Explanation:
Dividing 12 shells into groups of 3 as
12 ÷ 3 = 4 we get 4 groups,
So, there are 4 groups of 3.

Question 5.
Rachel has 9 crackers. She puts 3 crackers in each bag.
Circle the crackers to show Rachel’s bags.
$Eureka Math Grade 3 Module 1 Lesson 5 Problem Set Answer Key 5$
a. Write a division sentence where the answer represents the number of Rachel’s bags.
b. Draw a number bond to represent the problem.
$Eureka Math Grade 3 Module 1 Lesson 5 Answer Key-4$

Answer:

Division sentence 9 ÷ 3 = 3,
Number of Rachel’s bags are 3,

Explanation:
Given Rachel has 9 crackers.
She puts 3 crackers in each bag.
Circled the crackers to show Rachel’s bags,
a. Division sentence 9 ÷ 3 = 3,
therefore, number of Rachel’s bags are 3.
b.
$Eureka Math Grade 3 Module 1 Lesson 5 Answer Key-5$
Explanation:
Drawn a number bond to represent the problem
as shown above

Question 6.
Jameisha has 16 wheels to make toy cars.
She uses 4 wheels for each car.
a. Use a count-by to find the number of cars Jameisha can build. Make a drawing to match your counting.
b. Write a division sentence to represent the problem.

a.
$Eureka Math Grade 3 Module 1 Lesson 5 Answer Key-6$
Answer:
Number of cars Jameisha builds are 4,

Explanation:
Given Jameisha has 16 wheels to make toy cars.
She uses 4 wheels for each car.
Used a count-by to find the number of cars
Jameisha can build as 16 ÷ 4 = 4 cars,
Made a drawing to match my counting as shown above.

b. Division sentence to represent the problem is 16 ÷ 4 = 4 cars,

Explanation:
Given Jameisha has 16 wheels to make toy cars.
She uses 4 wheels for each car, So the division sentence to represent the problem is 16 ÷ 4 = 4 cars.

Eureka Math Grade 3 Module 1 Lesson 5 Exit Ticket Answer Key

Question 1.
Divide 12 triangles into groups of 6.
$Engage NY Math 3rd Grade Module 1 Lesson 5 Exit Ticket Answer Key 6$
12 ÷ 6 = ___2____
$Eureka Math Grade 3 Module 1 Lesson 5 Answer Key-7$
Answer:
There are 2 groups of 6,

Explanation:
Dividing 12 triangles into groups of 6 as 12 ÷ 6 = 2 we get 2 groups,
So, there are 2 groups of 6.

Question 2.
Spencer buys 20 strawberries to make smoothies.
Each smoothie needs 5 strawberries.
Use a count-by to find the number of smoothies
Spencer can make.
Make a drawing to match your counting.

$Eureka Math Grade 3 Module 1 Lesson 5 Answer Key-8$
Answer:
Spencer makes 4 smoothies,

Explanation:
Given Spencer buys 20 strawberries to make smoothies.
Each smoothie needs 5 strawberries.
Used a count-by the number of smoothies
Spencer can make are 20 ÷ 5 = 4,
Made a drawing to match my counting as 5 X 4 = 20 strawberries as shown above in the picture.

Eureka Math Grade 3 Module 1 Lesson 5 Homework Answer Key

Question 1.
$Eureka Math 3rd Grade Module 1 Lesson 5 Homework Answer Key 7$
Divide 4 triangles into groups of 2.
There are _____2____ groups of 2 triangles.
4 ÷ 2 = 2

Answer:
There are 2 groups of 2 triangles,

Explanation:
Dividing 4 triangles into groups of 2 as
4 ÷ 2 = 2 we get 2 groups,
So, there are 2 groups of 2 triangles.

Question 2.
$Eureka Math 3rd Grade Module 1 Lesson 5 Homework Answer Key 8$
Divide 9 eggs into groups of 3.
There are ___3____ groups.
9 ÷ 3 = __3_____
$Eureka Math Grade 3 Module 1 Lesson 5 Answer Key-9$

Answer:
There are 3 groups of 3 eggs,

Explanation:
Dividing 9 eggs into groups of 3 as
9 ÷ 3 = 3 we get 3 groups,
So, there are 3 groups of 3 eggs.

Question 3.
$Eureka Math 3rd Grade Module 1 Lesson 5 Homework Answer Key 9$
Divide 12 buckets of paint into groups of 3.
12 ÷ 3 = __4_____
$Eureka Math Grade 3 Module 1 Lesson 5 Answer Key-10$
Answer:
There are 4 groups of 3 paint buckets,

Explanation:
Divided 12 buckets of paint into groups of 3 as
12 ÷ 3 = 4 we get 4 groups of paint buckets,
So, there are 4 groups of 3 paint buckets.

Question 4.
$Eureka Math 3rd Grade Module 1 Lesson 5 Homework Answer Key 10$
Group the squares to show 15 ÷ 5 = __3___,
where the unknown represents the number of groups.
How many groups are there? ____3____
$Eureka Math Grade 3 Module 1 Lesson 5 Answer Key-11$
Answer:
There are 3 groups of 5 squares,

Explanation:
Grouped the squares to show 15 ÷ 5 = 3,
where the unknown represents the number of groups as 3 groups of 5 squares.

Question 5.
Daniel has 12 apples. He puts 6 apples in each bag.
Circle the apples to find the number of bags Daniel makes.
$Eureka Math 3rd Grade Module 1 Lesson 5 Homework Answer Key 11$
a. Write a division sentence where the answer represents the number of Daniel’s bags.
b. Draw a number bond to represent the problem.
a.
$Eureka Math Grade 3 Module 1 Lesson 5 Answer Key-12$
Daniel’s has 2 bags of 6 apples each,
Division sentence : 12 ÷ 6 = 2 bags,

Explanation:
Daniel has 12 apples and he puts 6 apples in each bag.
Circled the apples to find the number of bags Daniel makes as 12 ÷ 6 = 2 bags,
a. Writing a division sentence where the answer represents the number of Daniel’s bags as 12 ÷ 6 = 2 bags.

b.
$Eureka Math Grade 3 Module 1 Lesson 5 Answer Key-13$
Explanation:
Drawn a number bond to represent the problem as shown above in the picture.

Question 6.
Jacob draws cats. He draws 4 legs on each cat for a total of 24 legs.
a. Use a count-by to find the number of cats Jacob draws. Make a drawing to match your counting.
b. Write a division sentence to represent the problem.

a.
$Eureka Math Grade 3 Module 1 Lesson 5 Answer Key-14$
Answer:
The number of cats Jacob draws are 6,

Explanation:
Given Jacob draws cats. He draws 4 legs on each cat for a total of 24 legs.
a. Used a count-by to find the number of cats Jacob draws as 24 ÷ 4 = 6 cats,
Made a drawing to match my counting as shown above.

b. Division sentence is 24 ÷ 4 = 6 cats,

Explanation:
Wrote a division sentence to represent the problem as
24 ÷ 4 = 6 cats.

Tag: Eureka Math Grade 3 Module 7

Engage NY Eureka Math 3rd Grade Module 7 Lesson 19 Answer Key

Eureka Math Grade 3 Module 7 Lesson 19 Problem Set Answer Key

Eureka Math Grade 3 Module 7 Lesson 19 Exit Ticket Answer Key

Eureka Math Grade 3 Module 7 Lesson 19 Homework Answer Key

Engage NY Eureka Math 3rd Grade Module 7 Lesson 18 Answer Key

Eureka Math Grade 3 Module 7 Lesson 18 Problem Set Answer Key

Eureka Math Grade 3 Module 7 Lesson 18 Exit Ticket Answer Key

Engage NY Eureka Math 3rd Grade Module 7 Mid Module Assessment Answer Key

Eureka Math Grade 3 Module 7 Mid Module Assessment Task Answer Key

Engage NY Eureka Math 3rd Grade Module 7 Lesson 17 Answer Key

Eureka Math Grade 3 Module 7 Lesson 17 Problem Set Answer Key

Eureka Math 3rd Grade Module 7 Lesson 17 Exit Ticket Answer Key

Eureka Math Grade 3 Module 7 Lesson 17 Homework Answer Key

Engage NY Eureka Math 3rd Grade Module 7 Lesson 16 Answer Key

Eureka Math Grade 3 Module 7 Lesson 16 Pattern Sheet Answer Key

Eureka Math Grade 3 Module 7 Lesson 16 Problem Set Answer Key

Eureka Math Grade 3 Module 7 Lesson 16 Exit Ticket Answer Key

Eureka Math Grade 3 Module 7 Lesson 16 Homework Answer Key

Engage NY Eureka Math 3rd Grade Module 7 Lesson 15 Answer Key

Eureka Math Grade 3 Module 7 Lesson 15 Pattern Sheet Answer Key

Eureka Math Grade 3 Module 7 Lesson 15 Problem Set Answer Key

Eureka Math Grade 3 Module 7 Lesson 15 Exit Ticket Answer Key

Eureka Math Grade 3 Module 7 Lesson 15 Homework Answer Key

Engage NY Eureka Math 3rd Grade Module 7 Lesson 13 Answer Key

Eureka Math Grade 3 Module 7 Lesson 13 Pattern Sheet Answer Key

Eureka Math Grade 3 Module 7 Lesson 13 Problem Set Answer Key

Eureka Math Grade 3 Module 7 Lesson 13 Exit Ticket Answer Key

Eureka Math Grade 3 Module 7 Lesson 13 Homework Answer Key

Engage NY Eureka Math 3rd Grade Module 7 Lesson 12 Answer Key

Eureka Math Grade 3 Module 7 Lesson 12 Pattern Sheet Answer Key

Eureka Math Grade 3 Module 7 Lesson 12 Problem Set Answer Key

Eureka Math Grade 3 Module 7 Lesson 12 Exit Ticket Answer Key

Eureka Math Grade 3 Module 7 Lesson 12 Homework Answer Key

Engage NY Eureka Math 3rd Grade Module 1 Lesson 5 Answer Key

Eureka Math Grade 3 Module 1 Lesson 5 Problem Set Answer Key

Eureka Math Grade 3 Module 1 Lesson 5 Exit Ticket Answer Key

Eureka Math Grade 3 Module 1 Lesson 5 Homework Answer Key